基于運動學的高速高精密銑削力建模：綜合模型與試驗

李剛，張宇，李斯，朱錕鵬，*

1．常州先進制造技術研究所，常州 213164

2．中國科學院 合肥物質科學研究院 智能機械研究所 先進制造技術中心，常州 213164

3．武漢科技大學 機械自動化學院，武漢 430081

高速高精密銑削是數控加工技術發展的新階段，具有加工效率高，加工表面質量好以及能耗低等優勢，可滿足航空、航天、精密儀器及醫療器械等行業對精密、復雜零部件的加工需求［1］。相比于常規切削，高速精密銑削時切削力的變化更為復雜。影響高精密銑削加工精度的原因有很多種，比如刀具磨損效應［2-3］、刀具彈性變形效應［4-5］以及刀具尺寸效應［6-7］等。研究高速精密銑削過程中的動態切削力、切削機理以及影響切削力大小的各種因素，對提高零件加工精度和優化加工工藝方法具有重要的理論和實踐意義。對銑削力的精確建模是研究切削機理和加工動力學的基礎。銑削過程中對銑削力的準確預測可以反饋出刀具銑削狀態信息，從而進一步推斷出刀具變形、磨損以及能量損耗等情況［8-9］。目前相關學者已經提出了眾多關于瞬時銑削力的建模方法，主要建模方法包括：經驗法［10］、有限元法［11-12］、解析法及機械法等［13-14］。董永亨等［15］運用齊次坐標變換法建立了球頭銑刀的運動狀態方程并利用改進后的Z-MAP 方法建立了瞬時切削厚度模型。最后，利用微元積分的方法建立了瞬時銑削力模型。Jia 等［16］針對高速銑削過程中難以加工的材料，提出了一種考慮工件材料特性的球頭銑削力預測模型。該模型基于微分和斜切削機理，將金屬切削過程看作是一系列微分斜切削過程的線性疊加。Lu 等［17］研究了鎳基高溫合金銑削過程中切削力變化規律較為復雜的問題，根據切削厚度最小值，基于切削力與切削層面積的比例關系，建立了以剪切效應為主導的切削力預測模型。Wan 等［18］將塑性理論與滑移線場理論相結合，首次推導出材料分離模型。根據建立的分離模型，從理論上推導出最小切削厚度并建立了分別考慮剪切和犁切效應的切削力模型。

高速精密銑削過程中，刀具由于制造或裝配等誤差導致機床主軸回轉中心與實際加工中的刀具回轉中心之間不重合，從而產生刀具跳動。由于刀具跳動的存在將會導致每個切削刃所受到的切削力大小不同而加速刀具磨損，降低加工精度。因此，刀具跳動［19-20］是影響銑削力預測模型精度的重要因素之一。Zhang 等［21］提出了一種考慮刀具跳動的銑削力預測模型方法。基于線性插補的概念，提出了一種計算刀具瞬時切削位置角的新方法。在此基礎上，通過坐標變換建立了考慮刀具跳動的瞬時切削厚度解析模型。Sahoo 等［22］基于解析模型，提出了一種混合方法來預測微銑削力。該混合方法綜合考慮了刀具跳動和最小切削厚度對瞬時切削厚度的影響并利用有限元方法計算切削力系數。最后，提出了一種更加高效的機械銑削力建模方法。Zhang等［23］提出了一種簡單有效的測量刀具跳動參數的方法，該方法以位移測量為基礎，通過求解刀具參數的相關方程，得到刀具跳動長度和跳動角。在分析刀具切削軌跡的基礎上，提出了微銑削單刃切削的判定準則，并通過銑削實驗驗證了單刃切削現象。Zhang 等［24］根據刀具刃口尺寸效應和最小切削厚度，分別建立了由犁耕力和剪切力主導下的銑削力模型。此外，還考慮了刀具加工過程中的軸向偏移，建立了刀具瞬時撓度模型。

另一方面，刀具磨損直接影響著銑削力大小以及刀具變形，最終導致加工誤差的產生［25-26］。Sun 等［27］研究了切削力與刀具側刃磨損之間的關系，建立了考慮刀面磨損的立銑削三維切削力模型。在給定切削條件、刀具幾何形狀以及工件材料的情況下，可方便預測出刀具磨損作用下的切削力大小。Zhou 等［28］通過研究刀具單齒進給量、切削速度和刀具傾角等切削參數對刀具側面磨損的影響，揭示了球頭銑刀銑削時的磨損形式和磨損機理，最后，建立了考慮刀刃側面磨損的微銑削力解析模型。Oliaei 和Karpat［29］分析了刀具磨損對微銑削力和表面粗糙度的影響，識別出有利于微銑削加工的工藝參數。其研究結果可用于微銑削加工工藝參數的選擇和刀具狀態監測系統。岳彩旭等［30］針對銑削拼接模具過程中刀具磨損引起銑削力變化的問題，根據材料硬度的不同，建立了刀具后刀面摩擦應力與后刀面磨損量的函數關系。最后，結合剪切力模型建立了考慮刀具后刀面磨損的銑削力模型。

綜上所述，高速精密銑削過程中， 切削刃將受到周期機械沖擊載荷、刀具磨損、主軸跳動等因素的綜合影響， 其受力狀態變得相當復雜。當高速銑削過程中采用較小的切削進給量時，其加工狀態將類似于微銑削過程，銑削過程中的刀具彈性變形效應也需要考慮到高速銑削力模型中。雖然很多學者已經對銑削力預測模型進行了廣泛的研究和討論，但過去對高速精密銑削力預測模型的研究中，大多數模型僅僅考慮了刀具跳動、彈性變形或者兩種之一對其的影響。然而，高速精密銑削加工過程中的刀具磨損效應以及彈性變形效應是其中不容忽視的因素。刀具磨損不僅會造成銑削刃銑削半徑的變化，而且還會影響刀具跳動、彈性變形的大小。同時刀具跳動、彈性變形的變化會導致刀具每齒磨損程度的不同。這些影響因素相互作用，最終將會嚴重影響銑削力的大小。為準確預測銑削力，其模型應最大限度考慮刀具磨損、刀具跳動、彈性變形等因素對其的影響。本文綜合分析了上述因素對瞬時切削厚度的影響規律，提出了一種綜合切削厚度計算模型。通過分析各因素之間的相互作用對銑削力大小變化的影響，建立了通用性更強、預測準確度更高的銑削力通用模型，最后，通過高速銑削實驗驗證了理論模型的正確性。

1 基于運動學的綜合切削厚度模型

高速銑削過程中，瞬時切削厚度的精確建模是建立切削力模型的基礎。傳統瞬時切削厚度模型的具體表達形式［31］為

式中：h為刀尖上的任意位置角θ處的瞬時切削厚度；fam為每齒進給量；κ為刀具軸線與刀刃上任意一點到球頭連線的軸向沉浸角。

理論的瞬時切削厚度被定義為當前刀尖運動軌跡與之前切削所生成表面之間的最小距離。傳統銑削過程中，通常將之前切削形成的表面與刀尖運動軌跡相吻合，這種認知是一種很好的近似過程。然而，隨著刀具持續的運動過程中，刀尖實際切削運動軌跡與理論切削運動軌跡并不重合，刀具實際切削過程中的磨損效應、彈性變形等都會對先前生成的切削表面產生重大影響。本節基于運動學理論，求解出真實的刀尖運動軌跡，并綜合考慮多種因素對瞬時切削厚度的影響，建立了一種更精確，更符合實際銑削狀態下的瞬時切削厚度模型。

1.1 綜合影響因素建模

1.1.1 刀具跳動模型

高速精密銑削常用于復雜精密構件的加工，銑削中刀具每齒進給量一般都比較小。在實際加工過程中，由于刀具安裝誤差、刀桿制造誤差以及刀具受力變形等都會造成刀具軸線與機床軸線不重合，從而產生刀具跳動。刀具跳動影響著瞬時切削厚度的大小，并決定著工件的加工質量。因此，刀具跳動對切削力模型的影響是一個不容忽略的重要因素之一。

考慮刀具跳動，在刀具上建立如圖1 所示的刀具坐標系XOY，則在刀具位置角θ處所對應的刀刃上任意一點P的運動軌跡表達式［32］為

圖1 刀具跳動示意圖Fig.1 Schematic diagram of tool run-out

式中：vx、vy分別為X、Y軸方向上的進給速度；r0為刀具偏心量；γ為刀具跳動角；ω為刀具旋轉時的角速度；t為切削時間；R為刀具半徑；φk為切削刃k上P點的徑向位置角，其表達式為

式中：ψ為P點在XY平面上的投影線與切削刃在刀尖點的切線之間的夾角；K為刀具切削刃總個數。

1.1.2 刀具磨損模型

高速精密銑削加工中，由于切削速度的提高，刀具磨損的規律具有與常規切削不同的特性，同時刀具磨損對銑削力有顯著的非線性影響。當刀具磨損值累加到一定數量時，會加速刀具與被加工零件之間的摩擦力，從而導致切削力快速增加。因此，精確的銑削力建模過程中，必須把刀具磨損這一重要因素考慮進來，分析與研究其變化規律，從而進一步優化加工工藝，提高加工效率。

銑削加工中，刀具磨損隨時間的增加而不斷增大，其變化規律與所對應的銑削參數有關。根據以往的相關研究，刀具磨損在一定條件下，其磨損量的表達式［33］為

式中：VB 為刀具磨損量；C為與刀具和工件材料的相關參數；n為主軸轉速；v為刀具進給速度；ad為切削深度；D為刀具直徑；k1、k2、k3、k4、k5分別為主軸轉速、進給速度、切削深度、刀具直徑以及切削時間的指數。

球頭銑刀銑削加工時，刀具磨損量與球頭銑刀切削刃所處的微元位置有關，此時球頭銑刀的刀具磨損模型還需要考慮切削刃所處的切削位置，則刀具磨損模型式（4）的表達式變為

式中：VBh為考慮切削刃位置的刀具磨損量，H為球頭銑刀切削微元所處的高度位置；k6為切削微元的指數。

圖2 顯示了球頭銑刀磨損前后切削微元位置的變化情況，球頭銑刀切削微元P點在沒有切削時所對應的軸向位置角為κp，高度為Hp。當經過一段時間切削后，切削微元P點由于球頭部分發生磨損，P點的真實位置變為P0，PP0為刀具磨損部分，此時P0點所對應的位置角為κ1。當刀具沒有發生磨損時，P點所在高度Hp處的銑削徑為Rp，其表達式分別為

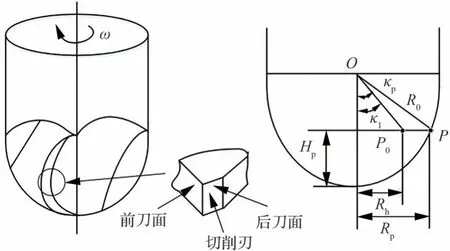
圖2 球頭銑刀磨損示意圖Fig.2 Schematic diagram of ball-end milling cutter wear

式中：R0為球頭銑刀未磨損時的半徑；κp為未發生磨損時的位置角。

當球頭銑刀切削一段時間后，刀具球頭部分將會發生磨損，球頭銑刀在高度Hp處的實際切削點P將變化為點P0，同時高度Hp處所對應的球頭銑刀截面圓上的徑向半徑由原來未磨損時的Rp變化為磨損狀態時的Rh。根據幾何關系，磨損狀態下的徑向半徑Rh的具體表達式為

式中：a2=1/tanκ1。

為簡化推導過程相關公式的表達形式，將式（5）修正為

則由式（7）和式（9）可得

將式（8）代入式（10）可得

通過求解式（11），即可得到球頭銑刀磨損后，在其銑削刃上任意一點P所對應的軸向位置角κ處的徑向切削半徑。

1.1.3 彈性變形模型

常規銑削時，由于切削厚度比較大，刀具刃口半徑與切削厚度相差較大。因此，建立銑削力模型過程中時，通常會忽略刀具刃口半徑的影響。當高速銑削進行精密零部件加工時，刀具每齒進給量較小，切削厚度在10-4mm 和10-2mm 之間，切削厚度與刀具刃口半徑處在同一數量級上，這時加工狀態可以近似看成微細銑削過程，所以需要考慮刀具刃口半徑對銑削力的影響。

當切削厚度比較小時，刀具與工件之間將會出現彈性變形，從而導致瞬時切削厚度與實際切削厚度并不相等。如圖3 所示，刀具切削時刀具彈性變形量為p1，切削時的理論切削厚度為h1，實際切削厚度為h2，則彈性變形與切削厚度之間的表達式［34］為

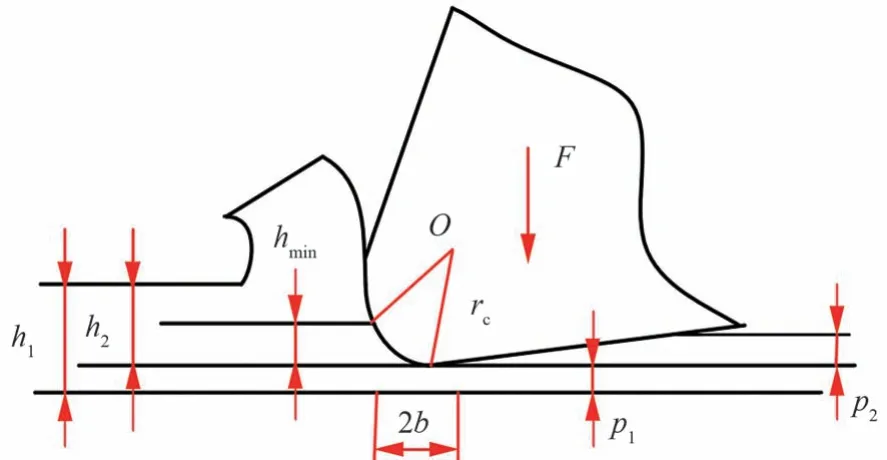
圖3 球頭銑刀切削微元示意圖Fig.3 Schematic diagram of cutter cutting micro element

刀具的實際切削刃口為rc的圓柱面，如圖3 所示，圖中F為刃口作用在被加工工件表面上的力，依據平面和圓柱在彈性接觸時的關系，F可表示為

根據接觸寬度與變形量的幾何形式，p1還可表示為

聯立式（12）和式（14）可得

從式（15）中 可以看出彈性變形與刃口半徑成正比關系，由于E1＞＞E2，則p1最終可表示為

根據對切削刃彈性變形的計算可知，在屈服極限沒有達到時，刀具切削刃與工件材料只發生彈性接觸而不產生切削。而要形成切削，最小切削厚度hmin必須大于切削刃的彈性變形量p1。當切削刃施加在工件材料上的力超過其屈服極限時，工件將發生成塑性變形，從而形成切削。根據材料的最大剪應力可知，最大剪應力應發生在切削合力成45°方向上，即切削刃作用在工件材料上的最大剪應力在θ=45°時發生，此時可得到最小切削厚度hmin=rc(1-cos 45°)≈0.29rc。

1.2 基于運動學的綜合切削厚度模型

球頭銑刀在進行銑削加工時，除了進給方向上有運動，還有自身的回轉運動。根據1.1 節對銑刀加工過程中的刀具跳動、磨損和彈性變形現象的分析，并結合刀具運動情況，建立如圖4 所示的坐標系。在機床床身上建立參考坐標系ORXRYRZR，工件坐標系OW-XWYWZW固定在被加工工件上，刀具坐標系OT-XTYTZT固定在刀具中心上，主軸坐標系OS-XSYSZS固定在主軸上，機床移動軸坐標系為O-XYZ，所建立的各個坐標系方向與參考坐標系方向一致。

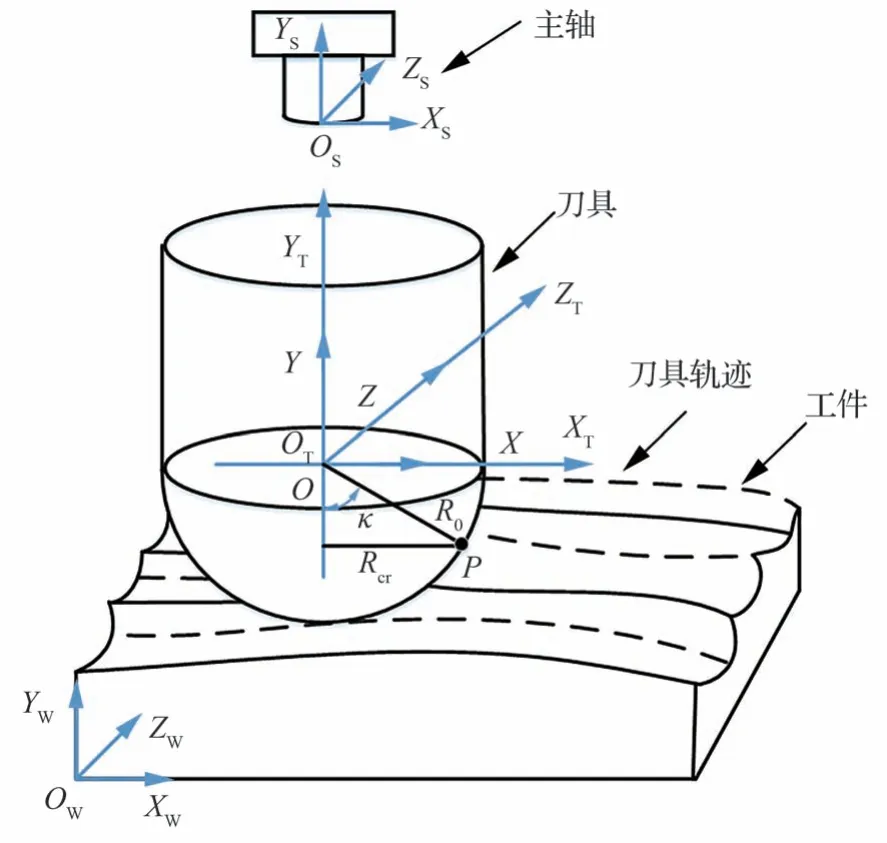
圖4 刀具切削運動坐標系Fig.4 Tool cutting motion coordinate system

當機床靜止時，刀具刀刃上任意一點P在刀具坐標系上的齊次坐標變換矩陣為

式中：Rcr為球頭銑刀切削半徑，當機床運動時，主軸S以及移動軸X、Y、Z在各自坐標系中的變換矩陣T0、TS的表達式分別為

從刀具坐標系OT-XTYTZT變換到工件坐標系OW-XWYWZW的總變換矩陣為

最終可得到刀齒K上任意一點P在工件坐標系OW-XWYWZW內的表達式為

進一步將式（21）整理可得到刀具切削刃上P點在刀具位置角θ處的運動軌跡方程為

刀具銑削加工時，由于受到刀具跳動、磨損以及彈性變形的影響，導致其理論的瞬時切削厚度與實際的瞬時切削厚度不相符。如圖5 所示，藍色實線表示刀具當前第k個切削刃運動軌跡，紅色實線表示刀具前k-（ii=0，1，2，…，k-1）個切削刃運動軌跡，綠色虛線表示刀具切削時受到各種因素影響下，第k-i個切削刃切削時得到的殘余表面，線段MN＇為切削刃在位置角θ處時的實際瞬時切削厚度。求出N＇點的坐標是求出實際瞬時切削厚度的關鍵，點M的坐標可以通過切削刃的運動軌跡方程來確定。點M位于第k個切削刃的運動軌跡上，則在t時刻點M的坐標可表示為

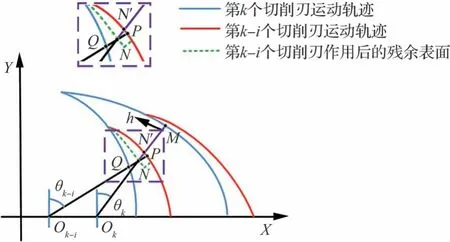
圖5 刀具切削過程示意圖（考慮刀具跳動、磨損和彈性恢復）Fig.5 Schematic diagram of tool cutting process（ considering tool run-out，wear and elastic recovery）

根據1.1.2 節對刀具磨損分析可知，刀具在切削運動時，隨著切削時間的不斷增加，刀具磨損將會出現，并隨著切削時間的增加而變大。因此，考慮刀具磨損時，式（23）中的Rcr等于式（11），則式（23）修正為

由1.1.3 節對刀具彈性變形分析可知，當切削厚度較小時，刀具會發生彈性變形從而導致實際的切削厚度與理論的切削厚度并不相符，此時將刀具彈性變形也同時考慮到切削厚度模型中。如圖5 所示，點N位于第k-i個切削刃作用后的殘余表面上，則點N在tk時刻的坐標為

第k-i條切削刃的接觸點N在t時刻第k條切削刃上的坐標可表示為

聯立式（25）和 式（26）可得

為了簡化計算，設刀具銑削過程中是垂直于工件進行加工，即

式中：θk=ωtk；θk-i=ωtk-i，則式（27）修正為

式中：θk-θk-i=2π/K-μ；φk=φk-i+μ；μ為第k-i條切削刃與第k條切削刃在接觸點N的夾角，通過式（29）計算得到μ的表達式為

將式（30）代入式（29）計算得到綜合因素影響下的瞬時切削厚度h的表達式為

基于上述分析，通過考慮銑削過程中的各種影響因素，建立了球頭銑刀的綜合切削厚度模型，揭示了銑削參數與瞬時切削厚度之間的數學關系。傳統的瞬時切削厚度模型表達過于單一，對于傳統銑削以及表面加工精度要求不高的工件來說，其模型可以滿足，但對精密加工、微小構件加工來說，傳統模型存在一定的局限性，不能夠滿足現代加工要求。本文所建立的瞬時綜合切削厚度模型能夠很好的揭示高速精密銑削加工過程中各種因素對其的影響，從而提高銑削加工精度。

2 球頭銑刀銑削力綜合建模

2.1 銑削力綜合建模

根據瞬時剛度力學模型［35-36］，刀具所受切削力可以表示成切削微元受力之和，如圖6 所示。

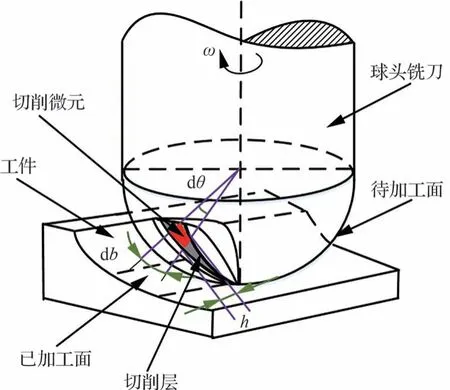
圖6 刀具切削微元Fig.6 Tool cutting micro element

將參與切削的切削刃沿刀軸方向離散成一組非常小的切削微元，此時每個切削微元可以當作正交或者斜角切削過程。切削微元轉過轉角φk時在位置角θk處所受到的切向力dFt、徑向力dFr以及軸向力dFa的表達式［37］為

式中：Kt、Kr、Ka分別為切向、徑向以及軸向銑削力系數；h為瞬時切削厚度；db為切削刃寬度。銑削力系數可以通過實驗數據計算得到，微元切削刃寬度db可表示為

式中：dz為斜角切削微元，即軸向離散高度，式（32）中的微元切削力模型是在切削刃微元的局部坐標系下建立的，而試驗中測得的切削力是在工件坐標系OW-XWYWZW下建立的，所以需要將切削力通過坐標變換到工件坐標系中，則在工件坐標系XYZ方向上的斜角切削微元的切削力分量dFx、dFy、dFz的表達形式為

式中：T為轉換矩陣，其表達式為

將微元切削力沿刀軸方向進行軸向積分，并對每個切削刃上的切削微元進行求和。最后，得到刀具在工件坐標系下3 個方向上的切削力，其表達式為

式中：U0和U1分別表示為積分的下限和上限。

2.2 綜合因素下的切入與切出角

銑削力模型式（36）建立后，需要對銑削過程中的切削刃是否參與切削做出正確判斷，從而得到積分的上下限。判斷切削刃是否參與切削最關鍵的是確認切削刃是否在切入與切出角之間。由于刀具受到螺旋角的影響，瞬時切削厚度沿著切削刃螺旋線逐漸減小或增大，如圖7 所示，滯后角和切削寬度的表達式分別為

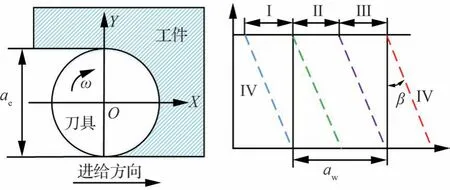
圖7 銑削過程示意圖Fig.7 Schematic diagram of milling process

式中：β為刀具螺旋角；ae為徑向切削寬度。

考慮滯后角的影響，可以定義刀齒在不同階段的切削區域［37］，即切入階段Ι、穩定階段Ⅱ、切出階段Ⅲ以及不切削階段Ⅳ，如圖8 所示。當切削厚度大于最小切削厚度時（h＞hmin），此時會出現相鄰的兩個切削刃處在共同切削狀態，如圖8（a）所示，刀具刀齒從開始切削到完全退出切削時的銑削范圍為［0 π+δ］。當刀齒1 還沒有完全退出切削時，刀齒2 已經開始進入切削并產生切屑，此時會出現共同切削區域，即圖8（a）中的陰影區域，共同切削的范圍在［π π+δ］之間，并給出相應的積分上下限［U0U1］的值，如表1所示。

表1 不同切削區域的積分上下限Table 1 Integration limits in different cutting zones

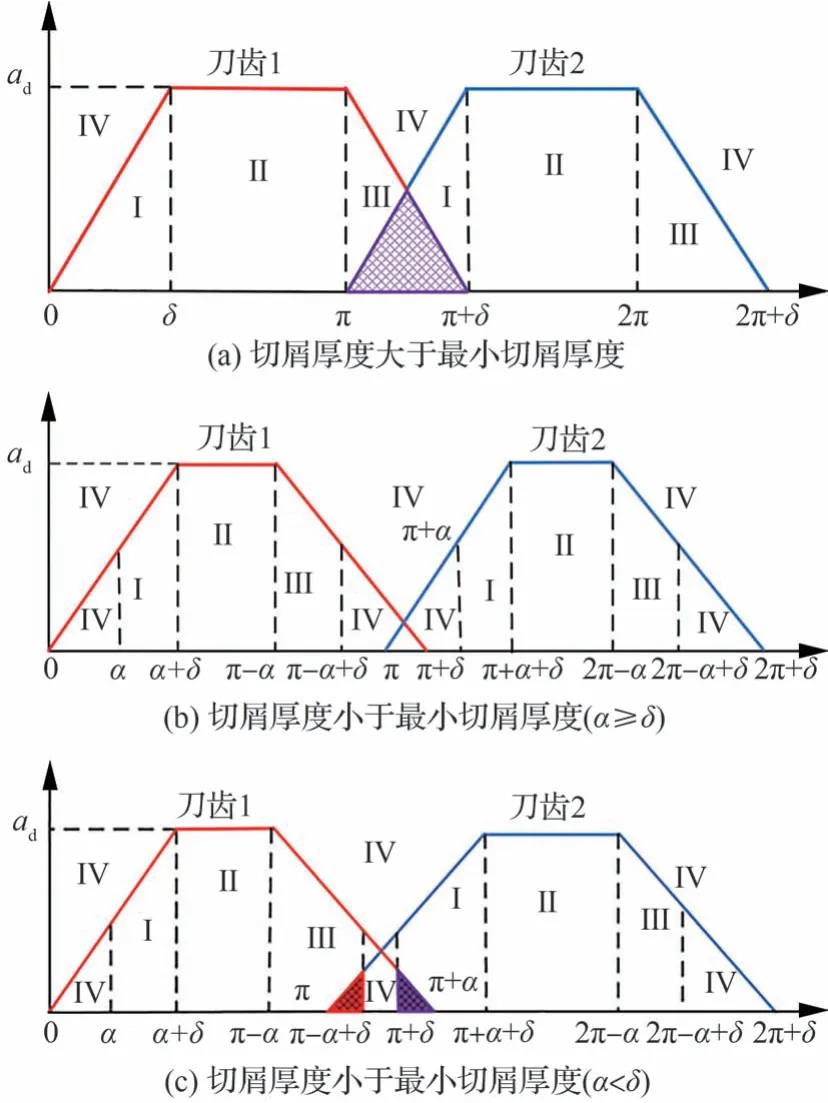
圖8 銑削切入和切出角范圍Fig.8 Range of entry and exit angles

當切削厚度小于最小切削厚度時（h＜hmin），刀具發生彈性變形時所對應的位置角為α，此時切削過程將分為兩種情況，如圖8（b）和8（c）所示。從圖中可以看出刀具實際切削范圍變小了，刀齒1 在［0α］、［π π+δ］范圍內，將不會產生切削，一個周期內的刀齒切削范圍變為［απ-α+δ］。當刀具發生彈性變形時所對應的位置角α大于刀具滯后角δ時，此時會出現相鄰的兩個切削刃將不存在共同切削產生切屑的狀態，如圖8（b）所示，其相交部分在不產生切削階段的Ⅳ之間。當刀具發生彈性變形時所對應的位置角為α小于刀具滯后角δ時，如圖8（c）所示，此時相鄰的兩個切削刃也不存在共同切削產生切屑的狀態，相比圖8（b），其存在3 個相交部分。當刀齒1 還在切削（Ⅲ段）時，刀齒2 進入切削階段但不發生切屑，其相交的陰影區域如圖8（c）紅色部分所示，其相交部分區域為［π π-α+δ］。當刀齒2 開始產生切屑時，刀齒1雖然沒有完全退出切削階段，但此時刀齒1 將不產生切屑，其相交的陰影區域如圖8（c）紫色部分所示，其相交部分區域為［π+απ+δ］。當刀齒1 與刀齒2 相交部分區域為［π-α+δπ+α］時，刀齒1 與刀齒2 都不在切削范圍內，并給出相應的積分限［U0U1］的值，如表1 所示。

3 實驗驗證

3.1 實驗準備

為了驗證所提出的綜合模型的準確性與有效性，在高速加工中心上，如圖9 所示，進行銑削實驗。工件材料為鎳基高溫合金Inconel718，尺寸為112.5 mm×40 mm×78 mm。該材料在高溫環境下具有良好的物理性能，如強度高，應用于航空航天、生物醫學和電子器件等領域。但它存在切削力大、切削溫度高、高速銑削時刀具易磨損等問題。刀具選用3 刃球頭硬質合金端銑刀，直徑為5 mm，刃口圓弧半徑為5 μm。實驗所用的銑刀均選用同一批次生產的以減少由于刀具性能而引起的誤差。實驗過程中銑削力的測量選用Kistler9119 測力儀，采樣頻率為50 kHz，刀具跳動選用千分表進行測量。將刀具安裝在機床主軸上，主軸旋轉360°后，千分表上轉過的數值即為刀具跳動值。為確定刀具跳動長度初始值，使用千分表測量3 次并取平均值為6.5 μm。

圖9 高速銑削工藝實驗裝置Fig.9 Experimental setup of high-speed milling process

工件放置在加工中心平臺上，一共設計10 組實驗，每組實驗的切削深度、每齒進給量等銑削參數如表2 所示。每組實驗銑槽加工300 次，每10 次分為1 組共30 組。為了獲得最佳的銑削力和刀具磨損值，根據以往的研究經驗，選擇每組銑削結束前0.02 s 內的銑削力測量數據作為研究對象。刀具磨損選擇每次銑槽結束后所測量得到的磨損值，每組實驗共測量300 次不同時間段的刀具磨損值，同樣每10 次再分為1 組共分成30 組，為了消除試驗過程中的不確定性，每組實驗重復3 次。基于上述實驗設計，進行銑削實驗，進而分析刀具跳動、磨損等因素對銑削力的影響規律。

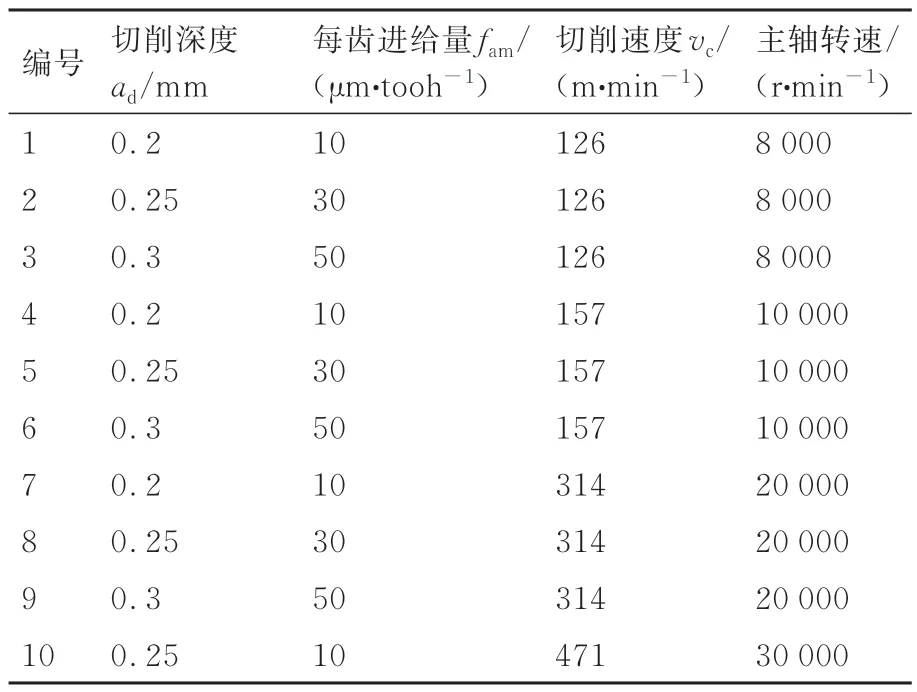
表2 銑削實驗工況Table 2 Machining conditions of milling experiments

3.2 銑削力模型驗證

根據表2 的銑削參數進行銑削實驗并依次測量刀具銑削過程中的磨損值。依據2.2 節中建立的綜合銑削力預測模型，分別計算出每組實驗的理論銑削力值。為了驗證所提出的綜合銑削力預測模型的準確性，選擇第4 組實驗的第1 次銑槽和第5 次銑槽時所測量得到的銑削力值作為比較。根據式（36）計算出一個周期內的理論銑削力波形以及通過銑削實驗測量得到實際銑削力波形，其結果如圖10 所示。通過銑削力預測模型計算得到的理論銑削力在1 個周期內出現3 個峰值，分別對應刀具3 個切削刃銑槽的時間，3 個峰值所對應的最大切削力都不相同，呈現高低波動。隨著銑削實驗的持續進行，第1 次銑槽所得到的銑削力明顯小于第5 次銑槽時的銑削力。這是由于刀具跳動和磨損等因素的存在，改變了傳統刀具每齒瞬時切削厚度形式，從而使刀具每齒所受到的切削力不再相同，同時隨著銑削次數的增加，銑削力也不斷增大。

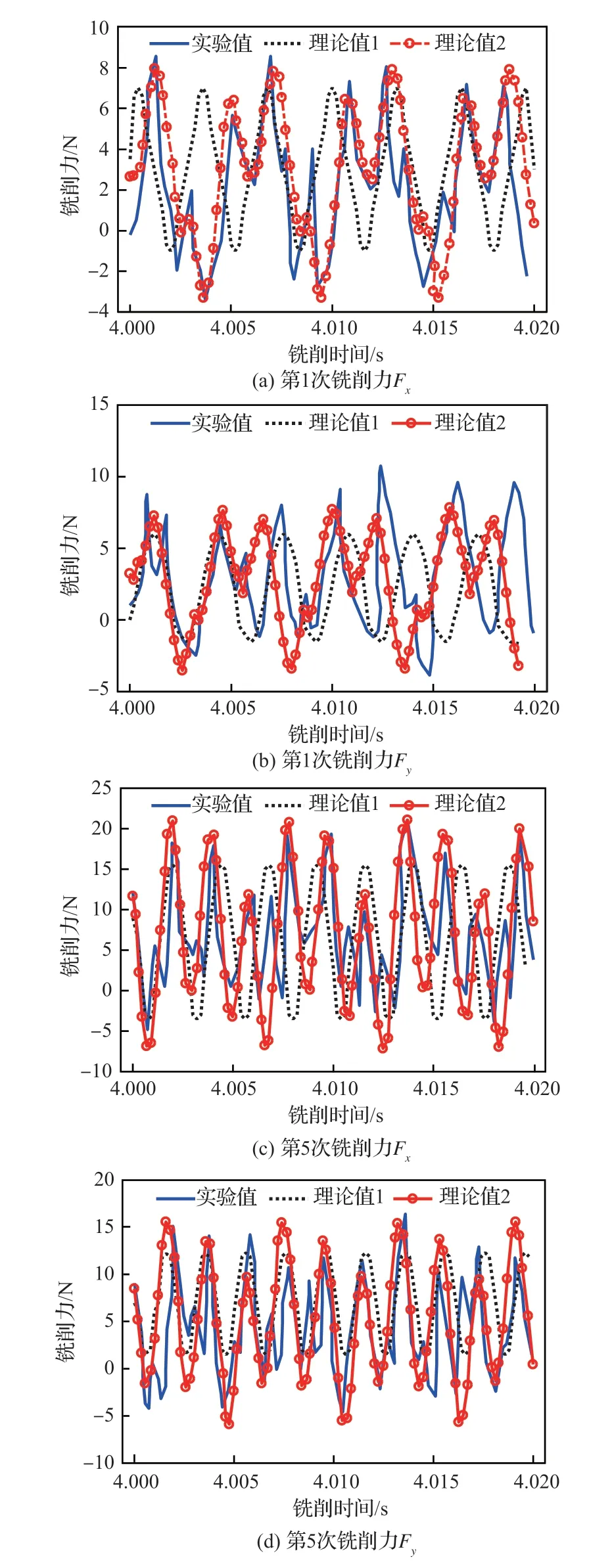
圖10 第4 組銑削力的實驗值與理論值對比Fig.10 Comparison of experimental and theoretical values of milling force in the fourth experiment

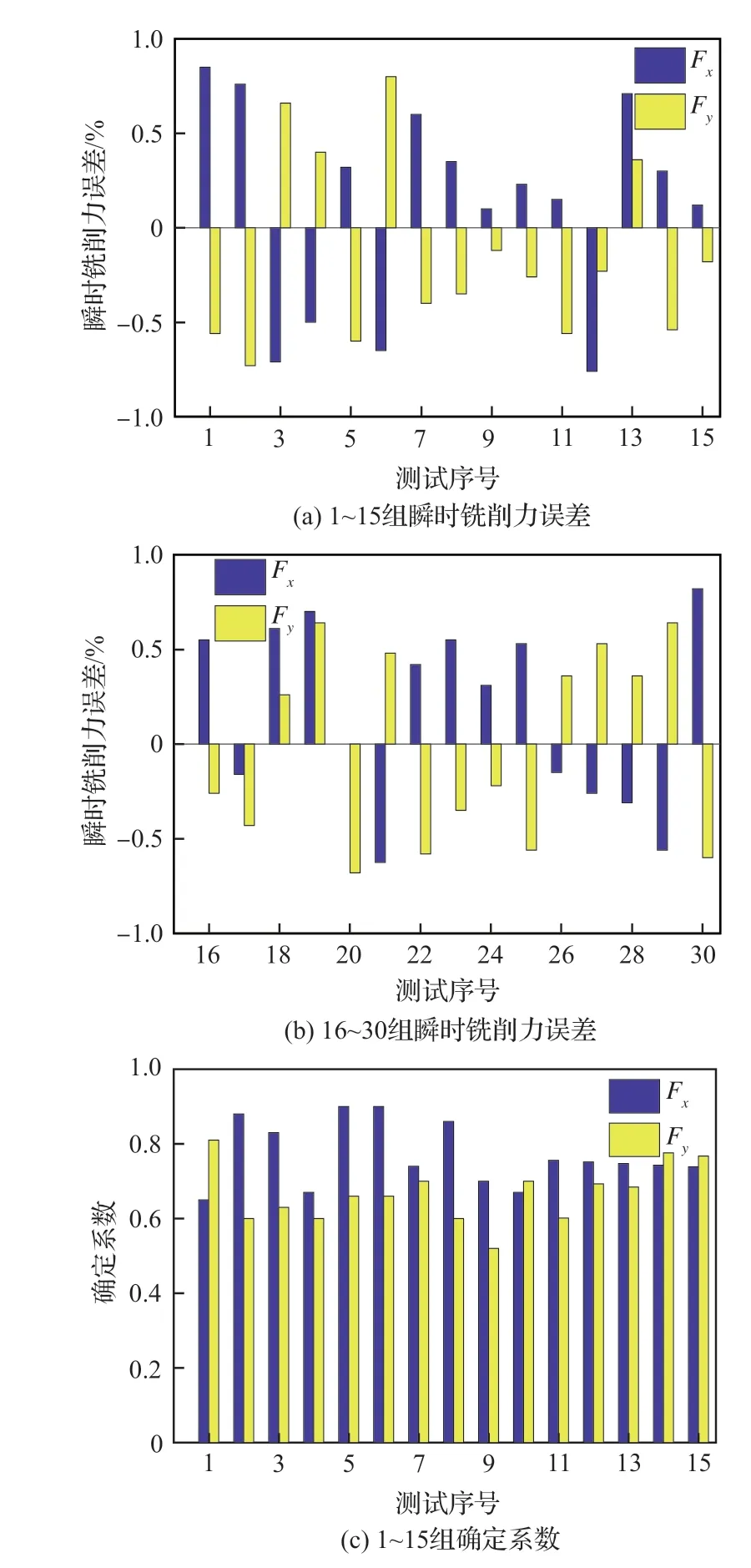
圖10 中黑色虛線段表示的是未考慮刀具跳動和磨損等綜合影響因素下的理論銑削力波形，與圖中藍色線段表示的實際銑削力波形相比，其峰值小于實驗值，總體波形與實驗波形相比還存在一定的偏差。圖10 中紅色線段表示的是考慮刀具跳動和磨損等綜合影響因素下的理論銑削力波形，與圖中實驗銑削力波形相比，其峰值更加接近于實驗值，總體波形與實驗銑削力波形相比偏差較小，與未考慮刀具跳動和磨損等綜合影響因素下的理論銑削力波形相比，其吻合度較高。因此，將刀具跳動、磨損等因素考慮到銑削力模型中，對提高其預測精度具有重要的理論意義。

圖11 所示為根據式（36）所計算得到的理論銑削力與實驗測量所得到的銑削力之間的誤差與確定系數柱狀圖。理論與實驗銑削力之間的誤差ξ可以通過（F1-F2）/F1計算出來，其中F1為理論值，F2為實驗值，從圖11（a）和11（b）中可以看出，1～30 組實驗與理論計算得出的銑削力誤差絕對值全部小于1%。圖11（c）和11（d）為銑削力模型的確定系數R2，R2的值越接近1，則精度越高。除了第9組Fy的R2值小于0.6外，其余Fx和Fy的R2值均大于0.6。這可能是由于機床顫振和加工環境等因素導致的誤差。通過對銑削力的誤差與確定系數分析，結果表明本文所建立的銑削力綜合模型較為精確。

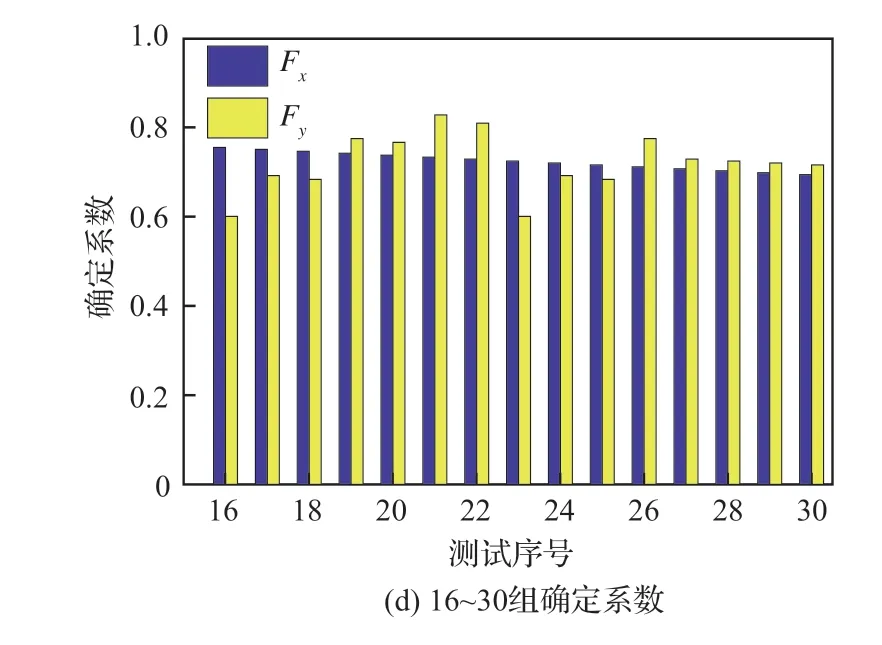
圖11 理論和實驗銑削力之間的誤差與確定系數分析Fig.11 Analysis of error and determination coefficient between theoretical and experimental milling force

3.3 刀具磨損與銑削力的關系

刀具磨損隨銑削時間不斷變化，同時刀具瞬時銑削力也相應發生改變，如圖12 所示。根據式（5）預測出刀具磨損值，如圖12（a）所示，刀具最后一次銑削所產生的磨損值約是第一次銑削時的2.5 倍。刀具在X、Y方向上最后一次銑削時的最大銑削力約是第一次銑削時的5 倍，如圖12（b）和12（c）所示，這表明刀具磨損與瞬時銑削力之間相互影響與關聯，刀具磨損與銑削長度近似成正比關系。因此，可以通過瞬時銑削力的變化特征來監測刀具磨損狀況，從而提高加工精度。根據圖12（a）～12（c），得到刀具在X、Y方向上的最大銑削力與刀具磨損的比值η，如圖12（d）所示，結果表明刀具磨損對X方向上力的影響大于Y方向，即刀具磨損對進給方向上力的影響較大。

圖12 刀具磨損對銑削力的影響Fig.12 Tool wear influence on milling force

為進一步研究瞬時銑削力的變化特征對刀具平均磨損的相關關系，根據銑削實驗分別獲得X、Y、Z軸方向上的瞬時銑削力，利用Budak 等［38］提出的快速標定銑削力系數算法，計算得到3 個方向上的銑削力系數Kt、Kr、Ka。銑削力系數在X、Y、Z軸上的絕對值隨銑削時間的增加而增大。

圖13 顯示了不同時刻的刀具平均磨損值以及所對應的銑削力系數值，從圖中可以看出，隨著刀具平均磨損值的增大，在X軸和Y軸上的銑削力系數Kt、Kr的變化幅度明顯小于Z軸的銑削力系數Ka，Z軸上銑削力系數分別是其他兩個軸的2.5 倍和5.9 倍。

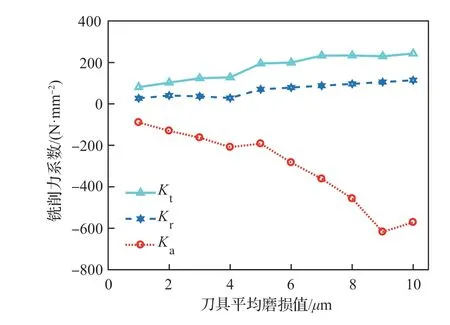
圖13 切削力系數隨刀具平均磨損值的變化Fig.13 Variation of cutting force coefficient with average tool wear

選取第3～7 組實驗數據，基于相關分析，計算得到5 組銑削力系數與刀具平均磨損值的相關系數ρ，如圖14 所示。根據相關性定義，相關系數ρ的絕對值在 0.8～1 之間是極度相關，從圖14 可以看出，銑削力系數與刀具在X軸、Y軸和Z軸上平均磨損值的相關系數ρ均大于0.8，且Z軸上的相關系數ρ約為0.94，5 組Ka的相關系數值均大于其它兩軸的相關系數值。

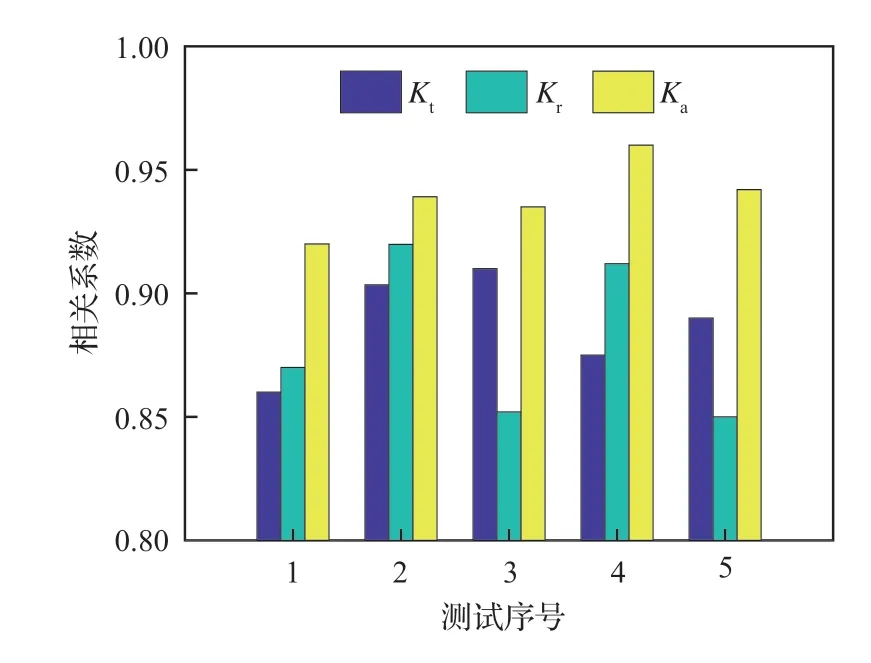
圖14 刀具平均磨損與切削力系數的相關性分析Fig.14 Correlation analysis of average tool wear and cutting force coefficient

根據實驗值計算得到的相關系數ρ為樣本的相關系數，它是總體中的總體相關系數ρτ的估計值。樣本相關系數ρ是否來自ρτ≠0 的總體，還需要對樣本相關系數ρ進行顯著性檢驗。如表3所示，顯著水平τ=0.01 與τ=0.05 時，查表可知，其相關系數臨界值分別為ρ0.05=0.632 與ρ0.05=0.765。由于實驗所列出的5 組相關系數值都大于其臨界值，表中所對應的雙邊顯著性水平的ρ值低于1%，這表明銑削力系數與刀具平均磨損值極其顯著相關。通過研究瞬時銑削力與刀具平均磨損值之間的關系，可以發現瞬時銑削力的動力學特性，特別是Z軸上的銑削力系數較敏感的反映了刀具平均磨損值的進展情況。

表3 相關系數分析Table 3 Correlation coefficient analysis

4 結 論

1）建立了綜合考慮刀具跳動、磨損以及彈性變形的高速精密銑削力模型。該模型可適用于不同的銑削類型，通用性強。刀具彈性變形受到單齒進給量的影響，單齒進給量越小，彈性變形越明顯。同時由于受到刀具沖擊的影響，刀具每齒的磨損程度也不相同。

2）改進的瞬時切削厚度模型能較好地反映切削機理和刀具磨損狀況。預測銑削力與實測銑削力的最大誤差范圍在1%以內，確定系數大于0.6，表明所建立的綜合銑削力模型精確度較高。

3）通過分析刀具磨損與銑削力之間的關系，結果表明，進給方向上的銑削力以及Z向銑削力系數對刀具磨損的影響大于其它兩個軸，因此，刀具切向力以及Z向的銑削力系數的變化特征可以很好的表征刀具磨損的進展狀況，從而優化銑削參數，提高銑削加工精度和效率。