熱顫振地面模擬試驗技術

陳浩宇，王彬文，宋巧治，李曉東

中國飛機強度研究所 航空聲學與振動航空科技重點實驗室，西安 710065

高超聲速飛行器機動性高、航程遠、毀傷能力出色，具有重要的戰略意義與極高的軍事價值，是當前各國研究的熱點。由于飛行馬赫數較高，高超聲速飛行器在飛行過程中除了氣動載荷外還會承受嚴酷的氣動熱載荷，熱載荷與氣動力、結構彈性力、慣性力相互耦合作用，進而引發熱顫振問題。

作為高超聲速飛行器面臨的一種典型氣動彈性問題，熱顫振對飛行器的飛行安全具有重要影響，近年來國內外均對此開展了廣泛的研究。在理論分析方面，研究人員在早期單向熱耦合假設的基礎上進一步研究了熱顫振雙向耦合分析方法，如Culler 和Mcnamara［1］通過簡支平板算例證明了在大約束力條件下雙向耦合計算模型的優勢，楊超等［2］通過壁板顫振分析對比了不同耦合模型在計算結構溫度分布及顫振邊界時的精度差異。此外隨著計算機技術的發展，計算流體力學方法也被逐步應用于熱顫振分析中，如Lamorte 和Friedmann［3］采用徑向基函數將湍流模型引入熱顫振求解器，探究了考慮湍流效應對熱顫振分析結果的影響。在試驗驗證方面，能夠滿足熱顫振研究需求的主要手段為超聲速風洞試驗技術，但該技術實施難度較大，目前相關研究較少，且仍處于方法探索層面，如季辰等［4］采用加熱氣流對翼板結構開展的高超聲速熱顫振風洞試驗研究。

綜上，雖然針對熱顫振理論分析方法的研究已取得諸多進展，但由于理論分析中難以準確考量真實結構存在的非線性、阻尼特性等因素，計算結果的可信度難以保證，因此后續的試驗驗證對于熱顫振研究而言具有重要意義。然而，目前由于高超聲速飛行器熱顫振風洞試驗實施困難、溫度分布與實際存在較大差異等問題，研究人員尚未建立一種能夠滿足型號驗證需求的熱顫振試驗驗證手段，這給高超聲速飛行器研制工作造成了一定阻礙，因此亟需一種在工程層面上可行的試驗驗證技術，彌補當前熱顫振研究方法的不足。

飛行器地面顫振模擬試驗技術是一項采用真實結構作為試驗對象的半實物仿真驗證技術，能夠有效規避顫振理論分析中無法考慮結構非線性、阻尼特性的問題，對理論分析結果能起到很好的補充驗證作用［5］。該技術理念最早由Kearns［6］在1962 年提出，潘樹祥和齊丕騫［7］在20 世紀80 年代即對熱顫振地面模擬試驗技術進行了初步探索。隨著計算機技術及控制技術的發展，在21 世紀初俄羅斯的Smyslov 等［8-9］及美國的Zeng 等［10］先后提出了較為完整的地面顫振模擬試驗方案并進行了試驗驗證。近年來國內也針對該項技術開展技術攻關，如許云濤等［11］對非定常氣動力模擬方法開展了研究，Wang 和Fan［12］提出了基于計算流體力學（Computational Fluid Dynamics，CFD）降階模型的非定常氣動力模擬方法；在試驗系統控制方面，吳志剛等［13-14］分別采用PI 控制器及前置反饋補償方法針對導彈及平板翼面設計了試驗系統控制器，宋巧治等［15-16］則采用魯棒控制算法設計試驗系統控制器，并采用風洞機翼模型進行了試驗驗證。

由于地面顫振模擬試驗技術以地面振動試驗（GVT）系統為基礎，具有較強開放性，因此本文通過在現有試驗系統基礎上增加熱試驗設備模擬氣動熱效應，實現熱環境下結構的顫振測試，從而將常溫顫振地面模擬試驗技術推廣至熱顫振研究領域［17］。由于氣動加熱效應，結構的固有特性及顫振特性會發生變化，因此熱顫振系統具有顯著的時變特性［18］，傳統的針對時不變系統的氣動力模型和顫振邊界測試方法不再適用。為此，本文將對引入時變溫度場的地面顫振模擬試驗技術開展研究，并進一步完成地面熱顫振模擬試驗系統集成與驗證，論證該項技術的可行性。

1 地面顫振模擬試驗原理

飛行器地面顫振模擬試驗技術的核心思想是采用激振設備模擬結構在飛行過程中承受的非定常氣動力，進而達到顫振邊界測試的目的。在試驗過程中，系統通過傳感器測量結構的振動響應信號，將其代入預先獲得的非定常氣動力降階模型從而得到結構應承受的等效氣動力，然后采用激振器將等效氣動力實時加載到結構上，并通過控制算法確保氣動力的精確加載。最終通過對試驗結構施加初始擾動并觀察其響應，實現對真實結構顫振邊界的測試，試驗系統如圖1所示。

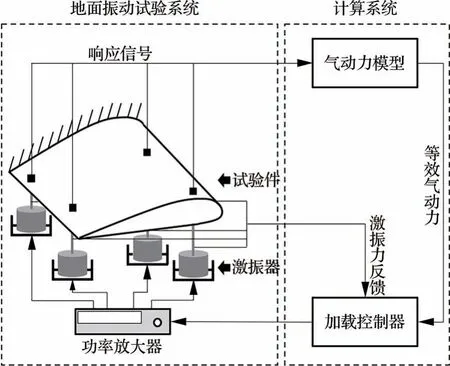
圖1 地面顫振模擬試驗系統Fig.1 Ground flutter simulation test system

2 研究對象

2.1 試驗件

試驗件選擇為如圖2 所示的切尖三角形翼面結構，其根弦長1 800 mm，梢弦長150 mm，半展長1 200 mm，前緣線與根弦的夾角為31°，厚度9 mm，通過螺栓與鋼梁底座連接模擬根部固支邊界。

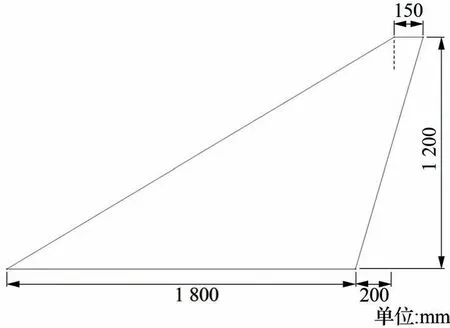
圖2 翼面幾何尺寸Fig.2 Geometrical size of the wing

試驗件材料選為TA15 鈦合金，其密度為4 450 kg/m3，泊松比為0.39。由于本文需要考慮溫度對結構動力學特性的影響，因此表1 給出了部分TA15 材料參數隨溫度變化的數據。

表1 TA15 材料參數Table 1 Material parameters of TA15

2.2 氣動加熱環境分析

實際的高超聲速飛行器飛行軌跡較為復雜，本文為了簡化問題，將飛行環境設定為海拔高度21 km，并以3.8Ma（Ma為馬赫數）速度飛行。

采用FLUENT 和NASTRAN 進行氣動加熱及傳熱計算。采用松耦合的方式進行分析，獲得結構在上述飛行狀態下的穩態溫度場如圖3 所示，其中最高溫約為490 ℃，最低溫約為160 ℃。為了便于試驗開展，設定結構初始均勻溫度場為50 ℃，時變歷程中結構各溫區溫度勻速上升，溫升時長為110 s。

圖3 結構穩態溫度場Fig.3 Steady temperature field of structure

2.3 模態及顫振特性分析

針對上述時變溫度環境下的結構，本節分析工作采用時間凍結假設，在2.2 節設定的溫度時變歷程中均勻采樣，選取12 個工況點進行熱模態數值計算。計算從溫度對材料彈性模量的影響以及不均勻溫度場造成的結構熱應力2 方面考慮了溫度對結構模態特性的影響，相關計算參數已在表1 中給出。結果顯示，在初始溫度場下結構主要參與顫振的第1、2 階模態頻率分別為7.5 Hz與24.1 Hz，而在最終穩態溫度場下這2 階模態頻率分別降至5.4 Hz 與14.5 Hz。結構在這2 種不同溫度場下的第1、2 階模態振型如圖4 所示。

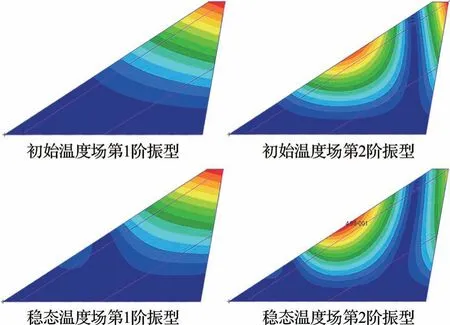
圖4 結構前2 階熱模態振型Fig.4 The first 2 mode shapes of structure

根據上述不同工況點下的熱模態數據開展顫振分析，獲得12 個工況點的第2 階模態分支速度-重力加速度（v-g）曲線如圖5 所示。結果顯示，在翼面結構由初始溫度場升至穩態溫度場的過程中，其顫振臨界速度由2 776 m/s 降至1 221 m/s，顫振頻率由19.7 Hz 降至11.1 Hz。

圖5 第2 階模態v-g 曲線Fig.5 v-g plot of the 2nd mode

3 非定常氣動力模擬

在地面顫振模擬試驗中，需要根據結構響應實時計算非定常氣動力并施加給結構，因此非定常氣動力的計算精度對試驗結果影響顯著。同時由于熱顫振系統中結構的時變特性影響，原有非定常氣動力模擬方法難以滿足試驗需求，因此需要研究可用于時變溫度場試驗系統的非定常氣動力模擬方法。

3.1 考慮多工況的氣動力等效插值點優化

由于設備尺寸等條件的限制，試驗首先要對氣動力模型進行降階處理，從而實現通過少數插值點準確模擬分布非定常氣動力的目標。此類氣動力插值點優化問題的本質是一個離散點的最優化選取問題，對此目前相關研究中通常采用基于廣義力等效的遺傳算法進行優化求解。

廣義力等效優化方法的基本思想是尋找一個插值點布置方案，使得采用該方案時，插值點處的廣義力與熱顫振發生時結構承受的廣義氣動力誤差最小，即此時在插值點處施加的集中力與結構實際承受的分布式非定常氣動力在顫振分析中可視為等價關系。文獻［11］經過推導得，該目標等效于通過優化所得插值點表示的氣動網格插值振型與氣動網格原始振型之間的偏差最小，考慮到各階模態對顫振的貢獻度差異，優化目標可表示為

式中：ηj為j階模態對顫振的貢獻量；NM為主要模態數量；NA為氣動網格結點數量；φij與φij＇分別為縮減前后的氣動力插值振型。obj 越小，說明縮減前后插值振型更接近，氣動力模擬精度更高。

上述基于廣義力等效的優化算法從顫振發生原理的角度出發設定優化目標，在地面顫振模擬試驗方案設計中通常能夠獲得較為可靠的激振點/拾振點優化結果。但由式（1）可以看出，該優化方法采用的縮聚前氣動力插值目標振型是固定的，即該優化結果僅是當前模態振型下的最優插值點，而在時變溫度場中，結構的熱模態振型也會隨時間發生改變，這會導致不同時間節點下的最優插值點有所不同，而試驗過程中激振點/拾振點位置不能改變，因此需要對現有函數進行調整。

對于受氣動加熱影響的結構而言，其溫度場分布形式相對固定，因此在發生熱屈曲前結構隨溫度變化的熱模態振型不會突變，即在結構溫度場單調遞增（或單調遞減）的過程中，結構模態振型中振幅較大區域的移動趨勢基本保持不變。綜上，可以選取結構溫度變化曲線中的極值點作為典型工況點，例如對于本文中溫度單調遞增的試驗系統而言，即為工況1（初始溫度場）與工況12（穩態溫度場）。考慮所有典型工況點的熱模態振型進行加權綜合優化，在式（1）的基礎上構建目標函數如下

式中：NC為選取的典型工況數量。如上文所述，當某組插值點對于2 個相鄰的典型工況為綜合最優方案時，則該組插值點即為這2 個典型工況點之間所有工況點的綜合最優方案。因此，當某組插值點為所有典型工況的綜合最優方案時（即obj最小時），該組插值點即為受熱結構在整個時變過程中的最優激振點/拾振點布置方案。

3.2 基于Kriging 模型的非定常氣動力建模

在采用3.1 節所述方法獲得激振點/拾振點布置方案后，即可將經計算所得作用于激振點處的集中力fs在顫振模擬中等效替代結構實際承受的分布式非定常氣動力，而該模擬氣動力fs可通過式（3）求解

式中：q∞為來流動壓；k=ωb/V為減縮頻率，b為參考長度，ω為正弦振動頻率，V為來流速度；zs為拾振點位移。Gf與Gz分別為描述節點氣動力與位移縮聚關系的插值矩陣，對于本文所采用的翼面結構而言可以通過無限平板樣條（Infinite Plate Splines， IPS）理論［19］獲得。A(k)為氣動力影響系數（Aerodynamic Influence Coefficient，AIC）矩陣，對于超聲速顫振問題可以采用超聲速偶極子格網法［20］獲得，(k)為經過縮聚插值矩陣處理后的降階氣動力影響系數矩陣。

通常，氣動力影響系數矩陣是在頻域建立的，為了使半實物仿真試驗能夠實現，需要將頻域氣動力影響系數矩陣(k)轉換到時域，為此采用最小狀態法對其進行有理函數擬合，可得

將式（4）代入式（3）并做拉氏反變換，即可得到可用于試驗的時域氣動力模型如下

式中：s為拉普斯算子；R為氣動力滯后根對角陣；A0、A1、A2、D、E均為采用最小狀態法得到的系數矩陣。

在熱顫振系統中，由于氣動熱效應會改變結構的模態特性，式（3）中描述拾振點位移與氣動力縮聚關系的插值矩陣Gf、Gz不再是固定值，進而使降階后的AIC 矩陣(k)發生變化，最終導致通過有理函數擬合所得的系數矩陣不再是固定值。從提升試驗精度的角度出發，系統在試驗進程的每一個時間步長都應采用式（3）～式（5）求解一次當前時間節點下的相關矩陣參數，從而建立適用于時變溫度場中結構的非定常氣動力模型，但這種方法顯然無法滿足地面顫振模擬試驗對氣動力計算效率的要求。為了兼顧氣動力模型的計算精度與效率，本文引入Kriging 代理模型構建此類非定常氣動力模型［21］。

Kriging 代理模型是一種基于隨機過程的均方誤差最小的無偏估計模型。以式（5）中任一時變系數矩陣元素Aij(t)為例，在任意時刻t，其對應的值被隨機函數(t)代替，Aij(t)只是該隨機函數可能的結果之一，即

式中：fn(t)為基函數；βn為每個基函數的系數；Z(t)是均值為0，方差為的靜態隨機過程。

將建模所采用的n個樣本點定義為

則采樣時間點之外的模型輸出值可由樣本點數值線性加權得到

其中：ct為加權函數向量，考慮Kriging 模型無偏估計且均方誤差最小的要求，構建ct的求解方程如下

式（8）即為采用Kriging 模型表示的任意時刻的氣動力影響系數矩陣參數，此時式（3）～式（5）的求解過程被簡化為數個低階矩陣計算，能夠滿足試驗對時變系數矩陣計算效率的要求。

3.3 時變顫振邊界跟蹤測試方法

在時不變系統地面顫振試驗中，通過不斷調整氣動力模型中的風速參數，觀測不同風速下的系統響應，即可確定結構的顫振臨界速度，但在熱顫振研究中結構的顫振臨界速度具有時變特性，上述采用固定風速值進行試驗的顫振邊界獲取方法將不再適用。為此，本研究將PID（Proportion Integration Differentiation）控制器引入試驗系統，提出一種顫振邊界實時跟蹤方法，以滿足熱顫振地面模擬試驗的需求。

在試驗中人為調整風速參數尋找被測結構顫振邊界的邏輯可以概括為：結構響應發散則降低風速，結構響應收斂則增高風速。如果將結構響應幅值變化趨勢定義為λ（λ＞0 為響應發散，λ＜0 為響應收斂），則顯然速度修正量ΔV應與λ保持負相關關系，本節所述顫振邊界實時跟蹤方法即希望通過PID 控制器實現上述參數修正過程，而其中最關鍵的工作是將結構響應幅值變化趨勢進行量化，以便PID 控制器識別。

地面顫振模擬試驗中結構的響應信號可近似看作幅值持續變化的正弦信號，可表示為A(t)sinωt。為獲取響應幅值變化趨勢，首先應獲得振動響應的幅值信號A(t)，對原信號做幅值采樣所選取的時間點應滿足式（10）

此時采樣獲得的信號為反映響應信號幅值的階躍信號，但該信號由于噪聲等擾動因素并非單調變化。為了增加控制系統的穩定性，需要排除此類信號局部擾動，使控制器在最大程度上關注幅值整體變化趨勢，為此采用滑動平均法對信號做平滑處理，如式（11）所示

至此已將結構響應信號A(t)sinωt轉化為描述結構響應幅值整體變化趨勢的連續信號(t)如圖6 所示。考慮到實際試驗中的信號質量，直接對(t)作微分處理獲取幅值變化趨勢信號λ(t)會降低系統穩定性，此處設定一個較小的時間間隔Δt，將λ(t)描述為

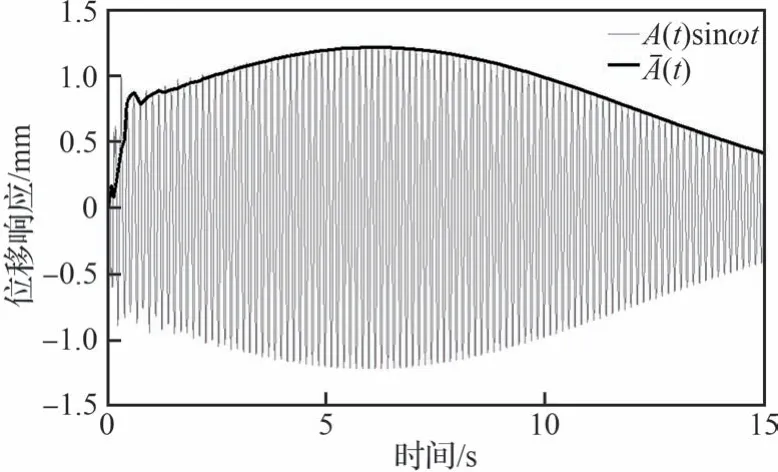
圖6 響應信號幅值Fig.6 Amplitude of response signal

式（12）所獲得的λ(t)即可定量描述結構響應幅值的變化趨勢，在試驗系統構建中即可將其作為PID 控制器的參考信號，通過在前期仿真及預試驗中根據系統響應對控制器參數進行調整，即可實現熱顫振地面模擬試驗中的顫振臨界速度實時跟蹤。

3.4 仿真驗證

本節采用第2 節所述翼面結構顫振系統作為仿真算例，驗證上述針對時變熱顫振系統的非定常氣動力模擬方法。

首先對翼面結構進行激振點/拾振點優化，為便于計算及后續試驗開展，此處設定激振點與拾振點共點。由于本算例中溫度場變化趨勢是持續升高，因此如3.1 節所述選取工況1 與工況12 作為典型工況采用式（2）進行考慮模態振型加權的插值點優化，得到最優插值點位置如圖7所示。

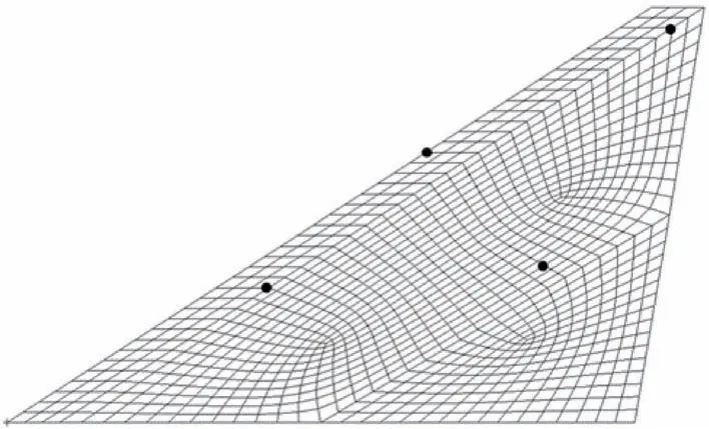
圖7 考慮模態振型加權方法下的最優位置Fig.7 Optimal locations by weighting of modal shape

為了對比優化效果，額外選取工況1、工況7與工況12 分別采用式（1）所示廣義力等效方法進行單工況優化。將4 組優化結果分別代入12 個工況，計算插值點縮減前后插值振型的差異度評價值如圖8 所示。從全工況差異度的角度出發，選用工況1 與工況12 的單工況點優化效果比較差，只能保證選取的參考工況臨近的工況點插值振型差異度較低；選用工況7 的單工況點優化效果與綜合優化效果接近，在工況6～8 下其差異度還低于綜合優化結果，這一現象也符合3.1 節的分析：在升溫過程中結構模態振型中振幅較大區域的移動趨勢基本不變，因此處于時變過程中間位置的工況7 最優節點組合更容易滿足其他工況點插值振型低差異度的要求，但是考慮整個時變過程后顯然采用模態振型加權優化方法能獲得最優結果。

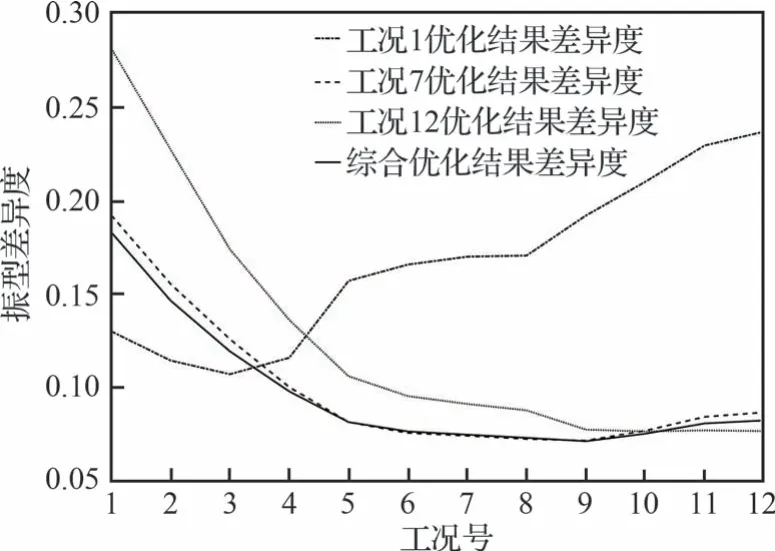
圖8 不同節點組合下的振型差異度Fig.8 Diversity factors of different locations

根據3.2 節及3.3 節所述方法建立非定常氣動力計算模塊，并采用狀態空間表示法建立結構響應計算模塊，組成地面顫振模擬試驗仿真平臺如圖9 所示［22］。

仿真時段與第2 節設定保持一致，總時間歷程為110 s，速度跟蹤模塊在仿真開始后5 s 接入系統，其初始輸出值設定為2 400 m/s。仿真所得速度跟蹤曲線如圖10 所示，其中三角形標記為數值計算所得該時刻采樣工況點的顫振臨界速度。將速度跟蹤曲線穩定后各個工況點處的數值計算結果與仿真結果進行對比，可得仿真誤差最大不超過4%，說明本文提出的非定常氣動力模型及顫振速度跟蹤方法能夠有效應對熱顫振系統的時變特性，可以用于熱顫振地面模擬試驗中。

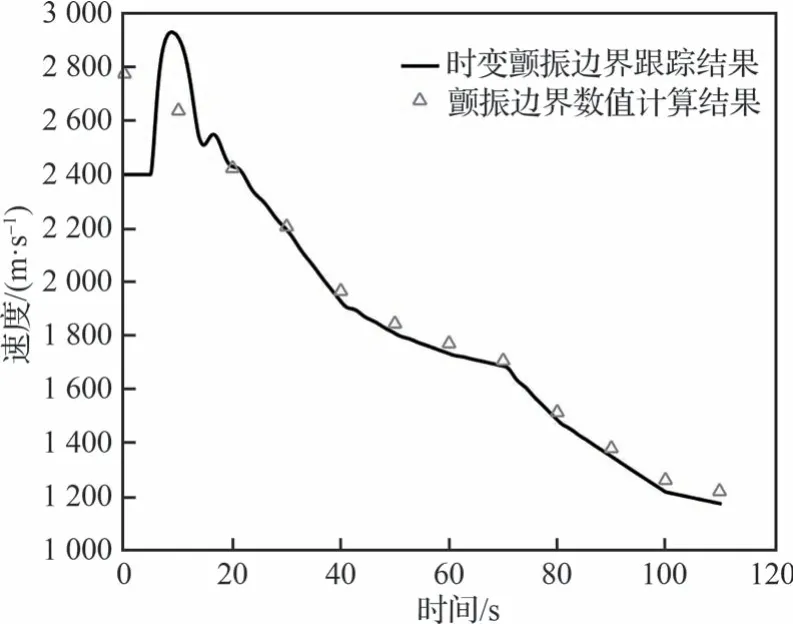
圖10 仿真所得速度跟蹤曲線Fig.10 Velocity tracing result obtained with simulation

4 試驗系統

4.1 氣動熱環境模擬

試驗采用石英燈輻射加熱方式模擬結構承受的具有時變特性的氣動熱環境，加熱系統由石英燈管輻射加熱器、熱電偶、加溫控制儀、可控硅等組成，如圖11 所示。加熱系統工作原理可概括為：系統通過布置于被測結構表面的溫度傳感器獲取測點溫度，加溫控制儀根據測得溫度與預設溫度計算加載修正量并通過可控硅調整石英燈加熱器功率，實現溫度場的閉環控制。

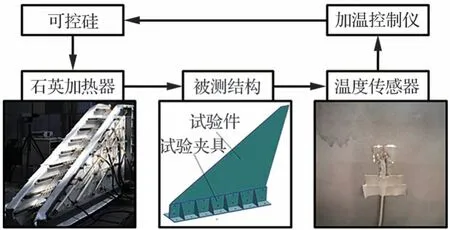
圖11 氣動熱環境模擬系統Fig.11 Aerodynamic heating simulation system

由于結構承受的氣動加熱溫度場具有大梯度分布的特征，因此在綜合考慮試驗設備能力后，將翼面劃分為8 個加熱溫區1～8，翼面兩側溫區對稱布置，加熱方案如圖12 所示。根據試驗設定的溫度邊界條件，加熱方案為先將結構整體預熱至50 ℃，加熱時間為110 s，其中1/5 與2/6 溫區為一組，并始終保持同溫，溫升速率均為4 ℃/s，3/7 溫區溫升速率為2 ℃/s，4/8 溫區溫升速率為1 ℃/s，最終達到翼板沿弦向分布的3 組溫區的溫度分別為490 ℃、270 ℃與160 ℃。

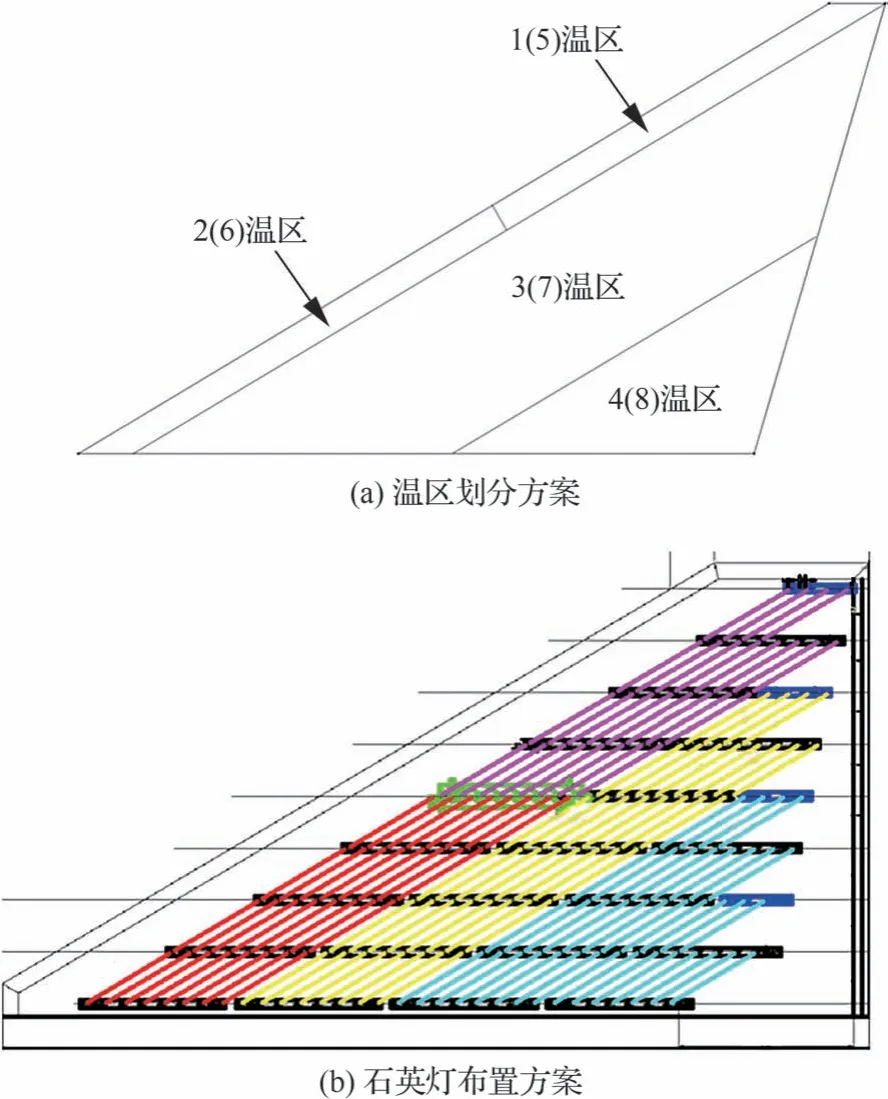
圖12 試驗結構加熱方案Fig.12 Heating scheme for test structure

為評估上述加熱方案所得結構實際溫度場與數值計算所采用溫度場的一致性，采用該加熱方案開展熱模態試驗，并將試驗測得前3 階模態頻率與2.3 節數值計算模態頻率對比如圖13 所示，可知各階模態頻率一致性較好，誤差最大不超過7%，說明該氣動熱環境模擬方案的精度能夠滿足后續試驗需求。

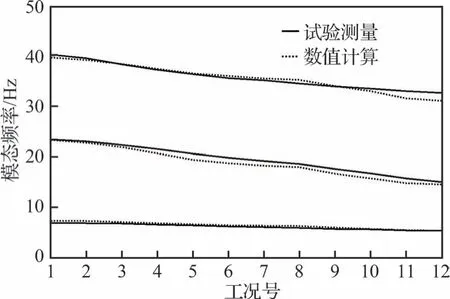
圖13 熱模態試驗數據與數值計算結果Fig.13 Thermal modals test data and numerical results

4.2 響應信號測量

熱顫振地面模擬試驗需要在試驗進程中同時獲得測點的位移、速度、加速度信號，此時如果采用不受高溫環境影響的激光測振儀作為唯一的信號采集設備［23］，就需要把測得的速度信號做積分處理以獲得位移信號，微分處理以獲得加速度信號，而在實際試驗中由于高溫場中熱輻射光、煙霧以及氣體受熱密度變化導致光的折射等影響，激光測振儀信噪比較差，此種處理方法會造成位移信號出現顯著零飄，加速度信號擾動較大，難以滿足數據計算需求。

為了獲得滿足試驗需求的高質量結構響應信號，本文參考吳大方等［24］在超高溫熱模態試驗技術研究中的方法，選用外徑5 mm 內徑3.8 mm 的95%氧化鋁空心陶瓷桿將結構響應信號引出高溫環境，材料密度為3.75 g/cm3。陶瓷桿底部采用螺接的方式固定于結構測點處，如圖14 所示。由于陶瓷桿頂部處于常溫環境，因此可以布置常規加速度傳感器及激光位移傳感器測量響應信號。

圖14 試驗測點構造Fig.14 Test measuring-point construction

雖然文獻［24］已經證明由于陶瓷桿剛度大密度小，其引入的附加質量對結構模態特性的影響不大，但地面顫振試驗關注的是結構的振動響應，因此還需要對陶瓷桿動響應信號傳遞能力進行驗證。分別在陶瓷桿頂部與底部安裝加速度傳感器后對結構進行掃頻，掃頻范圍覆蓋被測結構前2 階模態頻率（1～30 Hz），測得加速度響應信號如圖15 所示。由掃頻試驗結果可知，二者信號相位完全一致，僅信號幅值在部分頻段有細微差別，說明陶瓷桿的引入不會為試驗系統在關注頻帶內引入新模態，且其能夠較為準確傳遞結構響應信號，因此陶瓷桿能夠在地面熱顫振模擬試驗中被用于傳遞結構響應信號。

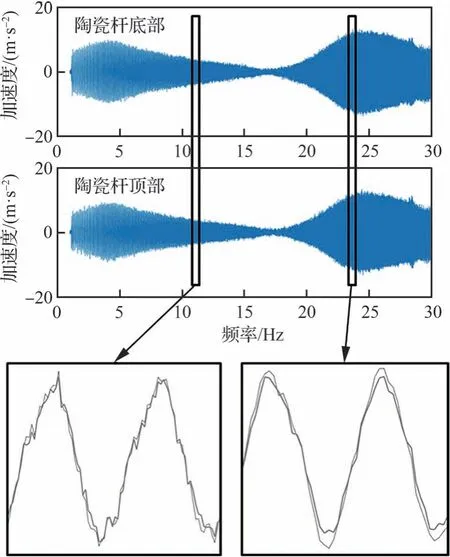
圖15 掃頻響應信號對比Fig.15 Comparison of swept-frequency response signal

4.3 激勵力加載控制

在地面顫振模擬試驗中，激振器之間會通過被測結構相互影響，為了降低這種耦合效應導致的激勵力加載偏差，本研究采用H∞魯棒控制算法針對多激振器加載系統設計控制器［15］。

首先建立被控對象的狀態空間模型。建模以掃頻試驗數據為基礎，采用子空間辨識法進行，即首先構建輸入輸出信號的Hankel 矩陣，再將該矩陣斜投影并奇異值分解獲得系統的可觀測矩陣及卡爾曼狀態序列，最后通過最小二乘法等算法即可獲得系統狀態空間矩陣。

為了簡化控制器設計工作，將混合靈敏度設計方法引入標準H∞控制問題如圖16 所示，在確定3 個加權矩陣W1，W2與W3后，即可通過Riccati方程或線性矩陣不等式（LMI）完成控制器求解。

圖16 混合靈敏度標準H∞控制問題Fig.16 Mixed sensitivity standard H∞ control problem

5 試驗測試與結果分析

將氣動熱環境模擬系統與地面顫振試驗系統集成開展試驗，其中采用激光位移傳感器測量節點位移信號并微分獲得速度信號，采用加速度傳感器測量節點加速度信號，非定常氣動力計算及魯棒控制算法由N（INational Instruments）半實物仿真系統實現。圖17為熱顫振地面模擬試驗現場。

圖17 熱顫振地面模擬試驗現場Fig.17 Thermal flutter ground simulation test site

試驗初始空速設置為2 800 m/s，在試驗開始約5 s 時開啟顫振臨界速度跟蹤系統，試驗所得結構監測點響應與顫振臨界速度曲線如圖18所示。

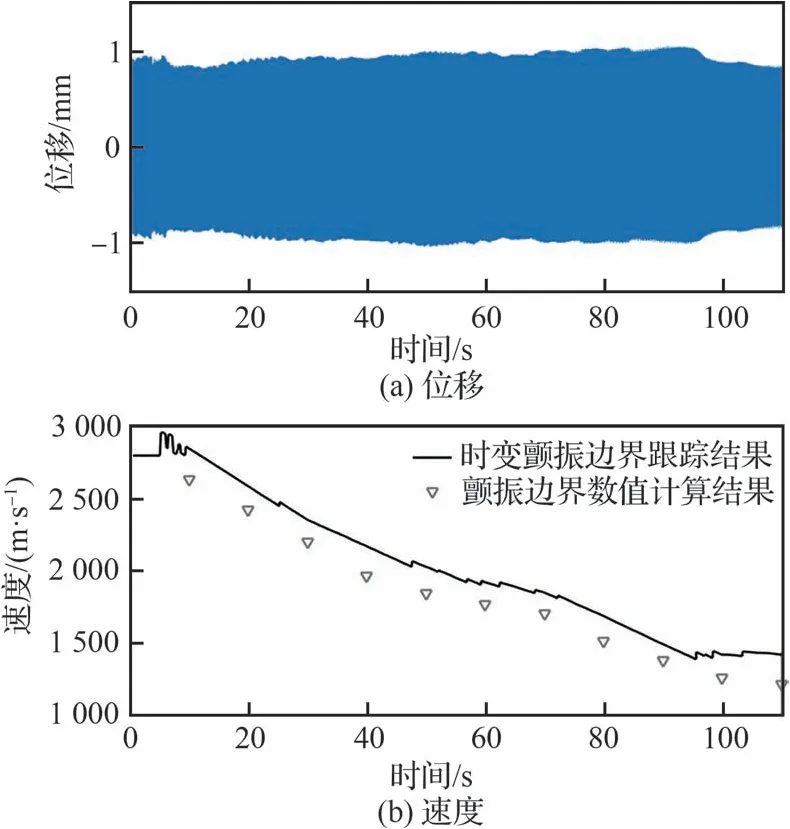
圖18 熱顫振地面模擬試驗結果Fig.18 Thermal flutter ground simulation test result

由圖18 可以看出，結構響應幅值整體變化不大，近似于等幅振動，且速度曲線時變趨勢與圖9所示本試驗系統的仿真結果基本一致，說明顫振臨界速度跟蹤模塊在試驗系統中運行正常。值得注意的是，由3.3 節可知該速度跟蹤模塊是根據已有的結構響應信號變化趨勢判斷試驗速度修正量，其修正過程具有一定滯后性，因此圖18中結構響應并非理想情況下的等幅振蕩，而是在10～90 s 間的緩慢發散以及90～110 s 間的緩慢收斂。參考此類地面顫振模擬試驗中結構響應收斂或顫振發散的時間尺度［16］，這種極其緩慢的結構響應變化說明試驗速度與結構實際顫振臨界速度非常接近，并不影響顫振臨界速度跟蹤模塊輸出結果的可信度。

選取工況點所處時間點的速度跟蹤數據（即10 的整數倍處時間節點）并與對應工況點的數值計算結果（圖中三角形標記點）作對比，如表2所示。

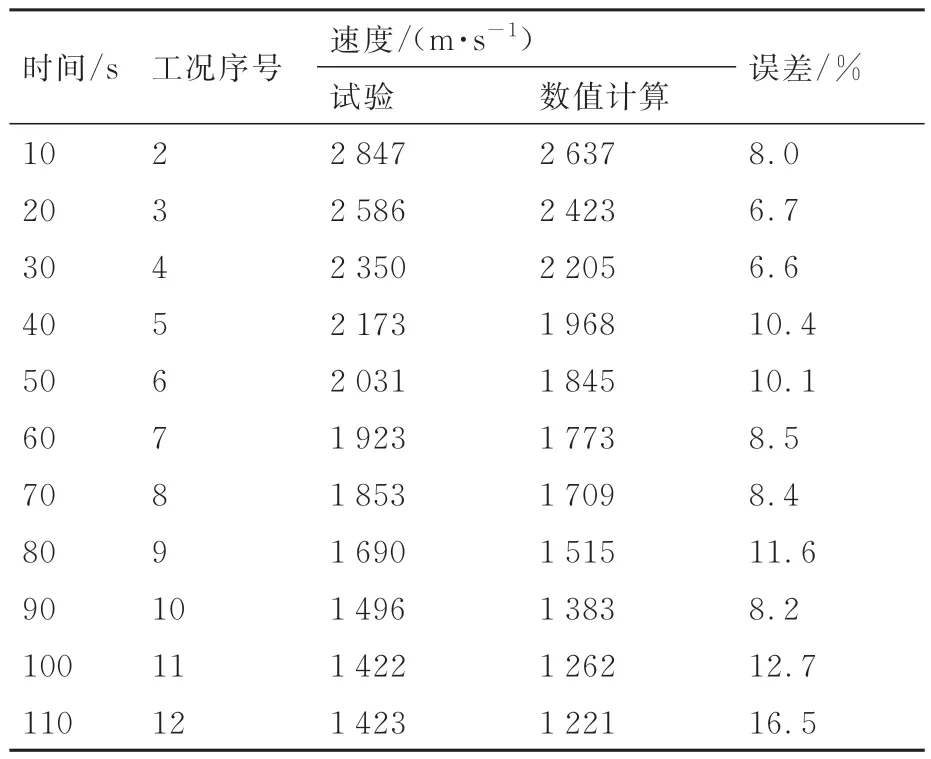
表2 試驗結果及誤差Table 2 Test results and errors

由表2 可知，試驗所得顫振臨界速度整體大于數值計算結果，由于顫振數值計算中未考慮結構阻尼，試驗結果整體偏大是合理的，但是由于二者間誤差處于較高水平，為進一步優化地面熱顫振模擬試驗技術，提升試驗精度，對可能導致較大誤差的原因分析如下：

1） 本次試驗仍然沿用了目前在地面顫振模擬試驗中普遍采用的魯棒控制器作為激勵力控制方法。對于熱顫振系統而言，隨著溫度升高結構動力學特性會發生顯著改變，顫振頻率顯著降低，在應對此類動力學系統時魯棒控制器存在2 個缺陷：一是魯棒控制器求解采用的單一狀態結構辨識模型難以反映系統在整個時變歷程中的動力學特性；二是魯棒控制器存在控制頻帶較窄的固有缺陷，因此當結構顫振頻率改變至控制器控制頻帶之外時，力加載精度會顯著下降，在試驗進程后期（100～110 s）由于系統顫振頻率已經偏離控制器設計頻帶，由表2 可以看出，此時試驗誤差顯著增大。綜上所述，魯棒控制器的固有缺陷使其并不能完全滿足熱顫振地面模擬試驗中的力控制要求，從而導致了較大的試驗誤差，因此針對熱顫振地面模擬試驗的氣動力精準加載技術還值得進一步研究。

2） 考慮到石英燈加熱系統的加載偏差，實際試驗中結構的溫度場與數值計算采用的并不完全一致，雖然由熱模態試驗可知該溫度場模擬偏差在誤差允許范圍內，但仍會對最終試驗結果造成一定影響；此外，由于熱試驗系統與地面顫振試驗系統相互獨立，試驗過程中需要人工操作實現2 套系統的并行，其運行的時間差會導致數值計算與實際試驗的溫度場不一致。對于熱顫振系統而言，其顫振臨界速度對溫度場變化是較為敏感的，因此溫度場與氣動力模型的匹配誤差也會為試驗最終結果引入一定誤差。

6 結 論

1） 氣動熱效應會使結構的顫振邊界發生顯著改變，因此研究高超聲速飛行器在不同航跡下的熱顫振邊界對于保證其可靠性具有重大意義。

2） 本文提出的針對時變溫度場中結構的非定常氣動力模型重構方法及時變顫振邊界控制跟蹤方法在試驗中應用效果良好，有效彌補了當前技術手段無法考慮氣動參數時變特性的缺陷，拓展了地面顫振模擬試驗的適用范圍。

3） 試驗采用的石英燈輻射加熱系統能夠較好的模擬結構承受的氣動熱效應，且氧化鋁陶瓷桿能夠較為準確地傳遞結構振動響應信號，克服高溫環境為振動信號獲取帶來的障礙，滿足熱顫振地面模擬試驗需求。

4） 研究結果表明，熱顫振地面模擬試驗是一種可行的熱顫振試驗驗證手段，在控制器有效控制頻帶內，測試結果精度滿足工程要求，但是對于頻率變化劇烈的情況，仍需開展進一步研究以拓寬控制器的工作頻帶，擴展技術的適用范圍。