基于組合預(yù)測(cè)的蘇州市物流需求預(yù)測(cè)分析
呂婉琪,陸芬

摘? 要:隨著科技與國(guó)民經(jīng)濟(jì)的發(fā)展,物流早已作為人類生活的必需品貫穿于日常的各個(gè)層面。發(fā)展壯大物流業(yè)有利于提升國(guó)家經(jīng)濟(jì)運(yùn)行效率,完善資源分配,推進(jìn)企業(yè)的融資以及促進(jìn)整個(gè)社會(huì)經(jīng)濟(jì)運(yùn)行結(jié)構(gòu)的調(diào)整。中國(guó)物流業(yè)發(fā)展迅速的背后是經(jīng)濟(jì)的支持,而產(chǎn)業(yè)結(jié)構(gòu)的升級(jí)和經(jīng)濟(jì)的提質(zhì)增效也離不開(kāi)物流業(yè)的成長(zhǎng),經(jīng)濟(jì)發(fā)展與物流發(fā)展相輔相成。因此,為了更好地制定物流計(jì)劃并推動(dòng)經(jīng)濟(jì)發(fā)展,物流需求預(yù)測(cè)就顯得十分重要。文章選取蘇州市作為研究對(duì)象,通過(guò)運(yùn)用蘇州市的綜合貨運(yùn)量與GDP等重要經(jīng)濟(jì)指標(biāo),分別在二次指數(shù)平滑法和回歸分析預(yù)測(cè)法下進(jìn)行綜合貨運(yùn)量的預(yù)測(cè),對(duì)比兩種方法的相對(duì)誤差,確定未來(lái)三年蘇州市綜合貨運(yùn)量的預(yù)測(cè)值,并對(duì)蘇州市物流提出管理建議,以期為蘇州市的經(jīng)濟(jì)發(fā)展提供借鑒。
關(guān)鍵詞:物流需求預(yù)測(cè);二次指數(shù)平滑法;回歸分析預(yù)測(cè)法
中圖分類號(hào):F259.27? ? 文獻(xiàn)標(biāo)志碼:A
DOI:10.13714/j.cnki.1002-3100.2023.11.009
Abstract: With the development of science and technology and national economy, logistics has long been a necessity of human life throughout every level of daily life. The development and expansion of the logistics industry is conducive to enhancing the efficiency of national economic operation, improving resource allocation, promoting enterprise financing, and advancing the adjustment of the entire socio-economic operation structure. The rapid development of China logistics industry is supported by the economic, and the upgrading of industrial structure and the improvement of economic quality and efficiency can not be separated from the growth of the logistics industry. The development of economic and logistics complement each other. Therefore, in order to better formulate logistics plans and promote economic development, logistics demand forecasting is very important. Suzhou City is selected as the research object. By using the comprehensive freight volume, GDP and other important economic data of Suzhou, the comprehensive freight volume is predicted under the second exponential smoothing method and regression analysis prediction method. The relative errors of the two methods are compared to determine the predictive value of the comprehensive freight volume of Suzhou in the next three years, and the management suggestions for Suzhou logistics are put forward to provide reference for the economic development of Suzhou.
Key words: logistics demand forecast; second exponential smoothing method; regression analysis prediction method
0? 引? 言
隨著科技的進(jìn)步和時(shí)代的更迭,物流業(yè)發(fā)展迅速。古有驛站傳信,今有高科技自動(dòng)機(jī)器人智能分揀快遞,物流的技術(shù)可謂是日新月異。如今,為了促進(jìn)銷售、帶動(dòng)消費(fèi)者的內(nèi)需,商家經(jīng)常舉辦促銷活動(dòng)。電商平臺(tái)和快遞行業(yè)的興起,更是促進(jìn)了消費(fèi)者購(gòu)買商品的熱情。根據(jù)國(guó)家郵政局統(tǒng)計(jì),2021年“雙11”期間(11月1日至16日),郵政、中通等快遞企業(yè)共攬收快遞包裹68億件,同比增長(zhǎng)18.2%。“雙11”當(dāng)天,天貓總交易額為5 403億元。由此可見(jiàn),快遞給人們生活帶來(lái)的便利促進(jìn)了物流行業(yè)的迅速發(fā)展,同時(shí)物流業(yè)的發(fā)展折射出了中國(guó)經(jīng)濟(jì)旺盛的內(nèi)需、加速轉(zhuǎn)型的步伐與廣闊的發(fā)展?jié)摿Α?/p>
物流需求預(yù)測(cè)主要是為了引導(dǎo)和協(xié)調(diào)人們的物流管理活動(dòng),從而幫助人們采取適當(dāng)?shù)牟呗院褪侄蝸?lái)謀求最大的利益[1]。這意味著,精確的需求預(yù)測(cè)不僅可以促進(jìn)物流信息系統(tǒng)和生產(chǎn)設(shè)施能力的計(jì)劃和協(xié)調(diào),還可以確定產(chǎn)品向配送中心、倉(cāng)庫(kù)或零售商進(jìn)行分配的原則[2]。由于物流產(chǎn)業(yè)與經(jīng)濟(jì)不可分割的關(guān)系,因此對(duì)一個(gè)地區(qū)的物流需求進(jìn)行分析與預(yù)測(cè)可以直觀地看出該地區(qū)的經(jīng)濟(jì)發(fā)展情況:隨著區(qū)域經(jīng)濟(jì)結(jié)構(gòu)、資源配置、市場(chǎng)等多種經(jīng)濟(jì)因素的變化,區(qū)域的物流需求量、物流需求結(jié)構(gòu)和物流需求層次也會(huì)發(fā)生相應(yīng)的變化[3]。鑒于此,研究物流需求預(yù)測(cè)對(duì)于了解經(jīng)濟(jì)發(fā)展情況十分重要。
關(guān)于物流預(yù)測(cè)的研究中,牛娜通過(guò)分析區(qū)域物流發(fā)展與地方農(nóng)業(yè)經(jīng)濟(jì)發(fā)展之間的關(guān)系,研究了區(qū)域物流合理化預(yù)測(cè)對(duì)地方農(nóng)業(yè)經(jīng)濟(jì)發(fā)展的影響[3]。陳長(zhǎng)英將傳統(tǒng)的灰色預(yù)測(cè)模型和馬爾可夫鏈相結(jié)合,通過(guò)建立改進(jìn)的預(yù)測(cè)模型對(duì)廣西物流需求進(jìn)行了預(yù)測(cè)[4]。梁永年等通過(guò)相關(guān)系數(shù)發(fā)現(xiàn)惠州市GDP與綜合貨運(yùn)量之間密切相關(guān),分別運(yùn)用線性回歸法和彈性系數(shù)法對(duì)惠州市物流需求量進(jìn)行預(yù)測(cè)[5]。黃凱和王健圍繞生鮮農(nóng)產(chǎn)品冷鏈物流需求分別采用GM1,1、BP神經(jīng)網(wǎng)絡(luò)和RBF神經(jīng)網(wǎng)絡(luò)方法來(lái)進(jìn)行預(yù)測(cè)[6]。王佳穎等發(fā)現(xiàn)BP神經(jīng)網(wǎng)絡(luò)模型較強(qiáng)的泛化能力,在預(yù)測(cè)青島港口物流需求時(shí)有良好的表現(xiàn)[7]。樊東方等為了應(yīng)對(duì)現(xiàn)有中長(zhǎng)期宏觀物流量預(yù)測(cè)模型的局限性和對(duì)我國(guó)宏觀物流量進(jìn)行預(yù)測(cè)分析,提出基于pccsAMOPSO算法的多目標(biāo)變權(quán)組合預(yù)測(cè)模型[8]。雷蕾等運(yùn)用貴州省貨運(yùn)周轉(zhuǎn)量數(shù)據(jù)在灰色GM1,1模型下進(jìn)行了物流需求量預(yù)測(cè)[9]。冉茂亮等將集成經(jīng)驗(yàn)?zāi)B(tài)分解(EEMD)、局部均值分解(LMD)、長(zhǎng)短期記憶網(wǎng)絡(luò)(LSTM)和局部誤差校正(LEC)代入模型,在EEMD-LMD-LSTM-LEC模型下進(jìn)行了物流預(yù)測(cè)[10]。
本文選取蘇州市作為研究對(duì)象,基于GDP等重要經(jīng)濟(jì)指標(biāo),采用二次指數(shù)平滑法和回歸分析預(yù)測(cè)法對(duì)蘇州市綜合貨運(yùn)量進(jìn)行分析,將綜合貨運(yùn)量的實(shí)際值和兩種方法得到的預(yù)測(cè)值進(jìn)行比較。通過(guò)對(duì)比兩種方法的相對(duì)誤差,選擇相對(duì)誤差較小的方法對(duì)未來(lái)三年蘇州市綜合貨運(yùn)量進(jìn)行預(yù)測(cè),以期為蘇州市物流發(fā)展提供數(shù)據(jù)借鑒。
1? 蘇州市物流現(xiàn)狀
蘇州地處中國(guó)華東地區(qū)、江蘇東南部、長(zhǎng)三角中部,是揚(yáng)子江城市群重要組成部分,東臨上海、南接嘉興、西抱太湖、北依長(zhǎng)江。鑒于其優(yōu)越的地理位置,蘇州市一直是我國(guó)重要的物流轉(zhuǎn)運(yùn)中心城市之一。蘇州是Adidas、黛珂、無(wú)印良品等大型企業(yè)倉(cāng)儲(chǔ)和快遞轉(zhuǎn)運(yùn)的中心。雙十一等大促期間蘇州倉(cāng)儲(chǔ)經(jīng)常出現(xiàn)的爆倉(cāng)情況給許多快遞企業(yè)、商家和消費(fèi)者帶來(lái)了困擾。因此,對(duì)蘇州市物流貨運(yùn)量進(jìn)行預(yù)測(cè),可以幫助蘇州市更好地制定相應(yīng)的物流管理計(jì)劃,更快速地應(yīng)對(duì)突發(fā)的情況。
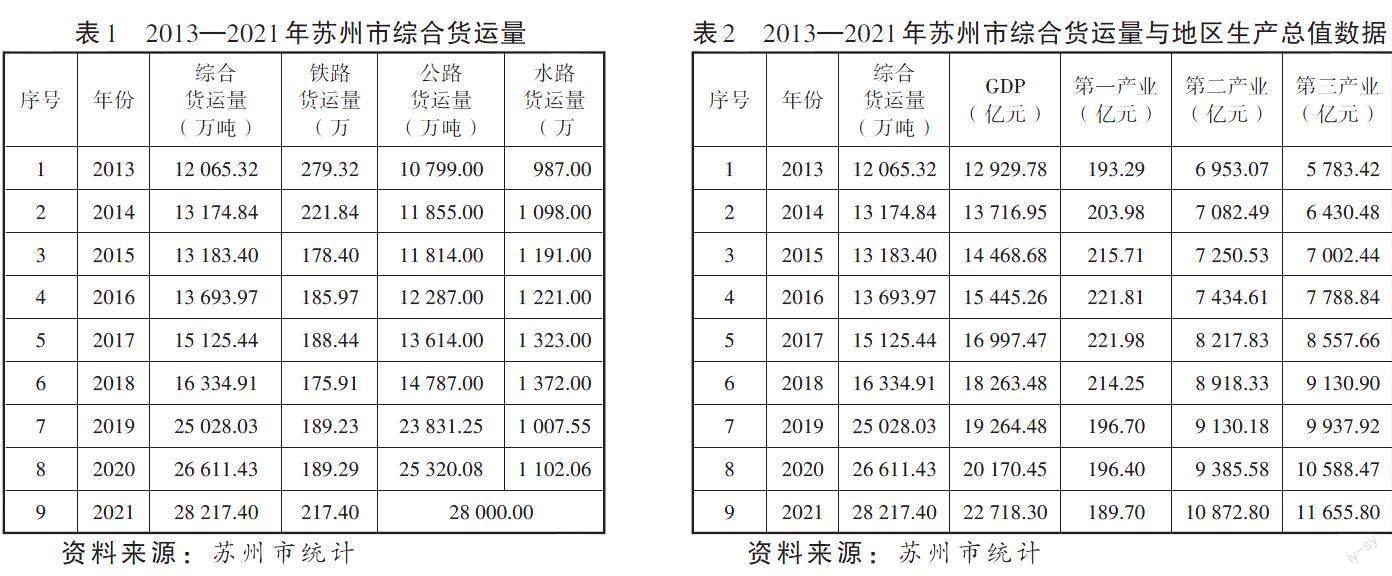
根據(jù)蘇州市統(tǒng)計(jì)局2013年至2020年的統(tǒng)計(jì)年鑒和2021年蘇州市統(tǒng)計(jì)公報(bào),蘇州市綜合貨運(yùn)量的具體數(shù)據(jù)如表1所示,其中綜合貨運(yùn)量由鐵路貨運(yùn)量、公路貨運(yùn)量和水路貨運(yùn)量三部分組成。
由于物流需求量通常用綜合貨運(yùn)量進(jìn)行衡量,且經(jīng)濟(jì)發(fā)展與物流發(fā)展之間存在著一定關(guān)系,因此表2收集整理了綜合貨運(yùn)量、GDP、第一產(chǎn)業(yè)、第二產(chǎn)業(yè)和第三產(chǎn)業(yè)的數(shù)據(jù)作為預(yù)測(cè)所需的基礎(chǔ)數(shù)據(jù)。
為更加直觀地了解蘇州市經(jīng)濟(jì)運(yùn)行情況與綜合貨運(yùn)量的關(guān)系,通過(guò)Excel表格軟件的數(shù)據(jù)分析得到蘇州市綜合貨運(yùn)量與經(jīng)濟(jì)指標(biāo)之間的關(guān)系[5],如表3所示。
根據(jù)表3,與蘇州市綜合貨運(yùn)量密切相關(guān)的經(jīng)濟(jì)指標(biāo)為GDP(0.929 5)、第二產(chǎn)業(yè)(0.918 3)和第三產(chǎn)業(yè)(0.928 3)。這說(shuō)明GDP、第二產(chǎn)業(yè)和第三產(chǎn)業(yè)與綜合貨運(yùn)量之間存在比較強(qiáng)的正相關(guān)關(guān)系,這些指標(biāo)均可用于蘇州市綜合貨運(yùn)量的預(yù)測(cè)。由于GDP與綜合貨運(yùn)量的相關(guān)性最強(qiáng),因此采用GDP來(lái)預(yù)測(cè)蘇州市的綜合貨運(yùn)量。
2? 蘇州市物流需求預(yù)測(cè)建模
2.1? 二次指數(shù)平滑法
指數(shù)平滑法是依托于移動(dòng)平均法發(fā)展起來(lái)的,其實(shí)質(zhì)上是一種特殊的加權(quán)移動(dòng)平均法[11]。指數(shù)平滑法包括一次指數(shù)平滑法和二次指數(shù)平滑法等。由于一次指數(shù)平滑法不能進(jìn)行有明顯趨勢(shì)波動(dòng)的數(shù)據(jù)預(yù)測(cè),且一次指數(shù)平滑法存在只能預(yù)測(cè)未來(lái)一期數(shù)據(jù)的缺陷,因此本文選擇二次指數(shù)平滑法進(jìn)行預(yù)測(cè)。
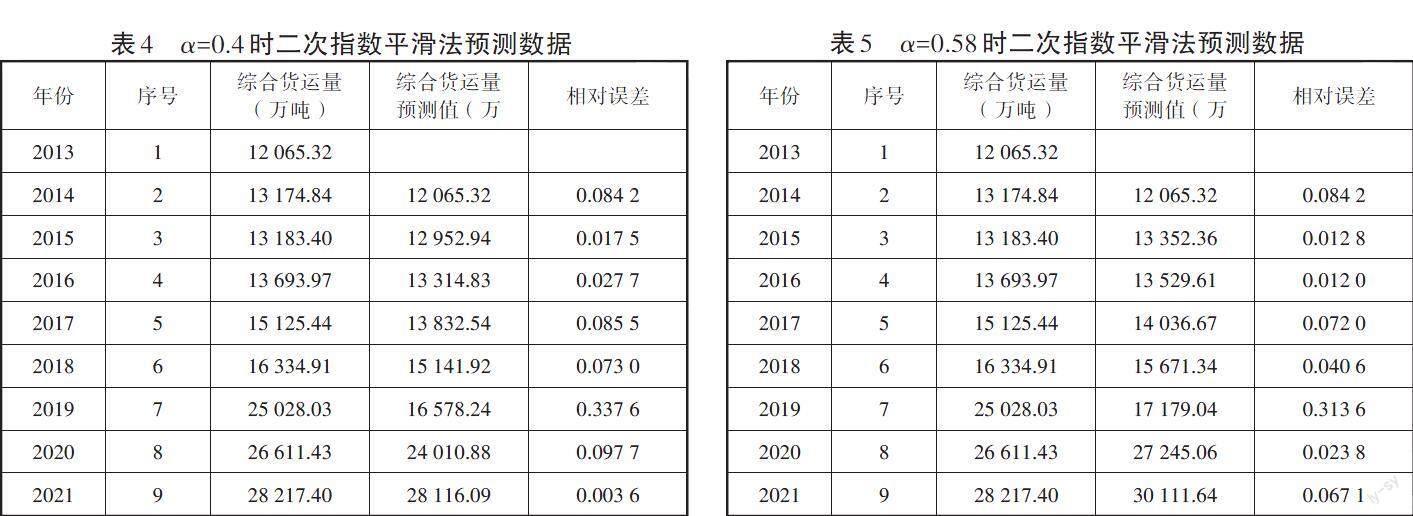
根據(jù)指數(shù)平滑系數(shù)α的選取原則,本文選取0.4作為α的值,將第一期的實(shí)際值(即2013年的綜合貨運(yùn)量)作為第一次預(yù)測(cè)的初始值,根據(jù)二次指數(shù)平滑法的公式與計(jì)算步驟,將綜合貨運(yùn)量的實(shí)際值、預(yù)測(cè)值和相對(duì)誤差分別列于表4。
當(dāng)α=0.4時(shí),MSE(均方誤差)為10 336 868.995。雖然表4中的相對(duì)誤差較小,但本文在選取指數(shù)平滑系數(shù)α?xí)r具有一定的主觀性。因此,為保證預(yù)測(cè)值的最優(yōu)性,通過(guò)運(yùn)用Excel表格軟件中的模擬運(yùn)算表,將0.01至0.99(α的精確度為小數(shù)點(diǎn)后兩位)之間的所有數(shù)值分別作為指數(shù)平滑系數(shù)α進(jìn)行模擬運(yùn)算[12],找到最優(yōu)α值。通過(guò)計(jì)算發(fā)現(xiàn)當(dāng)α=0.58時(shí),其MSE最小,此時(shí)MSE*=8 563 586.2。鑒于此,運(yùn)用最優(yōu)指數(shù)平滑系數(shù)α=0.58再次進(jìn)行預(yù)測(cè),得到表5的數(shù)據(jù)。
將表4與表5中的相對(duì)誤差進(jìn)行對(duì)比,繪制圖像如圖1所示。觀察該圖可以發(fā)現(xiàn),α=0.58時(shí)的相對(duì)誤差大體上離軸更近,進(jìn)一步驗(yàn)證了上文的結(jié)論(α=0.58是最優(yōu)指數(shù)平滑系數(shù))。
2.2? 回歸分析預(yù)測(cè)法
回歸分析預(yù)測(cè)法依托于自變量與因變量之間的關(guān)系,是通過(guò)建立變量之間的回歸方程進(jìn)行預(yù)測(cè)的。根據(jù)自變量與因變量的相關(guān)關(guān)系不同,回歸分析預(yù)測(cè)法可分為線性回歸預(yù)測(cè)和非線性回歸預(yù)測(cè)[2]。回歸分析預(yù)測(cè)法也是預(yù)測(cè)的一種重要方法,常常用于中短期數(shù)據(jù)的預(yù)測(cè)。具體步驟為:首先,根據(jù)預(yù)測(cè)目標(biāo),確定自變量與因變量;其次,建立回歸預(yù)測(cè)模型,進(jìn)行相關(guān)分析;再次,檢驗(yàn)回歸預(yù)測(cè)模型,計(jì)算出相對(duì)預(yù)測(cè)誤差;最后,確定預(yù)測(cè)值[13]。
觀察表2和表3,可以看出GDP與年份、綜合貨運(yùn)量與GDP之間均存在正相關(guān)關(guān)系,因此本文將分別采取線性回歸預(yù)測(cè)進(jìn)行分析。
首先,通過(guò)建立GDP與年份關(guān)系的回歸方程預(yù)測(cè)GDP的數(shù)值。將年份作為自變量x,GDP作為因變量y,通過(guò)SPSS進(jìn)行線性回歸分析,得到如圖2所示的系數(shù)表格。根據(jù)圖2可以看出,GDP與年份的回歸方程為y=1 182.08x-2 367 155.08。
同時(shí),繪制GDP與年份的散點(diǎn)圖及回歸方程,如圖3所示。
與上文相同,再將GDP作為自變量y,綜合貨運(yùn)量作為因變量z,進(jìn)行線性回歸分析,得到圖4所示的系數(shù)表格。根據(jù)圖4可以看出,綜合貨運(yùn)量與GDP之間的回歸方程為z=1.85y-13 496.43。
同理,根據(jù)綜合貨運(yùn)量與GDP的關(guān)系繪制散點(diǎn)圖和回歸方程,如圖5所示。
最后,在已知GDP與年份、綜合貨運(yùn)量與GDP關(guān)系的回歸方程之后,首先通過(guò)GDP與年份的回歸方程y=1 182.08x-2 367 155.08計(jì)算GDP的預(yù)測(cè)值;再基于綜合貨運(yùn)量與GDP之間的回歸方程z=1.85y-13 496.43,將預(yù)測(cè)的GDP數(shù)據(jù)代入自變量中,計(jì)算出綜合貨運(yùn)量的預(yù)測(cè)值,進(jìn)一步得到綜合貨運(yùn)量實(shí)際值與預(yù)測(cè)值之間的相對(duì)誤差,如表6所示。
2.3? 對(duì)比與預(yù)測(cè)分析
為找出二次指數(shù)平滑法和回歸分析預(yù)測(cè)法二者中更優(yōu)的預(yù)測(cè)方法,將表5與表6中的相對(duì)誤差進(jìn)行比較,通過(guò)運(yùn)用相對(duì)誤差較小的預(yù)測(cè)方法,確定2022年、2023年和2024年蘇州市綜合貨運(yùn)量的預(yù)測(cè)值。兩種方法相對(duì)誤差的比較如圖6所示。
根據(jù)圖6可以看出:
(1)二次指數(shù)平滑法的相對(duì)誤差總體上比回歸分析預(yù)測(cè)法的相對(duì)誤差小。
(2)二次指數(shù)平滑法下預(yù)測(cè)值更接近于實(shí)際值。
因此,根據(jù)二次指數(shù)平滑法的公式Y(jié)■=a■+b■T進(jìn)行2022年、2023年和2024年綜合貨運(yùn)量預(yù)測(cè),其中a■和b■為2021年預(yù)測(cè)過(guò)程中的計(jì)算結(jié)果,且a■=28 551.54,b■=2 751.21。具體預(yù)測(cè)值如表7所示。
3? 蘇州市物流業(yè)發(fā)展建議
雖然蘇州市物流管理已經(jīng)有一套相對(duì)完備的系統(tǒng),但其仍可以從以下兩個(gè)方面進(jìn)行改進(jìn):
(1)完善物流運(yùn)輸流程。由于大部分物流運(yùn)輸業(yè)務(wù)均通過(guò)公路運(yùn)輸完成,因此蘇州市可以在大促期間簡(jiǎn)化物流運(yùn)輸流程,開(kāi)設(shè)快遞專用高速通道。這種舉措不僅可以提高快遞運(yùn)輸效率,還可以在一定程度上增加單位貨運(yùn)量,吸引更多的電商在此建立倉(cāng)庫(kù),從而加快蘇州市經(jīng)濟(jì)發(fā)展的步伐。
(2)合理規(guī)劃物流路線,建立物流園區(qū)。根據(jù)預(yù)測(cè),蘇州市未來(lái)三年的綜合貨運(yùn)量呈逐年遞增的趨勢(shì)。通過(guò)對(duì)物流路徑的優(yōu)化既可以節(jié)省運(yùn)輸時(shí)間,又可以緩解城市交通擁擠的問(wèn)題。對(duì)物流運(yùn)輸車輛的時(shí)間限制也可以起到相同的作用。同時(shí),蘇州市還可以將較小的臨近物流園區(qū)重新規(guī)劃,組建成一個(gè)較大的綜合物流園。這樣做既推動(dòng)了城市的進(jìn)一步規(guī)劃,又在一定程度上滿足了物流企業(yè)周轉(zhuǎn)的需求。
4? 結(jié)? 論
物流與經(jīng)濟(jì)之間不可分割的關(guān)系表明物流發(fā)展可以帶動(dòng)經(jīng)濟(jì)發(fā)展。物流需求作為衡量物流發(fā)展水平的主要指標(biāo),對(duì)了解經(jīng)濟(jì)發(fā)展情況也有重要的參考作用。物流需求的預(yù)測(cè)可以幫助企業(yè)和政府提前制定相應(yīng)的對(duì)策以應(yīng)對(duì)突發(fā)情況。本文考慮重要經(jīng)濟(jì)指標(biāo),通過(guò)運(yùn)用二次指數(shù)平滑法和回歸分析預(yù)測(cè)法對(duì)蘇州市的綜合貨運(yùn)量進(jìn)行分析,發(fā)現(xiàn)二次指數(shù)平滑法下的綜合貨運(yùn)量預(yù)測(cè)值更接近于真實(shí)值,在二次指數(shù)平滑法下通過(guò)預(yù)測(cè)發(fā)現(xiàn)2022年、2023年和2024年的綜合貨運(yùn)量預(yù)測(cè)值分別為31 302.76萬(wàn)噸、34 053.97萬(wàn)噸和36 805.18萬(wàn)噸。基于上述分析,蘇州市可以通過(guò)進(jìn)一步完善物流運(yùn)輸流程、優(yōu)化物流路徑和建立綜合物流園區(qū)的方法更好地發(fā)展蘇州市的物流業(yè)。
參考文獻(xiàn):
[1] 孫明貴. 物流管理學(xué)[M]. 北京:北京大學(xué)出版社,2002.
[2] 王長(zhǎng)瓊. 物流系統(tǒng)工程[M]. 北京:高等教育出版社,2007.
[3] 牛娜. 區(qū)域物流需求合理化預(yù)測(cè)與我國(guó)農(nóng)業(yè)經(jīng)濟(jì)發(fā)展格局關(guān)系研究[J]. 農(nóng)業(yè)經(jīng)濟(jì),2019(3):139-141.
[4] 陳長(zhǎng)英. 基于改進(jìn)的灰色-馬爾可夫鏈模型的廣西物流需求預(yù)測(cè)研究[J]. 西部交通科技,2019(10):152-155.
[5] 梁永年,姚鎮(zhèn)城,蔣文博,等. 惠州物流需求預(yù)測(cè)研究——兼論惠州市綜合運(yùn)輸體系建設(shè)[J]. 物流工程與管理,2020,42(7):36-39.
[6] 黃凱,王健. 我國(guó)生鮮農(nóng)產(chǎn)品冷鏈物流需求預(yù)測(cè)分析:基于最優(yōu)組合模型[J]. 武漢理工大學(xué)學(xué)報(bào)(信息與管理工程版),2020,42(6):524-529.
[7] 王佳穎,頊玉卿,李媛. 基于神經(jīng)網(wǎng)絡(luò)的青島港口物流需求量預(yù)測(cè)研究[J]. 青島職業(yè)技術(shù)學(xué)院學(xué)報(bào),2021,34(6):70-76.
[8] 樊東方,羅凱,靳志宏. 基于pccsAMOPSO的宏觀物流量多目標(biāo)變權(quán)組合預(yù)測(cè)模型[J]. 大連海事大學(xué)學(xué)報(bào),2021,47(4):19-29.
[9] 雷蕾,吳潔,陳嘉星. 基于灰色GM1,1的貴州物流需求“十四五”預(yù)測(cè)分析[J]. 棗莊學(xué)院學(xué)報(bào),2022,39(5):78-84.
[10] 冉茂亮,陳彥如,楊新彪. 基于EEMD-LMD-LSTM-LEC深度學(xué)習(xí)模型的短時(shí)物流需求預(yù)測(cè)[J]. 控制與決策,2022,37(10):2513-2523.
[11] 張雪琴. 關(guān)于“指數(shù)平滑法”的研究[J]. 內(nèi)蒙古農(nóng)業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版),2006,27(4):153-156.
[12] 蔣昌軍. Excel環(huán)境下指數(shù)平滑預(yù)測(cè)法最優(yōu)平滑系數(shù)的確定[J]. 中國(guó)管理信息化,2012,15(2):13-15.
[13] 方威,肖衡,任湘郴. 基于線性回歸模型的物流需求預(yù)測(cè)分析[J]. 生產(chǎn)力研究,2009(12):94-95,110.

