基于幾何設計法的航空發動機有限頻域穩態抗擾控制器設計

陳佳杰，王繼強，張海波，胡忠志，陳新民

1．南京航空航天大學 能源與動力學院，南京 210016

2．中國科學院 寧波材料技術與工程研究所 先進制造技術研究所，寧波 315201

3．清華大學 航空發動機研究院，北京 100084

巡航穩態工況一般為民航客機在整個飛行航線中時間最長的工況。飛機在保持長航時穩態工況的過程中，航空發動機會受到各種各樣的內部和外部干擾。外部環境干擾主要包括雨雪冰天氣干擾、大氣湍流干擾和電磁干擾等。這些環境干擾會對發動機進口氣流場造成影響，進而造成發動機內部部件性能參數不穩定；內部干擾主要包括傳感器、執行機構等部件造成，以及旋轉部件性能退化等。這些干擾對飛機保持巡航穩態的穩定性具有很大的隱患［1］。因此，穩態工況下的抗干擾問題一直是發動機控制的研究熱點。

對于航空發動機在巡航工況下可能遇到的各類外界干擾，其能量一般只集中分布在某一個或某些有限的頻率范圍內，如果在抗擾控制器設計時忽略干擾信號自身的有限頻域特性，設計的控制器往往具有較大的保守性。考慮到相同的干擾對發動機不同輸出性能量的影響也不盡相同，理想的發動機抗擾控制器設計方法應具備以下特征：① 可以在任何特定頻率或有限頻域內定量表征抗擾控制性能指標；② 可以在不增加反饋信號傳感器數目的情況下，對不同輸出性能量進行全局抗擾性能的定量優化；③ 可以直觀地在控制器設計階段基于理論進行面向全局抗擾性能的控制器設計。

現階段控制理論領域中，經典控制理論（PID、根軌跡法等）控制器設計方法核心是通過引入額外零極點來使閉環系統達到期望的頻率響應特性，整個設計過程面向的是全頻域，未能定義有限頻域指標，也無法滿足對不同輸出性能量進行全局抗擾性能的定量優化要求［2］。主動抗擾控制理論主要包括基于干擾觀測器的控制（DOBC）［3］和自抗擾控制（ADRC）［4-5］，雖然可以借助狀態觀測器估計干擾特性來在反饋回路中進行干擾補償，但同樣具有缺少控制器參數調節規范、無法直觀定義有限頻域內控制性能指標以及進行面向全局抗擾性能的控制器設計的不足之處。最優控制理論通常引入頻率加權函數來優化有限頻域性能，例如基于混合靈敏度的H∞控制方法［6-7］，但頻率加權函數的選擇大多數還是基于經驗，需要反復嘗試，而且基于頻率加權函數的研究方法屬于間接法，并不能提供被控對象在有限頻域性能的定量信息。有限頻Gramian 矩陣法［8］和廣義KYP 引理法［9-10］是直接基于有限頻域性能指標建立的控制理論，但同樣無法同時滿足這些特征，由于現有的有限頻Gramian 矩陣法定義的是系統的H2性能，對于特定頻率下的控制問題，有限頻Gramian 矩陣為0，無法計算系統的H2性能。廣義KYP 引理雖然可以在任何特定頻率或有限頻域內定量表征抗擾控制性能指標，但在設計控制器時由于需要額外引入權矩陣，導致了控制性能的保守性，并且對于不同的輸出性能量也無法根據需求進行全局抗擾性能的定量優化。

考慮到上述控制方法對于解決有限頻域抗擾問題的局限性，為了盡可能同時滿足理想抗擾控制器設計方法特征需求，本文提出一種能同時具備這些特征的控制器設計方法“幾何設計法”（Geometric Design Method，GDM）［11-12］。該方法目前已在振動控制以及能量收集領域取得了初步應用［13-14］，同時也為航空發動機穩態抗擾控制器的設計提供了一種新的思路方法和方向。對標理想發動機抗擾控制器設計方法的特征，幾何設計法控制理論的創新點可歸納為以下3 個方面：① 聚焦有限頻域內的抗擾性能進行控制器設計。幾何設計法提供了一種系統的靈敏度直觀整形方法，不引用依賴經驗法則設計的加權函數，直觀地建立了所設計的控制器與對應靈敏度函數頻率特性的定量關系，從而可以方便地聚焦在特定頻率或者有限頻域內進行抗擾控制器設計，忽略其他不重要頻域段的系統抗擾性能，大大降低了基于全頻段性能指標進行抗擾控制器設計的保守性。② 定量進行全局抗擾性能“折衷”。在頻域內尋求抗擾的“折衷”就是要求抗擾控制器在不同的頻率范圍內滿足不同的性能指標，這就意味著需要充分考慮并利用系統本身及干擾的頻率響應特性。幾何設計法將不同輸出量定義的性能指標通過坐標變換轉化為復平面上的若干個性能圓，因而可以在特定頻率或頻域下定量分析各個性能量之間的可折衷性，以及進行滿足需求的全局抗擾性能的“最優”“次優”控制器設計。③ 控制器設計過程的直觀性。幾何設計法最重要的創新點是在整個抗擾控制器設計過程中都能直觀地在復平面上表示出閉環系統各輸出量在特定頻率下的抗擾性能，以及控制量在受限情況下的系統抗擾性能極限，從而使用直觀的圖解法形式來解決有限頻域抗擾控制器的求取問題。

為了探究幾何設計法在航空發動機穩態抗擾領域的應用前景，本文根據幾何設計法控制理論，以某型先進齒輪傳動渦扇（Gear Turbofan，GTF）發動機模型為基礎，提出了基于幾何設計法的航空發動機穩態抗擾控制器設計技術路線，并在頻域和時域下分別研究了混合靈敏度H∞與GDM 控制器在巡航穩態工況馬赫數干擾作用下的抗擾效果，初步驗證了幾何設計法所具有的實現上述抗擾控制特征的優勢。

1 發動機建模及抗擾問題定義

本文所研究的發動機模型是一款30 000 磅（約合13.3×104N）推力級概念型GTF 發動機［15］，結構如圖 1 所示，相比傳統渦扇發動機，GTF 發動機的優勢如下：

1） 低壓軸和風扇軸通過齒輪箱連接，使得風扇可以在理想的低轉速下工作的同時可以保持低壓軸的高速旋轉，解決了風扇和低壓壓氣機不能同時在各自最佳轉速下工作的問題，提高了燃料效率并降低了燃氣輪機噪聲。

2） 引入了可變放氣活門（Variable Bleed Valve，VBV）來防止低壓壓氣機失速，以及風扇外涵可變面積尾噴口（Variable Area Fan Nozzle，VAFN）來保證風扇在各個工作點保持最佳效率，這2 個控制變量根據相應的調度計劃開環計算得到，不參與主回路控制。

GTF 發動機部件級模型基于NASA 開源的熱力學系統建模和分析工具箱［16］建立，除不包括起動模型外，適用于在全飛行包線進行仿真。模型中主燃油控制回路中的控制量為燃油流量，被控量為與推力線性相關度強的風扇折合轉速。

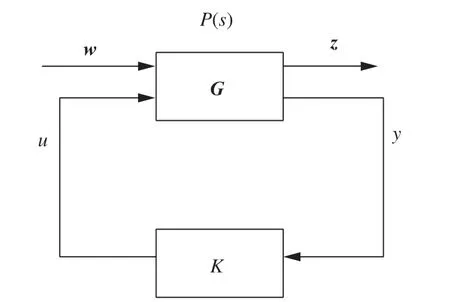
圖2 標準反饋控制結構Fig. 2 Standard feedback control structure diagram

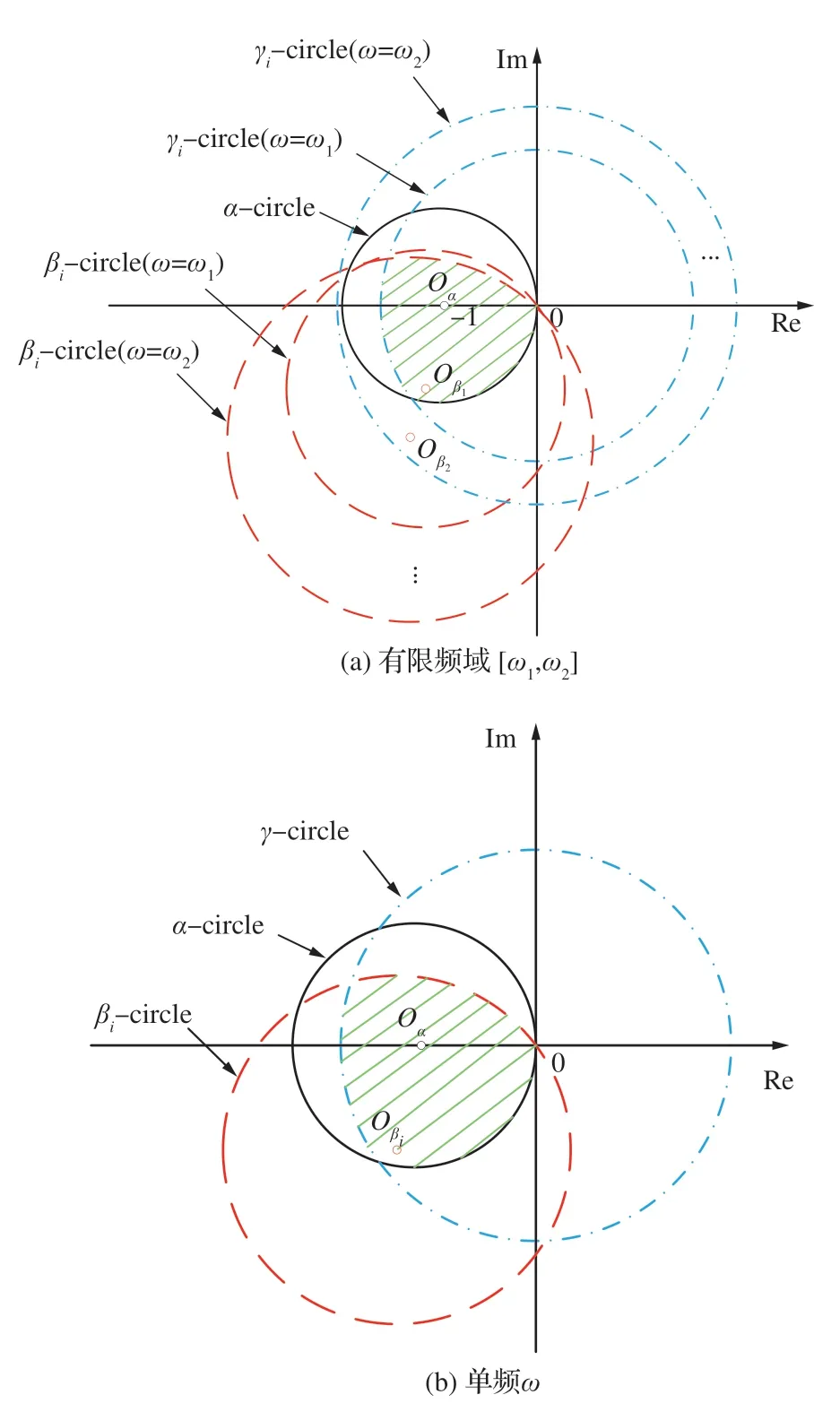
圖3 幾何設計法存在性問題在復平面上示意圖Fig. 3 Geometric design method schematic diagram in complex plane

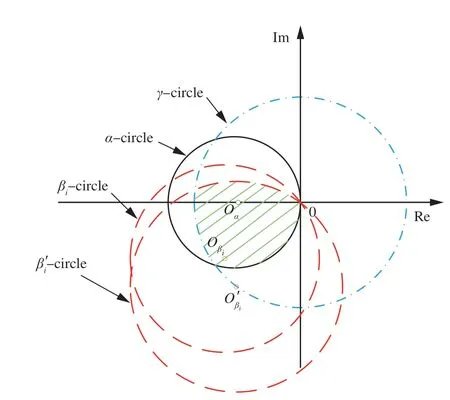
圖5 復平面上對應的魯棒控制器設計區域Fig. 5 Robust controller design scope in complex plane

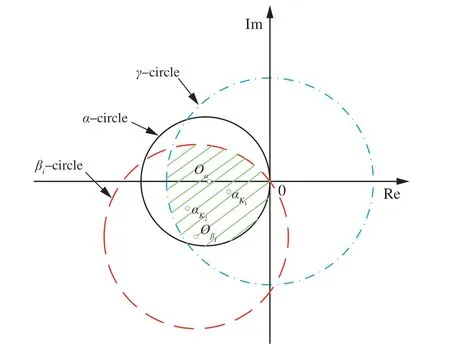
圖6 復平面上不同控制器性能比較Fig. 6 Different controller performances described in complex plane

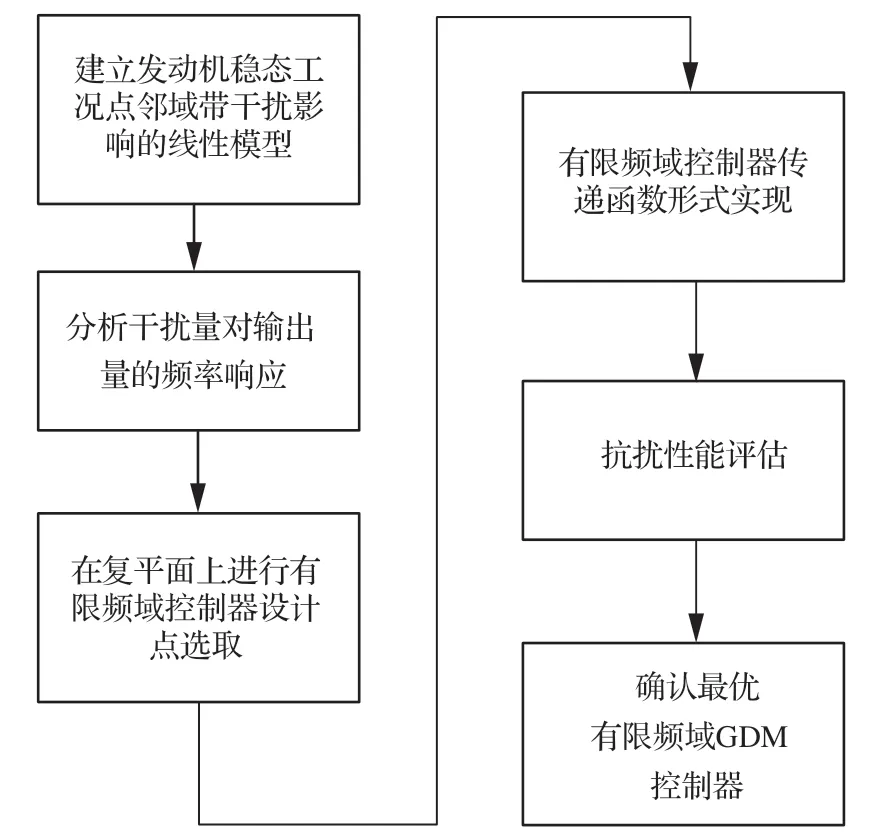
圖7 GDM 控制器設計流程Fig. 7 GDM controller design process

圖8 干擾對系統輸出的幅頻特性分析Fig. 8 Frequency domain analysis of transfer function from disturbance to outputs

本文研究的抗擾問題可以定義為，GTF 發動機在飛機巡航段長航時穩態飛行的情況下，會受到大氣湍流帶來的馬赫數干擾［17］，這會造成表征推力的風扇折合轉速的波動，然而實際發動機推力和風扇折合轉速的頻率特性并不相同，僅進行風扇折合轉速的抗擾控制器設計無法同時考慮到該控制器對推力的抗擾特性。因此，抗擾問題定義為設計一種主燃油控制回路的抗擾控制器，使得能在大氣干擾能量集中的有限頻域內，風扇折合轉速和推力均有較好的綜合抗擾性能，且盡可能地挖掘抗擾性能極限。

2 幾何設計理論介紹

幾何設計法的理論基于標準反饋控制結構，如圖 2 所示。

廣義被控對象P的傳遞函數矩陣可表示為

式中：

u表示控制量；w中變量表示外部輸入信號，包括各類干擾信號；y表示可用的反饋信號；z中變量是可控性能變量但不能用于反饋輸出。因此，設計目標是僅使用u=Ky反饋來控制整個結構系統，即達到對所有性能變量y和z的控制。雖然z不可用于反饋，但是可以假設在調試或建模階段可獲得傳遞函數矩陣G。

為了方便進行控制器設計，進一步假設輸入信號wi(jω)=Cid(jω)。其中，ω表示頻率；Ci是相對于單位輸入信號d(jω)的復數增益；i=1，2，…，n。由此式（1）可寫為

單位輸入信號d到輸出反饋信號y以及可控性能變量信號zi的傳遞函數為

單位輸入信號d到輸出反饋信號y以及可控性能變量信號zi的開環響應為

幾何設計法原理致力于在特定頻率點或有限頻域定義出性能極限的能力。對于特定頻率點ω或有限頻域[ω1，ω2]， 控制問題被重新定義為尋找控制器K，使得所有性能變量Tyd_c和(i=1，2，…，n) 在頻率ω處或有限頻域[ω1，ω2]上按相應抗擾性能需求衰減。這個問題包括存在性、最優性和控制綜合魯棒性3個子問題：

1） 存在性問題：僅使用u=Ky同時減少y(jω)和zi(jω)的可實現性。

2） 最優性問題：y(jω)和zi(jω)的最優性能。

3） 控制綜合魯棒性問題：針對給定全局抗擾性能指標，設計并實現強鎮定控制器K(s)，并且對于被控對象的內部不確定性，K(s)具有魯棒性。

為方便后續描述，定義靈敏度函數S、反饋靈敏度函數α及擾動靈敏度函數βi：

式中：

為表征控制器K作用后的抗擾性能，定義輸出量的性能指標η為輸出量閉環幅值和開環幅值之比，由式（3）～式（7）可得：

式中：δ1、δi為性能指標的需求，可根據實際抗擾需求進行更改。

控制器K的選取決定了反饋靈敏度函數α(jω)在復平面上的坐標，定義性能圓和控制量限制圓如下：

1） 性能圓（α、β圓）

由式（7）可得，滿足性能指標的α(jω)所在區域可以在復平面表示為以（-1，0）為圓心，δ1為半徑的圓，記作α圓，將δ1為1 的圓記作單位α圓。

2） 控制量限制圓（γ圓）

本文所研究的控制量燃油流量有很多限制，包括喘振、熄火邊界、渦輪前最大溫度、轉速、壓力等。巡航穩態工況下，定義控制量的范圍為

對于本文的控制問題，可轉化為

式中：us為穩態工況點對應的燃油流量。由u=Ky得

進而可得

限制圓體現在復平面上即為以（0，0）為圓心，半徑為rγ的圓區域內。

因此，特定頻率及有限頻域[ω1，ω2]內的受限抗擾控制問題的存在性和最優性問題便可通過圖形法來解決。針對引言給出的理想的抗擾控制器特征，分別提出命題如下。

命題1（存在性問題）當且僅當所有性能圓（α、β圓）和限制圓（γ圓）具有共同交點時，存在控制器u=Ky使得性能指標ηyd及同時減少。如圖 3 所示，圖 3（a）和圖 3（b）的陰影區域分別表示特定頻率及有限頻域[ω1，ω2]下使得性能指標ηyd及ηzid同時減少的控制器設計點α(jω)所在區域。

命題2（最優性問題）若存在一組δopt，δi_opt，使得性能圓（α、β圓）相切，且相切點位于限制圓（γ圓）內，則位于性能圓圓心連線所在直線上的相切點αopt所對應的控制器為該頻率下使得性能指標ηyd及能獲得最優全局抗擾性能的控制器，最優全局抗擾性能ηyd_opt及的分布滿足

式中：L代表兩點之間的距離。各抗擾性能指標（單位：dB）的幾何表達形式為

最優性/次優性問題的幾何設計圖如圖 4所示。

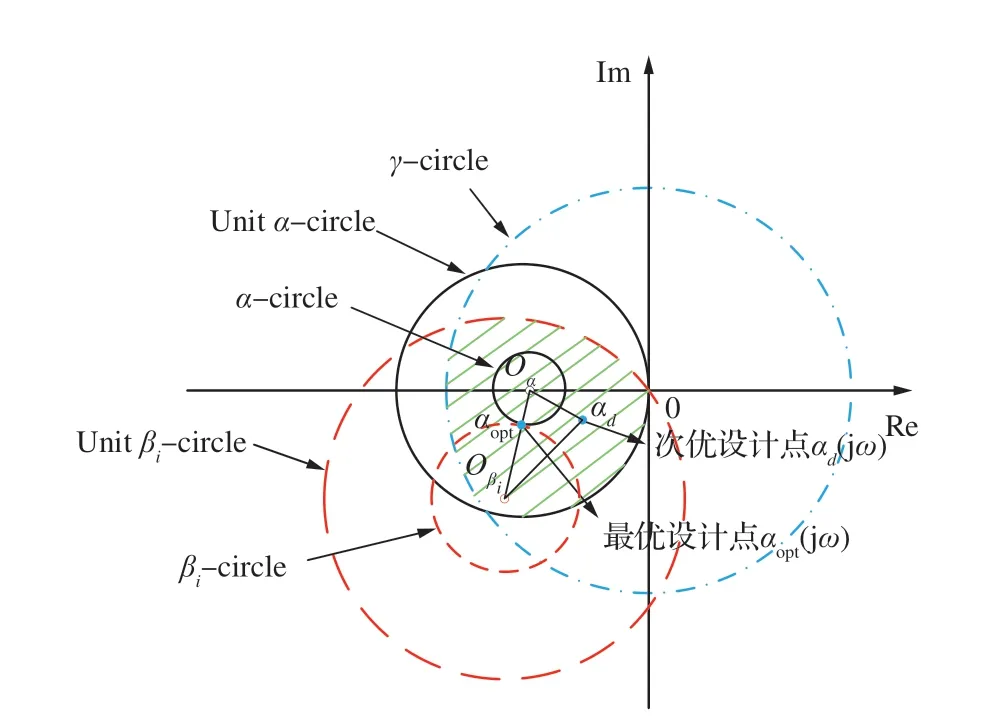
命題2 備注1δ1、δi決定了性能圓的半徑，式（15）直觀地構建了復平面上各輸出量的最優抗擾性能指標的幾何表達形式。根據性能圓圓心與控制器設計區域的位置關系，可分為如下4 種情況討論：

1）Oα和均位于控制器設計區域時，最優設計點αopt分別與Oα和重合時，則ηyd和分別具有極限抗擾性能。

2） 僅Oα位于控制器設計區域時，極限抗擾性能對應的最優設計點αopt位于與單位α圓的交點。

4）Oα和均不位于控制器設計區域時，極限抗擾性能對應的最優設計點αopt位于與單位α圓的交點；ηyd極限抗擾性能對應的最優設計點αopt位于與單位βi圓的交點。

命題2 備注2式（14）構建了復平面上各輸出量的最優抗擾性能指標的約束關系，用于直觀地描述系統所能達到的最優全局抗擾性能，由式（14）可知不同αopt坐標對應不同的最優全局抗擾性能，η越小代表抗擾性能越好。

命題2 備注3由于在實際工程中，最優全局抗擾性能可能存在無法實現的情況。可以根據實際控制需求合理調整全局抗擾性能指標，設計次優控制器。如圖 4 所示，根據三角形邊長幾何關系大小可得

次優全局抗擾性能ηyd及的分布滿足

各次優抗擾性能指標同樣滿足式（15）的幾何表達形式。

命題3（魯棒性問題）對于被控對象內部的不確定性對抗擾控制性能的影響，可轉化為性能圓βi圓的變化，如圖 5 所示，具有魯棒性的控制器設計區域縮小為陰影部分區域。

命題3 備注1假設被控對象內部的不確定性對Gi造成的乘積攝動為

β′i圓以Gi′(jω)為圓心，|為半徑，βsup為穩定裕度，當時，圖 5 中不存在魯棒控制器設計區域。

命題4（控制綜合問題）設計點α(jω)的復平面坐標可通過式（19）來構造相應控制器：

并可根據實際需求進一步實現控制器K的數學表達式，如傳遞函數表達式等。

命題4 備注1可以通過如下的構造法［18］，將設計點α(jω)的復平面坐標轉化為強鎮定控制器傳遞函數表達式K（s），使得K（s）在頻率ω下的表達式K(jω)滿足式（19）。

假設設計點α(jω) 對應的靈敏度函數S(jω)=α(jω)-1=a+bj，a和b同號，以下分別從同正和同負為例進行構造。

1）a、b均為正數

2）a、b均為負數

定義，同理可構造

式中：

其中：A＞0，c＜0，d＞0。相應的強鎮定控制器傳遞函數形式表示為

式中：σ是一個小的正數，用于將控制器的極點移到左半平面，σ越小，K（s）在設計頻率ω處越近似于K(jω)。

a和b一正一負的2 種情況可同理進行構造。若構造出的傳遞函數階數較大，可進行降階處理。

命題4 備注2對于在有限頻域[ω1，ω2]內求解控制器K的問題，可以通過如下簡化方式進行設計：

1） 在[ω1，ω2]取N個頻率點，在圖 3（a）所示控制器設計區域中依據命題2 選取合適的設計點α，分別采用命題4 備注1 的方法構造對應的控制器Kp，p=1，2，…，N并實現。

2） 比較不同單頻控制器傳遞函數在有限頻帶[ω1，ω2]上的頻率特性，選擇頻率特性最優的單頻控制器作為有限頻帶[ω1，ω2]內的控制器K。

命題5（不同控制器抗擾性能對比問題）對于給定輸入輸出傳遞函數類控制器K（s），可以得到K（s）在特定頻率ω下對應的復平面點α(jω)表達式：

命題5 備注1通過幾何圖示可以直觀地比較不同輸入輸出傳遞函數類控制器（例如PID 控制器、混合靈敏度H∞控制器等）的抗擾性能，如圖 6 所示，和分別表示不同控制器K（s）所對應的復平面點，不同控制器作用下閉環系統各輸出量的抗擾性能可根據式（15）的原理直觀地從幾何圖上得到。

3 GDM 抗擾控制器性能仿真分析

本節針對第1 節定義的發動機典型抗擾問題，對巡航穩態工況下GTF 發動機的抗擾控制器進行設計及仿真驗證。抗擾控制器設計及仿真分析流程的總結如圖 7 所示。

3. 1 GTF 巡航點鄰域帶干擾影響的線性模型

GDM 控制器需要基于發動機的線性化模型進行設計。基于2.1 節介紹的GTF 發動機部件級模型，采用小擾動辨識法得到巡航包線內某穩態工作點（H=28 000 ft，Ma=0.73， PLA=83.4°，1 ft=0.304 8 m）鄰域的傳遞函數矩陣模型為

式中：

式中：Nfc、F、Wf和Ma分別代表歸一化風扇折合轉速、推力、燃油流量以及馬赫數干擾的增量。

3. 2 干擾量對輸出量的傳遞函數頻域分析

干擾量的頻率特性研究是GDM 抗擾控制器設計的關鍵。分析馬赫數干擾對轉速和推力的開環頻率響應如圖 8 所示。可以看出，在0～10 rad/s 內，轉速和推力幅頻特性變化基本一致；但10～100 rad/s 內，對于該頻率段下的干擾信號，轉速的波動將呈現較大的衰減，但推力波動沒有。對于100 rad/s 后的干擾，2 者的波動均呈現較大衰減，有較強的濾波能力。根據文獻［19-20］提出的大氣湍流干擾模型的原理，可以取諧波輸入信號為

將得到的歸一化輸入馬赫數干擾信號進行傅里葉變換，如圖9 所示。結合圖 8 和圖 9，本文選取ω在2～16 rad/s 的有限頻域進行抗擾控制器的設計研究。

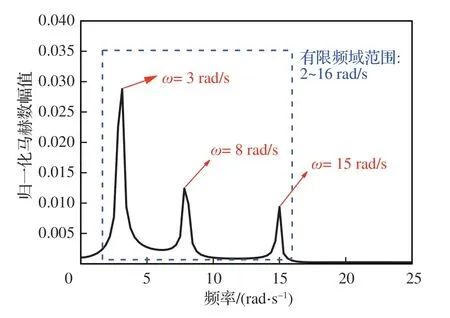
圖9 歸一化馬赫數干擾的頻譜分析Fig. 9 Normalized Mach number disturbance spectrum

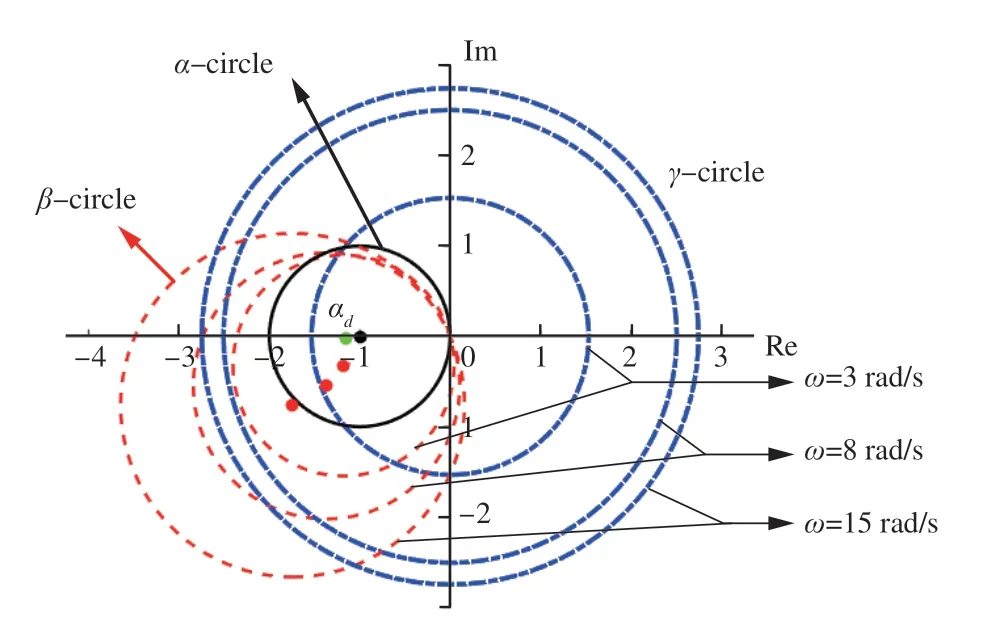
圖10 復平面上GDM 控制器設計區域Fig. 10 GDM controller design area on complex plane

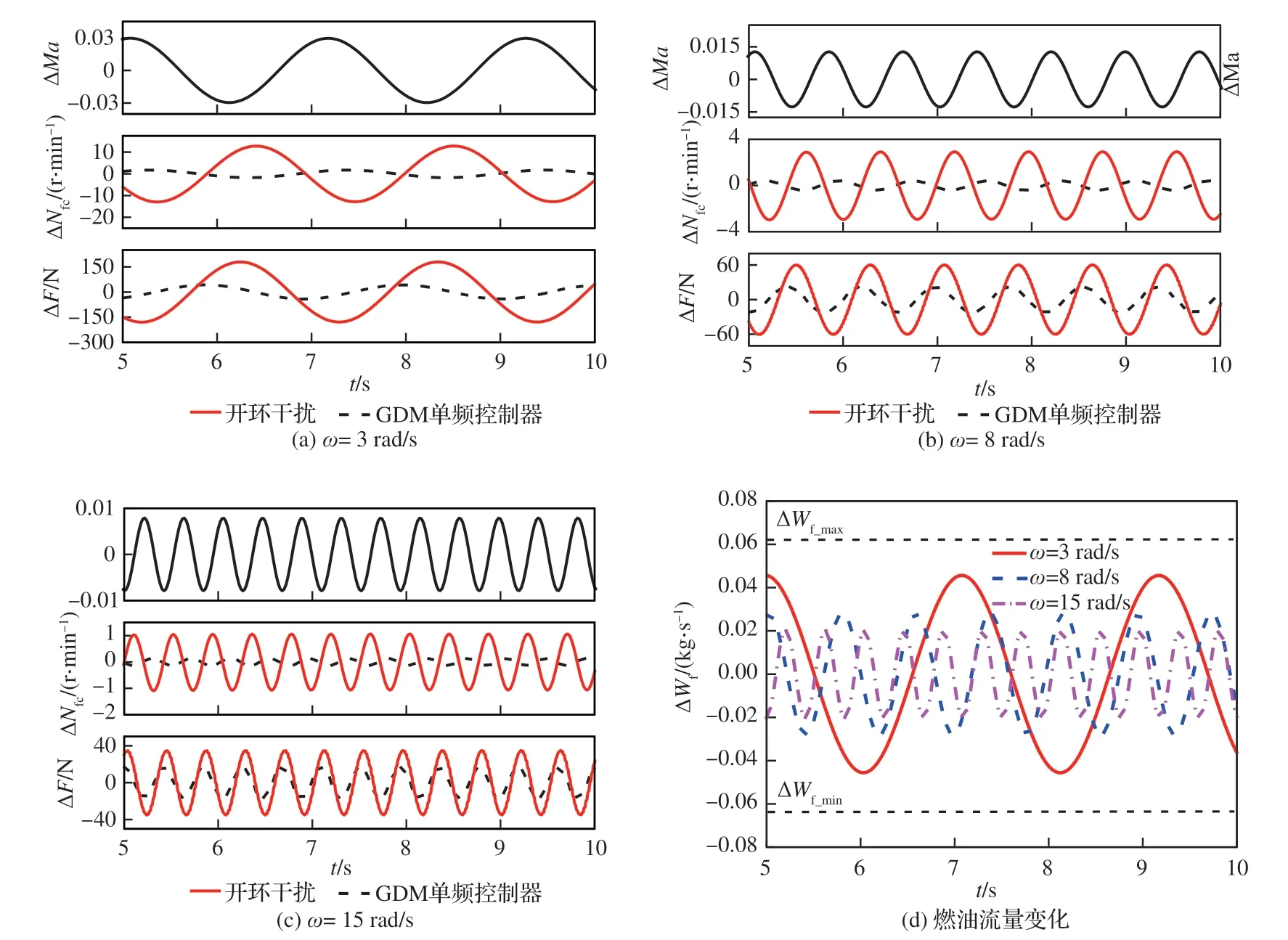
圖11 不同頻率下GDM 單頻控制器的抗擾性能Fig. 11 Disturbance rejection performance of GDM controller under different single frequency

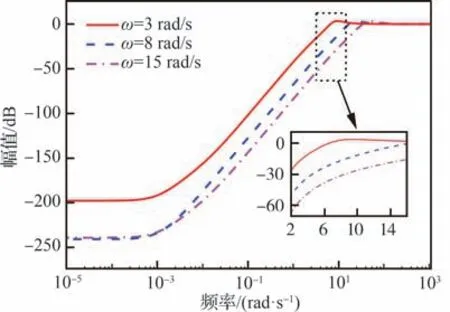
圖12 不同GDM 單頻控制器作用下ηyd 在有限頻域的幅頻特性Fig. 12 Comparison of ηyd frequency domain characteristics among different GDM controllers

3. 3 GDM 抗擾控制器設計及抗擾性能驗證

首先進行單頻抗擾控制器設計。根據命題1，分別在頻率點3、8、15 rad/s 處在復平面上進行幾何分析，并根據命題3 和命題4 選取合適的α點進行次優控制器實現，如圖 10 所示。

根據命題2 分析圖 10 可得，在α圓心左側且位于3 個頻率下所有圓交集區域內取設計點，可以得到全局抗擾性能較好的次優控制器。以設計點α坐標為（-1.15，-0.02）為例，由式（15）可得設計點不同頻率下對應不同輸出量的設計抗擾性能指標，如表 1 所示。

為驗證表 1 直觀在圖 10 中得到的各輸出量抗擾性能指標的準確性，在時域中進行仿真算例如下。首先，根據命題4 傳遞函數構造法實現相應GDM 控制器并統一降階至易于實際使用的三階，假設在單位正弦馬赫數干擾作用的情況下，各頻率下GDM 控制器的閉環系統輸出擾動量如圖 11 所示。降階后不同頻率下各GDM 控制器傳遞函數以及從圖 11 得到的實際抗擾性能匯總在表 2。可以看出，降階后GDM 控制器傳遞函數在各自設計頻率下所對應的α(jω)略有偏差，實際抗擾性能基本達到表 1 從圖 10 上直觀得到的設計抗擾性能指標；從圖 11（d）可以看出圖 10 中的限制圓也有效地限制住了由于抗擾控制器的引入所帶來的燃油流量的變化。仿真結果初步驗證了理想抗擾控制器設計方法的特征1～特征3。

其次，進行有限頻域內抗擾控制器設計。選擇由式（28）所示諧波信號作為大氣湍流干擾模型的輸入得到的馬赫數干擾信號，來作為發動機模型的干擾輸入，從圖 9 可知，馬赫數干擾能量集中在有限頻域2～16 rad/s。比較不同GDM 單頻控制器在有限頻域下的控制性能指標ηyd和ηzd的頻率特性，分別如圖 12 和圖 13 所示。由圖 12 可見，ω=15 rad/s 的控制器在有限頻域2～16 rad/s 相比其他2 個單頻控制器具有更好的折合轉速抗擾控制性能。由圖13 可見，各個單頻控制器在設計頻率前具有較好的抗擾性能，但在設計頻率之后抗擾性能開始快速惡化，這符合幾何設計法的原理，考慮在2～16 rad/s 的頻率段確定綜合被控量和性能量抗擾性能最佳的控制器，初步選擇在ω=15 rad/s設計的單頻控制器作為GDM 寬頻控制器。為進行進一步驗證，不同單頻控制器在時域下抗擾性能仿真驗證結果如圖14 和圖15 所示。

表1 不同頻率下控制器設計點所對應的性能指標ηyd 和ηzdTable 1 Design ηyd and ηzd under different single frequency

表2 不同頻率下GDM 控制器傳遞函數實現形式及所對應的實際抗擾性能Table 2 Realistic performances and transfer functions designed by GDM under different single frequency

表3 不同GDM 單頻控制器在時域下穩態抗擾性能對比Table 3 Comparison of disturbance rejection performances among GDM controllers designed in different frequency

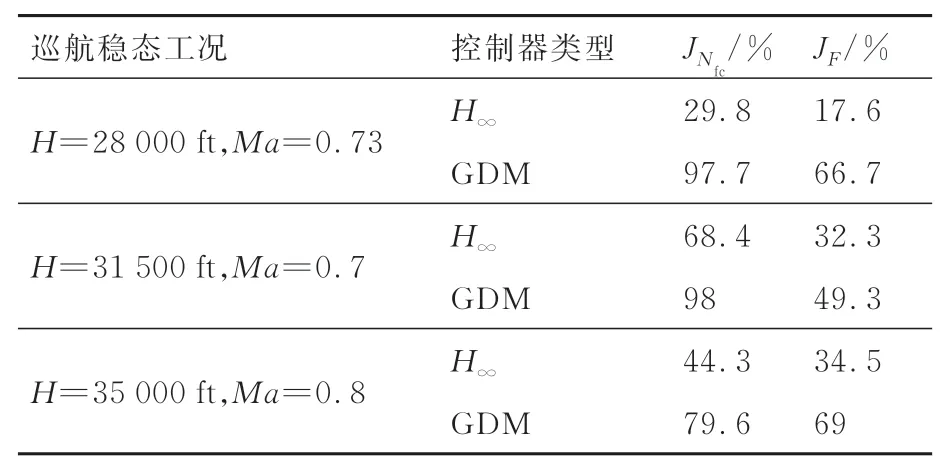
表4 不同巡航穩態工況下穩態控制器的抗擾性能比較Table 4 Comparison of controller disturbance rejection performance under different cruise steady-state points

圖13 不同GDM 單頻控制器作用下ηzd 在有限頻域的幅頻特性Fig. 13 Comparison of ηzd frequency domain characteristics among different GDM controllers

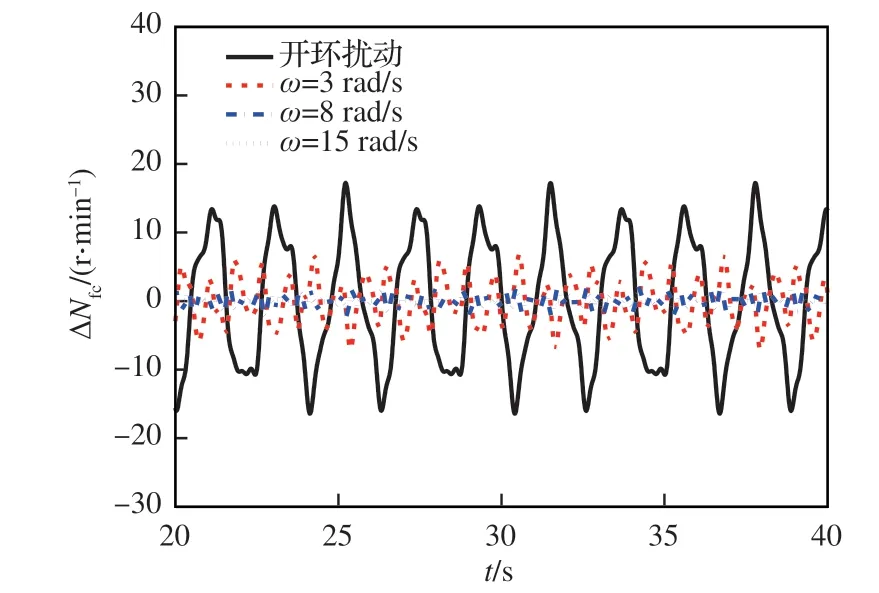
圖14 不同GDM 單頻控制器作用下風扇折合轉速的穩態擾動性能變化Fig. 14 Time domain characteristics of corrected fan speed under different GDM controllers

圖15 不同GDM 單頻控制器作用下推力的穩態擾動性能變化Fig. 15 Time domain characteristics of thrust under different GDM controllers

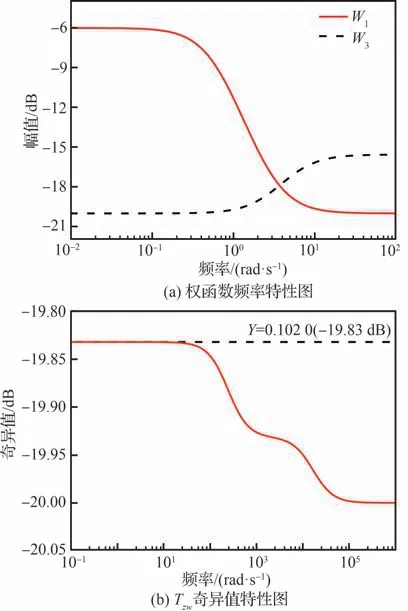
圖16 混合靈敏度H∞控制器權函數及Tzw的頻率特性Fig. 16 Frequency characteristics of weight function and Tzw in mixed sensitivity H∞ controller

為了更好定量地在時域下評估不同控制器的抗擾性能，定義性能量抗擾百分比J為

式中：qc_max和qo_max分別為相同干擾輸入時，閉環控制器作用下與開環作用下輸出量的最大擾動量。各GDM 單頻控制器閉環作用下對被控量折合轉速Nfc和性能量推力F的抗擾性能定量結果如表 3 所示。仿真結果表明，ω=15 rad/s 設計的單頻控制器具有接近性能極限的折合轉速抗擾百分比以及最高的推力抗擾百分比，可作為最終選定的GDM 控制器用于GTF 發動機巡航工況下馬赫數干擾的有限頻域抗擾控制器。

3. 4 混合靈敏度H∞與GDM 控制器有限頻域抗擾性能對比

采用3.3 節設計的GDM 控制器與發動機常用的混合靈敏度H∞控制器進行有限頻域抗擾性能對比。混合靈敏度H∞控制器設計過程參考文獻［2］，定義在全頻域的閉環傳遞函數的H∞指標為

混合靈敏度加權函數W1和W3構造過程為

式中：εα和εS為加權靈敏度函數矩陣的調節因子；εβ和εT為加權補靈敏度函數矩陣的調節因子；ωB為閉環系統設計帶寬。 本研究中取ωB=3 rad/s，εS=0.2，εT=0.2，εα=0.1，εβ=0.1。通過求解式（30）的次優H∞問題，可以得到p為0.102 0，加權函數的頻率特性圖以及Tzw的奇異值特性如圖 16 所示。可以看出，混合靈敏度H∞控制器使得Tzw的H∞范數指標在全頻域范圍內小于0.102 0（-19.83 dB），保證了全頻域范圍內的抗擾性能，但在有限頻域抗擾問題上具有一定的保守性。

對比混合靈敏度H∞和GDM 控制器抗擾性能指標ηyd和ηzd的頻率特性，如圖17 和圖18 所示。可以看出，GDM 控制器即便在其他部分頻域段的系統抗擾性能不如混合靈敏度H∞控制器，但在發動機巡航抗擾所關注的有限頻帶2～16 rad/s 上，GDM 控制器作用下系統的抗擾性能得到顯著提升。

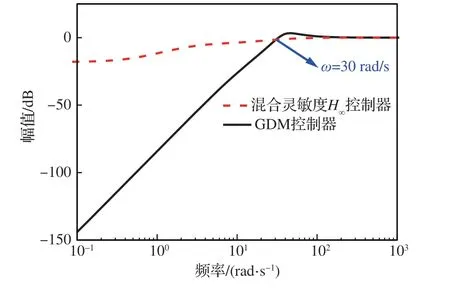
圖17 混合靈敏度H∞與GDM 控制器作用下ηyd 在有限頻域的幅頻特性Fig. 17 Comparison of ηyd frequency domain characteristics between H∞ and GDM controller

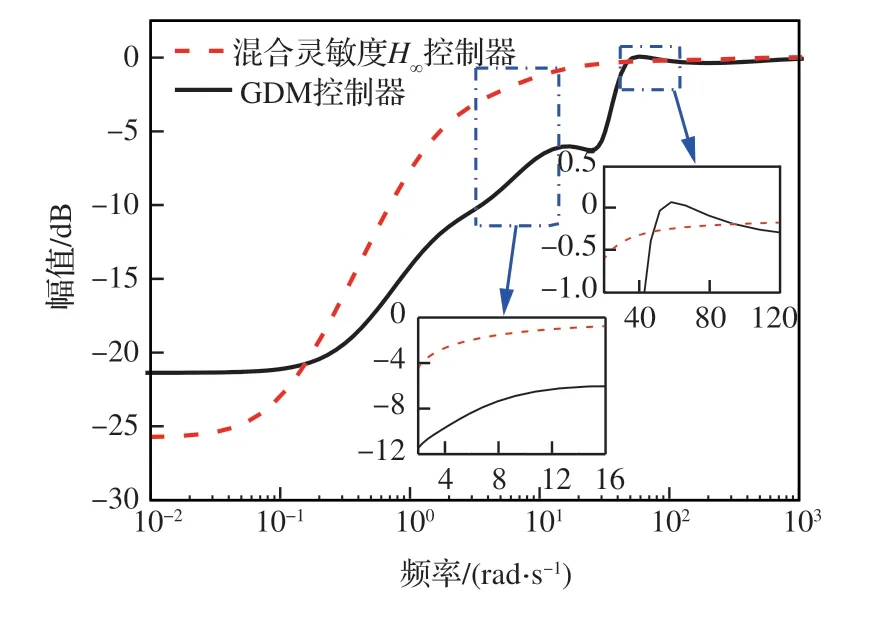
圖18 混合靈敏度H∞與GDM 控制器作用下ηzd 在有限頻域的幅頻特性Fig. 18 Comparison of ηzd frequency domain characteristics between H∞ and GDM controller

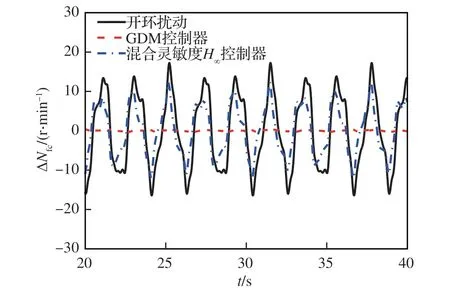
圖19 混合靈敏度H∞與GDM 控制器作用下風扇折合轉速的穩態擾動性能變化Fig. 19 Time domain characteristics of corrected fan speed under H∞ and GDM controllers

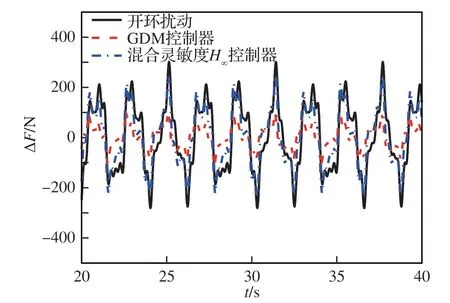
圖20 混合靈敏度H∞與GDM 控制器作用下推力的穩態擾動性能變化Fig. 20 Time domain characteristics of thrust under H∞ and GDM controller

在相同馬赫數干擾作用下，混合靈敏度H∞控制器和GDM 控制器的抗擾仿真驗證結果如圖 19 和圖 20 所示。混合靈敏度H∞控制器的Nfc抗擾百分比和F抗擾百分比分別為29.8% 和17.6%，遠小于表 2 中GDM 控制器97.7%的Nfc抗擾百分比和66.7%的F抗擾百分比，論證了頻率特性圖 16 和圖 17 分析結果的準確性。

為進一步驗證該GDM 抗擾控制器的設計流程的適用性，另取GTF 發動機巡航包線下2 個穩態工況點，采用圖 7 的設計流程進行抗擾控制器設計，結果如表 4 所示。可以看出，采用幾何設計法設計的抗擾控制器相比混合靈敏度H∞控制器，風扇折合轉速抗擾百分比提升30%以上的同時，推力抗擾百分比提升了15%以上，全局抗擾性能有顯著提高，基于幾何設計法的穩態抗擾控制器具有普遍適用性。

4 結 論

首先建立大涵道比齒輪傳動渦扇發動機部件級模型，針對傳統的混合靈敏度H∞抗擾控制方法缺少在控制需求指定頻率ω0或有限頻域[ω1，ω2]上定義出性能極限的能力，提出了一種可以在任何關注頻率或有限頻域上進行性能改進的通用方法“幾何設計法”，定義出基于幾何設計法的航空發動機抗擾控制器設計路線，為航空發動機穩態抗擾控制器的設計提供了一種新的思路方法和方向，并在頻域和時域上進行了分析和仿真驗證，結果表明：

1） 幾何設計法相較于傳統抗擾控制器設計方法，通過參數的轉化代換從而使控制器選取范圍在復平面坐標系中體現為圓的交集，具有直觀性。可以滿足理想的發動機抗擾控制器設計方法應具備的特征。

2） 針對擾動分量集中在ω∈[2，16] rad/s 的有限頻域馬赫數干擾，由于幾何設計法的抗擾控制原理相較于混合靈敏度H∞控制更直觀地定義了特定頻率和有限頻域內控制器對閉環系統輸出量的抗擾性能，采用幾何設計法設計的抗擾控制器相比混合靈敏度H∞控制器，折合轉速抗擾百分比和推力抗擾百分比均有顯著提高。