地形模型的尺度對山區(qū)橋址區(qū)風特性的影響

侯濤 劉妍妍

數(shù)值模擬是研究復雜山區(qū)風特性的重要方法之一。為了研究地形模型的尺度對山區(qū)橋址區(qū)風特性的影響，以西部山區(qū)某大跨度懸索橋橋址區(qū)為工程背景，建立了以橋位為中心的50 km×50 km的大尺度模型和10 km×10 km的小尺度模型，采用CFD數(shù)值模擬的方法，研究了地形模型的尺度對橋址區(qū)平均風速和風向角的影響。結果表明：地形模型的尺度對橋址區(qū)平均風速的影響十分顯著。當來流由小尺度地形模型邊界輸入時，地勢平坦，氣流沿河道吹來，橋位上游的風向與入口風向基本平行，橋位風速較高。而當來流由大尺度地形模型邊界輸入時，由于山體的阻擋，橋位上游的來流風向近似平行于峽谷走向，橋位處風速明顯減小，跨中減小幅度約為25%。2種模型在橋位處的氣流流向相似，地形模型的尺度對橋位處的風向角的影響相對較小。

復雜山區(qū)； 風特性； 數(shù)值模擬； 尺度效應； 橋址區(qū)

U442.4 A

［定稿日期］2022-02-22

［作者簡介］侯濤（1982—），男，碩士，副教授，研究方向為市政、橋梁、城市軌道設計與施工; 劉妍妍（1987—），女，碩士，工程師，研究方向為結構工程。

風致災害在自然界中十分普遍。大跨度橋梁的柔度較大，在風荷載作用下易出現(xiàn)對結構不利的振動，抗風設計已成為大跨度橋梁設計的重要控制因素之一，而精確地獲取橋址區(qū)的風特性是抗風設計研究的前提。

研究深切峽谷橋址區(qū)風特性主要有3種手段：現(xiàn)場實測、風洞試驗和數(shù)值模擬。其中數(shù)值模擬與現(xiàn)場實測和風洞試驗相比，在研究費用、時間等方面均具有優(yōu)勢，且具有可視化的優(yōu)點。隨著數(shù)值求解方法的發(fā)展和計算機性能的進步，數(shù)值模擬方法已逐步成為研究復雜地形風特性的的重要手段。胡朋［1］建立了理想峽谷的CFD數(shù)值模型，研究了不同峽谷夾角和不同峽谷高度下的平均風特性和脈動風速譜。Huang和Zhang［2］采用k-ω SST湍流模型對香港小蠔灣附近的風特性進行了研究，數(shù)值模擬結果與現(xiàn)場實測和風洞試驗吻合良好。Maurizi等［3］建立了15 km×14 km的數(shù)值模型，采用k-ε湍流模型研究了近地風場，對比分析了網(wǎng)格尺寸及邊界條件對風剖面的影響。Uchida和Ohya［4］采用大渦模擬的方法對9.5 km×5 km范圍內(nèi)的風場進行了模擬，并對其加速效應與流動分離進行了分析。

雖然利用數(shù)值模擬的方法研究山區(qū)風特性已經(jīng)得到了廣泛的應用，但是對于計算區(qū)域的選取并無明確的標準，且對地形模型的尺度效應研究較少。模擬中若選取的計算區(qū)域太小，則難以保證風場的充分發(fā)展，進而無法真實地反映橋址區(qū)的風特性。但是若計算區(qū)域過大，對計算機的性能又有很高的要求。目前的研究中對地形范圍的選取比較任意，大多小于500 km2的地形范圍，胡峰強［5］建立了以北盤江大橋為中心半徑為2.4 km的數(shù)值模型，靖洪淼等［6］選取了以橋位為中心半徑為5 km的圓形地形，祝志文等［7］選取了以烏江大橋為中心的6 m×10 km的地形范圍，Nomura等［8］選取了以橋位為中心的8 km×8 km的地形范圍，薛亞飛和劉志文［9］選取了以山西臨猗黃河大橋為中心的10.8 km×9.0 km的地形范圍。

本文以西部山區(qū)某大跨度懸索橋橋址區(qū)為工程背景，分別建立了以橋位為中心的50 km×50 km的大尺度模型和10 km×10 km的小尺度模型，采用CFD數(shù)值模擬的方法進行對比分析，研究地形模型的尺度對橋址區(qū)平均風特性的影響，可為復雜山區(qū)風特性數(shù)值的計算區(qū)域選取提供參考。

1 工程背景

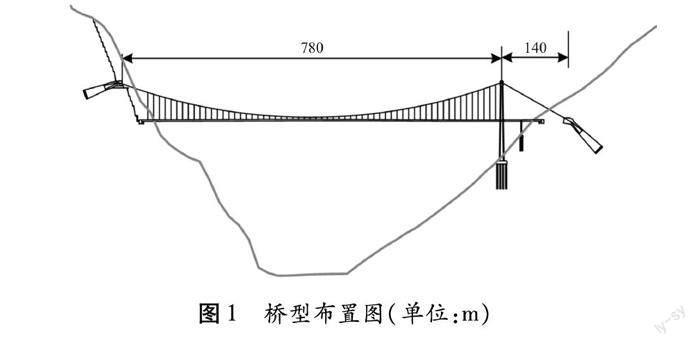
某大跨度懸索橋為單塔單跨形式，主跨780 m。橋型布置如圖1所示。橋址區(qū)群山環(huán)繞、層巒疊嶂、溝壑縱橫、支流繁復，屬于典型的山區(qū)峽谷地形，如圖2所示。橋位上游和橋位處的河道發(fā)生連續(xù)大角度彎曲。總體而言，該橋位處地勢起伏較大，地形狹窄，橋址區(qū)特有的復雜地形地貌對風特性可能產(chǎn)生較大影響。

2 數(shù)值模型

2.1 計算域的選取

本文選定以橋位為中心的50 km×50 km地形范圍進行研究，計算區(qū)域投影面積達2 500 km2，遠遠超出之前的研究范圍，可以更充分地考察橋址區(qū)的平均風特性。為了使計算域內(nèi)的氣流有充分的空間自由發(fā)展，避免邊界效應帶來的氣流壓縮，計算區(qū)域頂部高程設為10 000 m，滿足計算要求。同時，還建立了以橋位為中心的10 km×10 km的模型進行對比分析，研究地形模型的尺度對橋址區(qū)平均風特性的影響。

2.2 網(wǎng)格劃分

首先提取橋址區(qū)附近50 km×50 km范圍內(nèi)的高程信息，并對高程進行插值處理，生成三維地形點云，分辨率為100 m。對生成的三維地形點云曲面擬合后進行網(wǎng)格劃分。為了保證網(wǎng)格質(zhì)量，劃分時均采用六面體結構化網(wǎng)格。在高度方向，由于主要研究的是橋面高度以下的平均風特性，所以在網(wǎng)格劃分時距離地形表面越近網(wǎng)格越密，而海拔越高則越稀疏，首層網(wǎng)格高度為10 m。劃分好的網(wǎng)格如圖3所示，大尺度模型和小尺度模型計算區(qū)域最終共劃分的網(wǎng)格總數(shù)分別為4 732 000和700 000。

2.3 邊界條件

計算區(qū)域底面，即地形表面設置為無滑移壁面，頂面設置為對稱邊界；入口和出口邊界分別設置為速度入口和壓力出口。通過編譯UDF將入口風速沿高度方向分段輸入。在大氣邊界層內(nèi)，風速隨離地高度的增大而增大。偏安全地選用B類地表對應風剖面，所以地表粗糙度系數(shù)取為0.16。入口邊界最高海拔為2 289.4 m，最低點高程為1 091 m，所以大氣邊界層高程定為2 639.4 m，梯度風高度為1 548.4 m。海拔2 639.4 m以下入口風速按照B類地表指數(shù)規(guī)律分布；當海拔超過2 369.4 m，風速不再受地面粗糙度的影響，達到梯度風速，設為50 m/s。風速分布如圖4所示，跨中橋面高程為1 570 m，對應橋面高度處入口風速為41.4 m/s。

對于復雜山區(qū)地形下的橋梁抗風問題更關注其平均風特性，因此本文采用基于壓力的穩(wěn)態(tài)求解器進行計算。選用對流動分離具有較好解析度的SST k-ω湍流模型，采用二階格式離散控制方程，應用SIMPLE算法解決N-S方程中壓力-速度的耦合問題，對壓力、動量方程、湍流耗散率和湍動能方程采用二階迎風格式進行離散。

2.4 工況設置

復雜山區(qū)地形對風速的影響十分顯著，風速、風向具有明顯的區(qū)域特征。實際情況中，對橋梁抗風穩(wěn)定性影響最大的是橫橋向來流，橋址區(qū)的主導風向與橋軸線也接近垂直。因此，選取與橋軸線垂直的風向作為本研究的來流風向，如圖5所示。

3 計算結果

風速和風向角是影響橋梁抗風穩(wěn)定性最重要的參數(shù)。為了得到風特性沿橋軸線的分布，由西岸到東岸每1/8橋跨長度設置一個風速監(jiān)測點，共9個。為了研究風速沿海拔高度的變化，分別在1/4跨、跨中、3/4跨沿高度方向設置了20個監(jiān)測點，監(jiān)測點覆蓋了谷底至高空的1 400～1 500 m的海拔范圍。1/4跨、跨中、3/4跨3組監(jiān)測點的最低海拔分別為1 367 m、1 270 m和1 360 m。通過計算得到各風速測點的風速值，其中橫橋向風速和順橋向風速分別用u和v表示，風向角β的定義如式（1）所示。風向角正值代表來流從西吹向東，為負則代表來流從東吹向西。

β=tan-1v|u|（1）

3.1 風向角

圖6給出了橋面高度水平剖面風向角的分布。從圖6中可以看出，當來流由10 km×10 km的數(shù)值模型邊界輸入時，氣流沿河道吹來，未受到明顯的山體遮擋，來流運動軌跡與山勢起伏接近，橋位上游的風向與入口風向基本平行，如圖6（a）所示。當氣流經(jīng)過彎曲的河道、到達橋位處時，風向也僅發(fā)生了微小的變化，而經(jīng)過橋位后流線四處分散。風向角沿豎向和橋跨方向的分布如圖7所示。由于氣流由西北方向吹來，所以風向角為正。風向角沿豎向分布呈“S”型，在橋面高度處較大；沿橋跨方向呈現(xiàn)兩岸大、跨中小的趨勢，且在跨中分布較均勻。

而對于大尺度模型來說，即來流由50 km×50 km的數(shù)值模型邊界輸入時，橋址區(qū)的風環(huán)境發(fā)生了改變。由于西側存在連綿的山體，當來流充分發(fā)展流動至橋位上游處時，氣流已經(jīng)抬升至一定高度，再加上河道的改向，橋位上游的來流風向發(fā)生改變，不再與入口風向平行，而是近似平行于峽谷和河流走向，如圖6（b）所示。氣流由山頂向下俯沖至橋位，而后再匯集灌入下游河道中。來流經(jīng)過橋位后，沿著河道向下游流動，流動較集中。

與小尺度模型計算相比，風向角沿豎向總體呈現(xiàn)減小的趨勢。風向角在高空略有減小，但變化趨勢保持一致；在近地面變化較大，而橋面高度處的影響最小。風向角沿跨向分布與小尺度計算結果相差不大，僅在左岸有所差異，這是由于橋梁左跨與隧道相連，監(jiān)測點與山體距離很小，此處風速很小，輕微的擾動便會造成風向角的大幅度改變。風向角沿跨向由西岸向東岸單調(diào)遞增，風向角均為正，如圖7所示。

3.2 風速

圖8給出了橋面高度處水平剖面的風速云圖。當來流由10 km×10 km的數(shù)值模型邊界輸入時，來流沿河道吹來，地勢較平坦，未受到明顯的山體遮擋，橋位上游的風速較高，為40 m/s左右。來流經(jīng)過河道彎曲地帶時，受到山體的阻礙，風速有所降低。但是氣流進入峽谷到達橋位處時，由于空氣質(zhì)量不能大量堆積，于是加速流過峽谷，風速又增大，如圖8（a）所示，存在典型的“狹管效應”。圖9給出了監(jiān)測點風速沿豎向和橋跨方向的分布，風速沿高度的變化規(guī)律基本符合指數(shù)增長形式；風速沿橋跨方向呈現(xiàn)非均勻分布，靠近東西兩岸的風速較低，尤其是西側直接與隧道相接，風速接近于0，而跨中區(qū)域的風速較高，約為41.65 m/s，與風速入口橋面高度處風速接近。

而來流由50 km×50 km的數(shù)值模型邊界輸入，當來流充分發(fā)展流動至橋位上游處時，由于西側山體的阻擋，風速較入口風速有了明顯的減小，約為30 m/s，如圖8（b）所示。來流先攀升至東側的山體，再由山頂向下俯沖至橋位，而后再匯集灌入下游河道中。風速沿高度方向的剖面形狀發(fā)生了變化，風剖面系數(shù)減小。在3/4跨位置處，低空不再完全符合對數(shù)或指數(shù)形式，而是在一定高度范圍內(nèi)加速，呈“S”型，如圖9（a）所示。風速沿橋跨方向也發(fā)生了變化，與小尺度模型計算結果相比，風速大小明顯降低，跨中風速降低了約25.4%。除風速很小的西岸監(jiān)測點外，其余位置處的風速分布較均勻，如圖9（b）所示。

綜上所述，地形模型的尺度對復雜山區(qū)橋址區(qū)的風特性影響不容忽視，尤其是對風速的影響最大，而對橋位處風向角的影響相對較小。

4 結論

（1）當來流由小尺度地形模型邊界輸入時，橋位上游的風向與入口風向基本平行，而當采用大尺度模型后，橋位上游的來流風向近似平行于峽谷走向。而經(jīng)過彎曲的河道達到橋位處時氣流流向相似。

（2）風向角沿豎向分布呈“S”型，在橋面高度處較大。地形尺度大小對橋位處風向角的影響不明顯，僅在風速較小的左岸差異較大，而在跨中區(qū)域影響較小。

（3）當來流由小尺度模型邊界輸入時，氣流沿河道吹來，地勢平坦，橋位風速較高，接近入口橋面高度的風速。而當考慮大尺度模型后，由于山體的阻擋，橋位處風速明顯減小，減小幅度約為25%。

（4）對于小尺度模型，風速沿高度的變化規(guī)律基本符合指數(shù)增長形式；而對于大尺度模型，風剖面系數(shù)減小。在3/4跨，低空不再完全符合對數(shù)或指數(shù)形式，而是在一定高度范圍內(nèi)加速，呈“S”型。

參考文獻

［1］ 胡朋. 深切峽谷橋址區(qū)風特性風洞試驗及CFD研究［D］. 成都： 西南交通大學， 2013.

［2］ Huang W， Zhang X. Wind field simulation over complex terrain under different inflow wind directions［J］. Wind and Structures. 2019， 28（4）： 239-253.

［3］ Maurizi A， Palma J M L M， Castro F A. Numerical simulation of the atmospheric flow in a mountainous region of the North of Portugal［J］. Journal of Wind Engineering and Industrial Aerodynamics. 1998， 74-76： 219-228.

［4］ Uchida T， Ohya Y. Large-eddy simulation of turbulent airflow over complex terrain［J］. Journal of Wind Engineering & Industrial Aerodynamics. 2003， 91（1）： 219-229.

［5］ 胡峰強. 山區(qū)風特性參數(shù)及鋼桁架懸索橋顫振穩(wěn)定性研究［D］. 上海： 同濟大學， 2006.

［6］ 靖洪淼，廖海黎，周強，等. 一種山區(qū)峽谷橋址區(qū)風場特性數(shù)值模擬方法［J］. 振動與沖擊. 2019， 38（16）： 200-207.

［7］ 祝志文，張士寧，劉震卿，等. 橋址峽谷地貌風場特性的CFD模擬［J］. 湖南大學學報（自然科學版）. 2011， 38（10）： 13-17.

［8］ Nomura T. Prediction of large-scale wind field over complex terrain by finite element method［J］. Journal of Wind Engineering and Industrial Aerodynamics. 1997， 67-68： 947-948.

［9］ 薛亞飛，劉志文. 復雜地形橋位風場空間分布特性數(shù)值模擬［J］. 公路交通科技. 2016， 33（5）： 66-72.