異質日變交通流下路網施工影響研究

黃曉平

摘要 文章闡述異質日變交通流概念，從數理模型、計算過程兩方面介紹異質日變交通流分析模型要點，并圍繞算例，就路網維修施工的工程隊數量配置和工期配置狀態對優化施工順序的影響開展了模擬分析，希望該分析方法及相關分析成果能對城市路網施工克服交通阻抗的工程應用提到一定的參考作用。

關鍵詞 路網；異質日變交通流；施工影響；分析模型

中圖分類號 U491文獻標識碼 A文章編號 2096-8949（2023）11-0039-03

0 引言

交通延誤是道路維修施工控制的不利影響之一，尤其對于人、車密集，交通繁忙的城市路網維修工程，加強工區交通流控制，降低工區阻抗，克服工區路網交通流延誤，一直是多方重視的工程管理課題[1]。異質日變交通流分析模型，以施工路網整體交通流為基礎，不考慮施工區的具體類別屬性、幾何形狀等特征，而通過計算不同施工組織方式下路網阻抗增量的關聯影響，探討施工組織狀態對路網交通流的影響關系。下文通過介紹異質日變交通流模型分析相關知識要點，并通過算例，分析該數理模型就路網施工順序對交通阻抗影響的分析過程及成果，以期為路網維修施工提供組織管理或決策參考。

1 異質日變交通流分析模型

首先，將施工路網上的過行者分為2類。

第一類：理性過行者，嚴格遵循最短路徑原則，在過行施工路網時，不會夸大施工對過行的影響，對路網阻抗認識不存在主觀偏差，是一種較為理想化的過行者狀態。此狀態利于模型分析的簡潔化引用，但不能充分反映過行交通流的實際狀態。

第二類：有限理性過行者，其對路網的最短過行距離的要求比較寬泛，認為只要在一定距離范圍內的路徑即可作為備選路徑，即：接受一個過行距離區間，只要路徑處于該區間之內，即為認可的優化過行路徑[2]。此外，在通過施工路網時還會夸大施工對過行的影響，對路網阻抗認識存在一定的主觀偏差。

模型分析中，交通流由上述兩類過行者混合構成，即為異質交通流。隨著施工進程的推進，交通流過行效率或過行路網阻抗逐日發生動態變化，形成日變交通流狀態。基于異質和日變的過行特征開展交通流模型分析，即為異質日變交通流模型分析。該模型即為異質日變交通流分析模型。

1.1 數理模型

異質日變交通流分析的數理模型，以施工路網總阻抗的增量之和為目標控制函數，以兩類過行者流量工期變化規則、流量守恒條件和最長工期為約束。相關函數、公式及參數項具體如下。

模型中，P（j）——由施工順序j所引起的路網總阻抗的增量；i——第i個作業段；ti——第i個作業段中的第t個工日；Ti——第i個作業段的工期；——第i個作業段第t個工日時區段總流量的分布向量；x0——施工前區段的流量向量；——施工前一類過行者的區段流量的分布向量；——施工前二類過行者的區段流量分布向量；TD——最長工期；c（x）——經BPR函數算得的區段阻抗向量；——第i個作業段中第t個工日時一類過行者的區段流量分布向量；——第i個作業段中第t個工日時二類過行者的區段流量分布向量；——OD對rs區間的交通條件需求，是個固定值；——在第i個作業段中第t個工日時，OD對連接rs區間k路徑的流量；——施工前OD對連接rs區間k路徑的流量；——如果區段a在OD對連接rs區間的k路徑上，則取值1，否則取值0。

目標函數（1）由兩部分構成，其第1部分代表在施工直接或間接影響時程內，過行者基于不同的過行規則引發的路網總阻抗；第2部分代表無施工條件下，過行者在同樣時程內所形成的路網總阻抗；二者差值即為區段作業所造成的路網阻抗的增量，由于過行者對路網最短路徑的認知存在閾值，使模型的平衡點不是表現為一個單一的平衡點，而是表現為一個集合。為便于計算，取UE平衡點為初始狀態。約束（2）代表工程影響條件下的異質交通流的變化狀態；約束（3）代表非施工條件下區段流量分布；約束（4）代表最長工期限制；約束（5）—約束（10）代表不同時程內路徑交通需求、路徑流量及區段流量之間的關系。上述約束是基于施工影響背景的對日變交通流分配模型的約束。

1.2 計算過程

求解計算過程如下：

（1）初始化，確定模型和遺傳計算方法中涉及的參數，即確定路網拓撲結構、初始種群數量、自由行駛時程、通行能力、OD對數量、交通需求、工區位置、過行比例、認知偏差系數、迭代運算步長、交叉概率、變異幾率以及迭代次數等[3]。

（2）以數字編碼的方式，產生與初始種群數量相匹配的初始可行解數量。

（3）計算可行解適應度函數，求解每天的流量演化

過程：①無施工配置狀態下路網的交通分布向量計算，而計算路網的總阻抗。②計算可行解對應的施工段存在施工影響下的通行能力分布矩陣。③根據所對應的過行能力分布矩陣，計算獲得理性過行者在第t+1工日的區段過行流量的分布向量。首先計算獲得理性過行者對t+1工日路網狀態的認知阻抗，其中在t>2條件時，阻抗取近3日的均值，其次計算獲得理性過行者在區段流量變化的向量；最后計算獲得理性過行者在t+1工日時的區段流量分布向量。④通過矩陣計算，獲得有限理性過行者在第t+1工日時的區段流量分布向量，首先計算獲得有限理性過行者對t+1工日時路網狀態的認知阻抗；其次計算獲得有限理性過行者對區段a第t+1工日時認知阻抗所存在的主觀認識偏差；計算獲得可接受線路的流量集合Ωf，取得可接受區段流量集合Ωx；在Ωx中計算獲得有限理性的過行者在第t+1工日時區段流量變化向量；取得有限理性過行者在第t+1工日時區段流量分布向量。⑤計算獲得第t+1工日時區段總流量分布向量。⑥由函數（1）獲得可行解適應度。⑦重復②—⑤步驟，獲得每一個可行解的解適應度。

（4）對收斂性進行狀態判斷。判斷迭代運算次數是否符合準則規定的迭代次數要求，如符合要求，則獲得優化解，終止計算過程；否則，進入下一步。

（5）獲得新可行解。遵循步驟（3）中所得的適應度，確定向下一代種群遺傳的個體，并給予變異和交叉操作，以適當增加多樣性解，從而獲得新可行解，返回步驟（3）。

2 算例情況簡介

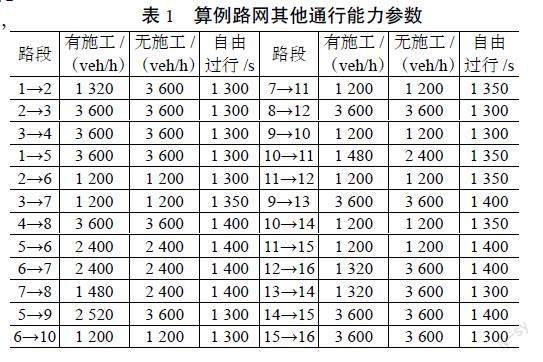
算例路網如圖1所示，路網呈現有向連接的網絡分布狀態，包括24個區段，16個節點，1個（1～16）OD對。路網設置施工區6個，分別位處6個區段。假定OD對1～16間的過行需求為6 500輛固定值，其他區段狀態信息參數見表1所示。表中自由過行時間單位取為s，作業前后，路網過行能力的數值單位取為輛/h。

3 路網施工順序影響分析

3.1 工程隊數量配置對優化施工順序的影響

應用前述介紹的異質日變交通流演化分析模型，圍繞工程隊數量配置對優化施工順序的影響問題進行仿真模擬分析。有限理性過行者的比例取η=0.50，路網只1個工程隊在施工時，無法將其最長工期TD限制在≤250 d，2個以上工程隊配置時均限制在≤250 d最長工期條件的一個重要參數。仿真模擬中，理性過行者的比例參數λ1、演化步長取α1、時程權重值γ1分別取為0.60、0.60、0.70；有限理性過行者的比例參數λ2、演化步長取α2、線路認知閾值系數δ、線路認知偏離系數φa分別取值0.50、0.10、0.10。

當路網上工程隊的數量按1～6個配置時，不同工程隊配置數量下的日變阻抗特征的分析結果顯示，路網上不同數量的工程隊配置，對應不同的施工順序。差異在于理性條件下，其交通日變演化整個過程比較平緩；而在理性過行者和有限理性過行者混合存在條件下，該演化過程則波動性比較大，是由于有限理性過行者帶來的阻抗變化影響[4]。當路網只有1～5個工程隊作業時，路網阻抗單日較小，帶來的交通壓力相對較小；而當工程隊配置數量提升到6個時，路網阻抗則單日較大，顯示6個工程隊同時投入作業時，會給路網交通帶來較大壓力，過行通行能力深受影響。

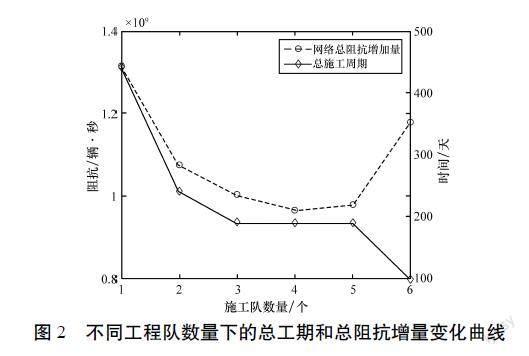
通過計算獲得路網不同工程隊數量下的總工期和總阻抗增量變化曲線如圖2所示。

圖2曲線顯示，在只以工程隊數量作為變量，以工程隊作業引起的路網總阻抗增量最低為控制目標的條件下，工程隊的數量增加并不一定帶來總工期縮短，如當路網上存在3個、4個、5個工程隊時，且每單位的總工期均為190 d，如果要滿足工程隊數量增加帶來縮短工期的要求，則還需進一步對總工期進行細化約束。另外當路網存在4個工程隊時，阻抗影響降到最低值；當路網存在3個工程隊和5個工程隊作業時，阻抗影響與4個工程隊時的差異并不大；當路網存在1個工程隊和6個工程隊時，阻抗影響則相對比較大。

3.2 工期配置狀態對優化施工順序的影響

在日變交通流分配模型下，為研究工期對阻抗日變特征和優化施工順序的影響，該研究也開展了相關模擬仿真分析。此分析中工程隊配置數量取2個，狀態1最長工期TD的限制為≤250 d，由于狀態2～9中各作業區的工期分別是狀態1的1.50倍、2.00倍、2.50倍、3.00倍、3.50倍、4.00倍、4.50倍、5.00倍。這里對狀態2～9的最長工期限制也取以狀態1的某個倍數，其他參數同前。

在施工順序安排上，9種施工配置狀態共存在5種施工順序，其中前4個施工配置狀態各存在1種施工順序，狀態5～6存在1種施工順序，狀態7～9存在1種施工順序。狀態9之后，該研究曾想繼續增加工期，但發現其不再影響改變施工順序。此種情況表明：存在一個工期閾值，特定閾值區間內，不會發生施工順序優化變化。不過在異質日變交通流條件下，工期閾值要比同質交通流要大一些。

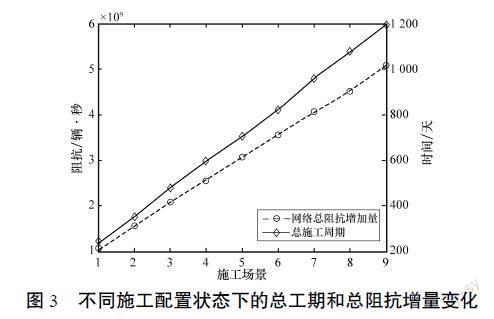
根據上述不同狀態下的施工甘特圖及日變路網阻抗，獲得不同施工配置狀態下的總工期和總阻抗增量變化如圖3所示，

隨著工期的增加，總工期及路網總阻抗增量基本上呈現線性增長發展態勢，是由于該研究對各個狀態下的最長工期約束采取了線性增加配置狀態，若不同施工配置狀態的總工期約束不是呈現線性發展狀態，則實際總工期及路網總阻抗增量的關系還需要進行模擬分析研究。

4 結語

該文就路網施工組織順序對路網交通阻抗的影響分析問題開展了技術研究。介紹了異質日變交通流模型分析相關概念，闡述了異質日變交通流分析數理模型及計算分析過程等主要知識點。并圍繞算例，應用該模型，就工程隊數量和工期配置對優化施工順序的影響，開展了應用分析研究。結果表明，異質日變交通流模型分析方法，對城市路網維修施工優化組織方式，降低工期路網阻抗，提高施工路網交通過行效率等具有實用參考意義。

參考文獻

[1]李青. 考慮有限理性的活動—出行配流模型研究[D]. 南京：南京大學， 2017.

[2]于新蓮. 考慮有限理性的交通流Day-to-day動態演化研究[D]. 南京：南京大學， 2014.

[3]潘曉鋒. 基于有限理性的方式劃分和交通分配組合模型[D]. 大連：大連理工大學， 2015.

[4]張璽， 趙新朋， 楊達， 等. 考慮出行者有限理性的日變交通分配模型[J]. 公路交通科技， 2018（7）： 93-99.