擴散型風力機葉片的優化設計

張子英，魯中間，高偉龍

(1. 山西能源學院機電工程系，太原 030006；2. 中國礦業大學(北京)機電與信息工程學院，北京 100083；3. 青島安華新元風能股份有限公司，青島 266000；4. 北方工程設計研究院有限公司，石家莊 050011)

0 引言

中國的風能資源豐富，碳達峰、碳中和目標的實施將為風電產業迎來更大的發展空間，鄉村振興戰略也為低風速地區小型風電場的發展帶來新的機遇。隨著“十四五”規劃、“千鄉萬村馭風行動”方案的落實，預計2023—2025 年鄉村振興類分散式離網型中小型風力機的開發和利用將異軍突起[1]。鑒于中國鄉村地區的風功率密度一般在100 W/m2以下，且年可利用時長小于3000 h[2]，擴散型風力機(diffuser augmented wind turbine，DAWT)的應用將具有明顯優勢。

擴散型風力機的結構示意圖如圖1 所示。擴散器將來流風濃縮、加速，以提高經過葉輪的風速，從而提升風電機組的輸出功率，實現了低速風能的高效利用，因此其又被稱為濃縮型風力機。

圖1 擴散型風力機的結構示意圖Fig. 1 Structure diagram of DAWT

國內的田德教授團隊在擴散型風力機領域開展了多年研究，主要是通過仿真[3-4]或者實驗[5-6]方法，研究不同擴散器結構內部的流場特性，分析擴散器的結構變化對風電機組輸出功率的影響，取得了一系列創新性成果。國外學者大多利用理論方法建立風力機流場模型來研究流場特性，以指導風力機的結構選型及參數設計。Vaz等[7]利用葉素-動量理論，提出了擴散型風力機的一維數學模型，基于軸對稱假設對風力機葉輪與擴散器進行耦合CFD 計算，以評估風力機的能量轉化性能。Benini 等[8]基于葉素理論建立了葉輪的氣動模型，采用進化計算方法對水平軸風力機的擴散器進行了優化設計。Paranjape 等[9]基于計算流體力學，通過求解二維非定常N-S 方程，研究了擴散器截面幾何形狀變化對風力機性能的影響。

綜上可見，目前國內外關于擴散型風力機的研究主要是分析擴散器的結構變化對風力機性能的影響。然而，葉片作為風力機獲能的核心構件，針對擴散器內部流場開展與之相匹配的葉片設計研究，是保障風力機獲能效率的另一個重要途徑。Vaz 等[10]提出了一種考慮尾流影響的水平軸風力機葉片截面弦長和扭轉角分布優化模型，該模型以風力機功率系數最大化為目標，考慮葉輪平面內軸向感應因子與尾流間的關系，實現了葉片截面弦長、扭轉角的優化設計。雖然該模型是針對一般水平軸風力機建立的，但該模型為多葉片葉輪的優化設計提供了一種簡單的替代工具，同樣適用于擴散型風力機。

本文基于葉素-動量理論和簡單的擴散器效率計算方法，將擴散器與風力機葉片設計理論相結合，建立了一種用于低風速場景的擴散型風力機模型。尋求更適用于擴散型風力機獲能特點的葉片設計方法，可為擴散型風力機的開發提供支持。該模型包含了風力機來流風速、葉輪平面處風速、擴散器出口風速、尾流風速、風力機葉片荷載、葉素參數及風能利用系數之間的關聯關系。針對某型號擴散型風力機，利用該模型開展葉片結構參數的優化設計，并通過Fluent 軟件對優化設計前、后的風力機流場進行仿真模擬分析。

1 基于葉素-動量理論的擴散型風力機氣動分析模型

擴散型風力機的氣動原理示意圖如圖2所示。圖中：0 為來流；1、2 分別為葉輪的迎風面和背風面；3 為擴散器出口平面；4 為風力機的下游；V0為外界及風力機擴散器進口位置處的來流風速，m/s；V1、V2均為葉輪平面處風速，m/s，本文近似看成V2=V1；V3為擴散器出口風速，m/s；V4為尾流風速，m/s；r為葉素徑向位置，即葉素半徑，m；dr為葉片微元段；R為葉片長度，即風力機葉輪半徑，m；u1為不帶擴散器的普通風力機的尾流風速，m/s。本文假設在擴散器出口處的輸出條件與不帶擴散器的普通風力機的輸出條件相同，即沒有額外的背壓，u1為下游風速，則V4=u1[7]。

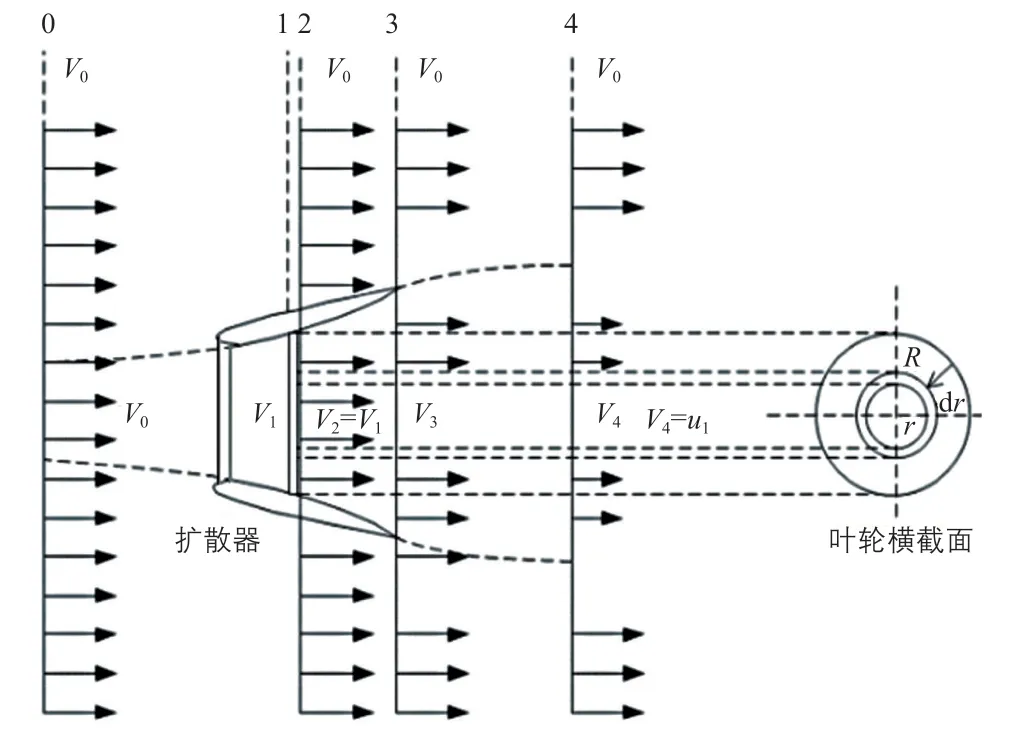
圖2 擴散型風力機的氣動原理示意圖Fig. 2 Schematic diagram of aerodynamic principle of DAWT

從圖2 可以了解：由于擴散器通流截面發生變化，下游的壓降導致風的質量流量增加，使到達葉輪的風速增大，從而提高了風電機組的輸出功率。

文獻[7]給出了擴散型風力機經典的風能利用系數Cp定義，即：

式中：ε為葉輪平面處風速與來流風速的加速比；β為葉輪掃掠面積與擴散器出口的橫截面積的面積比；ηd為擴散器效率。

其中，葉輪平面處風速與來流風速加速比可表示為：

葉輪掃掠面積與擴散器出口的橫截面積的面積比可表示為：

式中：A為葉輪掃掠面積，m2；A3為擴散器出口的橫截面積，m2。

擴散器效率的定義為：

式中：p2為葉輪平面(即圖2 中位置2)的靜態壓力，N/m2；p3為擴散器出口(即圖2 中位置3)的靜態壓力，N/m2；ρ為空氣密度，kg/m3。

根據擴散器出口處的能量守恒關系可得：

式中：cp3為擴散器出口的壓力系數。

其中，擴散器出口的壓力系數的定義為：

式中：p0為來流靜態壓力，N/m2。

將式(5)代入式(1)可得：

擴散型風力機上葉素的受力分析如圖3 所示。圖中：FN為法向分力，N/m；FT為切向分力，N/m；D為擴散器進口直徑，m；L為擴散器長度，m；θ為葉素扭轉角，(°)；φ為來流角，(°)；α為攻角，(°)；w為來流角風速，rad/s；W為軸向流速與來流風速的相對速度，m/s；Ω為葉輪旋轉角速度，rad/s；γ為擴散器內軸向流速與來流風速的比值；a、a′分別為考慮擴散器效應前、后的軸向感應因子。

圖3 擴散型風力機上葉素的受力分析Fig. 3 Force analysis of blade elements on DAWT

葉素的法向力系數CN和切向力系數CT的定義分別為：

式中：CL和CD分別為翼型的升力系數和阻力系數；c為葉素弦長，m。

葉素受到的推力dT、葉片對轉軸的轉矩dM和轉矩系數CM分別表示為：

葉片dr微元段上產生的功率dP可表示為：

由式(8)和式(10)可以得到：

式中：B為風力機葉輪的葉片數。

由式(9)和式(11)可以得到：

由以上各式可以得到：

式中：χ為尖速比。

尖速比的定義為：

最大尖速比λ和比例因子μ的定義分別為：

綜合以上公式，則式(1)的風能利用系數可表示為：

式中：P為風電機組的輸出功率，W。

從上述分析過程可見，式(20)所示的風能利用系數表達式，揭示了葉輪葉片、擴散器及風電場參數之間的關系。

2 優化設計案例

2.1 案例描述

以某企業額定功率為1 kW 的擴散型風力機作為研究對象，在確定的擴散器結構條件下，以擴散型風力機的風能利用系數最大為目標，將葉輪葉片橫截面上的葉素參數作為設計變量，對該風力機的葉片進行改進設計。

原風力機的相關參數為：葉輪葉片數為3；葉片翼型為NACA63-018；葉片長度為1.4 m；擴散器的擴散角為25°、長度為4.5 m、入口直徑為3 m；最大尖速比為4；當地空氣密度為1.225 kg/m3；取額定風速Vr為5.0 m/s，風力機額定轉速n=220 r/min。

2.2 設計流程及結果

將原風力機長度為1.4 m 的葉片分為14個截面，每個截面之間的間距為0.1 m。根據文獻[10]中建立的葉片優化設計模型，利用MATLAB 平臺編制程序，對沿葉展方向14 個截面葉素半徑處的葉素弦長c(r)和葉素扭轉角θ(r)等葉片結構參數進行優化計算，具體結果如表1所示。

表1 優化后的葉片結構參數取值Table 1 Values of optimized parameter for blade structure

2.3 葉素弦長和葉素扭轉角的擬合修正

表1 計算得到的優化參數中，葉片14 個截面的葉素弦長和葉素扭轉角呈現出非線性分布，且部分位置存在跳躍，加工制造的難度大，需要對其進行適當的修正。

本文采用基于最小二乘法的三次多項式擬合算法對優化參數進行修正，葉素弦長的數據點的坐標為(r/R，c)，葉素扭轉角的數據點的坐標為(r/R，θ)，則有：

式 中：a0、a1、a2、a3、b0、b1、b2、b3分 別為三次多項式中各階次的擬合系數。

在MATLAB 中編程，編制程序計算得到葉素弦長、葉素扭轉角的三次多項式擬合系數，分別代入式(21)、式(22)，則可得到葉素弦長的三次多項式擬合函數為：

葉素扭轉角的三次多項式擬合函數為：

2.4 優化設計結果

將擬合得到的14 個截面的葉素翼型坐標數據曲線分別導入到CAD 建模軟件SoildWorks 中，形成各葉素翼型的三維空間圖，如圖4 所示。

圖4 各葉素翼型的三維空間位置Fig. 4 3D spatial position of each blade element airfoil

然后通過軟件的“放樣”功能，將各葉素翼型閉合曲線形成實體的優化設計后的葉片模型，如圖5 所示。最后構建輪轂，并與葉片完成裝配，生成優化設計后的擴散型風力機的葉輪模型，如圖6 所示。

圖5 優化設計后的葉片模型Fig. 5 Blade model after optimized design

圖6 優化設計后的擴散型風力機的葉輪模型Fig. 6 Impeller model of DAWT after optimized design

2.5 數值仿真分析與對比

為探究本文對擴散型風力機葉片優化設計的效果，對葉片優化設計前、后的擴散型風力機進行仿真計算。應用Gambit 軟件對風力機及外部流場進行網格劃分，在Fluent 軟件中選用RNG( 重整規劃群)k-ε模型進行數值仿真。擴散型風力機的整體網格模型如圖7所示。

圖7 擴散型風力機的整體網格模型Fig. 7 Overall grid model of DAWT

在額定工況下，來流風速為5 m/s、風力機額定轉速為220 r/min 的條件下，優化設計前、后葉片的速度分布云圖如圖8 所示。

圖8 優化設計前、后擴散型風力機葉片的速度分布云圖Fig. 8 Cloud diagram of velocity distribution of DAWT blades before and after optimized design

從圖8 可以看出：在相同的風況條件下，擴散型風力機優化設計前、后的葉尖速度由68.3 m/s 提高到了102.0 m/s。

在風力作用下，葉片迎風面的受力為正壓，則迎風面為壓力面；背風面受力基本上為負壓，則背風面為吸力面；兩面存在的壓差使葉片產生升力，驅動葉片旋轉。葉片的壓力場是指在來流風作用于葉片時的壓力分布，葉片迎風面和背風面之間的壓差越大，能量損失越少，即獲能效率越高。相同風況條件下，優化設計前、后擴散型風力機葉片迎風面上的壓力分布云圖如圖9 所示。

圖9 優化設計前、后擴散型風力機葉片迎風面上的壓力分布云圖Fig. 9 Cloud diagram of pressure distribution on the windward surface of DAWT blades before and after optimized design

從圖9 可以看出：在相同的風況條件下，優化設計后葉片迎風面的壓力增高，這說明擴散型風力機運行過程中所受的阻力減少，降低了能量損耗，提高了風力機的獲能效率。

經計算，在額定工況下，該擴散型風力機實例機型優化設計前、后的葉輪轉矩由91.1 Nm 提高到130.1 Nm，風能利用系數由0.348提高到0.436。

3 結論

本文建立了一種用于低風速場景的擴散型風力機模型，尋求更適用于擴散型風力機獲能特點的葉片設計方法。針對某型號擴散型風力機，利用該模型開展了葉片結構參數的優化設計，并對優化設計前、后的風力機流場進行了仿真模擬分析。分析結果表明：在額定工況下，優化設計前、后擴散型風力機的葉尖速度、葉輪轉矩、風能利用系數等都得到了一定程度的提升。以期該研究結果可為小尺寸低風速風電機組的葉片設計提供可行方向。

需要說明的是，該模型在考慮風力機葉片幾何形狀的基礎上開展針對葉片結構的優化設計，計算成本較低。但該模型是將風力機葉片幾何結構簡化為一維線性流場進行描述，具有一定的局限性，只能用于擴散器、葉片的設計方案優化，詳細的流場特性計算仍需要借助CFD數值模擬。本文方法具有一定的潛在工程實用價值，鑒于篇幅所限未展示更多仿真結果，希望后續可通過樣機實驗對本文方法進行進一步的驗證和完善。