數學核心素養視閾下的初中幾何“一題多解”教學探究

金木紅

近年來，“核心素養”一詞在數學教育研究中“獨占鰲頭”，成為研究熱點。《義務教育數學課程標準（2022年版）》指出，數學課程要培養學生的核心素養，教會學生能用數學的眼光觀察世界，能用數學的思維思考世界，能用數學的語言表達世界。對一線教師而言，就是要將日常的教學經驗提取出來，以總結歸納出有效的核心素養的落地途徑。

教學的根本目的是“授之以漁”，不僅要教給學生必要的基礎知識，更要教給學生基本的學習方法，培養和發展學生的思維能力。初中數學教學過程中，在教育學生掌握和理解基礎數學知識的同時，還要培養學生用發散性思維多角度思考問題的能力。“一題多解”訓練就是啟發和引導學生從不同的角度，運用不同的思路和方法以及不同的運算過程，去分析、解答同一道數學題的練習活動。一題多解是諸多解題策略的綜合運用。這一教學過程中，學生的思維積極性得到充分調動，有利于開闊學生分析問題的視野和思路，有效鍛煉思維的靈活性，培養和發展學生對新舊知識的遷移能力，不斷促成學生初中數學核心素養的養成。在教學過程中，應積極適宜地開展“一題多解”的訓練，鼓勵學生運用“一題多解”力求找到最合理、最簡便的解法，將數學核心素養培養有機融入。下面筆者以幾個典型題目為例，通過開展“一題多解”教學，探究如何培養學生的數學思維能力和數學核心素養。

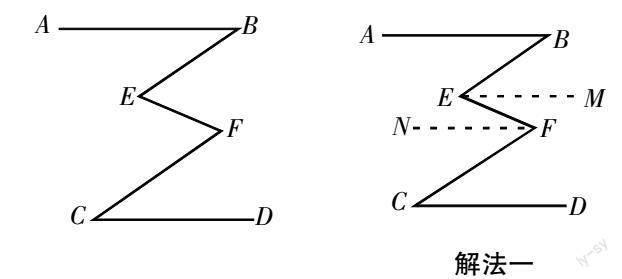
例1：如圖，已知∠A=∠F，∠DBA+∠DEC=180°.

請問，BD∥CE嗎？為什么？

解法一：因為∠A=∠F

所以DF∥AC

所以∠D=∠DBA

又因為∠DBA+∠DEC=180°

所以∠D+∠DEC=180°

所以BD∥CE.

解法二：因為∠A=∠F

所以DF∥AC

所以∠DEC+∠ECA=180°.

又因為∠DBA+∠DEC=180°.

所以∠ECA=∠DBA.

所以BD∥CE.

分析：本題是湘教版七年級數學下冊（義務教育教科書）平行線判定第2課時例題的一個變形題目，目的在于鞏固新知，檢測學生對平行線判定掌握的情況。并且本題可以應用一題多解，鼓勵學生開動腦筋，積極思考，培養學生的數學思維。本題難度不大，但由于七年級學生剛開始接觸幾何知識，所以能用兩種方法嚴謹地寫出解答過程還是有一定的挑戰的。課堂上，教師要留給學生充分的時間思考，并且鼓勵學生大膽嘗試用不同的解法來解同一道題目，要想數學思維得到提升，必須長期堅持“一題多解，一題多練”。

本題考查平行線判定，目前學習了三種方法來判定兩直線平行。解法一是利用構造同旁內角互補，判定兩直線平行。解法二是利用構造同位角相等，判定兩直線平行。

例2：如圖，已知∠B=∠C，AB∥CD.

解法一

試判定BE與CF的位置關系，并說明理由.

解法一：BE∥CF，理由如下：

過點E作EM∥AB，過點F作FN∥CD，

所以∠B=∠BEM，∠C=∠CFN

又因為∠B=∠C

所以∠BEM=∠CFN

又因為AB∥EM，AB∥CD，FN∥CD，

所以EM∥NF

所以∠MEF=∠EFN

則∠BEM+∠MEF=∠CFN+∠EFN

即∠BEF=∠CFE

因此BE∥CF.

分析：本題仍然是考查平行線判定，但是較例1而言，難度上升了許多。題目要求證明BE∥CF，但是BE與CF之間并沒有同位角、內錯角、同旁內角，所以本題需要添加輔助線，這是本題需要最先突破的一個點。學生認真觀察圖形后能意識到這一點，但是怎樣構造輔助線成了解決此題的“攔路虎”。善于思考的學生會類比例1來構造同位角、內錯角或者同旁內角。解法一是大多數學生容易想到的，過拐點作平行線，構造內錯角相等，從而得到兩直線平行。但是此方法要用到多次平行，書寫過程也比較麻煩，初學者邏輯語言不夠熟練，也容易出錯。考試時建議用簡單、準確、快捷的方法來提高解題效率。因此，教師可以引導學生尋求更簡便的方法來解答，鼓勵學生積極思考，充分發揮學生的邏輯思維能力和分析能力，從而取得突破。本題對于剛剛開始接觸幾何學習的七年級學生來說確實有一定的難度，但是只要老師耐心引導，分解難度，給學生充分的思考空間，相信一定會有學生找出更優的解題方法。

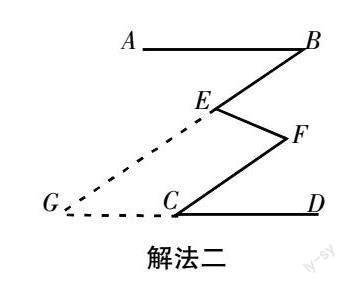
解法二：BE∥CF，理由如下：

延長BE，DC交于點G.

因為AB∥CD

所以∠B=∠G

又因為∠B=∠FCD

所以∠G=∠FCD

因此BE∥CF.

解法三：BE∥CF，理由如下：

連接BC.

因為AB∥CD

所以∠ABC=∠BCD

又因為∠ABE=∠FCD

∠EBC=∠ABC-∠ABE

∠FCB=∠BCD-∠FCD

所以∠EBC=∠FCB

因此BE∥CF.

分析：顯然解法二和解法三比解法一要簡單得多，巧妙地避開了二次平行的煩瑣轉化。學生想到這些方法，說明對平行線的性質和判定已經熟練掌握，學習達到一種更高層次。解法二是延長BE，DC交于點G.構造∠G=∠FCD，利用同位角相等，從而兩直線平行。解法三是連接BC，利用AB∥CD，找到內錯角∠ABC=∠DCB，再運用等量減等量差相等，得到∠EBC=∠FCB，利用內錯角相等，兩直線平行。兩種方法都是構造角的關系，但是后面兩種解法一步到位，直接找到同位角、內錯角是由BE與CF兩條被截線產生的，簡單明了，考試肯定首選這兩種解法。當然本題也還有其他解法。

解法四：BE∥CF，理由如下：

過點F作FN∥CD，延長BE交FN于點G.

因為FN∥CD

所以∠NFC=∠C

又因為AB∥CD，FN∥CD

所以AB∥FN

所以∠B=∠EGF

又因為∠B=∠C

所以∠EGF=∠NFC

因此BE∥CF.

[A][B][C][D][E][F][G][N]

解法四

解法五：BE∥CF，理由如下：

過點E作直線MN交AB與點M，交CD于點N，交FC于點G.

因為AB∥CD

所以∠BME=∠GNC

又因為∠B=∠C

所以∠MEB=180°-∠B-∠BME

∠CGN=180°-∠C-∠GNC

所以∠MEB=∠CGN

又因為∠CGN=∠EGF

所以∠MEB=∠EGF

因此BE∥CF.

[A][B][C][D][E][F][G][M][N]

解法五

分析：解法四是過點F作FN∥CD，并延長BE交FN于點G.構造內錯角∠EGF=∠NFC，從而得到BE∥CF;解法五是過點E作直線MN交AB與點M，交CD于點N，交FC于點G。構造同位角∠MEB=∠EGF，從而得到BE∥CF。兩種方法殊途同歸，都是通過添加輔助線，構造內錯角或者同位角的關系來判定兩直線平行。

需要注意的是，學生剛接觸初中幾何，教師一定要循循善誘做好適當的引導，不能完全放手。特別是基礎比較薄弱的學生，他們容易犯難，如果多次做不出來，容易灰心喪氣，甚至放棄學幾何。當學生能比較熟練解答幾何題目后，教師也要學會適當放手，給予學生足夠的時間思考，并要求他們寫下解答思路，并分享給大家。還要鼓勵學生大膽嘗試其他的做法。長期堅持每道幾何題目都爭取用兩種以上的方法來證明，這樣學生解答幾何題目的數學思維一定能培養起來，也能很好地培養數學核心素養。

以上幾道例題是筆者在平時課堂教學中，所任教班級的學生主動展示的解題方法。學生們大膽地發言，嚴謹地敘述解答過程，甚至課后主動把題目和解答過程認真整理書寫在錯題本上，作為教師，筆者倍感欣慰。教學應該是以學生的動機和發展需要來展開的。教學不是一味地按照課本進行，而是教師與學生共同探討，一起決定學習的內容和建構知識的過程，是挖掘、拓展教材深刻內涵的過程，是開發和創新課程的過程。只有這樣的教學才能使教師和學生得到共同的成長。

“一題多解”運用在教學中并不是單純地尋找多種解法，它有兩個作用：一是從多個角度分析有助于挖掘問題的深層結構;二是利用一個問題來聯系不同的知識點，幫助學生形成知識結構體系。在一題多解中要注意從以下幾個方面培養學生的創造思維能力和數學核心素養。一要注意培養學生的發散性思維;二要注意啟發學生的靈感;三要充分利用“學生渴求他們未知的、力所能及的問題”的心理，培養學生創新的興趣（例如：田忌賽馬、將軍飲馬、勾股定理等）;四要積極鼓勵學生發現問題、提出問題、討論問題、解決問題，通過質疑、解疑，讓學生具備創新思維、創新個性、創新能力。

弗里德曼《怎樣學會解數學題》中強調：“解題不僅僅是為了找到答案”，他說：“應當學會這樣一種對待題目的態度，即：把習題看作是精密研究的對象，而把解答題目看作是設計和發明的目標。”可見，一題多解訓練，有利于學生更好地理解數學的概念、定理及其知識體系，養成從整體的角度思考問題和解決問題的習慣，形成舉一反三、追根溯源的能力和敢于探索、勇于創造的精神，從而更好地把握數學學科的知識結構和本質特征，最終達到潛移默化地培養學生數學核心素養的目的。

總之，數學教學應該建立在學生興趣的基礎上。因此，數學教學應體現學生的主體參與，教師要有效引導學生發現問題、提出問題、探索并解決問題，讓他們在“學中做，做中學”的過程中不斷成長。在數學課堂教學中，教師應根據知識點、考點、難點、易錯點精選典型題目，鼓勵學生積極探索多種解法，從而激發學生內心深處的創新意識。同時，在此過程中，教師需要引導學生站在系統的高度用聯系的觀點看待教材各部分知識，幫助學生不斷總結與反思解決問題的方法和技巧，進一步加強學生認知的開發，使學生真正領悟數學思想和方法，逐步提升數學思維，培養數學核心素養。

參考文獻：

吳正憲.數堂教學策略：師生互動共同創建有效課堂[M].北京：北京師范大學出版社，2010.

（作者單位：銅仁一中初級中學）

編輯：曾彥慧