在初中數學解題中有效應用數形結合

李明超

數形結合是一種常見的解題方式，它的應用不僅可以打開學生的思維，還能提升學生的解題效率。本文以初中數學為研究對象，簡述了數形結合思想，分析了采用數形結合思想開展教學的優勢，并以案例的方式對其在解題中的應用進行深入的研究。

新課程理念指導下的數學教學不單注重學生知識學習，更加強培養學生的數學思維。針對這一現實情況，教師必須改變陳舊的教學模式，在開展基礎教學的同時，加強對學生數學思維的培養，讓學生在主動參與中獲取知識、提升能力。教師應用數形結合這一教學方法，可以幫助學生建立起系統思維模型，提升學習效率。因此加強數形結合思想在數學解題中應用的研究非常重要。

一、數形結合思想概述

數形結合即數與形的對應，教學中教師通過數與形間的轉化可以讓學生輕松地解答問題。隨著教學改革的發展，教師的教學理念也在發生轉變，從知識教學轉向學習思想的培育。數形結合模式在解題中的應用，降低了學生的數學學習難度，深化了學生對知識的理解。教師將數形結合思想應用于數學解題中，不僅解決了解題的難點，而且提升了學生的解題效率。教學改革的持續發展，使各個階段的教育獲得了發展，在為國家培養創新人才方面發揮著重要的作用。但人才的培養是一個長期的過程，特別是要打好基礎。數學作為初中階段的一門基礎學科，因抽象性、邏輯性強的特點加大了學生的學習難度。數學教學不僅要注重學生的知識掌握度，更要關注學生數學思維能力的發展，由此數形結合的思想就進入了大家的視野，并在課堂教學中得到了廣泛的應用。

二、初中數學教學中應用數形結合法的優勢

（一）應用范圍廣，適用于不同類型的數學知識

以往的初中數學教學形式單一，教師往往采取“灌輸”的方式，力圖通過詳細地向學生分析數學知識來達到讓學生理解的目的。在這一過程中，學生機械地學習，讓數學學習失去原本的魅力。長此下去，學生在數學課上就會消極，采用單一的學習方法，固化了數學思維。而數形結合是數學思想方法的一種，主要通過數和形的相互轉換來解決實際問題，因此這一方法得到了廣泛應用，而且根據不同的知識點可以展現出不同的效果，以此優化數學課堂。

（二）涉及思想方法，拓寬學生的數學思維

數形結合是數學思想的一種，它強調靈活解讀和應用，是數學知識內化的一種表現。加強數形結合思想在初中數學中的應用，可以幫助學生把握知識的內在關聯，通過長期的訓練可以促進學生數學思維的發展。將數形結合思想應用于不同問題的解答中，可以讓學生認識到思想方法的重要性，通過汲取數學思想和方法完善自己的學習體系。

（三）鍛煉解題技巧，提升學生的解題效率

數形結合不單是解決問題的有效方法，更是一種思維的體現。學生通過數形結合思想的學習可以解決數學難點，可以達到舉一反三的效果，用它來解決更多的問題，也可以促使學生形成一種思維模式，在長期的堅持和鍛煉中掌握解題技巧，這對學生日后的成長與發展有著現實意義。

三、初中數學教學現狀

剛進入初中的學生，因其思維、學習方法還停留在小學階段，所以在學習中會出現各種問題。升入初中后學習的難度會逐漸加大，這不僅影響著學生的學習效果，而且會導致學生降低學習興趣，從而讓學生無法全身心地進入數學課堂中。教師在教學中應用數形結合思想，幫助學生更輕松地掌握知識，提高課堂質量。但受到傳統教學形式的影響，當下的課堂教學中還存在諸多問題。

（一）教師教學方法單一

在以往的數學課堂中，教師會采取“灌輸”的模式開展，并試圖通過“題海”戰術讓學生掌握某個知識點，這不僅加大了學生的壓力，而且限制了學生的發展。針對這一現實情況，教師只有加強創新和優化教學方法，才能為數學課堂注入更多的趣味元素，才能在這種思想方法的引導下習得知識、解決問題，并促使學生更好地學習。

（二）數學難度大，降低了學生的學習熱情

從小學到初中，數學學習的難度明顯加大，這就導致部分學生在課堂的收獲甚微，從而打擊了學生的信心，降低了學習熱情。教師應用數形結合思想則可以輕松地解決這一問題，通過數和形的轉變可引發學生深入思考，以此來降低學習難度，讓學生有效理解知識，為其數學綜合思維能力的發展打下堅實的基礎。

（三）教師忽視數形結合思想

數形結合思想在學生數學學習中發揮著重要的作用，特別是在初中階段，貫穿著整個過程，對其的應用影響著學生解答問題的速度與能力。但在以往的教學中很多教師都忽視了對其的應用，忽視了在解題中滲透數形結合思想，認為教學的重點在于解決實際問題。其實不然，應用數形結合思想是學生必備的一項能力，特別是初中生正處在形象思維向抽象思維過渡的階段，加強數形結合思想的學習非常重要。

四、數形結合在初中數學解題中的有效應用分析

在數學問題的解決中學生只有靈活應用知識，并通過有效的訓練才能獲得更多的答題技巧，也才能進一步提升自身解決實際問題的能力。而在這一問題的解決過程中，加強數形結合思想方法的應用可以將題目中的條件直觀地展現出來，便于學生理解其中的含義，并最終提升學生解決問題的能力。

（一）巧用數形結合思想解決正數和負數問題

剛進入七年級的學生，思維還處在形象階段，面對難度更大、抽象性更強的數學知識點，只有在教師的引導下才能完成，才能進一步提升其數學思維能力。例如，在正數和負數的概念的教學中，教師便可以采用數軸的方法對學生進行引導，首先在黑板上畫出一個數軸，中點表示為0，左邊為負數，右邊為正數，然后再創設“氣溫低于0度和氣溫高于0度”的生活情境，讓學生將-5度、-10度和+5度、+10度刻畫在數軸上，以幫助學生把握正數和負數的概念。這一簡單應用，給了學生啟發，而且在接下來的重點學習中，學生也可以舉一反三，結合這一思想方法解答問題。

（二）巧用數形結合思想解決函數問題

函數是中學階段的學習重點，但由于函數的抽象性和邏輯性，學生在函數學習中出現了各種問題。所以在學習中，教師可以指導學生采取數形結合的方法對一元一次方程、一元二次方程以及二元一次方程進行歸納，將其特點展現出來，方便學生理解和接受，進而在解答方程問題時能夠游刃有余。為了深化學生的學習，教師可以設置問題“一次函數與二次函數存在哪些異同點”，此時學生就會想到利用數形結合思想進行解答，首先在紙上畫出一次函數y=kx+b和二次函數y=ax2+bx+c（且a≠0）的圖象，學生便可以清晰看到兩者的區別。然后再根據對不同函數圖象的分析，讓學生認識到了一次函數和二次函數各元素的作用，為學生后續根據各元素的作用解答問題提供了特定的條件。

（三）巧用數形結合思想解答幾何問題

初中數學幾何知識的范圍很廣，有三角形、平行四邊形、圓形和圓柱體知識等，為了幫助學生探究其中的本質，教師可以應用數形結合思想。比如，在“勾股定理”這節知識的教學中，教師可以為學生展示生活類的問題，讓學生根據所學的知識和以往的經驗進行解答，然后利用數形結合思想將題目中的條件轉化為直角三角形，再利用勾股定理知識解答現實問題。

例如，“老師要求同學們測量學校旗桿的高度，小明發現旗桿頂端的繩子垂到地面后還多出1 m，當他把繩子的下端拉開5 m后，發現繩子下端剛好接觸地面，你能幫助小明求出旗桿的高度嗎？”根據題目的條件，學生可以畫出相應的圖形，而后會發現旗桿和地面兩者的結合正好是直角三角形的兩條直角邊，然后會聯想到所學的勾股定理知識，再根據勾股定理的概念和公式，自然可以列出勾股定理的方程。求解：設繩子的長度AB為x m，則旗桿的高度AC為（x-1） m，在直角三角形ABC中，得出AC2+BC2=AB2，也就是（x-1）2+52=x2，由此可以得到x=13，則x-1=12，所以旗桿的高度為12 m。

又如，在圓的有關知識的學習中，為了提升學生對圓的認識，教師可以指導學生利用數形結合的思想，分析圓和圓的位置關系，而后加深學生的印象。最后教師再設計相應的習題，鼓勵學生解答，不但豐富了學生的知識儲備，而且提升了學生解答數學問題的效率。

（四）巧用數形結合思想解決數學不等式問題

學生若采取傳統的方法解答不等式，需要求出每一個不等式的解集，在數軸上畫出來，然后找到不等式的公共部分便可以得到不等式組的解集。因此，在這部分知識點的教學中，教師可以從簡單的題目入手，在學生熟悉數形結合思想方法后，再加大學習難度，為學生多設計幾個題目，最后邀請學生將自己解題的方法和過程展現出來。有的學生采取了直接計算的方法，有的學生用數軸表示，這是學生數學思維和數學能力的充分體現。為了開闊學生的思維，教師可以將班內學生劃分為不同的小組，指導學生以小組的方式求出如下的二元一次方程組：x+2y=2m-5x-2y=3-4m，若x為正數，y為負數，求m的取值范圍。本道題目和以往的二元一次方程求解不同，因為題目中有未知數m，但教師可以指導學生結合數形結合的方法進行思考。在小組討論中，深得數形結合思想方法的學生會提出采取數軸的方法解答，然后根據題目中給出的條件，得到m的取值范圍。經過長期的訓練，學生不僅掌握了不等式的解答方法，而且為日后利用這一數學思想方法解答更高難度的問題奠定了基礎。

（五）巧用數形結合思想解決線性規劃問題

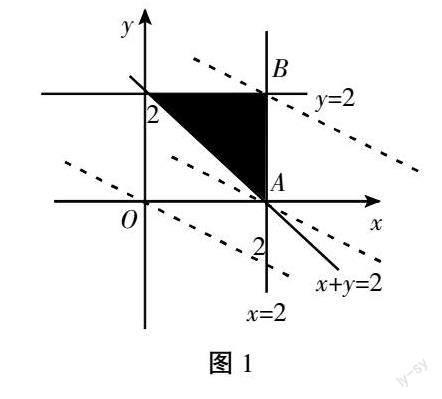
數形結合方法是解決線性規劃問題的有效方法，在此類問題的解答中，根據題目給出的條件作圖，然后通過分析找出正確的區域，最后進行作答。例如，在解決如下線性規劃問題“若x、y、z滿足約束條件x≤2，y≤2，x+y≥2，則z=x+2y的取值范圍是多少？”時，就可以引導學生采用畫圖的方式畫出x與y的數軸（如圖1），然后根據題目中給出的條件進行繪制，再通過觀察與分析就可以輕松得到問題的答案。

由上可見，在線性規劃問題的解答中，利用數形結合法解答問題非常重要，但需要學生畫出正確的區域，才能根據題目條件得到正確的答案。因此在此類問題的解答中，學生必須牢記數形結合方法，如此才能提升學生答題的速度和準確率。

綜上所述，初中生只有靈活應用知識，在問題的解答中才能更加游刃有余。同樣，教師引導學生利用數形結合思想解決問題，可以使復雜問題簡單化，可以將抽象的數學語言以直觀的圖形展示出來，可以幫助學生把握住數學問題的本質。而且大量的教學實踐研究顯示：數形結合思想的應用，可以促進學生的全面提升與發展，在當下的數學教學中發揮著重要的作用。數形結合是一種先進的數學思想，教師對其的應用創新了教學模式，因此在日后的教育教學中，教師要將數形結合的思想融入數學問題的解答中，通過創新模式、細化目標，吸引學生主動參與，同時激活學生的數學思維，將學生的內在潛力挖掘到位，為學生數學核心素養的形成奠定堅實的基礎。

參考文獻：

[1]金明.映“數”“形”花別樣紅：數形結合思想在初中數學解題中的應用[J].新課程（中學版），2014（1）：218-219.

[2]馬威.數形結合思想在初中數學解題中的應用[J].中學生數理化（教與學），2021（35）：71-73.

[3]胡麗琴.數形結合思想在中學數學解題中的應用[J].中華少年（研究青少年教育），2012（7）：315-316.

[4]王靜.淺析數形結合思想在初中數學解題中的應用[J].世紀之星（初中版），2022（11）：172-174.

（作者單位：貴州省興仁市波陽鎮田灣中學）

編輯：張俐麗