數字信號處理技術在電路虛擬仿真實驗中的應用

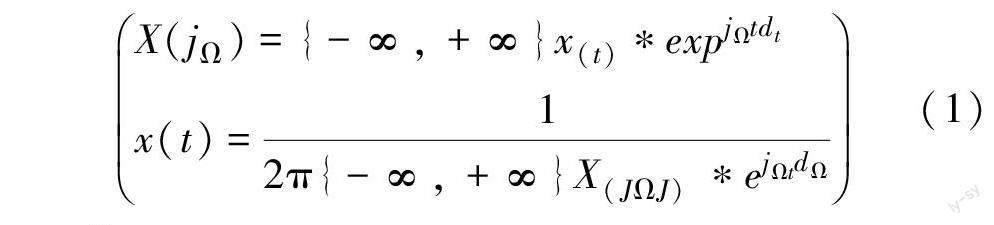
關鍵詞：數字信號；處理；仿真；應用

中圖法分類號：TN911 文獻標識碼：A

數字信號處理是智能化設備的重要基礎，在利用智能化技術對外部信號進行處理的過程中，首先需要將外部傳感器信號轉變為電路可傳輸的數字信號，才能夠通過單片機或中心處理器進行計算與邏輯安排。基于此，數字信號是智能化設備的應用核心，也是電路仿真實驗中的重要一環。當前，針對數字信號處理的方式主要采用基爾霍夫定律來進行實現，本文也將在簡述其原理的基礎上對此技術在仿真中的實際應用及應用效果進行分析。

1數字信號處理的基本原理

在電路中，數據的表征方式一般是二維的，即通過通電“1”和斷電“0”來進行表征。這一特征與電路數字信號傳輸的穩定性相關，在此前的研究中也有利用電壓等方式對復雜信號進行模擬的嘗試，但穩定性無法達到當前芯片對數據處理的要求而擱淺。因此，在數字信號處理的過程中，將傳感器收集到的外部數據利用電路中的“0和1”進行表征是信號數字化的基本原理。

數字信號處理大體上可以分為3個基本步驟。其一是利用電路將外部獲取的模擬信號轉變為穩定的數字信號；其二是對數字信號進行加工與分析；其三是按照運算結果將輸出的數字信號再次轉變為模擬信號（如圖1所示）。數字信號的處理重點需要解決由模擬信號向數字信號的轉變。外部傳感器所獲得的信號是一種模擬信號，如一種聲音、溫度變化等。在電路中需要通過必要的電路系統將模擬信號轉變為數字信號。模擬信號在通過傳感器后是以電信號的形式所存在的，如當傳感器接收到一段聲音后，聲音震動的頻率與幅度會改變電路中電流的大小。

此時，模擬信號已經轉變為一段以電流為載體的數字信號，但是未經過加工的數字信號會存在一定的失真與雜音，其產生的方式與原理較為復雜。同樣以聲音為例，不同波動對于電流大小的改變并非完全線性的，而在特定頻率下會產生“跳遷”，進而影響轉化的效率與準確性。這就需要采用必要的手段對獲得的初始信號進行進一步的加工，具體包括過濾、降噪等，在運算時則需要采用篩選、變換、濾波、放大等方式使其形成穩定、可靠，且可供后續數字信號處理器識別的有效數字信號。其中.濾波技術是一個極為關鍵的實現手段，根據電容對于電流波動性的消解作用，以電磁放大的具體手段將接收到的數字信號進行放大，并對其展現的恒流波進行電子整合，以形成與模擬信號呈現出良好線性關系的數字信號，進而保障數字信號的還原度與真實性。

2數字信號處理算法及仿真技術

數字信號的處理方式除了硬件的支持，還需要對其具體算法進行實現，進而保障實驗過程的穩定性及可靠性。同時，為了快速地對相關技術進行認證，在實物實驗前開展仿真計算，以達到更高的便捷性。

2.1數字信號處理算法

目前，針對數字信號處理所采用的主要方法是離散型傅里葉變換（DFT）。此方式的核心是在接收到仿真信號后在數據域和頻域的雙維度上進行特定參數的離散（見式1）。

通過式1中不難發現，傅里葉轉換過程中的Xj的電阻系數是表征系統內電路電信號的關鍵，并與電阻最大化的奇數成正比例關系，而以時間作為周期轉換周期與所形成的頻域信息及產生的周期呈負相關關系，而對于不符合周期性的電信號則予以去除。在實際應用中，DFT首先對數據域和頻率域進行離散，然后利用DSP等專用的數據處理設備對信息總體進行離散化。同時，可以采用FFT技術對離散系數進行求解，此方式大大減少了DFT的計算次數，實現了對數字信號的真正高效加工，從而促進了傅里葉技術的發展與拓寬實際應用的廣度。傅里葉轉換是數字信號處理過程的重要組成部分，它的時延性和運算性能是表示數字信號的關鍵。值得注意的是，由于傅里葉轉換應用的廣泛性，當前存在一種專門的單片機對傅里葉轉換模型進行計算，從而使得針對數字信號的處理更為便捷。無論是從頻域還是從數字信號的角度出發，都可以把時間域的信號轉化為頻域，也可以把頻域的信息轉化為時間域，因為所探測到的信息大部分具有一定的連續周期。也正是基于這一原理，如雜音、系統雜波等由于沒有連續的周期性，進而能夠在傅里葉轉換中得到有效的規避與消解，所轉換后的數字信號與原有模擬信號之間的線性相關性相對較好，在二次還原后能夠得到更為精準的模擬信號。

2.2數字信號處理的仿真技術

離散傅里葉轉化是一種數學方法，在具體的實現過程中可以通過電子處理的方式予以實現，同時可以利用電路結構予以實現。如何利用電路結構實現對數字信號的處理則是仿真工程中所需要解決的關鍵性問題。因此，在開展仿真實驗的過程中，開發者往往采用模塊化方式對具體的電路進行構建，通過對數字信號處理單元的建模來實現對相關信號的處置。

目前，仿真模擬技術已被廣泛應用到各個領域。這種技術可以利用計算機技術以及虛擬現實的方式創造出一種可以讓人感覺不到的虛擬環境，并對虛擬設定的電路進行運行，以觀察電路中不同結構的功能與狀態。這種基于模擬與仿真所建立的環境和空間雖然僅供參照，不能作為最終影響結果進行使用，但是對于技術的迭代以及前期觀察具有積極的意義。將虛擬模擬技術應用于實驗中，可以對實驗結果進行觀察分析，以最快的速度檢驗該系統的合理性。與此同時，通過對電路設計創意的實驗，可以從性能設計、邏輯設計、模擬測試等方面來體現其功能，使其能夠更好地向受試者展示電路運行的真實狀況。通過對電路工作和環境的仿真，可以實現對系統性能的直接影響，且對于調試等必要環節均能夠提升其效能。目前，常用的仿真程序包括Multisim和OrCAD等。除了上述優勢，利用仿真的方式進行電路設計還能夠極大地降低成本，并保障使用者的安全。

3數字信號處理算法在仿真實驗中的應用

為進一步認證本文所探討的數字信號處理算法的有效性，以基爾霍夫定律作為驗證的主要手段，以Multisim為仿真工具，對實體電路進行仿真搭建，并分析其主要指標效果，具體結果如下。

3.1實驗設計

本文以Multisim為仿真軟件對數字信號處理模塊進行仿真建設，并利用試運行的方式確定仿真技術下數字信號處理技術的具體應用方式。在此實驗中利用Multisim提供的元件庫對具體線路進行構建，包括電源系統、線路以及信號的接收模塊及其等效電阻。在仿真單元構建完畢后，實驗的開展具體包括如下幾個步驟：其一，對仿真線路進行搭建與建模，并規范各個節點之間的檢測依據；其二，在仿真環境下，利用直流電源認證不同電氣元件之間的可靠性，通過基爾霍夫定律求解不同電子元件的闡述設定，以及與輸入信號之間的線性關系，為后續的數字信號處理提供參數上的支持；其三，利用交流電源的輸出模擬數字信號處理的真實運行情況，分別對不同節點之間工作點的運行狀態進行掃描，從而獲得數字信號處理技術的總體濾波效率，并對輸出結果的穩定性以及準確性進行判斷。通過此實驗結果的對比，能夠充分了解在仿真條件下所設計的數字信號處理系統的真實運行狀態，為后續的實物搭建以及單片機產品設計提供參考與指導。

3.2仿真設計

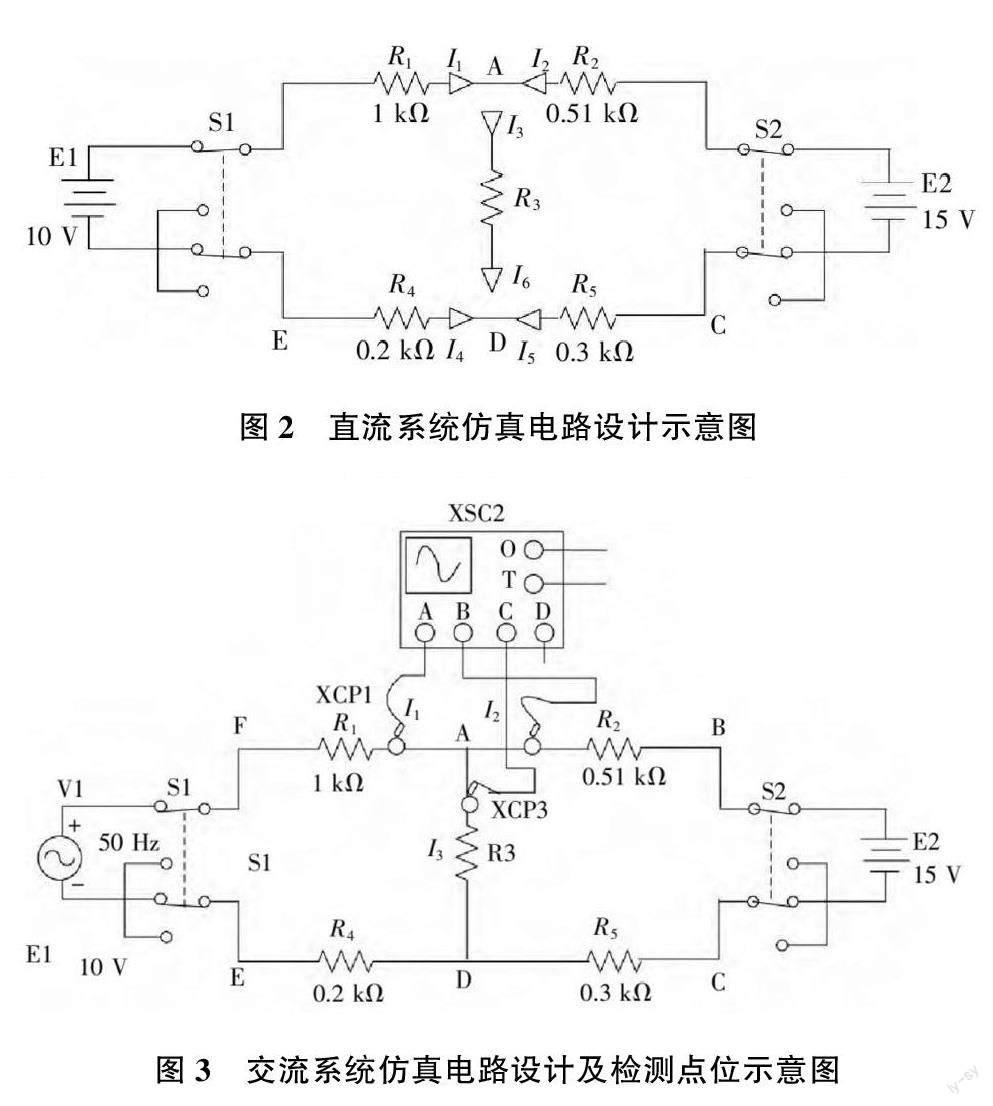
通過對仿真軟件Multisim構建對應的電路系統，來實現對數字信號的處置，如圖2所示。其中，El為輸入電源，用來仿真外部傳感器的電信號輸入（將模擬信號轉變為電信號在傳感器內部可以完成），其后通過轉換電路實現對雜波的物理過濾，并實現有效的放大。E2作為電路自身的電源供給對信號的放大提供能源支持，根據對不同點位的電流檢測可以獲得多維度的電信號信息，作為仿真結果的輸出端。仿真電路有2個開關組.S1和S2作為輸入與輸出信號的控制單元。與此同時，不同電路線路中設置等效電阻，以防止仿真過程中短路情況的出現。上述電路在直流通電情況下，并未出現短路等情況，線路運行狀態良好，支路電流的分配符合基爾霍夫定理的分配原則，證實了仿真電路系統真實有效。

在完成直流條件下的電路合規性檢驗后，對交流電路進行仿真設計。交流電路的基本模式及構成方式與直流類似，其中傳感器的電信號采用交流進行模擬。同時，布置示波器對電信號進行接收，并以示波器的0，T端作為數字信號的輸出端口。在示波器的布置上，A點接人通過Ri的電阻電流，B點接入通過R2的電阻電流，C點接入通過R₃，的電阻電流。利用示波器的波形整合及放大對數字信號進行輸出，并對輸出結果的質量進行判斷。具體如圖3所示。

3.3實驗結果

在上述仿真電路中，實際聯通交流電源后（E1）不同點位掃描電流結果如表1所列。

由表1可以發現，當中心電阻R₁阻值發生變化時，總體電路的電信號處理效率存在明顯的變化，且呈現出明顯的先升高后下降的趨勢，但總體的電信號處理質量均超過90%。這說明，此仿真模式下數字信號處理系統能夠有效滿足電信號的處置需求，并提供穩定的輸出信號。但是，電路自身對于輸出效能的影響也較為明顯，影響的方式為電路自身的等效電阻呈現出“倒U型”趨勢，在二次函數模擬的情況下可以發現其峰值出現在805～1050Ω。因此，在實際設計中采取線路等效電阻在950Ω左右，其處于最佳的處理區間。在該區間中，本次數字信號處理技術的仿真結果顯示出最大的處理準確性。

而從I₁的指標來看，該指標作為示波器的輸入單元，代表了初始數字信號的進入強度，在數字信號的放大過程中，信號質量會存在一定的弱化，因此輸入電流越高越好。從表1的結果中不難發現，隨著等效電阻的逐步增加，輸入電流呈現出明顯的降低趨勢，當等效電阻從205Ω，提高到1050Ω時，輸入電流從0.009718下降至0.004 301，下降幅度為48.66%，這一指標也進一步說明在進行數字信號處理的過程中等效電阻的阻值不能超過1000Ω。當然，若提高輸入電壓（傳感器數字信號電壓），則會在一定程度上規避此現象造成的影響，但需要傳感器系統消耗更多的能源，也客觀上提高了傳感器系統的造價。

作者簡介：

王軍章（1977—），大專，助理工程師，研究方向：電子信息工程。