基于余弦-指數非線性混沌映射的射頻隱身抗分選信號設計技術

賈金偉,韓壯志,劉利民,解輝

(陸軍工程大學石家莊校區 電子與光學工程系,河北 石家莊 050003)

0 引言

現代雷達面臨干擾、反輻射攻擊等嚴重電子對抗威脅[1]。雷達射頻隱身技術能夠降低雷達信號及其參數被電子偵察系統截獲和識別的概率,提高雷達電子防御能力[2-3]。通常,雷達告警接收機等寬帶實時電子偵察設備的偵測過程可分為信號截獲、分選和識別3個階段。與之對應,雷達射頻隱身[4]主要有抗截獲[5-7]、抗分選[8]和抗識別3類手段。其中,抗分選就是使電子偵察系統無法從隨機交錯的脈沖流中分離出各個雷達脈沖序列,是對抗電子偵察系統的一個重要突破點[9]。從兩個方面對信號分選技術進行梳理：

1)一方面,從對信號的分選處理流程來分析。信號分選主要分為預分選和主分選兩個過程。預分選是通過脈沖的載波頻率(Radio Frequency,RF)、脈沖寬度(Pulse Width,PW)、到達方向(Direction of Arrival,DOA)對脈沖進行分類,實現對高密度脈沖流的稀釋。主分選是輻射源信號分選的核心,通常是通過對各個脈沖的到達時間(Time of Arrival,TOA)進行處理,進而得到電磁環境中各個輻射源的脈沖重復間隔(Pulse Repetition Interval,PRI)及其調制方式[10]。所以,要削弱電子偵察系統對信號的分選,首先要對抗基于TOA的主分選。

2)另一個方面,從對信號分選的研究方向來分析。雷達輻射源信號分選技術主要有3個研究方向：基于脈間調制特征的雷達輻射源分選、基于脈內調制特征的雷達輻射源分選和基于機器學習的雷達輻射源分選[11]。基于脈間調制特征的雷達輻射源分選主要是基于脈沖TOA對信號PRI進行分選。基于脈內調制特征的雷達輻射源分選主要是通過提取更穩定、更細微、參數交疊更少、區分度更高的脈內調制特征來解決信號分選問題。基于機器學習的雷達輻射源分選是利用機器學習在數據分析、分類及預測等領域的特長對信號進行分選。雖然在每一個研究方向都有一大批研究成果,但應用于雷達告警接收機等寬帶實時電子偵察設備時均存在不同程度的不足。基于脈內調制特征的雷達輻射源分選需要提取脈內更加細致的特征,所以此類方法計算量普遍較大,且抗噪性表現較差,難以適應電磁環境的復雜變化。基于機器學習的雷達輻射源分選的不足是需要預先獲取大量非合作輻射源信號樣本進行訓練集,在實際應用中有較大難度。同時機器學習中的信號分選模型需要經過較長時間的訓練才能收斂,難以滿足戰場實時性要求。因此,寬帶實時電子偵察設備仍以基于脈間調制特征的雷達輻射源分選方法為主,結合與業內信號分選工程實踐領域專家討論交流的成果,序列差值直方圖(Sequential Difference Histogram,SDIF)算法及其改進算法是信號分選工程實踐領域廣泛使用的核心算法。所以,抗分選主要是對抗基于TOA的SDIF分選算法。

當前,抗分選研究主要聚焦于抗分選信號設計技術。主要包括干擾脈沖抗分選[12-15]、抖動PRI抗分選[14,16-17]和PRI優化抗分選[18-19]等方式。上述方法雖然取得了一定的效果,但信號在設計時沒有以分選失效原理作為基礎,制約了信號的設計效率。

本文研究PRI分選算法中經典SDIF算法的失效原理,并以此為基礎,運用一種改進的一維混沌系統,設計射頻隱身抗分選信號,并通過仿真驗證信號的抗分選性能。。

1 抗分選信號設計原理

抗分選信號設計原理主要是通過對信號分選算法的研究,分析得出分選失效機理,進而為抗分選信號的設計提供理論支撐,提高信號抗分選設計的效率和成功率。

1.1 基于SDIF的分選算法

雷達信號源分選,又稱雷達輻射源信號去交錯,是指從隨機交錯的脈沖流中分離出各個雷達脈沖列的過程,本質是上是信號各個脈沖的參數匹配問題。在實際的工程領域內,最常用的是直方圖分選方法。直方圖分選方法是借鑒統計學原理對輻射源信號的PRI值進行估計。通過統計TOA的差值,形成TOA差值直方圖,然后設置合適的分選門限和分選策略。工程上常用的改進算法主要有累計差值直方圖(Cumulative Difference Histogram,CDIF)算法和SDIF算法兩種。

從本質上講,SDIF和CDIF算法都屬于TOA差值直方圖分選算法。兩種分選算法都是按照一定的規則對脈沖的TOA差值進行統計,分析得出PRI估計值,然后根據PRI估計值進行脈沖序列搜索,將輻射源脈沖序列提取出來[20-21]。與傳統的直方圖分選算法相比,SDIF和CDIF算法大幅度降低了計算量,滿足實時性的要求,可以對PRI固定、PRI參差和抖動的輻射源信號進行分選,在工程領域中得到了廣泛應用[22-24]。

與CDIF算法相比,SDIF算法具有以下優點：一方面SDIF算法不累積不同級別的直方圖統計值,只統計分析當前級別的直方圖,同時取消了2倍PRI檢測,減少了計算量、提高了處理速度;另一方面,SDIF算法對門限函數進行了優化改進,與子諧波檢測相配合,避免了虛假檢測的發生。因此,SDIF算法的應用更為廣泛。SDIF信號分選算法流程如圖1所示。

圖1 SDIF信號分選算法Fig.1 SDIF signal sorting algorithm

由圖1可知,SDIF分選算法主要包括對TOA差值直方圖的分析和脈沖序列搜索兩部分。TOA差值直方圖分析主要是用來估計PRI值。運用直方圖統計的方法將從1階開始對逐級TOA差值次數進行統計。如果TOA差值統計次數存在超出檢測門限的峰值,那么峰值對應的TOA差值除以TOA差值統計級數就是可能存在的PRI值。SDIF算法的門限函數為

Tthre(τ)=a(E-C)e-τ/kN

(1)

式中：τ表示PRI值;a是可調常數,一般由脈沖丟失率確定;E是脈沖總數;k是[0,1]內的常數;N是直方圖統計的小區間個數。

在SDIF分選算法對信號的實際分選過程中,為避免截獲接收機對脈沖TOA測量誤差的影響,同時增強算法對抖動信號的分選性能,所以在SDIF及其改進的分選算法中,設置了信號PRI值T的容差ε,即PRI小盒。小盒的上、下限分別為

Tmax=T+ε

(2)

Tmin=T-ε

(3)

(4)

式中：xi為容差內單個Ti對應的脈沖數量;S為容差內鄰近PRI值T1,T2,…,Tn對應的脈沖數量總和。

1.2 分選失效原理

1.2.1 1階直方圖的分選失效原理分析

1.2.1.1 信號PRI值由1個增加為有限多個

根據式(1),PRI的值τ=τ0時,算法的門限值為

Tthre(τ0)=a(E0-1)e-τ0/kN

(5)

PRI的值τ=τ1時,算法的門限值為

Tthre(τ1)=a(E0-1)e-τ1/kN

(6)

(7)

由于E0表示脈沖總數,通常有成千上萬個,E0?1。所以,式(7)簡化為

(8)

所以,對式(8)取自然對數后,可得τ′為

τ′=kNln (2a)

(9)

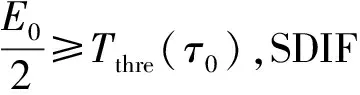
τ′=kNln (na)

(10)

因此,當信號的PRI值增為有限個,SDIF算法無法分選出PRI小于臨界值kNln(na)的信號脈沖。

1.2.1.2 信號PRI值服從區間分布

假設脈沖數量仍有E0,PRI值為區間分布,即τ∈[τmin,τmax]。因為在雷達領域需要統籌考慮發射信號的設計與回波信號的處理兩個方面,所以雷達信號PRI值不會是完全的隨機無序分布,通常采用多個PRI值貫序重復發射的方式。因此,在本節內以信號PRI值服從均勻分布進行討論。對于區間內任一確定的τ,其脈沖數量E′為

(11)

式中：τmax和τmin為分布區間的最大值和最小值;z為區間分布內PRI值的最小間隔。PRI的值為τ′時,算法的門限計算公式如式(1)所示。

當Tthre(τ′)=E′時,

(12)

所以,式(12)簡化為

(13)

因此,求解出分選失效的PRI臨界值τ′為

(14)

綜上所述,在1階直方圖的分選失效原理分析中,若信號PRI值服從區間分布,在區間長度大于區間間隔的20倍時,區間內PRI值對應的脈沖數量均小于分選算法的門限值,SDIF算法分選失效。

1.2.2 多階直方圖的分選失效原理

SDIF分選算法在1階直方圖中存在多個過門限的PRI值時,需要統計2階、3階至高階直方圖,進而得出PRI估計值,所以同樣需要對2階至高階直方圖的分選失效原理進行分析。

門限函數如式(1),在2階至多階直方圖中,只是直方圖階數C發生變化,與脈沖總數E相比,E?C,所以門限公式近似無變化。因此,信號PRI值服從區間分布的時候,1.2.1節中1階直方圖對于SDIF算法分選失效原理的分析仍然適用。

通過第1.2節的分析討論,當雷達信號PRI值服從長度為PRI最小間隔20倍以上的區間分布時,信號脈沖在各階TOA差值直方圖的累積量均小于分選算法門限,將導致分選算法失效。

1.3 關于抗分選信號設計原理的討論

信號分選是指從隨機交錯的脈沖流中分離出各個輻射源脈沖列的過程,其本質是利用脈沖流中各脈沖之間的相關性,將屬于同一個輻射源的脈沖序列相互匹配,進而實現信號分選。

根據第1.2節的分析,在雷達信號PRI值服從長度為PRI最小間隔20倍以上的區間分布時,降低了脈沖流中同一輻射源各脈沖之間的相關性,使得同一輻射源的各脈沖之間呈現弱相關性,進而導致信號脈沖在各階TOA差值直方圖的累積量均小于分選算法門限。

因此,為進一步減少脈沖序列之間的相關性,強化其隨機性,基于前文失效機理,利用強隨機性的混沌序列對信號PRI進行調制,提高雷達信號抗分選性能。

2 基于CE混沌映射的信號設計

2.1 混沌模型

混沌系統是一種存在確定表達式的非線性系統,表達式經過多次迭代,系統會表現出很強的隨機性、初值敏感性和不可預測性。由系統產生的混沌信號在時域和頻域分布上類似于噪聲,具有較寬的頻帶和長期的不可預測性,主要分為一維混沌系統、二維混沌系統和高維混沌系統[25-30]。與隨機系統不同的是,由于混沌映射表達式是確定的,所以混沌系統也是確定的。因此,混沌系統產生的混沌信號既具有類似于噪聲的隨機性又具有混沌的確定性。類似于噪聲的隨機性增強了信號的抗分選性能,所以在符合第1節抗分選信號設計原理的基礎上,運用混沌系統對信號的PRI進行調制,信號的抗分選性能亦有所提升。

考慮到系統對序列生成的要求和工程實踐中對混沌系統復雜度、運算量的限制,一維混沌系統由于其高效、快捷被廣泛使用。典型的一維混沌映射有Logistic映射、Chebyshev映射、Cubic映射,各映射對應的表達式分別如式(15)～式(17)所示：

xn+1=rxn(1-xn),xn∈[0,1]

(15)

xn+1=cos (parccos (xn)),xn∈[-1,1]

(16)

(17)

式中：r為Logistic映射的控制系數,r∈[0,4],當r≥3.57時,系統處于混沌狀態[31];p為Chebyshev映射的控制系數,當p≥2時,系統處于混沌狀態[32];q為 Cubic映射的控制系數,當q≥2.3時,系統處于混沌狀態[33]。3種映射處于混沌狀態時,均表現出比較低的混沌狀態,不利于抗分選信號的設計。為此,受到典型的Logistic映射啟發,本文設計一種基于余弦-指數的一維非線性混沌映射,混沌映射主體是三角函數余弦函數,余弦函數內部包含πrxnexn(1+x)和π(exn+x3)兩部分,第1部分πrxnexn(1+x)是產生混沌序列的主體,第2部分π(exn+x3)主要是通過指數項和高次項進一步增強第1部分所產生混沌序列的隨機性和不可預測性,如式(18)所示：

(18)

引入cos函數的目的是為了將混沌映射的輸出值控制在[-1,1]之間,這樣可以將信號的PRI中心值與混沌映射的輸出中心值0相對應,映射輸出值1和-1可以對應任意的PRI變化范圍極限。第2部分的指數項πexn消除了初始值不能為0的限制,使得混沌序列的產生更加靈活,且系統是否進入混沌狀態不再受控制系數值的限制,能夠更快地進入混沌狀態,如圖2所示。

圖2 本文所提出的混沌映射分岔圖和序列點圖Fig.2 The chaotic mapping bifurcation diagram and sequence point diagram proposed in this paper

2.2 基于CE混沌映射的調制信號

根據第1節抗分選信號設計原理,當雷達信號PRI值服從長度為PRI最小間隔20倍以上的區間分布時,信號脈沖在各階TOA差值直方圖的累積量均小于分選算法門限,將導致分選算法失效。因此,信號設計原理為設計信號指明了PRI捷變需服從的區間長度,運用強隨機性的混沌序列對信號PRI進行調制時,PRI捷變的區間長度至少大于區間最小間隔的20倍。

信號的PRI值T根據CE混沌映射產生的序列進行調制,調制函數如式(19)所示：

Tn=T0+xn·ΔT

(19)

式中：T0是信號PRI中心值;ΔT是信號PRI最大變化量。調制后的PRI值序列仍具有混沌序列的隨機性,但如圖3紅色圈所示,混沌映射調制的PRI值序列存在多值窄間隔效應,即序列中存在多個相鄰的脈沖PRI值之間間隔較小,導致相鄰的脈沖落入同一個脈沖分選容限內。

圖3 PRI調制后的多值窄間隔效應圖Fig.3 Plot of multi-valued narrow interval effect after PRI modulation

因此,在混沌序列對PRI值進行調制之前,需要對混沌序列的生成方法進行改進,以消除多值窄間隔效應。在混沌映射每生成一個序列值xn,首先要對xn及上一個值xn-1進行間隔判斷,若間隔滿足要求,則保留該值xn,將xn代入混沌映射表達式進行下一步的迭代產生xn+1,再判斷xn+1與xn之間的間隔,依次類推;若間隔不滿足要求,則舍棄xn,判斷xn-1與由xn迭代產生的xn+1之間的間隔是否滿足要求,若滿足間隔要求,保留xn+1,若不滿足間隔要求,則舍棄xn+1,比較xn-1與xn+2,直至得到滿足要求的混沌序列值。同時,為了濾除部分集中在序列值邊界的點,對滿足間隔要求的序列點值增加了臨界值判斷步驟xn+Δx<1和xn-Δx>-1。具體的信號PRI序列生成流程如圖4所示。

圖4 PRI序列生成流程圖Fig.4 Flow chart of PRI sequence generation

3 仿真驗證

3.1 混沌序列的性能仿真

3.1.1 混沌映射性能分析

為了進一步說明本文所提出的CE混沌映射的優點,選用典型的一維混沌映射Logistic映射、Chebyshev映射、Cubic映射與本文所提映射對比,從混沌映射的分岔圖、最大李雅普諾夫指數(LE)、近似熵、平衡性方面進行分析比較：

1)混沌映射的分岔現象是映射進入混沌狀態的標志之一,通過描繪映射的分岔圖可以直觀地觀察到映射的混沌區域和映射中的控制參數對混沌的影響。下面根據Logistic映射、Chebyshev映射、Cubic映射和本文所提映射4種映射的表達式繪制分岔圖,如圖5所示。

圖5 4種混沌映射分岔圖Fig.5 Bifurcation diagrams of four chaotic mappings

由圖5所示：Logistic映射只有在分形系數r≥3.57時,系統才會進入混沌狀態,當0≤r<3.57時,系統處于周期狀態;Cubic映射在分形系數r≥2.3時,系統進入混沌狀態,當0≤r<2.3時,系統處于周期狀態;Chebyshev映射在分形系數r≥1.5時,系統進入混沌狀態,當0≤r<1.5時,系統處于周期狀態;本文所提出的CE混沌映射不受分形系數的影響,分岔圖中的各點在圖中分布更加均勻。

2)最大 LE是用來評估混沌序列的隨機性,其定義如式(20)所示：

(20)

式中：f′(xi)表示混沌映射f(xi)=xn+1的1階導數。當最大李雅普諾夫指數大于0時,表示系統處于混沌狀態,其值越大表示系統產生的混沌序列隨機性越強。下面繪制上述4種具有不同分形系數的混沌映射LE變化曲線,如圖6所示。

圖6 不同混沌映射的LE對比Fig.6 Lyapunov index comparison diagram of different chaotic mappings

由圖6可知,Logistic、Chebyshev以及Cubic 3種映射LE并不是一直大于0,表明了3種系統并不是一直處于混沌狀態。以Logistic映射為例,只有當r≥3.57時,系統才處于混沌狀態。本文所提出的混沌映射在分形系數變化區間[0,4]中,其LE除了個別點小于0,其他均大于0,避免了分形系數的限制。同時,LE大于另外3種一維混沌映射,表明本文所提的CE混沌映射生成的混沌序列比另外3種一維混沌映射生成的混沌序列具有更強的隨機性。

3)近似熵主要是衡量由混沌映射生成混沌序列的復雜性。近似熵值越大代表序列具有更高的復雜性。在相同的仿真條件下計算上述4種映射的近似熵,其中分形系數取值從0.5到4.0以步長為0.5變化,序列長度設置為10 000。得到的結果如表2所示。由表中的計算結果可知,當系統沒有進入混沌狀態時,近似熵的值極小甚至為0。例如,當r=0.5和r=1.0時,Logistic、Chebyshev以及Cubic 3種映射的近似熵值在10-5或10-7數量級,Chebyshev映射在r=1.0時,近似熵值為0。而本文所提的混沌映射在分形系數變化區間內,均保持大于1的近似熵值,表明該映射產生的序列具有更高的復雜性。

表2 4種不同混沌映射的近似熵值隨分形系數的變化Table 2 The approximate entropy of four different chaotic mappings varies with fractal coefficients

4)載波的壓縮性能與序列的平衡性密切相關。如果混沌映射生成的序列是非平衡的,會導致載波泄露,造成信息丟失和干擾。平衡性與序列長度有關,通常認為其值小于0.01即滿足要求。平衡性計算公式如式(21)所示：

(21)

通過對式(15)～式(18)的分析以及結合對混沌映射的運用背景,本文序列的區間設置在[-1,1]內,所以,式(21)中X為序列中0的個數,Y為序列中1和-1的個數。序列長度值設置為[500,10 000],其他的仿真參數不變,得到平衡性結果如圖7所示。

圖7 不同混沌映射的平衡性對比圖Fig.7 Contrast diagram of balance of different chaotic mappings

由圖7可知,Cubic映射生成的序列平衡性數值隨著序列長度的變化遠大于臨界值0.01,會導致信息泄露,信號的載波壓縮性能較差。Chebyshev映射生成的序列平衡性能與本文提出的混沌映射所生成的序列相對接近,但是Chebyshev映射生成的序列在個別長度仍會出現平衡性數值超過0.01的情況。本文提出的混沌序列與Logistic混沌序列平衡性數值均小于0.01,表明二者序列的平衡性更好。

3.1.2 PRI序列性能分析

如圖8(a)和圖8(b)所示,通過本文提出的混沌映射對信號PRI直接進行調制時存在多值窄間隔效應,這不利于PRI值的跳變,極易導致相鄰的PRI值落入相同的PRI容差范圍內,所以提出了混沌映射寬間隔調制PRI的方法。仿真具體參數如下：PRI中心值為2 ms,PRI變化范圍為1 000 μs,分選算法的PRI容差為200 μs,即相鄰的兩個信號脈沖之間的PRI至少相差100 μs,混沌序列先迭代 1 000次,從1 001次開始調制,以排除混沌系統的初值影響。為便于仿真分析,混沌序列長度設置為50。仿真結果如圖9所示。

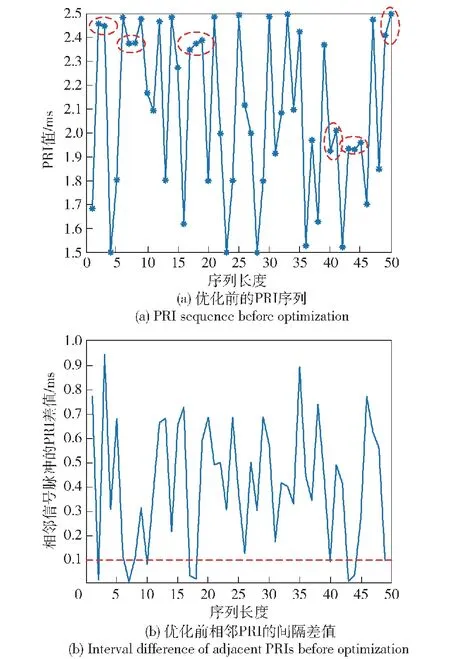
圖8 優化前的PRI序列及相鄰PRI的間隔變化Fig.8 PRI sequence before optimization and the interval change diagram of adjacent PRIs

圖9 優化后的PRI序列及相鄰PRI的間隔變化Fig.9 The optimized PRI sequence and the interval variation diagram of adjacent PRIs

由圖9可知,本文所提出的方法優化了PRI序列的生成方法,消除了多值窄間隔效應,很好地滿足了PRI差值間隔要求,增強了信號的抗分選性能。經過對圖8和圖9的仿真結果的分析,可以看到本文設計信號的靈活性。一方面,運用混沌序列對信號的PRI進行調制可以充分利用混沌系統的初值敏感性、分形系數敏感性,為信號PRI值提供了更廣泛的變化范圍。另一方面,對于信號PRI在不同工作條件下的設計具有更大的靈活性。PRI序列可以根據設計的信號總長度一次生成,也可以截成幾段多次生成,這樣得到的PRI序列同樣是不同的。

3.2 信號設計原理仿真驗證

信號設計原理指出當所設計的雷達信號PRI值服從長度為PRI最小間隔20倍以上的區間分布時,信號分選失效。因此,在設計信號時,PRI區間長度至少應大于20倍最小間隔。為驗證信號設計原理對于設計信號的正確性和重要意義,本節進行對比仿真。仿真參數設置如下：信號共計1 000個脈沖,TOA測量誤差為50 ns。信號的PRI中心值為 1 250 μs,PRI區間最小間隔為2 μs,PRI捷變的區間長度分別為最小間隔的20倍和15倍,即PRI區間為[1 230 μs,1 270 μs]和[1 235 μs,1 265 μs]。1階直方圖分析范圍為0～2 500 μs,直方圖統計間隔為0.5 μs。SDIF算法統計門限如式(1)所示,式中N=5000、k=0.1、a=0.8。SDIF算法分選結果如圖10所示。

由圖10(a)所示,當信號PRI的區間長度大于等于20倍的區間最小間隔時,區間內任意的PRI值對應的脈沖統計數量均小于SDIF的門限值,SDIF算法分選失效。同時,圖10(a)亦可說明本文設計的信號在PRI抖動幅度只有20 μs,抖動量只有1.6%的小抖動幅度下仍具有抗分選能力。由圖10(b)所示,當信號PRI的區間長度小于20倍的區間最小間隔時,區間內個別的信號脈沖統計數量超過門限值,能夠被信號分選算法成功分選。本次仿真驗證了信號設計原理的正確性,證明了設計原理為抗分選信號設計提供有力的理論支撐。

3.3 信號的抗分選性能仿真

仿真參數設置如下：信號共計1 000個脈沖,TOA測量誤差為50 ns。信號的PRI中心值為2 ms,PRI變化范圍為1 000 μs,1階直方圖分析范圍為 0～2 500 μs,直方圖統計間隔為0.5 μs。SDIF統計門限如式(1)所示,式中N=5 000、k=0.1、a=0.8。SDIF分選結果如圖11所示。

圖11 1階～4階TOA差值直方圖Fig.11 First-order to fourth-order TOA difference histograms

由圖11(a)所示,在1階SDIF直方圖分選算法中根本沒有超過門限的信號,所以可以實現抗分選。圖11(b)～圖11(d)表明,在2階、3階、4階SDIF直方圖分選算法中雖然有超過門限的信號脈沖,但累計數量均沒有超過5個,所以信號脈沖不會進入分選流程。綜合分析圖11(a)～圖11(d),經過本文所提出的混沌映射調制的信號可以實現抗分選的效果。

3.4 與PRI隨機抖動信號抗分選對比仿真

在信號抗分選領域,PRI隨機抖動信號也被認為是抗分選性能較好的信號之一[16]。本節以PRI隨機抖動信號為例,與本文設計的信號就抗分選能力進行對比。抖動信號的PRI中心值為2 ms,抖動量為1 ms,即抖動信號的PRI區間為[1 500 μs,2 500 μs]。PRI隨機抖動信號是PRI在[1 500 μs,2 500 μs]區間內服從隨機分布。本文設計的信號是PRI在[1 500 μs,2 500 μs]區間內由混沌序列調制產生。本次待分選信號共有1 000個脈沖,仿真結果如圖12所示。

圖12 抗分選性能對比仿真圖Fig.12 Comparison simulation diagram of anti-sorting performance

如圖12所示,圖12(a)中PRI隨機抖動信號直方圖在紅色圈所標記的地方超過分選算法的檢測門限,信號極易被SDIF算法分選,圖12(b)中雖然也存在信號TOA差值直方圖超過分選算法門限的情形,但對比二者可以發現,在本文分析的信號設計原理指導下,由混沌序列調制的信號在直方圖中僅有極少的信號直方圖超過門限,而PRI隨機抖動信號的直方圖出現很多超過門限的情形,表明本文設計的信號在抗分選性能方面優于PRI隨機抖動信號。

4 結論

為了加強雷達的射頻隱身能力,本文對抗分選信號的設計原理及設計方法進行分析研究。得出以下主要結論：

1)詳細研究SDIF分選算法,提出基于SDIF門限函數的抗分選信號設計原理。原理指出：當雷達信號PRI值服從長度為PRI最小間隔20倍以上的區間分布時,信號脈沖在各階TOA差值直方圖的累積量均小于分選算法門限。

2)設計了一種新型映射,該映射生成的序列在復雜性和隨機性方面均顯著優于經典一維混沌映射所生成的序列。

3)在抗分選信號設計原理的基礎上,結合本文的混沌映射設計了一種寬間隔PRI信號。仿真結果表明,該信號具有更大的靈活性,滿足了抗分選的要求,提高了信號的抗分選性能,為抗分選信號的設計提供了一種重要途徑。