噴嘴長度對射流式施肥器性能影響的數值研究*
俞曉峰,姚麗萍,2,陳濤,謝守勇,2,李光林,2
(1.西南大學工程技術學院,重慶市,400715;2.丘陵山區農業裝備重慶市重點實驗室,重慶市,400715)
0 引言
水肥一體化借助微灌技術,是一種節水節肥的精準化灌溉技術。其中,施肥裝置及其性能是影響灌溉施肥質量的關鍵,目前,國內外常用的施肥裝置有壓差式施肥罐[1-2]、注肥泵[3-4]、文丘里式施肥器[5-9]以及射流式施肥器等。其中,射流式施肥器屬于液液混合中心射流泵的小型化應用,主要利用從噴嘴噴出高速射流的卷吸作用在吸肥腔內部產生負壓,進而將肥液從母液桶中吸出并與主管道水流混合,最終進入滴灌系統中送至作物根系。相較于其它傳統施肥器,射流式吸肥性能好、工作范圍廣以及混合程度高;同時其在運行過程中振動與流量波動更小,從而使其在水肥混合調控中具有更高的穩定性。
射流式施肥器性能的主要影響因素包括吸肥腔結構參數、喉管長度、噴嘴結構以及空化特性等。相關學者現已開展了大量的研究工作。汪小珊等[10]對8種不同規格的射流式施肥器進行了性能測試,并推導了進出口壓差與進口壓力之間關系的公式,研究得到公式斜率主要受喉管截面和噴嘴出口截面的面積比的影響;袁寄望等[11]研究了吸肥腔收縮角、吸肥腔直徑以及喉部直徑比等結構參數對射流式施肥器吸肥性能的影響,并對這些結構參數進行組合優化設計;在液液混合中心射流泵的研究中,龍新平等[12]數值研究結果表明喉管長度與射流泵面積比有關,并確定了射流泵的最優喉管長度及其范圍;袁丹青等[13]設計了一種多噴嘴射流泵,可以通過縮短主管水流和被吸流體混合均勻長度來減小喉管長度。周良富等[14]利用理論與數值計算相結合的方法研究射流式混藥裝置結構參數對其性能影響,結果發現面積比以及噴嘴出口與混合式吸入口之間的距離對性能影響最大,并通過分析獲得參數最佳取值范圍。在射流泵空化特性研究方面,Liu等[15]在對大面積比的中心射流泵的數值模擬中觀察到空化氣泡均是從吸入腔與喉管相接處產生并向下游延伸,隨著時間演化呈現周期性波動;Xu等[16]通過實驗驗證了由速度梯度引起的壓力脈動可以作為預測空化的判據;Wang等[17]通過實驗研究了射流泵在不同喉管長度、喉管類型以及擴散角下的空化特性,結果表喉管結構對空化強度有顯著影響。當射流式施肥器進出口壓差增大到一定數值之后(正常工況外)會發生劇烈的空化現象,從而限制吸肥能力進一步提升[10]。現有的報道中關于射流式施肥器的研究集中于正常工況下吸肥腔結構對吸肥性能的影響。射流式施肥器中吸肥腔是水肥混合的核心部位,而其內部結構尤其是噴嘴長度(不同的噴嘴長度對應不同的噴嘴結構),是影響吸肥其性能的關鍵因素。然而,目前不同噴嘴長度射流式施肥器的空化特性對吸肥性能影響方面的研究鮮有報道,亟需進一步研究。
基于此,本文提出采用計算流體力學手段對不同噴嘴長度的射流式施肥器吸肥性能進行研究,并對其影響機制進行調查分析,以強化施肥器的吸肥性能。首先研究了施肥器在不同進出口壓差下吸肥量的變化規律;然后,調查了噴嘴長度對吸肥量、吸肥濃度、進口流量比和吸肥效率等性能指標的影響規律;最后,通過對施肥器內部流場分析,揭示了不同噴嘴長度空化特性對吸肥性能影響的機制。
1 問題描述和數值公式
1.1 物理模型
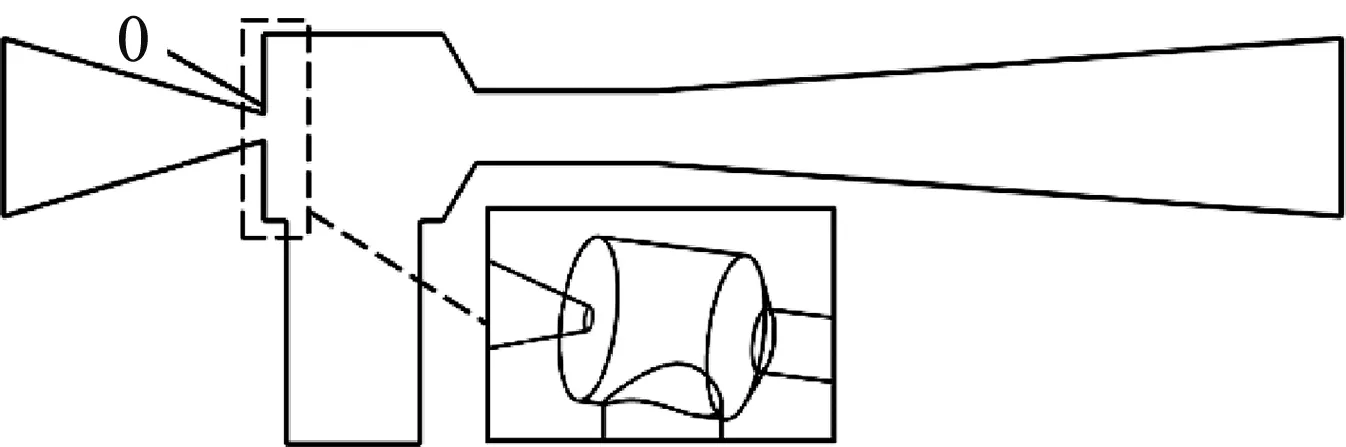
本文所采用射流式施肥器結構模型如圖1(a)所示,主要包括收縮段、吸肥腔、吸肥管、喉管、擴散段和出口五個部分組成。工作時,主管道水流由進口流入,經收縮段后流速變大形成高速射流,在吸肥腔經卷吸作用形成負壓,將肥液由吸肥口吸入管道,并與水在喉管中混合后由擴散段流出進入管路中。建立主管道的水流方向為x軸方向,肥料進入吸肥管道的方向為y軸方向,z軸方向符合右手螺旋定則。相應的截面示意圖如圖1(b)所示,射流式施肥器總長為150 mm,其他主要結構參數進口直徑D1、出口直徑D2、吸肥口直徑DT、收縮段角度α、擴散段角度β、噴嘴口直徑d1以及喉管直徑d2,主要結構尺寸見表1。

表1 射流式施肥器關鍵結構尺寸參數及特征表Tab.1 Key structural and dimensional parameters and characteristics of jet fertilizer injector
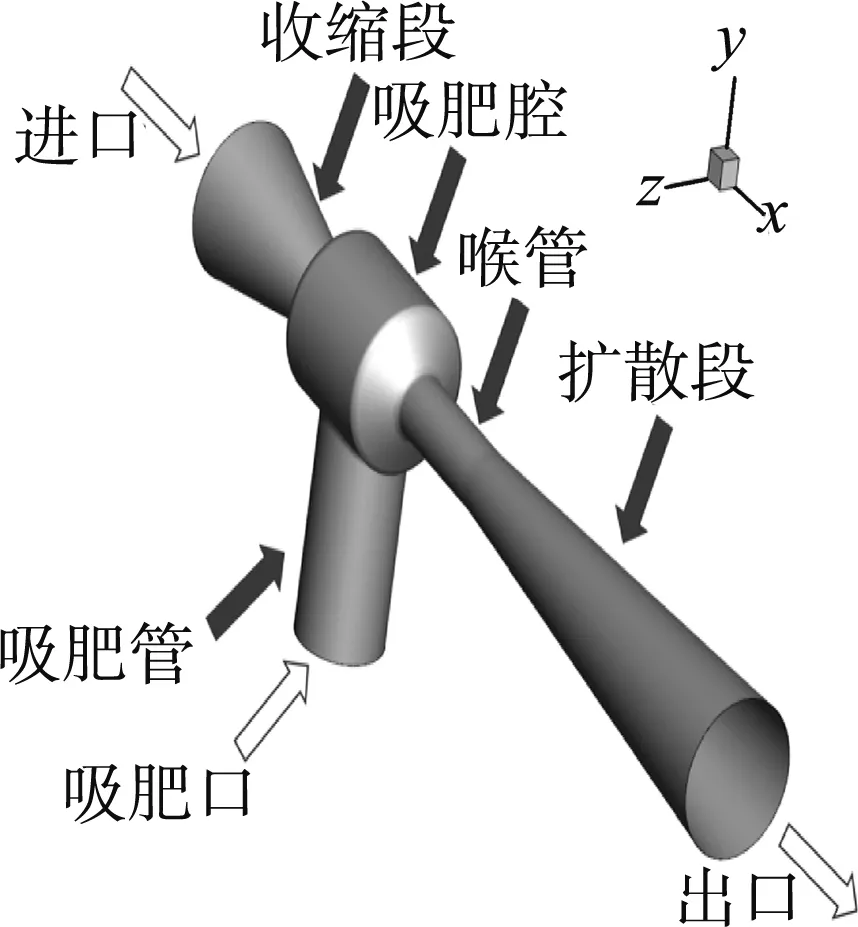
(a) 結構模型
在施肥器吸肥腔結構中,有一根正好貫穿吸肥腔并與吸肥腔圓柱長度L一致的管道[10],即為噴嘴,其長度始于與收縮段連接處,止于噴嘴出口。
1.2 基本控制方程
本文假設射流式吸肥器內部為不可壓縮流體,且不考慮溫度場的變化,湍流模型采用標準k-ε模型進行數值模擬,其中湍動能系數k及湍動能耗散率ε的運輸方程如式(1)~式(4)所示。
(1)
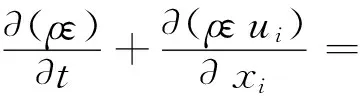
(ε/k)(Cε1P+ρCε2ε)
(2)
(3)
μt=Cμρ(k2/ε)
(4)
式中:ρ——流體密度;
μ——動力黏度系數;
ui——速度分量;
k——湍動能系數;
ε——湍動能耗散率;
t——時間;
μt——湍流黏度;
δk——湍動能k對應的普朗特數;
δε——湍動能耗散率ε所對應的普朗特數;
P——湍動能生成項。
經驗常數Cε1=1.44,Cε2=1.92,Cμ=0.09,δk=1.0,δε=1.3。
空化流動的數值模擬基于均相流模型,采用ZGB質量運輸空化模型,其中氣相質量運輸方程如式(5)所示。
(5)
式中:αn——氣相體積分數;


(6)
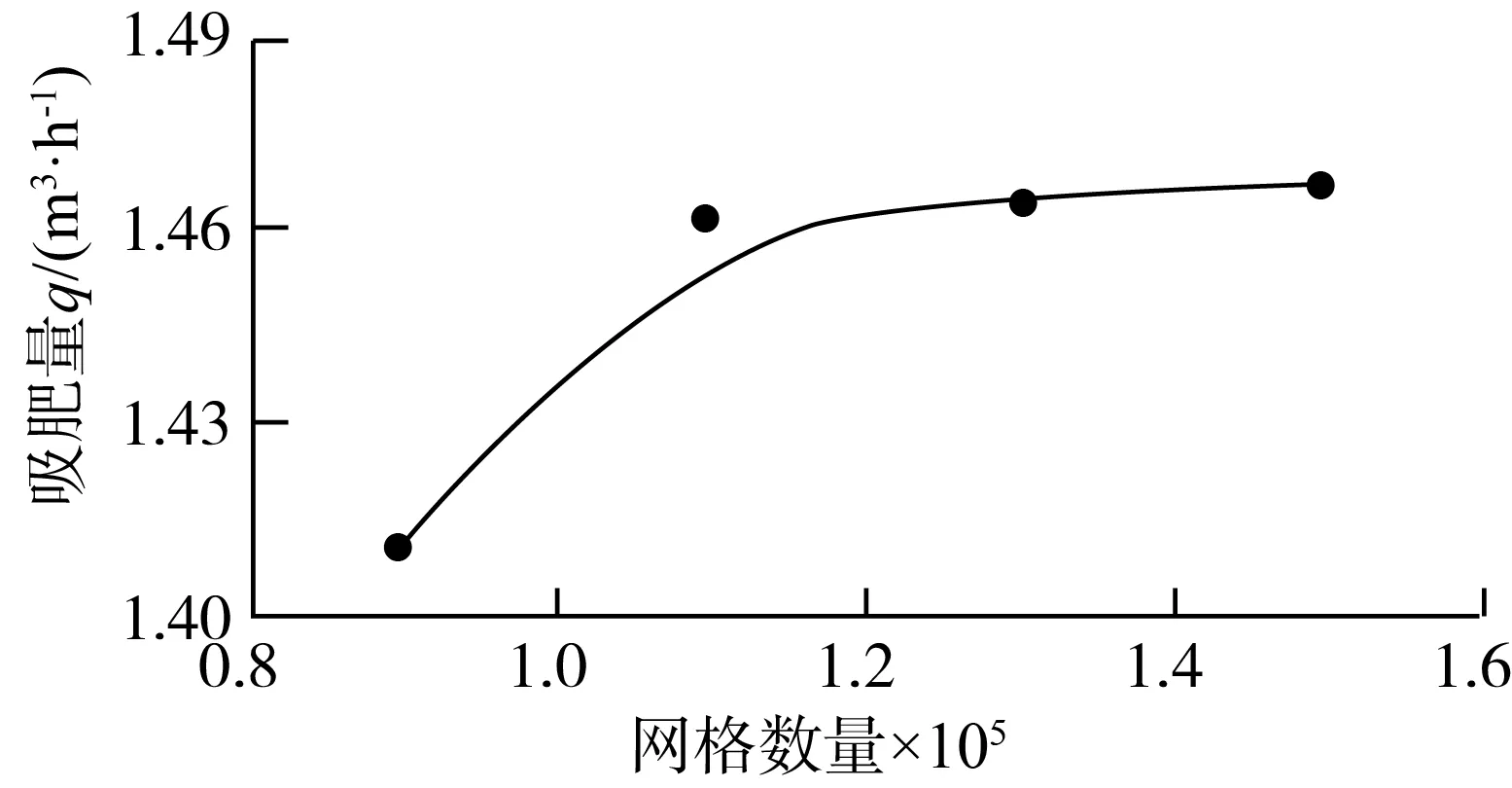
p (7) 式中:Fvap、Fcond——蒸發系數和凝結系數,Fvap=50,Fcond=0.01; αnuc——單位液體所含氣體的體積分數,αnuc=5×10-4; p——飽和蒸汽壓; psat——水壓; R——氣泡半徑,R=1×10-6。 在施肥器邊界條件的設置中,p1、p2、p3分別為施肥器進口壓力、出口壓力以及吸肥口壓力值。進口和吸肥口邊界條件均設置為壓力入口,考慮到施肥器離肥料液面有一定距離,故吸肥口壓力p3設置為-5 000 Pa;本研究基于自循環式實驗裝置[11],對應仿真模型出口邊界為自由出流狀態,因此出口為壓力出口,p2數值為0 MPa;施肥器管壁粗糙度設置為0.03 mm。 為驗證程序有效性,本文對文獻[18]中對稱W1型文丘里施肥器模型(出口壓力p2保持0.1 MPa不變,進口壓力設置為0.18~0.30 MPa,增量為0.01 MPa)吸肥量的數值計算進行重復,本文所得計算結果(圖2)與文獻的計算結果相比最大相對誤差為6.46%,誤差在可接受范圍之內,表明數值模擬方法的可靠性。 圖2 程序有效性驗證Fig.2 Program validation 本文采用結構化六面體網格對計算流域進行離散,并對吸肥腔與喉管處進行加密處理。為保證計算結果準確可靠,進行了網格無關性驗證。選擇四種網格數量:0.9×105、1.1×105、1.3×105、1.5×105,對同一問題(入口:0.6 MPa、出口:0 MPa、吸肥口:-5 000 Pa)進行對比計算,計算所得吸肥量與網格量的關系如圖3所示,綜合考慮計算的準確性以及計算量的大小,最終采用1.5×105的網格進行相應的數值計算。 圖3 網格無關性驗證Fig.3 Grid-independent verification 為強化射流式施肥器的吸肥性能,本文基于文獻[10]中射流式施肥器模型,研究了不同噴嘴長度對施肥器性能的影響。噴嘴長度分別選取L、3L/4、L/2、L/4以及0的5種情況。圖4(a)、圖4(b)和圖4(c)分別對應噴嘴長度為0、L/2和L時的施肥器結構,以及局部放大的三維噴嘴結構。相應的結構尺寸見表2。 表2 噴嘴結構尺寸Tab.2 Nozzle structure size (a) 噴嘴長度0 射流式施肥器的基本性能指標包括有吸肥量q、吸肥濃度θ、進口流量比M和吸肥效率η,計算如式(8)~式(10)所示。 (8) (9) (10) 式中:Q——進口流量,m3/h。 本文首先研究了進出口壓差ΔP對吸肥量的影響規律,計算中施肥器出口壓力保持為0 MPa,進口壓力設置范圍為0.1~1.0 MPa(增量為0.1 MPa)。圖5是噴嘴長度為L時射流式施肥器吸肥量與進出口壓差的關系曲線圖。從圖5中可以看出,隨著進出口壓差的不斷增大,施肥器的吸肥流量表現為先快速增加后趨于平緩的趨勢。在進出口壓差為0.1~0.5 MPa范圍內,施肥器的吸肥量隨著進出口壓差的增大近似于線性增長;當進出口壓差為0.5 MPa時,吸肥量出現拐點,隨著進出口壓差的繼續增大,噴嘴長度為L的射流式施肥器吸肥量基本保持在1.49 m3/h不再明顯增加;這表明在進出口壓差達到0.5 MPa之后施肥器內部水力損失增大,導致吸肥量無法進一步提升。本文數值計算結果與文獻[10]中射流式施肥器的吸肥規律一致,說明了本文所使用數值模型的可靠性。 圖5 進出口壓差對吸肥量q的影響關系曲線圖Fig.5 Influence of differential inlet and outlet pressure on the amount of fertilizer absorbed 為強化施肥器吸肥性能,本文對比研究了不同進出口壓差條件下(0.6~1.0 MPa),五種不同噴嘴長度對施肥器性能的影響,相應的影響關系曲線如圖6所示。 (a) 吸肥量 圖6(a)為不同進出口壓差下噴嘴長度對吸肥量的影響曲線。可以看出,噴嘴長度不變的條件下,隨著進出口壓差的增加施肥器的吸肥量均有所增大,其中噴嘴長度為L時,吸肥量增長較小。而不同進出口壓差條件下,隨著噴嘴長度的增加,施肥器吸肥量近似單調遞減,噴嘴長度為L時吸肥量達到最低。進出口壓差數值反映了主管流道在施肥器工作過程中的壓力損失,當進出口壓差為1.0 MPa時,定量分析得到噴嘴長度為0、L/4、L/2和3L/4相對于噴嘴長度L的吸肥量分別提高了21.01%、20.14%、17.67%以及11.67%。研究結果表明,在相同的壓力損失條件下,噴嘴長度較小的施肥器的內部壓能相較于長噴嘴的施肥器能更好地轉化成肥液動能。 圖6(b)和圖6(c)分別為噴嘴長度對施肥器吸肥濃度和進口流量比的影響曲線。可以看出,進出口壓差逐漸增加時,不同噴嘴長度條件下的施肥器吸肥濃度和進口流量比均呈遞減變化;而進出口壓差不變的條件下,隨著噴嘴長度的增加,射流式施肥器的吸肥濃度和進口流量比的變化趨勢相似,均為先增大后趨于下降,并在噴嘴長度為L/2和3L/4之間存在峰值,而在噴嘴長度為L時為最小。圖6(d)表明噴嘴長度對吸肥效率的影響相對較小。由其計算公式可知,吸肥效率與進口流量比成正相關,因此噴嘴長度對吸肥效率的影響曲線與其對進口流量比的影響曲線的特征相似;在相同進出口壓差條件下,隨著噴嘴長度的增加,吸肥效率總體先緩慢增加后下降。 綜上所述,吸肥腔內部的噴嘴長度會對施肥器的吸肥性能產生顯著影響。噴嘴長度過長會影響射流式施肥器的吸肥性能,不同進出口壓差下,噴嘴長度為L施肥器在吸肥濃度、進口流量比和吸肥效率幾方面的性能指標均為最低;且當進出口壓差為1.0 MPa時,較小噴嘴施肥器的吸肥量均比噴嘴長度為L的吸肥量多10%以上。 本文進一步對施肥器內部流場進行分析,以揭示噴嘴長度對施肥器性能影響的機制。基于以上研究結果,本文對進出口壓差為0.6 MPa時,噴嘴長度為0、L/2和L的施肥器內部流場特性進行對比分析。 圖7為噴嘴長度為0、L/2和L的射流式施肥器z=0截面上的靜壓分布圖。從圖7(b)中可以看出,噴嘴長度為L/2條件下的吸肥腔內部的負壓分布區域面積最大(圖中箭頭所示位置,即吸肥管道與喉管入口相交處),噴嘴長度為0條件下的負壓分布區域面積次之(圖7(a)),而噴嘴長度為L時的負壓分布面積最小(圖7(c))。射流式施肥器中,吸肥腔負壓區域的壓能可轉化為肥液動能,負壓分布的大小決定了吸肥能力的大小;而噴嘴長度為L時吸肥腔內負壓面積最小,這是其吸肥量較低的一個主要原因。 (a) 噴嘴長度0 通過對圖7中喉管和擴散段的觀察發現,三種施肥器的負壓區域(壓力數值接近或達到飽和蒸氣壓)均從喉管入口處開始沿著流道向下延伸;相比之下,噴嘴長度為L時的負壓區域延伸范圍最廣,直至擴散段前端。在施肥器中,當局部壓力低于飽和蒸氣壓時,水體中相應區域因空化而不斷產生空泡,空泡數量的增加則會影響施肥器的內部流態,進而影響其吸肥性能。這是噴嘴長度為L的施肥器吸肥性能較低的另一個因素。 為明確空化現象對吸肥量的影響,本文對噴嘴長度為0、L/2和L的射流式施肥器內部的空化現象進行了分析。圖8描述了施肥器內不同喉管位置處(即x=5 mm、10 mm、15 mm、20 mm、25 mm截面)的氣相體積分數分布情況。氣相體積分數是氣相在氣液混合物中所占的體積分數,可反映候管部空化的分布情況。氣相體積分數數值越大則意味著在該區域的空化強度越大。 (a) 噴嘴長度0 從圖8(a)和圖8(b)可以看出,噴嘴長度為0和噴嘴長度為L/2時,施肥器空化區域僅存在于喉管開始位置,且為環狀空泡薄膜。而噴嘴長度為L的施肥器內的環狀空化不僅在喉管開始位置出現,而且緊貼著喉管壁面形成環狀空化并沿主流向下延伸,且向下游不斷增厚直至擴散段前端,如圖8(c)所示。根據文獻[15]報道,射流泵中空泡群受到回射流影響在擴散段中脫落,會堵塞整個流道,制約被吸流體流量。研究結果表明,噴嘴長度為L時,吸肥器內空化程度最為劇烈,氣液兩相之間的能量交換越頻繁,其會制約吸肥量的增加,因此,相應的吸肥性能指標最低。 通過對射流器內部流場分析可知,不同噴嘴條件下,施肥器內部的負壓分布,相應的空化現象及其占比,是影響射流式吸肥器吸肥性能的主要原因。 1) 射流式施肥器吸肥量隨著進出口壓差的增大而增大,當壓差到達一定數值后,吸肥量不再明顯增加;噴嘴長度為L的施肥器進出口壓差的拐點為0.5 MPa。 2) 噴嘴長度對射流式施肥器的吸肥性能有顯著影響。進出口壓差為0.6~1.0 MPa條件下,噴嘴長度為L的施肥器的吸肥濃度、進口流量比和吸肥效率幾個方面性能指標均最低;且當進出口壓差為1.0 MPa時,相較于噴嘴長度為L的條件,其他較小噴嘴長度的施肥器的吸肥量均提高10%以上。 3) 通過對射流器內部流場分析可知,不同噴嘴條件下,施肥器內部的負壓分布,相應的空化現象及其占比,是影響射流式吸肥器吸肥性能的主要原因。本研究可為射流式施肥器的設計提供相應的理論支撐。2 程序和網格有效性驗證
2.1 程序有效性驗證
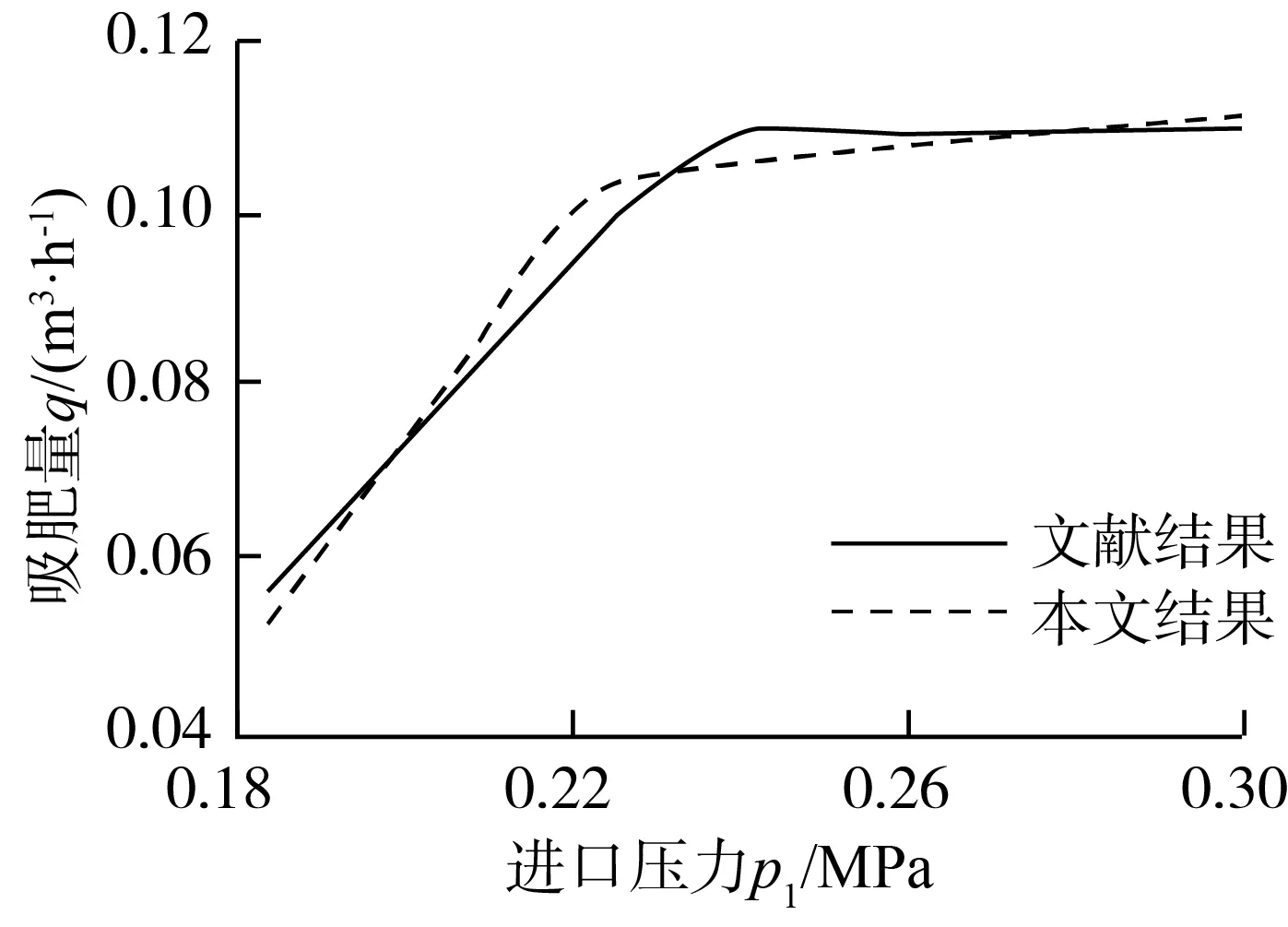
2.2 模型有效性驗證
3 結果與分析
3.1 結構及幾何參數

3.2 進出口壓差對吸肥量影響規律研究

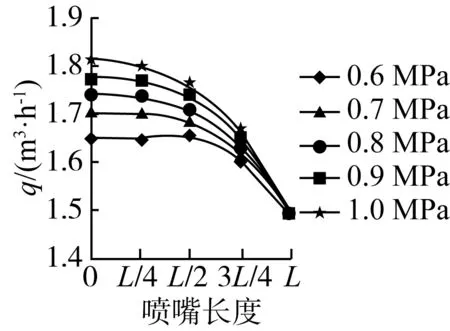
3.3 噴嘴長度對吸肥性能影響規律研究
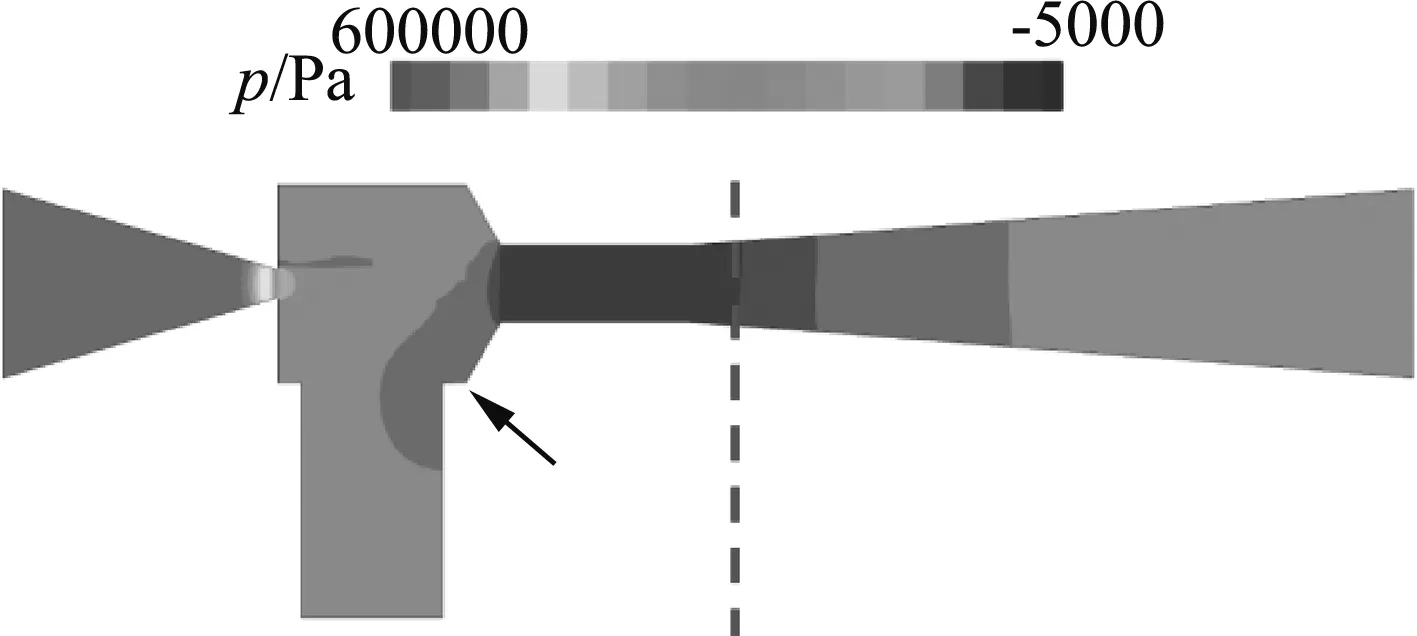
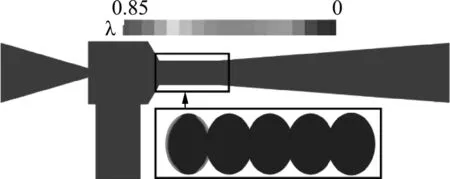
3.4 施肥器內部流場分析
4 結論

