以數線促進估算的理解

王小蓮

【摘? ?要】數線，即表征數的意義、性質和運算的線，是一種教學輔助工具。求小數近似數的難點在于四舍五入，它從整數的區間數判斷走向了較為抽象的小數區間數判斷。教學中，教師創造性地利用數線表征數的意義，用多維視角理解估算，用數形結合的方法促進學生對小數估算的理解，發展學生的數感，也為學生后續建立整數、分數、小數等不同數系之間的聯系積累活動經驗。

【關鍵詞】小數近似數；數線；估算；表征

【課前思考】

數線，即表征數的意義、性質和運算的線，是一種教學輔助工具。利用數線估計是解決日常生活中常見問題的一種數學能力，能幫助學生理解相應的知識內容。近似數和估算教學的關鍵有兩點：一是從確切的數擴充到表示范圍的區間；二是根據實際情況確定范圍。［1］人教版教材四年級下冊在編排“小數的近似數”這一內容時，以“求小欣身高的近似數”這一現實問題引入，接著出示“求一個小數的近似數，同求整數的近似數相似”這一遷移性結論，并直接給出四舍五入求近似數“看尾數首位，即省略的尾數部分最高位上的數”［2］的方法性結論。這樣的編排方式重視方法的指導，卻忽視了原理的理解。因此，學生在學習時易出現以下難點：一是為什么保留兩位小數，要看千分位；二是在表示近似數時，小數末尾的0為什么不能去掉。

基于上述問題，筆者進行了整數近似數的調研。調研發現，學生雖然能正確解答，卻說不清楚“四舍五入到萬位要看千位”的道理。這一現象暴露出學生對整數近似數的理解并不深刻。“為什么可以用四舍五入法求小數的近似數？保留一位小數，為什么只要看百分位就可以了？在表示近似數時，小數末尾的0為什么不能去掉？”［3］在針對五年級學生（學習過小數的近似數）的訪談中，學生對這些問題一臉茫然。由此可見，學生在近似數原理的自然遷移上具有一定困難。

那么，如何才能讓學生更好地理解近似數，并能運用近似數解決問題呢？針對這一教學難點，教師可創造性地運用具象的數線，化抽象為形象，引導學生通過數線觀察，將整數的四舍五入近似法則遷移到小數中；通過數線對比，解決“看尾數首位”這一關鍵難點，深刻理解“四舍五入”求小數近似數的方法；通過數線推理，深刻理解精確度，體會近似數背后的區間思想，發展學生的測量和數感等數學能力。

【教學目標】

1.能夠根據要求用“四舍五入法”保留一定的小數位數，求出小數的近似數。

2.在對數線模型的探索中歸納求小數近似數的方法，體會近似背后的區間思想，理解在表示近似數時小數末尾的0不能去掉的本質。

【教學重難點】

借助直觀數線，掌握用“四舍五入法”求小數近似數的方法。理解保留的位數不同，求得近似數的精確度也不一樣。

【教學過程】

一、觀察數線，理解為什么要和中間數進行比較

1.經驗回溯：求整百數近似數的方法

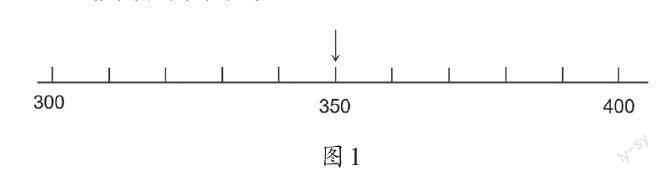
教師出示圖1。

師：在圖1這條數線中，哪些數接近300？哪些數接近400？你是怎么想的？

生：30?、31?、32?、33?、34?這些數接近300；35?、36?、37?、38?、39?更接近400；350正好在中間。

生：十位比5小就接近300，十位比5大就接近400。

師：原來，我們只要看十位就能知道這個數是離300近還是400近。

2.方法回溯：求整十數近似數的方法

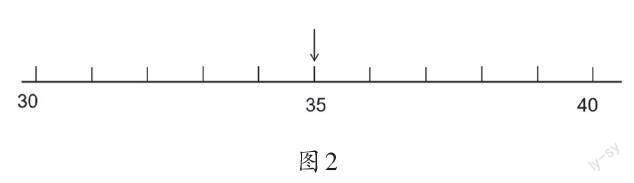
教師出示圖2。

師：在圖2這條數線中，哪些數接近30？哪些數接近40？你是怎么想的？

生：個位比5小就接近30，個位比5大就接近40。

生：只要把這個數和35進行比較就可以了。

師：請大家觀察這兩條數線，判斷數字的近似數時，是和誰進行比較？

生：只要和中間的數35或350進行比較，就能快速判斷它的近似數。

師：我們在求一個數的近似數時，都是把這個數和中間的數進行比較，這個方法就是“四舍五入法”，而且中間的數也是要“五入”的。

評析：求小數的近似數和求整數近似數的方法相近，都是用“四舍五入法”。但隨著數域的擴大，學生在小數范圍內應用“四舍五入法”有一定難度。與教材直接給出遷移性結論相比，上述環節的設計能為將“四舍五入法”從整數遷移到小數提供直觀支持。它承接了整數范圍內求近似數的經驗，利用觀察數線的活動，探究“哪些數更接近”“判斷近似數時是和誰進行比較”的關鍵問題，從而連接“舍”“入”和“遠”“近”。學生通過數線上中間數的分段，感知求一個三位數的近似數要關注十位，求一個兩位數的近似數要關注個位。以求整百數近似數的方法為例，十位是0～4對應“四舍”，十位是5～9對應“五入”，直觀形象地對“四舍五入法”進行了遷移。

二、對比數線，理解“為什么要看尾數首位”

1.保留到整數，為什么只看十分位

師：老師的身高是1.69米，保留整數是多少？

生：1.69比1大，比2小，保留整數可能是1或2。

生：1.69離1遠，離2近，所以1.69保留整數是2。

教師出示圖3，圖中的數線將1和2之間的線平均分成了10份。

師：觀察圖3中的數線，我們在判斷1.69離誰近時其實是將它和誰進行比較？

生：我是把它和1.5進行比較。比1.5大就接近2，比1.5小就接近1。1.69在1.5的右邊，更接近于2。

師：比較1.69和1.5時，整數部分都一樣，關鍵是比較什么？

生：保留整數時，1.69和1.5的整數部分都一樣，只要將十分位上的6和5進行比較即可。6比5大，所以1.69約等于2。

生：我還發現在精確到個位時，不用看百分位和千分位，只要將十分位進行四舍五入就可以了。

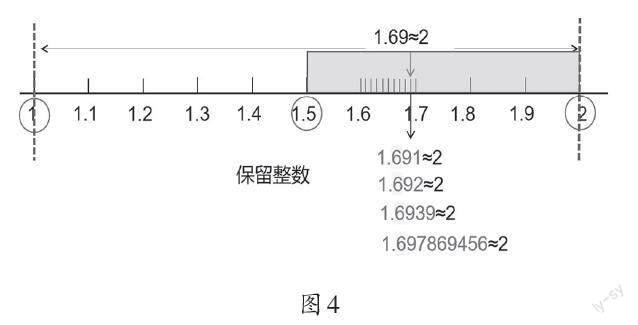
教師用課件動態演示圖4，并追問。

師：那1.691保留整數呢？1.692呢？1.6939呢？1.697869456呢？你有什么發現？

生：只要十分位上的數比5大，精確到個位都是2。

師：到底是哪個數位上的數決定了保留整數都約等于2？

生：是由十分位上的6決定的。

師：只要十分位上的數比5大，不管后面數位上的數是幾，對最后的結果都沒有影響，在保留整數時都約等于2。所以，保留整數只需看十分位。

2.保留一位小數，自主探索求近似數的方法

師：那將1.69米保留一位小數會是多少？把你的探究過程記錄在數線上。

學生獨立思考，并將探究過程記錄在作業紙的數線上。

生：我是將1.6和1.7之間的格子再平均分成10份，找到1.69，發現1.69在1.6和1.7之間，離1.6遠，離1.7近，所以1.69保留一位小數是1.7（如圖5）。

生：我是把它和1.6與1.7中間的1.65進行比較，比1.65大就接近1.7，比1.65小就接近1.6。

師：你們在比較1.69和1.65時，關鍵是在比較什么？

生：保留一位小數時，關鍵要比較百分位上的9，9比5大，所以1.69約等于1.7。

師：那1.691保留一位小數呢？1.692呢？1.6939呢？1.697869456呢？觀察這些數據，到底是哪個數位上的數決定了它們在保留一位小數時都約等于1.7呢？

生：這些數的百分位都是9，其實只要百分位上的數大于或等于5，不管千分位、萬分位上的數是幾，這些數在保留一位小數時都約等于1.7。

師：所以在保留一位小數時，只需要將百分位四舍五入就可以了。

3.保留兩位小數，遷移應用求近似數的方法

師：通過精準測量，老師的身高是1.697米，現在不看數線圖，根據剛才的經驗，你知道怎么保留兩位小數嗎？

生：1.697保留兩位小數在1.69和1.70之間，千分位是7，離1.70更近，所以1.697保留兩位小數約等于1.70。

生：保留整數要看十分位，保留一位小數要看百分位，那么保留兩位小數就要看千分位。將千分位四舍五入，7大于5，所以1.697約等于1.70。

師：看來，求整數近似數的方法在求小數近似數時同樣適用，都需要用“四舍五入法”保留一定的小數位數。

評析：教師將數線不斷均分，以具體的形助力學生對抽象的數區間的理解，引導學生明白將一個小數保留到整數只要和十分位上的5進行比較，再利用“四舍五入法”進行判斷即可。教師先提供多組數據，不斷向學生追問，讓學生理解不管是三位小數還是更多位數的小數，將它們保留一位小數只需看百分位上的數。接著利用學生第一次的比較經驗，開展保留一位小數和兩位小數的說理探究，讓學生在數線的“遠近模型”中形成求近似數要看尾數首位的推理判斷經驗，用數線感悟小數區間數范圍，完善對保留小數位數的原理的探究。

三、利用數線，理解“小數末尾的0為什么不能去掉”

1.借助數線表征，尋找近似區間

師：剛才將1.697米保留兩位小數時，出現了兩種答案：1.7米和1.70米。你們同意哪種答案？為什么？

生：我認為都對，1.7和1.70都表示1米7分米，答案是一樣的。

生：我認為不對，因為1.7是一位小數，而我們需要保留兩位小數。

師：大家有不同的意見，那到底哪種說法對呢？請你在數線上找一找、畫一畫，并把你的想法和同桌進行交流。

學生先在作業紙（如圖6）上獨立完成，再和同桌交流。

生：一個數保留一位小數后是1.7，所以關鍵要看百分位。百分位上可能是1、2、3、4，那么這個小數可能是1.7到1.74之間的數。

師：在1.7的右邊，你找到了4個近似數是1.7的兩位小數。那么在1.7的左邊有這樣的數嗎？

生：在1.7的左邊還有1.69、1.68、1.67、1.66、1.65。

師：利用將百分位四舍五入的方法，你們在數線上找到了近似數是1.7的兩位小數，那么這個數有可能是三位小數嗎？

生：它還可能是1.701、1.712、1.734、1.748……

師：為什么這些小數保留一位小數也是1.7？這樣的數還有多少個？我們一起把這些數的范圍畫出來。

教師用課件動態演示圖7。

生：近似數是1.70，說明是要把這個數保留兩位小數，所以要看千分位上的數。我在數線上找到了1.695、1.696、1.697、1.698、1.699、1.700、1.701、1.702、1.703、1.704這些三位小數。

生：除了這些三位小數，只要大于等于1.695，小于1.705，不管是幾位小數，它保留兩位小數的近似數都是1.70。

教師用課件動態演示圖8。

2.合并表征結果，對比精確區間

教師用課件動態演示，合并圖7、圖8，得到圖9。

師：剛才我們通過數線的推理，找到了近似數是1.7和1.70的小數范圍，仔細觀察，它們一樣嗎？

生：1.70的近似范圍要比1.7的近似范圍小得多，它們是不一樣的。

師：想象數線，1.700的近似范圍在哪里？1.7000的呢？你有什么發現？

評析：教師借助數線幫助學生建立起“小數末尾的0代表這個近似數的精確程度”的直觀模型，緊扣“一個數的計數單位越小，它的精確程度就越高”的意義本質。在準確數和近似數的比較中，數概念的學習從一個確定的數擴展到一個區間，這也是數感的表現之一。一個小數的近似數同樣和計數單位有關，一個數的計數單位越小，它的精確度就越高。［4］通過數線中精確區間的直觀呈現，學生理解了去掉小數末尾的0會直接影響數的精確度和對應區間數。

【教學反思】

一、從數線感悟小數區間數的范圍，完善對保留小數位數的原理探究

四舍五入求近似數“看尾數首位”的結論性方法對學生來說難度很大。教學中，教師除了要利用整數“四舍五入法”進行自然遷移，還要引導學生探究為什么保留一位小數就要把百分位上和后面的數都省略，即“為什么只要看百分位”“小數尾數為什么可以去掉”等問題。教學時，教師借助數線，化抽象為具體，緊扣核心概念“計數單位”，促進學生對小數意義的理解，通過學生熟悉的活動，引導學生直觀看到小數最接近的數，利用小數區間范圍的數理解“看尾數首位，即省略的尾數部分最高位上的數”進行四舍五入的原因，完善對小數位數原理的探究。

二、從數線感知數與距離的關系，完善對小數意義教學的整體建構

精確數是一個點，而近似數是靠近精確數的一段范圍內所有點的集合。教師可引導學生利用數學的均分特征，找到相應小數所在位置與起點和終點的距離，在數線的“遠近模型”中，形成求近似數要看尾數首位的推理判斷能力，積累經驗，更加深入形象地理解小數的意義；在利用數線和創作數線的過程中建構模型，促進數線的產生，感受計數單位的細分，從而完善對小數意義的整體建構。

參考文獻：

［1］章勤瓊. 3.8是3.80的近似數嗎：近似和估算教學的關鍵是什么［J］. 教學月刊·小學版（數學），2019（4）：60-63.

［2］朱紹敏.數形結合 直觀感悟：數線解決四舍五入求近似數看尾數首位問題［J］.小學教學設計，2017（11）：25-26.

［3］張雅芬.巧借數軸 探其本質：“求小數的近似數”片段賞析［J］.數學學習與研究，2015（19）：87，89.

［4］吳正憲，張秋爽.整體把握教材 突出數概念本質：“小數的意義和性質”單元教學思考［J］.小學教學（數學版），2020（5）：25-27.

（浙江省溫州市龍灣區教師發展中心）