基于ICEEMDAN和松鼠算法優化極限學習機的滾動軸承故障診斷
周 陽,趙鳳強,喬 浩,王 波,史書杰
(大連民族大學 機電工程學院,遼寧 大連 116650)
滾動軸承作為旋轉機械的核心組成部分,起著承受載荷、傳遞動力的重要作用,其穩定性和可靠性是整個設備健康工作的關鍵。根據統計,滾動軸承故障造成的旋轉機械設備故障占所有機械故障的30%[1]。當滾動軸承發生故障時,通常會有異常的振動噪聲和異常的溫升,振動噪聲會影響機械設備的正常運轉,并且嚴重時會造成重大事故;而溫升過高會導致軸承過早損壞或降低軸承壽命,所以精準識別與判斷軸承故障是保持機械設備長久運營的關鍵。工作時,軸承有無故障都會產生一定的振動信號,經過多年的技術發展,提取振動信號中的有效特征信號和分析軸承故障原因的方法也逐漸多樣化、高效化。
在處理非平穩,非線性的振動信號時,經驗模態分解(EMD)是強有力的工具[2],復雜的信號集可以通過該方法自適應分解為若干分量和殘差,即固有模態函數(IMF)。EMD有很好的自適應能力和信噪比[3],能夠從瞬時頻率中提取重要信息,鮑懷謙[4]為增強傳統軸承強噪聲背景下故障診斷精度和穩定度,用EMD處理振動信號,有效地提取到前期的微弱信號,更好地識別軸承故障特征。然而,經驗模態分解也存在著一些缺陷,當采集到的信號存在強噪音干擾,脈沖干擾等異常事件或者信號分量頻率和幅值之間相互作用,就會發生模態混疊,從而影響了IMF的信號特征。同時,在由極值點確定包絡線的過程中,存在端點被當做極值點的情況,從而產生較大的計算誤差,引發端點效應問題,導致產生虛假分量和失真現象。為此,集合經驗模態分解(EEMD)[5]、互補經驗模態分解(CEEMD)[6]、完整集合經驗模態分解(CEEMDAN)[7]等EMD的改進算法依次被提出。Jinde Zheng[8]也提出了均值優化模式分解(MOMD)方法,以提高原始EMD在均值曲線構建中的性能,結果表明,MOMD方法比原始EMD方法獲得了更準確的IMF分量和故障診斷效果。改進的自適應噪聲完備集合經驗模態分解(ICEEMDAN)是2014年由Colominas[9]提出的,在重構信號時,它能消除噪聲影響從而避免信號被污染,同時能夠有效克服模態混疊和端點效應問題[10]。
在模式識別方面,常用的方法有隨機森林[11]、支持向量機(SVM)[12]、人工神經網絡(ANN)[13]、極限學習機(ELM)[14]等,相對于其他方法,極限學習機具有學習效率高、參數設定簡單、泛化性好等優點。董治麟[15]將多尺度排列熵與ELM結合,應用于對滾動軸承故障類型和程度進行識別,相對于其他方法具有更高的識別率。同時,ELM是一種單層前饋神經網絡,算法參數少,訓練時間快,但其輸入權值和隱含層閾值對分類精度有較大的影響。本文為提高ELM的識別準確率和泛化能力,選擇適合的網絡參數,提出松鼠搜索算法優化極限學習機SSA-ELM的模式識別方法。
1 特征提取方法
1.1 ICEEMDAN原理
在 ICEEMDAN算法中,分解過程的每個階段,把白噪聲一步步地加入,與此同時,在 EMD分解白噪聲所得的模態中,選出特殊的模態信號,并將其添加到殘差信號中,從而得到信號的每一模態分量,實現對原始信號的完全分解[16]。
ICEEMDAN有以下算子Ek(·)、M(·)、〈·〉,Ek(·)表示經過EMD分解得到的第k個模態分量,M(·)是生成局部平均值運算符,〈·〉表示求平均值,具體實現步驟如下:
(1)對原始信號x加入經過EMD分解的具有零均值和單位方差的高斯白噪聲分量,根據xi=x+β0E1(ωi)得到分解序列的局部均值信號為M(x+β0E1(ωi)),其中,β0為第一個噪聲振幅,ωi表示被添加的第i個白噪聲。
第一個殘差:
r1=〈M(xi)〉 (i=1,2....S)。
(1)
第一個分量:
IMF1=x-r1。
(2)
對第一個殘差r1加入白噪聲作為第二次局部平均值M(r1+β1E2(ωi))可以得到第二個分量:
IMF2=r1-r2=r1-〈M(r1+β1E2(ωi)) 〉。
(3)
以此類推,直到不能分解為止,得到第K個分量:
IMFK=rK-1-rK=rK-1-〈M(rK-1+βK-1EK(ωi)) 〉。
(4)
式中,噪聲振幅βk由以下公式確定:
(5)
式中,εk為第k次加噪信號與分析信號間的期望信噪比倒數,std為標準差。
可以看出,ICEEMDAN算法的核心依然是經驗模態分解,與CEEMDAN向信號分解的每一個階段都加入高斯白噪聲不同,它先利用EMD將自適應高斯白噪聲分解,獲取其中特定第K個IMF分量作為輔助噪聲,接著對IMF分量計算信號和噪聲的局部均值并把殘差減去局部均值,最后得到K階差值,計算過程中,噪聲信號和偽分量也大大減少。因此ICEEMDAN能有效地避免重構誤差、模態混疊等問題,其流程圖如圖1。
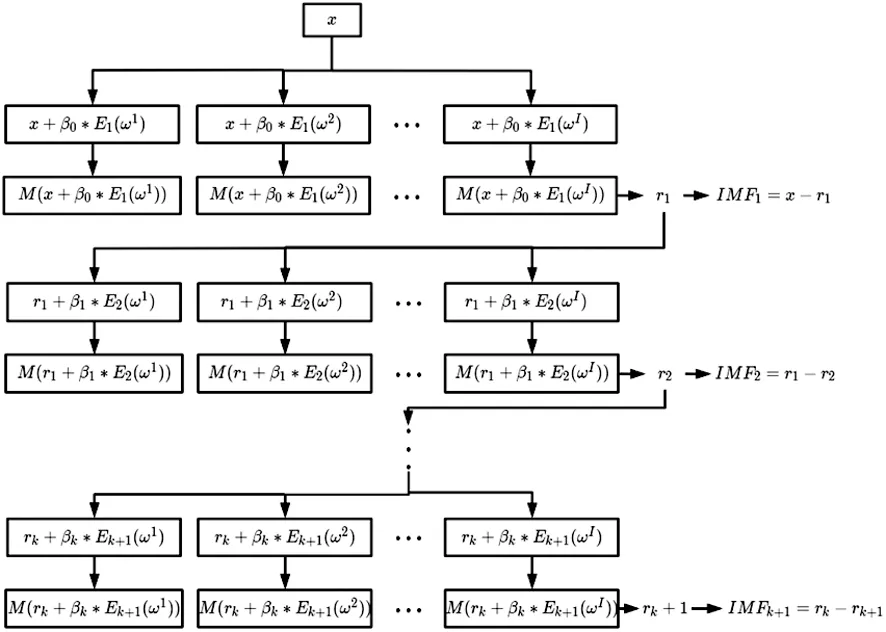
圖1 分解流程圖
1.2 相關系數
由于原始信號中含有大量虛假的分量,相關性較差,不能有效反應原始信號特征,所以在將它分解后可與原始信號的互相關系數作為區分虛假分量的評定指標,并將互相關系數較小的IMF分量剔除。
在時域中,對于容量為n的樣本,兩個信號xi和yi的互相關系數r表示為
(6)
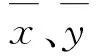
1.3 奇異值分解(Singular Value Decomposition,SVD)
SVD[17]是一種矩陣分解方法,在機器學習、信號處理、統計分析等方面有著廣泛應用。奇異值分解能夠有效獲取矩陣中所代表的重要信息,本文將利用這個特點提取篩選出的IMF分量的特征值。在線性相關的矩陣左右分別乘以一個正交矩陣進行變換,可將原始矩陣轉換為線性獨立的矩陣。例如對于矩陣Bm×n,秩為r,則存在兩個標準正交矩陣U和W及對角矩陣D,滿足
B=UDWT。
(7)
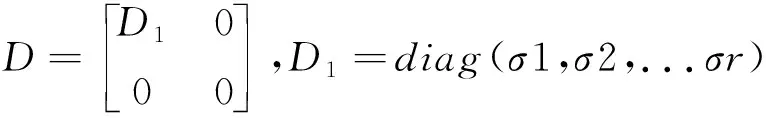
2 故障分類方法
2.1 松鼠搜索算法(Squirrel Search Algorithm,SSA)
在松鼠搜索算法中[18],松鼠的位置分為三種:山核桃樹、橡子樹、普通樹,分別表示最優解,次優解和一般解。松鼠們通過移動位置尋找更好的食物源。具體流程如下:
初始森林中的n只松鼠可以用下面的矩陣表示:
(8)
式中,d為待優化變量的維度,FSi,j表示第幾只松鼠在第j維上的值,由式(9)所確定。
FSi,j=FSiL+U(0,1)×(FSi,u-FSi,L)。
(9)
式中,U(0,1)是0和1之間的隨機值,FSi,u和FSi,L是第j維的上下界。
所有松鼠的適應度函數表示為
(10)
計算排序所有松鼠的適應度值,最佳適應度值的松鼠停留在山核桃樹上,次佳適應度值的三只松鼠停留在橡子樹上,其他的松鼠則停留在普通樹上。接下來根據天敵出現的概率Pdp以及松鼠們所在位置決定對應的三種移動策略。當沒有天敵出現,松鼠可以通過滑行來更好的獲取食物,尋找山核桃樹和橡樹;而存在天敵時,松鼠們會謹慎前行,隨機轉移到一個新的地方。
(1)第一種移動策略是由橡樹去往山核桃樹。
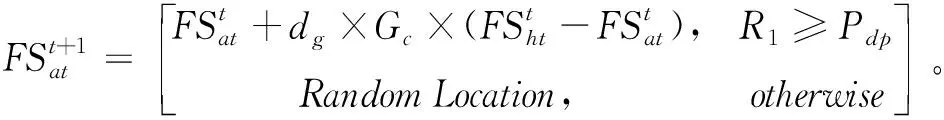
(11)
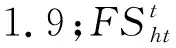
(2)第二種移動策略是由普通樹去往橡樹。
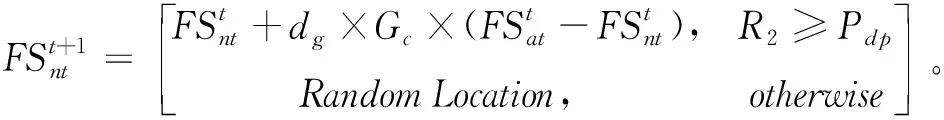
(12)
式中,R2為0和1之間的隨機數。
(3)第三種移動策略是部分已經有過食物的松鼠會由普通樹去往山核桃樹。
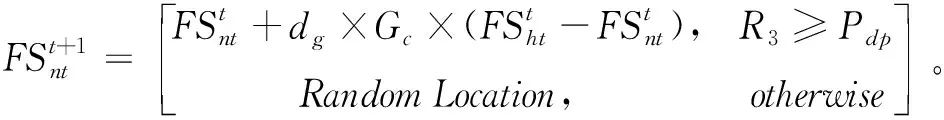
(13)
式中,R3為0和1之間的隨機數。
為了防止陷入局部最優,松鼠優化算法中引入了季節變化機制,通過季節檢測常量Sc檢測季節的變化。
(14)
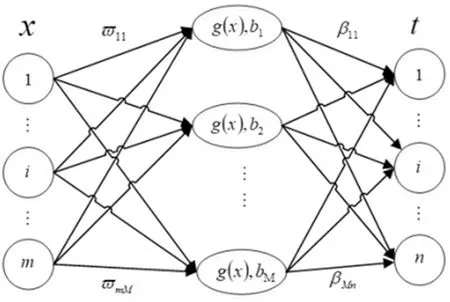
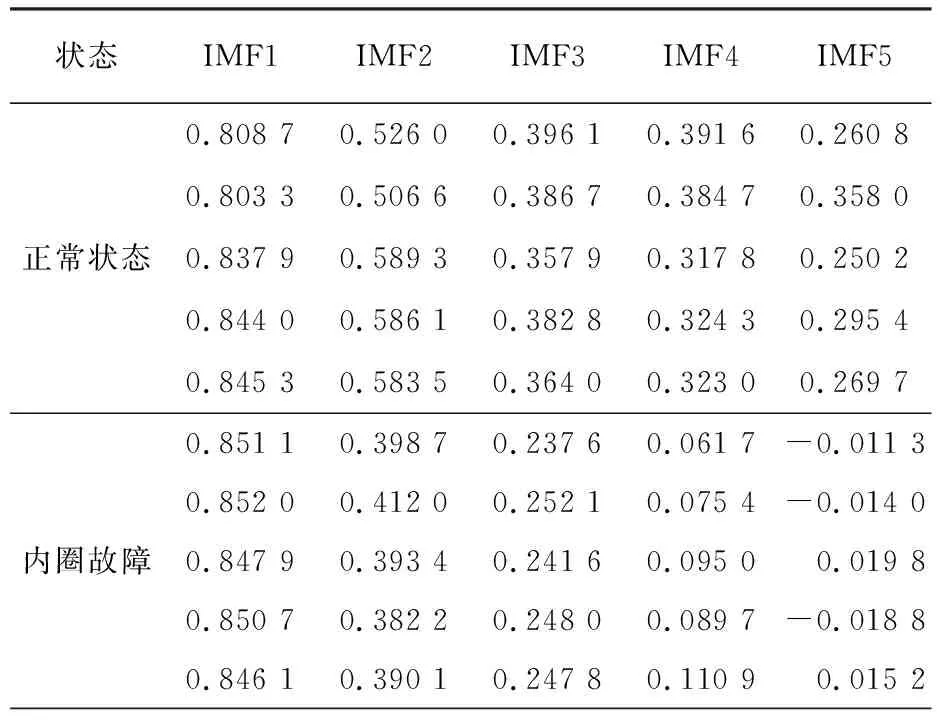
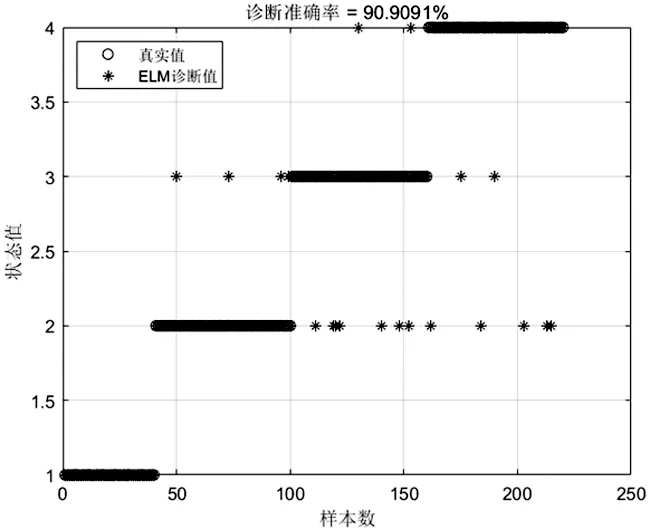
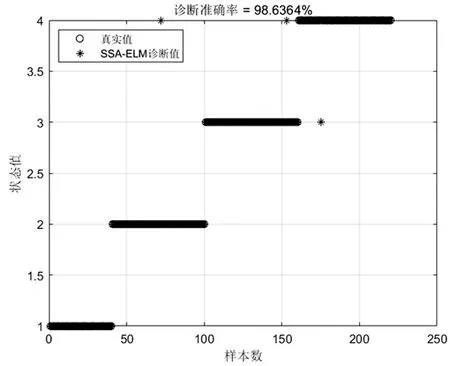
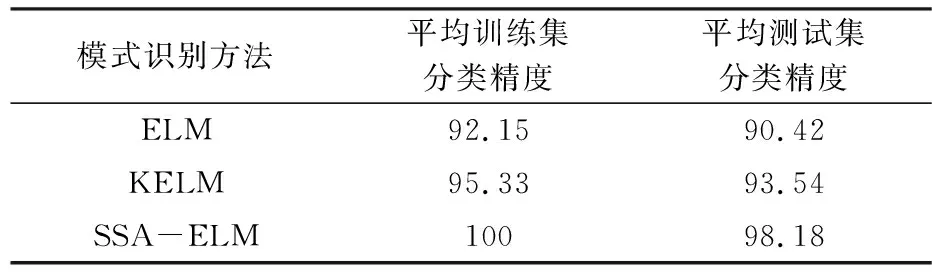
當季節變化條件Sct (15) 式中,Smin主要用于平衡全局和局部搜索能力,t和tm分別為當前迭代和最大迭代值。 當滿足季節變化條件(冬季結束),普通樹上的松鼠就會按照式(16)移動。 (16) 式中,Levy表示列維分布中的步長,列維分布通過隨機改變步長能夠提高全局搜索能力。 (17) 式中,ra和rb是[0,1]間的正態分布隨機數,β為常數,一般取1.5,σ取值如式(18)。 (18) 式中,τ(x)=(x-1)!。 極限學習機(Extreme Learning Machine,ELM)是由Huang[19]等人在2014年提出,它的輸入權值矩陣與隱含層閾值均為隨機生成,只需選擇合適的隱含層神經元個數,與傳統的基于梯度下降的學習算法如反向傳播算法相比,具有訓練參數少、學習速度快、泛化能力強等優勢。目前已被廣泛應用于分類、回歸以及預測問題。 設m、M、n分別為ELM網絡輸入層、隱含層和輸出層的節點數,g是隱層神經元的激活函數,bi為閾值。 設有N個任意數據樣本(xi,ti),1≤i≤N,其中: xi=[xi1,xi2,…,xim]T∈Rm; (19) ti=[ti1,ti2,…,tin]T∈Rn。 (20) ELM模型如圖2。 圖2 極限學習機的網絡訓練模型圖 數學表達式為 (21) 式中:βi=[βi1,βi2…,βin]T為第i個隱層節點與輸出權值向量;ωi=[ω1i,ω2i,…ωmi]T為輸入層節點與第i個隱層節點的輸入權值向量;oi=[oi1,oi2,…,oin]T為最終輸出值。 ELM算法用于故障分類時,有兩個決定模型訓練性能和最終分類準確率的關鍵因素,便是初始輸入權值ωi和隱藏層閾值bi。為了減小這兩個參數給診斷精度帶來性能和精度的影響,本文采用SSA算法對ELM兩個參數進行迭代尋優,進而建立SSA-ELM分類模型。 SSA優化ELM流程圖如圖3。以訓練集錯誤率作為適應度函數,即當錯誤率最小時,所對應的ωi和bi,作為該模型的最優參數。具體優化步驟如下[20]: 圖3 優化模型流程圖 步驟1:設置初始化參數,包括迭代次數、升力系數、天敵出現概率、種群大小等; 步驟2:按初始適應度值劃分食物等級,適應度值最佳的為山核桃樹,其次接下來三個為橡樹,其他為普通樹; 步驟3:根據是否出現天敵,橡樹上的松鼠利用式(11)開始移動,更新位置; 步驟4:普通樹上未有食物的松鼠利用式(12)開始移動,更新位置; 步驟5:普通樹上已有食物的松鼠利用式(13)開始移動,更新位置; 步驟6:將此時所有松鼠得到的最佳適應度值與上一次做對比,更新最佳適應度值并將它們分配到山核桃樹、橡樹和普通樹上; 步驟7:判斷季節變化,如果滿足就改變普通樹上松鼠的位置; 步驟8:根據公式(15)更新Smin值; 步驟9:排序新的適應度值,根據排序結果再次分配松鼠位置; 步驟10:判斷是否達到迭代次數,達到就退出循環并輸出最佳值,否則返回步驟2繼續運行。 本文實驗數據采用凱斯西儲大學軸承數據集部分數據[21],實驗平臺如圖4。該平臺擁有一個2馬力的電機(左)、一個扭矩傳感器(中)、一個功率測試計(右)以及相應的電控設備。被測試軸承廠商為SKF軸承和等效的NTN軸承。其中,SKF軸承會被電火花加工技術在軸承的內圈、外圈、滾動體位置制造出0.007英寸、0.014英寸、0.021英寸的單點故障;TNT軸承則被制造出0.028 英寸和0.040英寸的單點故障。測試中采用的加速度傳感器通過16通道的記錄器記錄振動信號,分別放置于驅動端和風扇端采集,采樣頻率為12 kHz和48 kHz兩種。 圖4 西儲大學軸承實驗平臺 本文選用采樣頻率為12 kHz、負載為0、轉速為1 797 r·min-1的驅動端數據,其中包含了正常狀態和內圈故障、外圈故障、滾動體故障三種故障狀態,以及故障狀態下直徑為0.007、0.014、0.021英寸的三種故障尺寸。將上述的9種故障狀態與正常狀態共計10種類型作為實驗樣本數據,實驗樣本每個序列長度為2 048,正常狀態分為100組數據(數字1作為其狀態值),故障狀態分為450組數據,每種故障有150組(數字2作為內圈故障狀態值、數字3作為外圈故障值、數字4作為滾動體故障值),每個故障狀態都囊括三種尺寸并打亂順序,以3:2的比例分為訓練集和測試集,具體數據見表1。 表1 實驗樣本表 使用ICEEMDAN對樣本集信號進行分解,得到的正常狀態及其IMF分量時域圖如圖5。 圖5 正常狀態信號分解圖 經過ICEEMDAN,原信號被分解出為若干IMF分量,這其中包括一些虛假分量,不利于信號分析。根據相關系數法,選取相關程度較高、能夠明顯反映信號特征的分量。軸承正常狀態下的11個IMF分量與原始信號的相關系數如圖6。經過多次測試發現,系數最高的前5個分量能夠較好地表示原信號特征。 圖6 正常狀態分量的相關系數圖 對選出的IMF分量進行奇異值求解,每種狀態可由5個奇異值(即特征值)表示,每種故障狀態都包含三種尺寸故障,把狀態值與特征值列表歸類,部分數值見表2。 表2 軸承工作下四種狀態的部分特征值 本文將分別使用極限學習機、核極限學習機(KELM)和松鼠有算法優化的ELM對訓練集中各狀態的特征值進行訓練,其中,極限學習機的參數設置:隱含層個數為20,傳遞函數為Sigmoid函數;核極限學習機的參數設置:核函數為徑向基函數(RBF);松鼠算法的參數設置:種群數量為30,最大迭代次數為100,天敵出現概率0.1,滑動系數為1.9,以訓練集錯誤率為適應度值。 利用這三種方法對測試集分類,單次診斷結果如圖7~ 9。 圖7 極限學習機單次診斷圖 圖7中可以看出僅用極限學習機方法分類識別,準確率只有90.909 1%,軸承的外圈故障,內圈故障,滾動體故障識別精度均有較大的誤差。圖8中可以看出核極限學習機分類準確率為93.181 8%,比ELM提高了大約2.272 7%,誤差主要集中在軸承內圈故障和滾動體故障的識別分類上,外圈故障僅有2組診斷失敗。圖9看出經過松鼠算法優化后的極限學習機分類準確率98.636 4%,比ELM提高了7.727 3%,失敗樣本僅外圈故障、內圈故障和滾動體故障各一例。 圖8 核極限學習機單次診斷圖 圖9 松鼠算法優化后極限學習機單次診斷圖 為了進一步驗證實驗準確性和魯棒性,對比了ELM、KELM、SSA-ELM三種方法重復20次實驗得到的訓練集和測試集的平均精度,具體數據見表3。 表3 實驗結果對比 % 由表3可知,SSA-ELM的平均訓練精度為100%,平均測試精度為98.18%,相比較于ELM和KELM具有更高的診斷精度。 本文對滾動軸承故障診斷方法進行了研究,通過ICEEMDAN和奇異值方法完成對軸承故障振動信號的特征提取,并將提取到的奇異值特征輸入到本文提出的SSA-ELM模型中,完成了對西儲大學軸承數據集的10類故障狀態的識別。結果證明,基于SSA-ELM的滾動軸承故障診斷模型準確率可達98.18%,相比于傳統的ELM、KELM模型而言,診斷準確率分別提高了7.76%和4.64%,該方法有較高的識別精準和識別能力。2.2 極限學習機
2.3 SSA-ELM模型
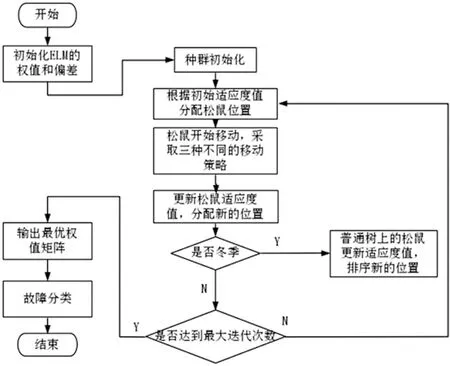
3 實驗分析
3.1 數據準備

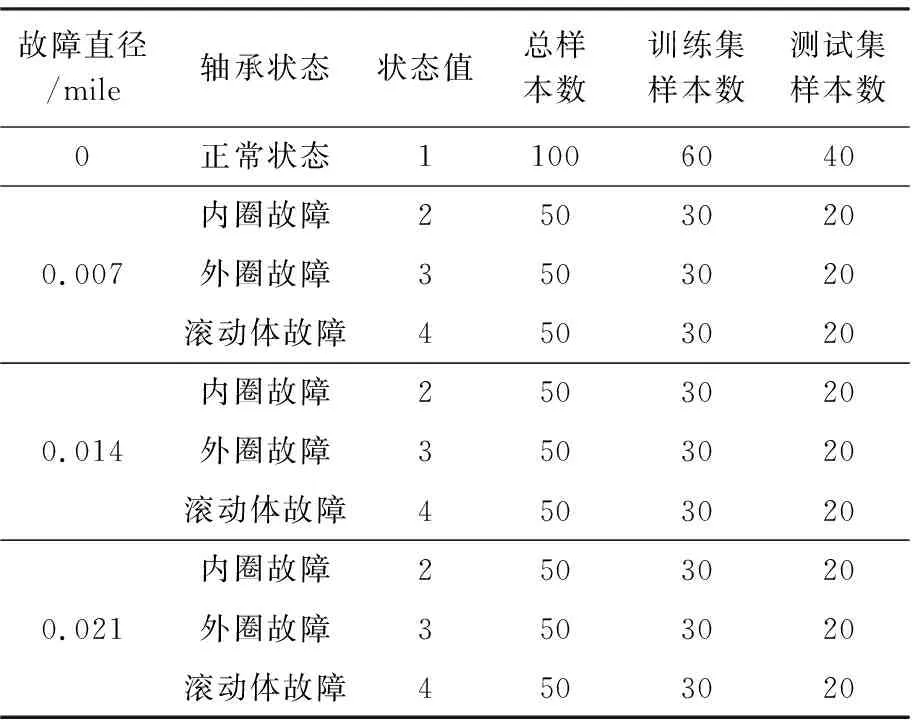
3.2 信號分析和特征提取
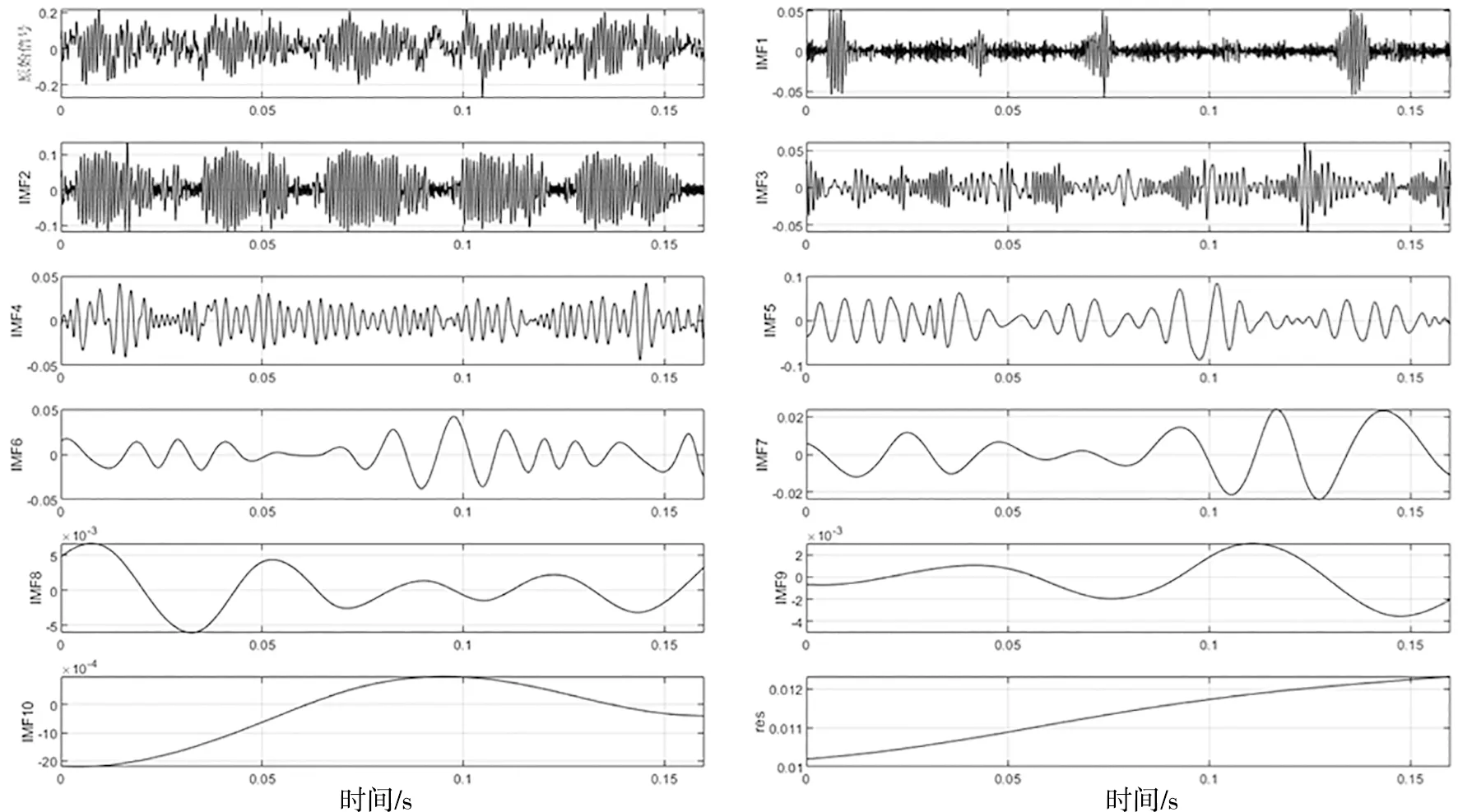
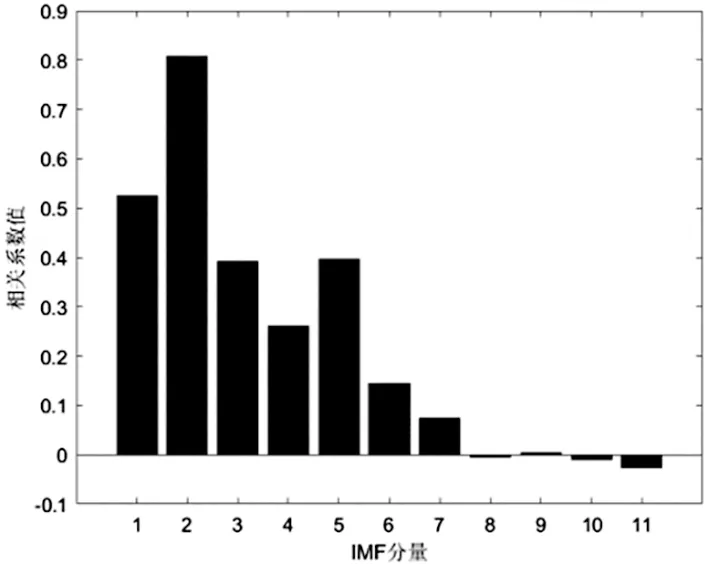
3.3 故障診斷

4 結 語

