重慶縉云山森林火災干擾邊坡的滑坡易發期預測

李 通，王云琦 ，祁子寒，何相昌，李克文

（1. 北京林業大學水土保持學院重慶三峽庫區森林生態系統教育部野外科學觀測研究站,100083,北京；2. 北京林業大學水土保持學院重慶縉云山三峽庫區森林生態系統國家定位觀測研究站,100083,北京）

0 引言

森林自然火災常由夏秋季節地表層干旱和積溫造成，過火林地受高溫灼燒影響，一方面地表失去植被屏障，土壤性質發生明顯變化，另一方面地下植物根系消亡，固土能力喪失，殘留根孔，火災跡地成為淺層滑坡和泥石流等次生災害的敏感區域。據統計火災跡地上泥石流和滑坡發生的概率高達40%[1-2]。火后森林根系固土護坡研究對火災跡地次生滑坡災害的預測對未來森林管護和防災具有重要意義。

關于森林火災后次生地質災害和土壤侵蝕的研究最早見于國外文獻統計，如1934 年的加州洛杉磯火后泥石流摧毀483 座房舍，30 人遇難[3]；2002 年科羅拉多州傳教士嶺的火災損毀 29 185 hm2森林，火后泥石流沖毀了橋梁公路及車輛[4]。國內對火災后淺層邊坡穩定的關注也在近十年內逐漸增多，最有名為2014 年甘孜仁額擁溝流域的森林火災及災后泥石流事件[4-6]和2020 年涼山森林火災及泥石流事件，兩例事件均造成了大量公共設施和生命財產損失。多項研究表明火災后的1～2 a 內易發生地表徑流型泥石流[1]，而在5～10 a 內則容易發生淺層滑坡[7]。前者常因過火林地表層滲透性降低甚至形成斥水層[8]，由邊坡表層超滲產流引起，而后者則多因為植被根系逐漸消亡和固土能力喪失而導致[9]。植物根系的固土強度是動態的，該動態變化引起的土體強度在坡體穩定性中發揮重要作用，根系除了因地上部分移除而腐爛造成活根數量變化外，也包括植物重植和生長造成的根系纖維自身強度的衰減-增強變化，因此根系對土體的凈增加強度，即根系固土能力在災害干擾后會發生衰減-回彈的現象，從而導致了一個滑坡易發期[10]。

當前數值模擬手段已成為分析植被邊坡防護效益的主流方法，MAO 等[11]通過“林島-黏聚力增量模型”模擬了三維邊坡形態，根層厚度，林島位置對穩定系數的影響，指出未來研究中對根系固土能力時間效應的迫切需求；李通等[12]通過有限元理論模擬了外力荷載下根土體的變形和整體穩定過程；稽曉雷等[13-15]通過強度折減法模擬了不同根系分布和生長期限對邊坡位移的限制作用。然而當前關于火災后植物根系死亡-再生過程中根系固土強度的時間動態研究成果極少，暫無可靠的土體強度動態量化方法，少有的研究案例[14-17]只提供了短期的測量數據案例，很難考慮災后長期根系強度全生命周期動態，這成為了火災跡地邊坡滑動易發期預測研究的最大障礙。SIDLE 等[18-19]對人工砍伐森林的根系進行了長期監測研究，發現森林砍伐后根系強度衰減和恢復的時間動態可分別描述為反曲函數和指數函數，并通過實際監測的曲線拐點值、最大最小強度值回歸了根系固土強度模型，該模型在后來的俄勒岡州艾里奧特公園森林兩次滑坡事件中得到驗證[10]。雖然人工砍伐和火災有著本質的區別，但同為土壤內部根系固土能力的衰減恢復問題，因此在長時間序列監測數據缺乏的情況下，LEE 等[20]對韓國首爾等地2002—2020 年森林火災后滑坡研究中發現SIDLE 曲線和滑坡頻率具有高度一致性，本研究將SIDLE 模型應用于本區未來淺層滑坡災害預測。

2022 年8 月21—26 日縉云山林火事件引起了社會廣泛關注，其中北碚區虎頭村上方的針闊混交林影響最為嚴重，林緣大面積灌草被毀。本研究對該區土壤根系做了實地調查和室內試驗，并采用數值模擬手段分析區域可能的滑坡成因，同時對已有文獻中各地區植物損毀后固土強度的恢復和衰減數據進行分析，采用SIDLE 根系動態固土強度預測模型對災后滑坡易發時間做保守估計，以期為災后森林養護和類似的次生災害防治提供參考。

1 理論和方法

1.1 根土試樣采集與力學試驗

選取重慶縉云山北碚區虎頭村上方的針闊混交林為研究采樣地（圖1 a），于嚴重過火范圍的下坡至坡腳處選取3 個采樣點，采樣點垂直坡向一字排列，間隔4 m。每采樣點移除倒木和表層灰燼，采用（圖1b）所示的汽油土鉆原地鉆孔（鉆頭裝載環刀直徑Φ=61.8 mm，高h=100 mm），鉆頭每入土20 cm 取出環刀，現場破碎并收集原狀土樣中的根系，用于根系量統計，收集鉆孔深度為40、140、230 cm 土層深度的原狀土柱，每土層至少3 個100 mm 土柱。同時，在取樣點附近對林緣優勢灌木大頭茶（Gordonia acuminata）和四川山礬（Symplocos setchuensis Brand）根系進行挖掘和采集帶回實驗室。室內先按照TST-55 變水頭試驗儀環刀的尺寸裁切為Φ=61.8 mm，h=50 mm 的試樣（每土柱可裁2 個試樣）進行滲透試驗，測定飽和滲透系數，然后將滲透完的飽和土樣按照Z-J四聯直剪儀環刀尺寸二次裁切為Φ=61.8 mm，h=20 mm的土餅（每試樣可裁2 個土餅），篩選無根系殘留的素土土餅（較細根系拔除）在0.8 mm/min 速率下進行快剪（圖1c）。篩選無損傷根樣，統一裁剪為100 mm，兩端采用樹脂處理[20]后進行單根抗拉測試（圖1d）并記錄斷口直徑。根系抗拉強度采用式（1）計算，并按照根系直徑和抗拉強度負冪函數曲線擬合：

圖1 火災林地調查及試驗Fig.1 Field survey and tests on burnt forestland

式中Tr為根系抗拉強度，MPa；F為根系抗拉力，N；d為根系直徑，mm；α和β為擬合參數。

1.2 火災后根系固土能力預測(SIDLE 曲線模型)

植物根系抗拉強度Tr在土體承受剪切時充分激活，產生抵抗剪切作用的效果，即根系固土能力，當前所采用的根系固土能力測試和量化方法多引自文獻[21-22]的系列成果，文獻[21]中WU 等計算模型為

式中ΔS為根系固土強度，kPa,As為根-土復合體剪切面面積，m2；k為模型中根系系數，取1.2[22]；n為根系徑級數；N為各個徑級根系數量；RAR為根系截面積比，1；為第i徑級根系的平均抗拉強度，MPa；N為 第i徑級根系的總數。根系直徑分級為：1～2、＞2～3、＞3～5、＞5～10 mm。

將根系固土強度量化為獨立于土體正應力的形式納入Mohr-Coulomb 框架[23]：

式中c′ 為有效黏聚力，kPa；φ′ 為有效內摩擦角，（°）；(ua-uw)為基質吸力，kPa；χ為基質吸力系數，以飽和度取值；σ為正壓力，kPa；ua為孔隙氣壓力，kPa；uw為孔隙水壓力，kPa。

火災發生后，一方面過火范圍內地被物被大量燒毀，殘留根系因腐爛而減少，強度逐漸喪失，另一方面，部分殘存樹木和次生灌木逐漸萌蘗，近表層根系強度又逐漸恢復。SIDLE 等[18-19]基于加利福尼亞州某針闊混交林砍伐25 a 后根系強度變化，并結合O’LOUGHLIN 等[24-26]的試驗數據，提出了根系恢復系數模型R和衰減系數模型D：

式中R和D分別為根系固土能力恢復系數和衰減系數，分別為根系生長和死亡條件下當前固土能力與最大固土能力的比值，無量綱；t為森林砍伐后的時間，a；d1、d2、d3、d4、d5和d6為擬合參數，通過監測的根系強度-時間數據擬合得到。

因此，森林砍伐后一段時間t的凈根系固土能力Δτ(t)，即SIDLE 模型計算式為

式中Δ τ(t)為砍伐時間t后的根增抗剪強度，kPa；Δcmax為最大抗剪強度，kPa；取值式（2）量化的ΔS。

當參數取值d1=-0.05，d2=0.95，d3=20.00，d4=0.25，d5=0.50，d6=0.75[10]時，復現文獻[10]中的SIDLE曲線如圖2。

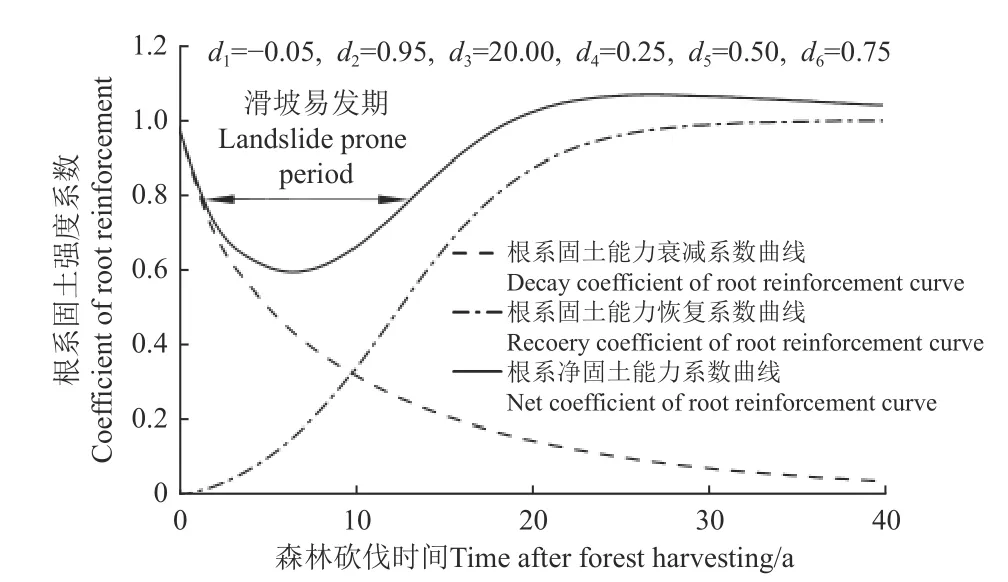
圖2 SIDLE 曲線模型-森林砍伐后根系固土強度Fig.2 The root reinforcement estimation model by SIDLE after forest harvesting

SIDLE 限定了R的變化區間為（0，1），建議R擬合的特征數據為曲線拐點（ti,Δτi）和2 倍時間拐點（2ti,Δτ），即R(t)的二階導在ti處為0，因此有以下條件：

以下將根據這3 個假定條件探討參數之間的關系，將式（5）代入式（8）有：

將式（11）進一步化簡：

同樣，將式（5）代入式（9）有：

式（13）進一步化簡：

至此，d2、d3、d4均可用d1來表示，可得僅包含ti和d1的R表達式：

按照以上參數關系，在區域長期連續性監測數據匱乏的情況下，結合文獻中已知的喬灌木數據可推算植物固土強度恢復的拐點時間分布，從而據拐點反推其他參數。SIDLE 曲線中“滑坡易發期”的確定依據為固土強度曲線谷值和實際災害在時間上的高度一致性，但并無具體強度或穩定系數的數值界定。本研究中將參考多個已知植物的拐點時間來確定快速恢復和慢速恢復2 種模式下的曲線谷值，并以2 個谷值間隔作為滑坡易發期來計算穩定性。

1.3 邊坡模型及數值模擬試驗

參考調查點邊坡和土壤條件構建幾何模型，坡度取30°，坡高取15 m，坡肩和坡腳延伸10 m 以減小邊界影響。邊界條件：力學方面，底部為全位移約束，四圍為法向位移約束，表面為自由面；滲流方面，上表面為降雨邊界，不考慮陡坡面積水，以降雨流量80 mm/d 輸入，持續4 d，模擬降雨小于土體入滲能力的完全入滲情景。前后兩面以水頭控制地下水位于0 m，模擬初始孔隙水壓力（pore water pressure,PWP）隨高程的線性分布；兩側面為對稱邊界，法向流量為0。為做位移數據分析，在邊坡中段1 m 深處設置監測點，坐標（14,5,7），詳見圖3。

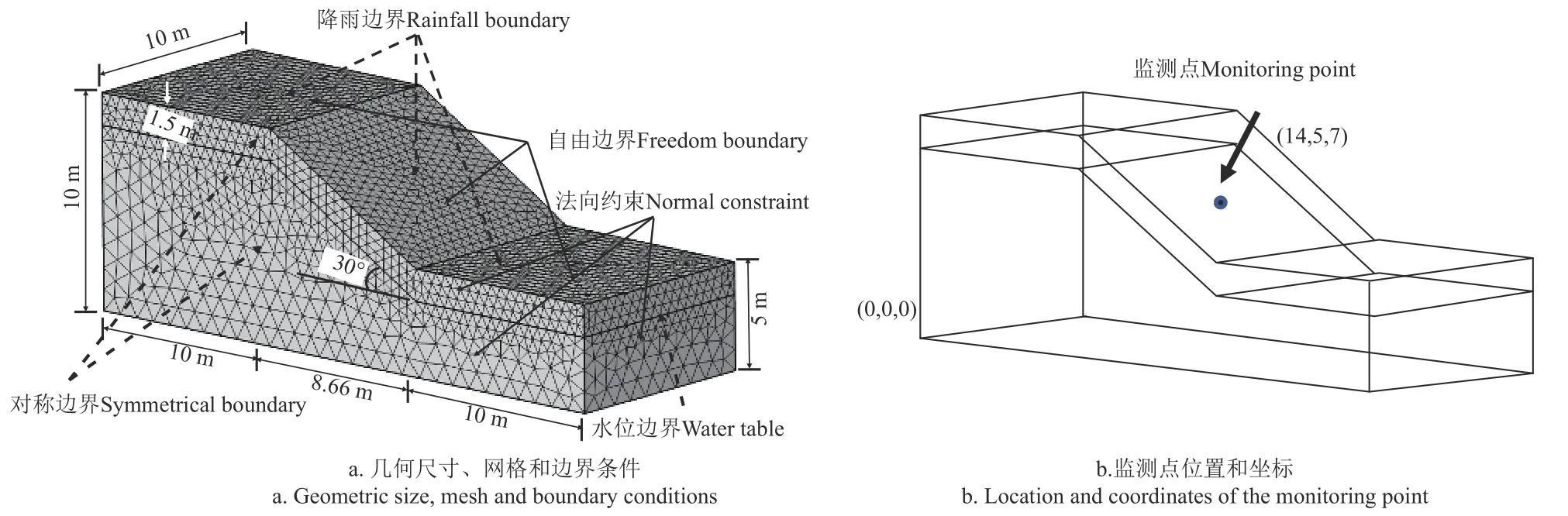
圖3 邊坡模型邊界條件及網格剖分示意Fig.3 Boundary conditions and mesh physics generalization of slope model

參考鉆孔的土層深度數據，將邊坡土體以1.5 m 深度分為0～1.5 m 和＞1.5 m 兩層，設定土體力學和滲透性參數，由于土體的彈性模量和泊松比僅會影響彈性位移，對穩定系數的影響極小，采用經驗賦值，含根土的泊松比和彈性模量分別略小于和大于無根土[27]，其他實測參數賦值見表1。考慮灌木林情境，個別粗壯根系的錨固效應較弱，根系固土能力統一概化至附加黏聚力，并考慮其在垂直方向的變異，某時間節點Δτ的賦值在軟件中以插值函數輸入，即Δτ=int(Z)，每隔1 a 賦值一次，重復計算至40 a。

表1 邊坡模型力學水力參數Table 1 Mechanical and hydraulic parameters of slope model

計算思路和物理場設置分3 步進行（圖4）：1）在滲流和力學邊界控制的初始條件下進行穩態分析，計算初始孔隙水壓力場和應力場，在彈性賦值和塑性賦值的條件下逐步消除應變和位移[28]；2）施加降雨邊界，進行降雨過程中孔隙水壓力瞬態變化條件下邊坡有效應力場和位移場的求解；3）對第2 步中各個時間節點進行強度折減[29]，計算邊坡整體穩定性。

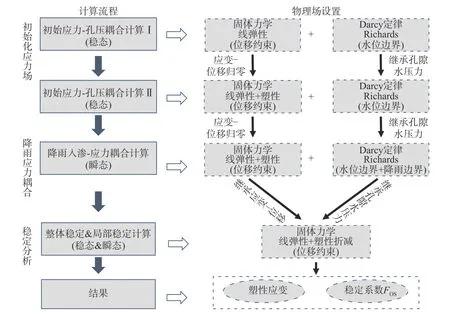
圖4 COMSOL 中的計算思路及模擬流程Fig.4 Calculation procedure and simulation step diagram in COMSOL

式中cm為臨界狀態黏聚力，kPa；φm為臨界狀態內摩擦角，（°）；FOS為折減系數，即邊坡的整體穩定系數。

降雨入滲時表層孔隙水壓力梯度較大，對上層土體加密處理，自上而下漸疏，最小尺寸0.005 m，最大尺寸1 m，共7 2 887 個單元（圖3），以保證收斂性和結果精度。其中經步驟1）導入步驟2）邊坡初始位移值7.37×10-5mm，遠在毫米級以下，說明用于正式分析的初始應力和初始孔隙水壓力在給定邊界下平衡效果良好，確保了模擬計算的可靠性。

2 結果與分析

2.1 SIDLE 模型曲線擬合參數分析及取值

林火畢竟為低概率事件，區域自1961—2021 年都無火災事件，期間也無根系的連續性監測數據，不可能實現模型6 個參數的嚴格擬合。對極少文獻資料中長時間序列數據進行了自定義非線性擬合，擬合效果見圖5～圖6。其中文獻[6]為四川涼山蘇格蘭松（Pinus sylvestris）固土強度衰減數據；文獻[18-19]及文獻[6]分別為SIDLE 對各地6 種植物和四川涼山蘇格蘭松的固土強度衰減數據；文獻[30]為原作者模擬的9 種喬灌木固土強度增長數據，本研究將其換算為0～1 之間的R值。

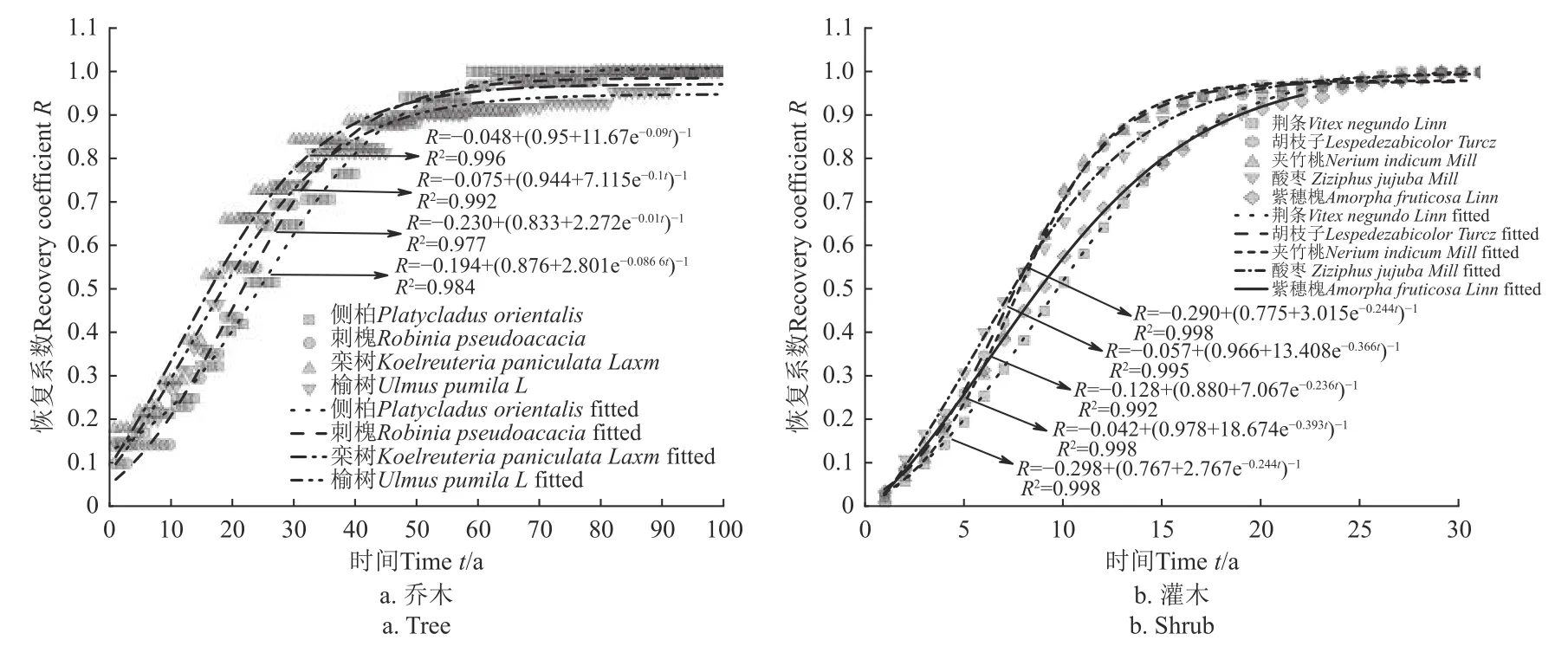
圖5 9 種植物根系固土能力恢復系數擬合曲線Fig.5 Fitted root reinforcement recovery coefficient curves of 9 plant species

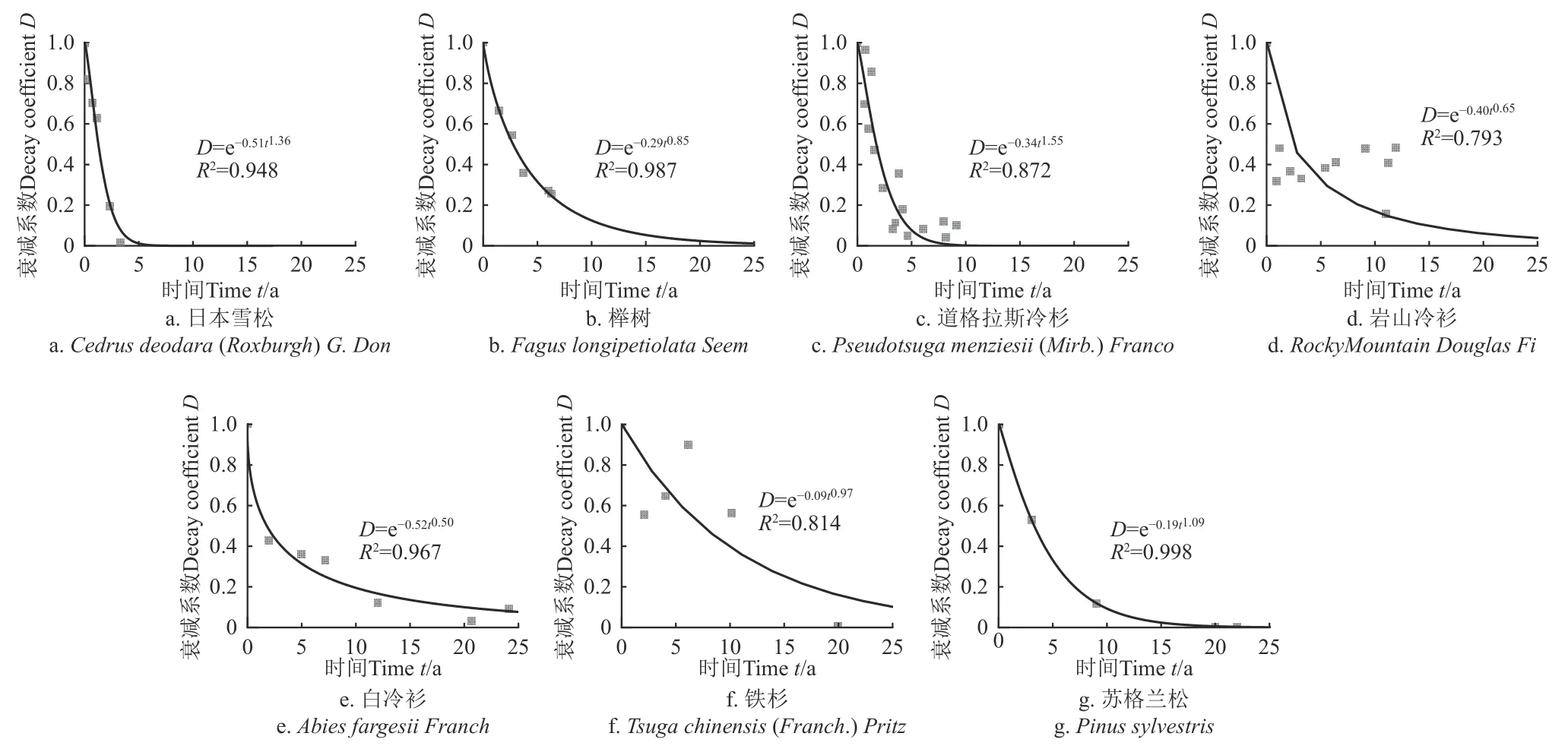
圖6 7 種植物根系固土能力衰減系數擬合曲線Fig.6 Fitted root reinforcement decay coefficient curves of 7 plant species

由圖5 可知，9 種喬、灌植物的擬合參數差別較大，R2均在0.97 以上，SIDLE 提出的R曲線模型可較好地反映樹木移除后的根系固土強度動態，但拐點時間ti不易從圖中直接分辨。圖6 中SIDLE 統計的根系強度衰減曲線主要為針葉樹種，衰減速率差別較大，完全消亡的時間在5～25 a 不等，其中四川涼山研究的蘇格蘭松（圖6f），研究地距本區僅700 km，同屬亞爾熱帶季風氣候，本區域森林生境最為接近，因此本研究直接采用了其衰減曲線參數d5=-0.19，d6=1.09。基于圖5 中的擬合參數，通過式（15）得到這些植物固土能力恢復的理論拐點時間ti，其分布見圖7，可知灌木樹種的恢復時間拐點較喬木更靠前，超過該時間后進入快速恢復階段。考慮本研究植物對象為灌木根系，僅以5 種灌木（圖7a）的拐點時間ti范圍（4.9～9.7 a）和恢復系數R范圍（0.51～0.62）為參考，來確定一般灌木的恢復模式，并應用到本地區。分別取“最長拐點時間+最小恢復系數組合（ti=9.7 a，R=0.51）”和“最短拐點時間+最大恢復系數組合（ti=4.9 a，R=0.62）”作為慢速恢復和快速恢復模式，從而計算其他參數（式（12）～（15））。由此確定本研究區域的SIDLE 曲線及參數見圖7b。

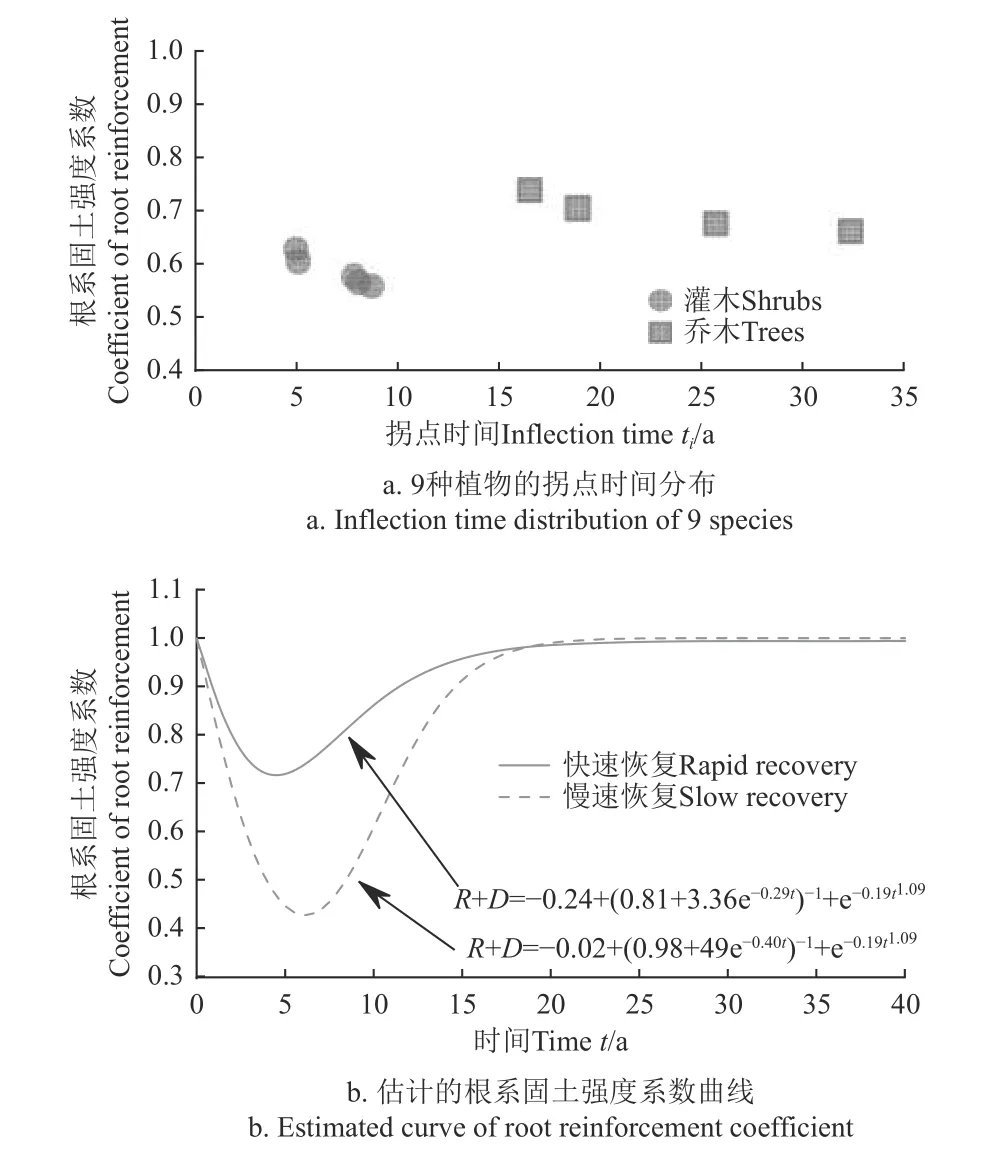
圖7 由時間拐點估計的根系固土強度曲線Fig.7 Estimated root reinforcement curve according to inflection time points

2.2 林地土體抗剪和滲透特性

圖8 中為3 個鉆孔至少4 個成功滲透試樣的飽和滲透系數（圖8a）和抗剪強度參數（圖8b）的均值和極值，可知土體滲透系數Ks隨深度增大呈降低趨勢，表層相對松散的土體測試偏差明顯高于深層緊密結構的土體，并且在1.4 m 以下有明顯的數據降低，上下層的均值分別5.2×10-6和1.5×10-6m/s，相差3.47 倍。與飽和滲透系數分布相似，表層松散土體具有較大的黏聚力，深層緊密土體具有較大的內摩擦角和較小黏聚力。黏聚力和內摩擦角也在1.4 m 附近存在數據突變，以約1.4 m 為分界，上下層土體黏聚力總均值分別為5.5 和1.8 kPa，上下層內摩擦角總均值分別為 18°和26 °，上下層黏聚力和摩擦角的總均值相差分別達到3.06 倍和0.69 倍。

圖8 土壤剖面上飽和滲透系數和抗剪強度指標隨深度變化Fig.8 Change of saturated conductivity and shear strength parameters with soil depth

2.3 林地根系分布特征與固土強度

圖9 為研究點采集單根抗拉強度隨直徑變化曲線，可知2 種優勢植物根系的抗拉強度均隨直徑呈負相關關系，細根抗拉強度明顯高于粗根，大頭茶和山礬的擬合方程分別為Tr=25.65d-0.47（R2=0.712）和Tr=29.18d-0.53，（R2=0.638）。2 種植物總體強度-直徑曲線相差不大，考慮2 種植物在土壤中的生長交叉，采樣時顏色均為灰褐色不易區分，為方便進一步的固土能力估計，將2 種植物的數據混合后擬合如實線所示，擬合參數為Tr=26.12d-0.49（R2=0.699）。

圖9 根系抗拉強度和直徑擬合曲線Fig.9 The fitted curves of root tensile strength versus diameters

鉆孔環刀內的根系數量隨土層深度分布（每個深度5 環刀根系數量總和）如圖10a 所示，根系數量整體上隨土層深度增大而減小，在第2 層具有最大根系數量，1 mm 細根系主要分布與0～0.4 m 土層，＞5～10 mm 較粗根系分布于0.4 m，0.8 m 深度以下幾乎未統計到根系，說明調查點的灌木扎根較淺。結合圖9 根系強度參數，采用式(2)對土層的根系固土能力計算結果進整理如圖10b，可知根系對土體強度的貢獻主要在表層砂質壤土層1 m深度范圍，與根系數量分布趨勢接近，根系截面積比與附加黏聚力基本表現出正相關的特點，說明根系固土能力由含根量主導，根系固土能力在0.4 m 為最大，可達到18 kPa，1 m 以下根系對土體強度無貢獻。

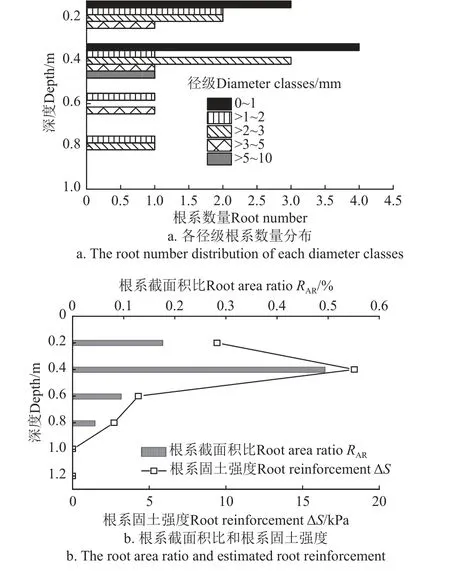
圖10 土壤剖面上根系數量、截面積比和根系固土能力Fig.10 The root number,root area ratio and root reinforcement along soil profile

2.4 降雨過程中邊坡滲流與變形過程

圖11 為降雨1～4 d 過程中邊坡滲流場變化，可知滲流場的變化分為3 個階段：1）表層土體濕潤，隨深度線性分布的初始PWP 在邊坡表層有明顯升高，濕潤鋒快速向下推移，深層土PWP 尚無變化（圖11a～11b）；2）濕潤鋒到達土層結構面，雨水聚集形成局部飽和帶(白色0 kPa 等值線)，并伴隨著順坡滲流現象（圖11c）；3）飽和帶水位線逐漸升高向上坡位蔓延，整個結構面出現正PWP（圖11d）)，最大約10 kPa，坡腳積水逐漸透過結構面向下層土體滲流，但地下水位仍無升高現象。

圖11 降雨過程4 個時間節點邊坡孔隙水壓力變化云圖Fig.11 Temporal pore water pressure (PWP) field of slope at 4 time-nodes during precipitation

圖12 為降雨1.0～4.0 d 過程中邊坡位移場云圖及位移矢量標注，降雨初期，最大位移出現在初始基質吸力最高的坡肩處(圖12a)，表現為輕微膨脹，隨著降雨進行，最大位移帶逐漸向下坡位置移動(圖12b)，當結構面出現積水后，下坡位的水平位移分量迅速增大(圖12c)，邊坡逐漸呈現出沿結構面的平直型滑動 (圖12d)。圖13 為對1.0～4.0 d 的4 個時間節點的強度折減結果，計算暫不考慮根系固土作用，降雨初期，邊坡具有較高的穩定系數FOS=1.91，塑性貫通帶位于邊坡深層3.9 m，呈現圓弧狀（圖13a），隨著降雨持續，深層的塑性貫通帶逐漸變淺（圖13b），FOS也逐漸降低1.72，當結構面出現積水后，塑性貫通帶開始轉移到結構面處（圖13c～13d），FOS迅速降低至1.13，瀕臨失穩（圖13d），說明邊坡深層土體強度具有較高的安全儲備，而表層土體受降雨影響，有效應力降低幅度遠大于深層，最初的深層弱滑動趨勢轉化為淺表層的強滑動趨勢。考慮根系固土作用時，邊坡特征點位移及FOS與裸坡對比如圖14，由圖14a 可知坡體中下部位在降雨前期僅發生較小位移，結合圖12 可知該位移為表層土體濕潤后基質吸力快速降低發生輕微膨脹（0.25 mm），由于土壤容重增大該變形在數小時內恢復為0，在18 h 開始產生階躍狀蠕動變形，至3.5 d 積水帶逐漸形成，出現正PWP，進入淺層土體的加速形階段。有根系加固的植被邊坡和無根裸坡在降雨前期位移接近，進入加速階段后，根系對位移的限制作用逐漸凸顯，與裸坡相比在降雨末期根系對總位移的減小達到30%。圖14b為植被邊坡和裸坡的FOS對比，二者具有相同的時程變化，均在約3.0 d后開始驟降，整個降雨過程中根系對FOS的貢獻率由最初6.8%變化至19.8%。

圖12 降雨過程中4 個時間節點邊坡總位移變化Fig.12 The temporal development of total displacement at 4 time-nodes during precipitation

圖13 降雨過程中4 個時間節點邊坡折減的等效塑性應變發展Fig.13 The temporal development of equivalent plastic strain at 4 time-nodes during precipitation by strength reduction

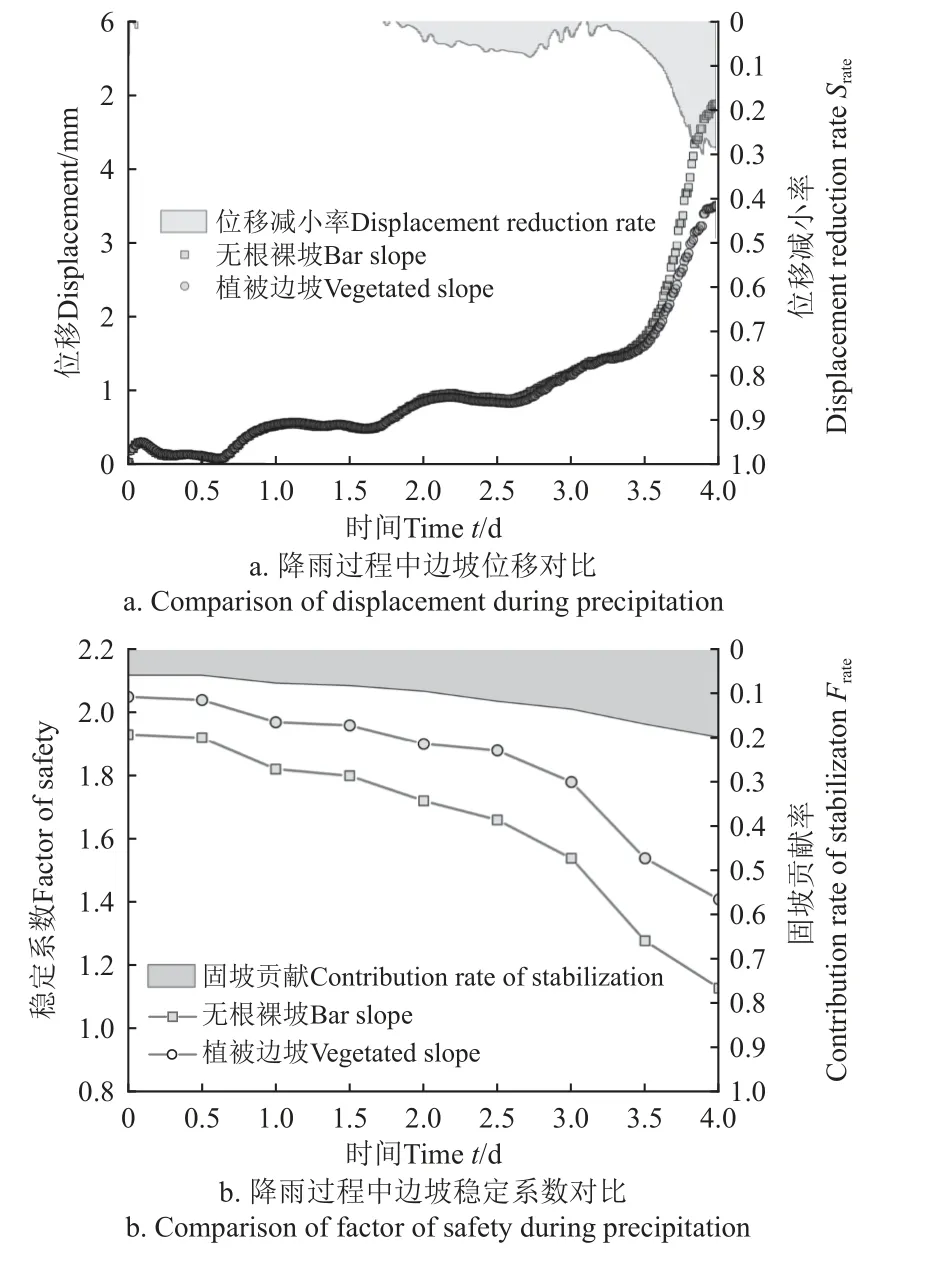
圖14 降雨過程中植被邊坡與無根裸坡的位移和穩定系數對比Fig.14 Comparison of total displacement and FOS between vegetated slope and bar slope during precipitation

2.5 森林火災后滑坡易發期和恢復預測

火災后40 a 內自然狀態和極端降雨狀態下邊坡的穩定性結果如圖15 所示，快速恢復和慢速恢復模式對應的穩定性谷值分別為9 和6 a，火災后邊坡在自然狀態下Fos變化不大，6～9 a 分別從初始2.05 降低至1.9 和2.0，降低幅度分別為7.3%和2.4%，依然處于穩定水平。這是因為森林土體在較干燥狀態下潛在破壞層位于遠離植被發育層以下的深處（圖13a），表層根系的存在與否，僅影響坡腳剪出口和坡頂剪入口局部強度，不會對深層造成較大影響；而在極端降雨后，邊坡潛在滑動面位于淺層（圖13c～13d），快速和慢速恢復模式下FOS隨災后年限迅速降低，在第6～9 a 從火災前的1.41 降低至1.32～1.22，降低幅度分別為6.40%和13.48%，此為滑坡易發期，隨后隨著根系繼續恢復，邊坡穩定性逐漸提高，至18～24 a 恢復到火災前的水平。即使在慢速恢復模式下，火災后第9 a 邊坡遭遇極端降雨下FOS為1.22，依然大于裸坡狀態（FOS=1.13）（圖13d、圖14b），根系發揮了關鍵的強度補償作用。

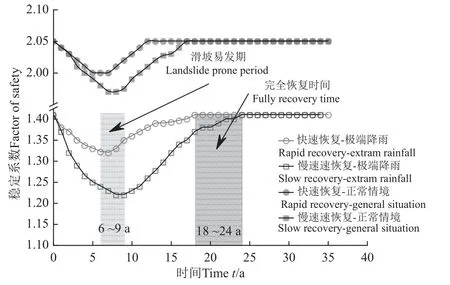
圖15 火災后邊坡穩定性預測Fig.15 Slope stability prediction after forest fire

3 討論

本研究對縉云山過火林地的土壤及根系現狀進行了初步調查和室內試驗，基于流固耦合理論建立了數值模型，采用SIDLE 曲線對森林火災后40 a 內邊坡在自然狀態和極端降雨后穩定性動態做了評估。自然狀態下，邊坡處于較穩定狀態，潛在滑動層位于深層的砂質泥巖層，這得益于下層土體較高的摩擦角和較低的滲透系數；極端降雨入滲使表層砂質壤土層基質吸力喪失，在砂質壤土和泥巖層交界面上形成暫態飽和帶[31-32]，與前人的雙層土坡結構模擬結果類似。所得降雨中位移的發展符合滑坡演變規律[33]。本研究明確了類似本區域地質條件的邊坡失穩機制為：土層結構面上基質吸力轉化為正孔隙水壓力從而降低了土體的有效應力，這不同于深厚黃土基質吸力降低或者濱水岸坡的坡腳水位升高導致的邊坡失穩。

降雨中FOS先緩慢降低后快速降低的結果揭示了植被邊坡最危險滑動面由深層向淺層演變的失效過程。黃月華等[34]研究也發現降雨中植被覆蓋邊坡的FOS隨時間變化存在臨界時間，超過該時間后FOS開始驟降，且該臨界時間與上覆層滲透性和順層滲流現象密切相關，佐證了本研究所揭示的縉云山滑坡形成機制。

火災干擾對土體和根系性質的影響機制復雜，力學方面，除了土體滲透性和抗剪強度的降低外，還有根系自身強度的衰減[16-19]，考慮這些效應在短期的根系更新和土體沉降后得到恢復[17]，因此在在長期預測問題中僅考慮根系數量變化，圖10b 的結果也反映了根系固土能力主要取決于根系數量；水文方面，有研究者強調了植物消亡后因蒸散發減少而導致的基質吸力喪失、根系死亡腐爛造成的優先滲流路徑等水文效應對土坡穩定產生不利影響[35-37]，本研究中未考慮該效應可能低估滲流飽和的時間，因此所估計的單場降雨失穩時間節點4 d 略遲于實際，而臨界狀態結構面上的有效應力主要受控土體飽和后的孔隙水壓力大小，因此所計算的FOS大小不受該效應影響。

對火災后數十年內的穩定性變化的模擬依賴于精準的根系監測數據，國內對火災和邊坡穩定的專項研究極少，如雷鳴宇等[6]通過連續調查數據，采用無限斜坡模型分析了四川省涼山州木里縣的火后9 a 內的淺層滑坡穩定性動態，并給出了根系數量和穩定性單調遞減的指數型預測函數，預測的滑坡期約為火后8 a；LEE 等[20]近期研究中也發現韓國首爾等地的森林火災后滑坡在6～10 a 頻率最高，且恢復期大于20 a，本研究的預測結果與之接近。與文獻[10]的研究相比，SIDLE 模型考慮了根系恢復過程，更嚴謹。有限元流固耦合的方法較無限斜坡模型也具有進步性，所模擬的火后穩定性動態反映了植被死亡-恢復過程中FOS快速降低后緩慢恢復的趨勢。縉云山1989 年6 月有特大風災歷史，當時包括本研究點在內的60 hm2林木連根毀壞，11 a 后形成垂直分化結構，16 a 后演替為如今的常綠闊葉林-灌木林結構[38]。這與本研究估計的18～24 a 完全恢復邊坡穩定較接近，說明采用多植物恢復拐點時間估計的SIDLE 模型參數基本可信。

該研究僅分析了30°邊坡情境，顯然區域內更陡邊坡或土體結構強度更差的邊坡未來則面臨更大的滑坡風險。本例為對未然事件的理論預測，無論是上文中SIDLE 曲線參數的取值策略、或是SIDLE 的曲線參數取值[17]，還是LEE 等[20]基于歷史數據對SIDLE 曲線的驗證研究，都存在多植物數據混合借鑒的情況，這是監測數據匱乏條件下迫切應用和科學嚴謹性的權衡和妥協，可見，未來在森林生態研究中還應加強對地下植物根系連續監測和調查工作。本研究所給出的結果可為近期火后森林邊坡防護提供初步借鑒，有待未來數十年連續調查研究的檢驗。

4 結論

1）縉云山林緣邊坡為約1.5 m 厚的砂質壤土-砂質泥巖雙層土坡結構，上下層滲透性差異懸殊，上層飽和滲透系數為5.2×10-6m/s，是下層的3.47 倍，上層黏聚力均值為5 kPa，摩擦角為18°，分別為下層的3.06 和0.69 倍。

2）區域的林緣邊坡在正常情況下處于穩定狀態，潛在滑動面位于深層（穩定系數FOS＞2）,極端降雨（80 mm/d×4 d）后，在土層結構面上容易出現帶狀積水帶，積水孔隙水壓力約10 kPa，局部的正孔隙水壓力減小了有效應力導致淺層滑動。極端降雨后裸坡臨界穩定系數FOS為1.13，考慮當前根系固土的穩定系數FOS為1.41，當前根系護坡貢獻為19.8%。

3）火災發生后數年內，根系消亡對正常情況下深層邊坡穩定性無明顯影響，而極端降雨后淺層邊坡穩定性隨火災后的年動態呈現快速降低后緩慢恢復的曲線趨勢，估計在火災后6～9 a 間出現滑坡易發期，在火災后18～24 a 才可完全恢復火災前的穩定狀態，該結果可作為火災后治理參考。