與J1有相同元素最高階和次高階及Sylow 2子群的階的有限群①

陳婉平， 陳貴云

西南大學 數學與統計學院，重慶 400715

在有限群的研究中, 群的結構往往可以通過一些數量關系刻畫出來, 例如: 著名的Lagrange定理、Sylow定理、Burnsidepaqb定理等.這些定理體現了群的數量刻畫的重要性, 而如何用更少的數量關系去刻畫群的更多性質是群論學者一直思考的問題.20世紀80年代初, 施武杰教授提出可以只用群階和元素階之集對有限單群進行刻畫的猜想.該猜想提出后, 眾多學者對此做了大量的研究, 最終在2009年得到完全證明, 即: 所有有限非交換單群都可以通過群階和元素階之集唯一確定.此后, 群論學者開始思考如何弱化該猜想的條件繼續研究單群的結構.例如: 文獻[1-3]只用群階和最高階元的階刻畫了散在單群、部分交錯群、部分對稱群; 文獻[4-5]去掉了群階這一重要條件, 只用最高階元的階和最高階元的個數及最高階元中心化子的階刻畫了Mathieu群、Janko群、部分交錯群; 文獻[6-9]討論了與交錯群或Mathieu群有相同元素的最高階和次高階及Sylow 2-子群的階的有限群的結構.當然僅用這3個數量條件并不能把單群唯一確定下來, 但是可以得這類群比較具體的結構, 所以本文將繼續此研究, 討論與J1有相同元素的最高階和次高階及Sylow 2-子群的階的有限群, 并得到了此類群的結構.本文所涉及的群都是有限群.設G為有限群,Γ(G)表示G的素圖,K1(G)表示群G的最高階元的階,K2(G)表示群G的次高階元的階,Gp表示群G的Sylowp-子群,|G|p表示群G的Sylowp-子群的階, 其他符號都是標準的.

引理1[10]有限群G的素圖不連通, 則下列結論之一成立:

(i)G為Frobenius群;

(ii)G為2-Frobenius群;

(iii)G有正規列1?_H?_K?_G, 使得H和G/K是π1-群,K/H是非Abel單群,H是冪零群, 其中2∈π1, 且|G/K|||Out(K/H)|.

引理2[11]設有限群G=KH是以K為核、H為補的Frobenius群, 則K是冪零群,H的Sylow子群是循環群或廣義四元數群,t(G)=2, 且Γ(G)的連通分支為π(H),π(K),|H||(|K|-1).

引理3[12]設有限群G是2-Frobenius群, 則G=ABC, 其中A?_G,AB?_G,B,C為循環群,AB是以A為核、B為補的Frobenius群,BC是以B為核、C為補的Frobenius群,Γ(G)恰有兩個連通分支, 且π1(G)=π(A)∪π(C),π2(G)=π(B).

引理4[8]設有限群G有2階無不動點自同構σ, 則G為Abel群, 且σ(g)=g-1(?g∈G).

Janko群J1的階為23·3·5·7·11·19, 元素的最高階為19, 次高階為15.本文我們證明如下結論:

定理1設有限群G的Sylow 2-子群的階是23,K1(G)=19,K2(G)=15, 則G同構于下列群之一:

(i)G=KH是以K為Frobenius核的Frobenius群,|G|=23·3a·5·7c·19f, 其中a=1,2,c=0,1,f≥1,K為初等Abel 19-群,H2為8階循環群或四元數群,H3,H5,H7為循環群;

(ii)G/H?J1,|G|=23·3a·5b·7c·11d·19f, 其中a,b,c,d,f≥1,H為p-群(p=3,5,7)或冪零{3, 5}-群, 且Exp(H)=p,9,15.

證由K1(G)=19,K2(G)=15, 及|G|2=23可設

|G|=23·3a·5b·7c·11d·13e·19fa,b,f≥1;c,d,e≥0

且易知19是Γ(G)的孤立點, 因此G的素圖不連通.由引理1, 我們按如下3種情形進行討論:

情形1 若G為Frobenius群, 由引理2可設G=KH, 其中

{2, 3, 5}?π(H)?{2, 3, 5, 7, 11, 13}π(K)={19}

若H?_G, 考慮K在H2上的作用知K必然平凡作用在H2上, 得G有38階元, 矛盾.因此K?_G為Frobenius核,H為Frobenius補.進而H中的2階元可以共軛作用于K, 且該作用是無不動點的.從而由引理4知K為Abel群, 故K為初等Abel 19-群.再由K1(G)=19, 及π(H)是Γ(G)的一個連通分支知(|H|, 11·13)=1, 即π(H)={2, 3, 5},{2, 3, 5, 7}.

若π(H)={2, 3, 5}, 由于H的Sylow子群只能是循環群或廣義四元數群, 從而H2為8階循環群或四元數群,H3,H5都是循環群, 又因K1(G)=19,K2(G)=15, 所以1≤a≤2,b=1.

若π(H)={2, 3, 5, 7}, 同理可得H2為循環群或四元數群,H3,H5,H7為循環群, 且1≤a≤2,b=1,c=1, 結論(i)成立.

情形2 若G為2-Frobenius群, 則由引理3知G=ABC, 其中

{2, 3, 5}?π(A)?π(C)?{2, 3, 5, 7, 11, 13}π(B)={19}

由于B為Frobenius群AB的補, 因此B的Sylow 19-子群為循環群, 從而|B|=19.再由BC是以B為核、C為補的Frobenius群, 故|C||(|B|-1), 即|C||18, 從而|A|2=4,8, 所以B在A2上的作用平凡, 導致G有38階元, 矛盾.因此G不是2-Frobenius群.

情形3 設G有正規列1?_H?_K?_G, 使得H和G/K是π1-群,K/H是非Abel單群,H是冪零群, 其中2∈π1, 且|G/K|||Out(K/H)|.下面根據d,e的取值分為4種情形進行討論:

情形3.1 設d,e≥1.此時

|G|=23·3a·5b·7c·11d·13e·19fa,b,d,e,f≥1;c≥0

情形3.2 設d≥1,e=0.此時

|G|=23·3a·5b·7c·11d·19fa,b,d,f≥1;c≥0

同情形3.1可知11,19為Γ(K/H)的孤立點, 因此t(K/H)≥3.分t(K/H)>3和t(K/H)=3兩種情形討論:

當t(K/H)>3時, 由文獻[13]和|K/H|2≤|G|2=23知K/H只可能同構于J1, 即

K/H?J1(23·3·5·7·11·19)

由|Out(J1)|=1可知|G/K|=1, 故G/H?J1, 此時|H|=3a-1·5b-1·7c-1.因為K1(G)=19,K2(G)=15, 所以H為p-群或冪零{3, 5}-群, 且滿足結論(ii)之條件.

當t(K/H)=3時, 由文獻[13]中給出的單群階分量表得K/H可能同構于下列群之一:

Ap,A1(q),2Dp(3)(p=2m+1),G2(q),2G2(q),2Dp+1(2)(p=2m-1),F4(q),2F4(q).

若K/H?Ap, 由于p,p-2為奇階分量且為素數, 因此p=19,p-2=11, 顯然不存在這樣的p, 故K/HAp.

若K/H?A1(q), 對q分3種情況討論:

(a)當2|q時, 設q=2m(m∈N+), 由K/H有3個階分量q,q+1,q-1可知q+1=11d,19f, 進而

q=11d-1=10(11d-1+11d-2+·s+1)

或

q=19f-1=18(19f-1+19f-2+·s+1)

與q=2m矛盾.

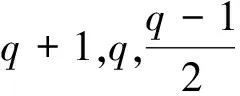
或

即5|19f或9|11d, 矛盾.

11d+1=(11+1)((-1)d-111d-1+·s-11+1)

故6|19f, 矛盾.因此2|d.于是令d=2t, 此時

q-1=11d-1=(11t-1)(11t+1)

如果2?t, 則由

q+1=11d+1=112t+1

知

矛盾.故2|t, 令t=2r, 即d=4r, 此時

q-1=11d-1=(11r-1)(11r+1)(112r+1)

如果2?r, 則

矛盾.故2|r, 令r=2k, 即d=8k, 此時

q-1=11d-1=(11k-1)(11k+1)(112k+1)(114k+1)

如果2?k, 則

矛盾.故2|k, 令k=2s, 則

d=16s

q-1=11d-1=(11s-1)(11s+1)(112s+1)(114s+1)(118s+1)

由于11s-1,11s+1,112s+1,114s+1,118s+1中任意兩個數的最大公約數為2, 因此q-1至少含有5個不同的素因子, 這與π(q-1)?{2, 3, 5, 7}矛盾.若q=19f, 同理可推出矛盾.因此K/HA1(q).

若K/H?G2(q)(q=3m,m∈N+), 由于K/H有3個階分量:q6(q2-1)2,q2+q+1,q2-q+1, 此時q6(q2-1)2=36m(3m+1)2(3m-1)2, 因此

24|36m(3m+1)2(3m-1)2=q6(q2-1)2

與|K/H|2≤|G|2=23矛盾.

32m+1+1=(3+1)(32m-32m-1+…-3+1)=4(32m-32m-1+…-3+1)

且

32m+1-1=(3-1)(32m+32m-1+…+3+1)=2(32m+32m-1+…+3+1)

于是

q3(q2-1)=8·36m+3(32m-32m-1+…-3+1)(32m+32m-1+…+3+1)

而32m-32m-1+…-3+1與32m+32m-1+…+3+1互素, 因此q3(q2-1)至少含有4個不同的素因子.又因π(q3(q2-1))?{2, 3, 5, 7}, 故π(q3(q2-1))={2, 3, 5, 7}.因為

32m+1±1=3·32m±1≡3(-1)m±1(mod 5)

即當m為奇數時, 32m+1±1≡-3±1(mod 5); 當m為偶數時, 32m+1±1≡3±1(mod 5).所以5?(32m+1±1), 進而5?q3(q2-1), 與π(q3(q2-1))={2, 3, 5, 7}矛盾.

若K/H?2Dp+1(2), 由p=2m-1(m≥2,m∈N+)知p>2, 則K/H的第一個階分量中2p(p+1)>26, 矛盾于|K/H|2≤|G|2=23.

若K/H?F4(q), 由q=2m(m∈N+)知K/H的第一個階分量中q24=224m≥224, 矛盾于|K/H|2≤|G|2=23.

若K/H?2F4(q), 由q=22m+1(m∈N+)知K/H的第一個階分量中q12=224m+12≥212, 矛盾于|K/H|2≤|G|2=23.

情形3.3 設e≥1,d=0.此時

|G|=23·3a·5b·7c·13e·19fa,b,e,f≥1;c≥0

由K1(G)=19可知13,19是Γ(G)的孤立點, 因此13,19也是Γ(K/H)的孤立點, 故t(K/H)≥3.與情形3.2一樣, 分t(K/H)>3和t(K/H)=3兩種情形進行討論, 同理可證這樣的單群K/H是不存在的.

情形3.4 設d,e=0.此時

|G|=23·3a·5b·7c·19fa,b,f≥1;c≥0

且19是Γ(G)的孤立點, 故19∈π(K/H)?{2, 3, 5, 7, 19}, 則K/H可能是單K3-群、單K4-群、2a13a25a37a419a5單群(ai∈N,i=1,2,…,5).而由文獻[14]知單K3-群的階不含素因子19, 因此K/H不是單K3-群.

若K/H是單K4-群, 則由文獻[15]知K/H可能同構于下列群之一:

L2(19)(25·32·5·19),L3(7)(25·33·73·19),U3(23)(29·34·7·19).

若K/H是2a13a25a37a419a5單群, 則由文獻[16]知K/H可能同構于下列群之一:

A3(7)(29·34·52·76·19),2A2(19)(25·32·52·73·193).

但是這些群的Sylow 2-子群的階都大于23, 與|K/H|2≤23矛盾.所以此類群不存在.