同階子群個數之集為{1, 3, p+1}的有限群①
龍雯, 晏燕雄
西南大學 數學與統計學院,重慶400715
本文所涉及的群都是有限群.設G是有限群,n(G)表示同階子群個數組成的集合,π(G)為|G|的素因子的集合,np為G的Sylowp-子群的個數, 其中p∈π(G).眾所周知, 有限群的數量性質與群結構的關系一直是群論研究領域的熱點, 許多群論學者從事過相關研究并取得了較好的研究成果.例如, 文獻[1]得到了同階子群個數小于或等于3的有限群的結構, 并證明了不存在同階子群個數之集為{1, 2}的有限群; 文獻[2]給出了同階交換子群個數之集為{1, 3}的有限群的結構; 文獻[3-4]研究了同階子群個數之集恰好包含2個元素的情形; 文獻[5]討論了n(G)={1, 3, 4}的有限群G的結構.對于任意給定的n(G), 目前尚未有一般性方法對群G給出完整刻畫.本文繼續該問題的研究, 并研究同階子群個數之集包含3個元素的情形, 主要結論如下:

(i)G的Sylowqi-子群Qi循環且Qi?_G,i= 1,2,…,n;
(ii)當P循環時,np=p+1;
(iii)當P不循環時,P?_G且P同構于Cpβ-1×Cp(β≥2)或〈a,b|apβ-1=bp= 1,b-1ab=a1+pβ-2〉(β≥3);
(iv)當P2循環時,n2= 3;
(v)當P2不循環時,P2?_G且P2同構于下述群之一:C2α-1×C2(α≥2), 〈a,b|a2α-1=b2= 1,b-1ab=a1+2α-2〉(α≥4),Q8.
為證明定理1, 需用到如下引理:
引理1[6]設G是p-群且|G|=pn,Sk(G)是G的pk階子群的個數(0≤k≤n), 則Sk(G)≡1(modp).
引理2[7]設G是p-群, 則:
(i)G/Φ(G)是初等交換群;
(ii)如果|G/Φ(G)|=pn, 則存在x1,x2,…,xn∈G, 使得G=〈x1,x2,…,xn〉.
引理3[8]設G是p-群且n(G)={1,p+1}, 則G同構于下述群之一:
(i)Q8;
(ii)Cpn-1×Cp, 其中n≥2;
(iii)〈a,b|apn-1=bp= 1,b-1ab=a1+pn-2〉, 其中p≠2,n≥3;
(iv)〈a,b|a2n-1=b2= 1,b-1ab=a1+2n-2〉, 其中n≥4.
定理1的證明
令P2∈Syl2(G),P∈Sylp(G), 以下將分4種情形給出證明:

步驟1.1G的Sylowqi-子群Qi循環且Qi?_G, 其中qi≠2,p,p為奇素數.
由n(G)={1, 3,p+1}及Sylow定理知G有唯一的Sylowqi-子群, 即Qi?_G.若Qi非循環, 因為Qi/Φ(Qi)含有(qi,qi)-型初等交換群, 則Qi至少含有qi+1個極大子群.由引理1知, 這類子群的個數至少有1+kqi個, 其中k≥1.顯然, 1+kqi≠p+1, 矛盾.從而Qi循環且正規于G.
步驟1.2P循環或P同構于Cpβ-1×Cp(β≥2)或〈a,b|apβ-1= 1,bp= 1,b-1ab=a1+pβ-2〉(β≥3).
若P循環, 則P的各階子群只有1個, 因而np=1,p+1.
若P不循環, 則P?_G.否則,P/Φ(P)含有(p,p)-型初等交換群, 即P至少含有p+1個極大子群, 由n(G)={1, 3,p+1}及引理1知P恰含有p+1個極大子群, 而np=p+1, 于是所有Sylowp-子群有多于p+1個不同的極大子群, 矛盾.故P?_G.由于Sk(P)≡1(modp), 知n(P)={1,p+1}.于是由引理3得P同構于Cpβ-1×Cp(β≥2)或〈a,b|apβ-1= 1,bp= 1,b-1ab=a1+pβ-2〉(β≥3).
步驟1.3P2循環或P2同構于下述群之一:C2α-1×C2(α≥2), 〈a,b|a2α-1= 1,b2= 1,b-1ab=a1+2α-2〉(α≥4),Q8.
若P2循環, 則P2的各階子群只有1個, 因而n3=1,3.
若P2不循環, 則P2?_G.否則,P2/Φ(P2)含有(2, 2)-型初等交換群, 即P2至少含有3個極大子群, 由n(G)={1, 3,p+1}及引理1知P2恰含有3個極大子群, 而n3= 3, 于是所有Sylow 2-子群至少含有6個不同的極大子群.由引理1知, 這類子群個數為1+ 2t≥6且為奇數, 矛盾.故P2?_G.由Sk(P2)≡1(mod 2), 知n(P2)= {1, 3}.于是由引理3得P2同構于C2α-1×C2(α≥2), 〈a,b|a2α-1=1,b2=1,b-1ab=a1+2α-2〉(α≥4)或Q8.
步驟1.4P2,P在G中不可能全都正規.
易知, 當q≠2,p時,G的所有Sylowq-子群都循環且正規.故只需討論G的Sylow 2-子群P2與Sylowp-子群P, 再分3種情形討論:
若P2,P都循環且正規, 則G循環,n(G)={1}, 矛盾.
若P2,P有且只有一個循環但都正規.當P2循環且正規時, 由步驟1.2推知,n(G)={1,p+1}, 矛盾于n(G)={1, 3,p+1}; 當P循環且正規時, 由步驟1.3推知,n(G)={1, 3}, 這與n(G)={1, 3,p+1}矛盾.
若P2,P都不循環.由步驟1.2與步驟1.3知,P2?_G,P?_G.則P2P=P2×P≤G=P2×P×Q1×… ×Qn.若P2Q8, 因為G中含有2階子群與p階子群, 所以G中必含有2p階子群, 且2p階子群個數為3(p+1), 矛盾于n(G)={1, 3,p+ 1}; 若P2?Q8, 因為Q8有1個2階子群, 3個4階子群, 所以G中含有4階子群與p階子群.故G中必含有4p階子群, 且4p階子群個數為3(p+1), 這與n(G)={1, 3,p+1}矛盾.于是P2,P在G中不能全部正規.
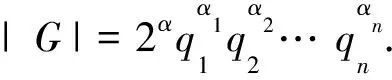
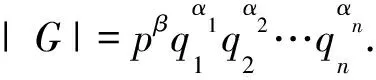
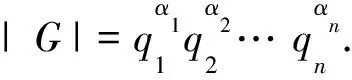
由此可知α>0,β>0.證畢.
推論1設G是有限群, 若G滿足定理1的條件, 則G非冪零.
這是因為若G冪零, 則G的所有Sylow-子群都正規, 顯然矛盾.于是推論1成立.

