基于多蟻群系統的多無人機反偵察航跡規劃

賈雨薇,邵 忻

(天津外國語大學,天津 300011)

0 引 言

隨著無人機技術的發展,無人機偵察已成為當前海上態勢感知的重要途徑之一。

無人機偵察具備機動性好、定位精度高、準備時間短的優勢,能有效克服傳統航天偵察過境時間有限、技術偵察無法確定電磁靜默目標的缺點。多無人機協同目標搜索是多無人機聯合實施的重要任務。在大型搜索區域,當任務繁重和時間緊張時,單架無人機顯然無法快速完成搜索任務,而多架無人機可以有效地完成搜索任務。如今,反無人機防空武器的綜合運用給戰爭中的預警探測和攔截打擊帶來了一些技術挑戰[1]。

1 研究背景

無人機航路選擇成為發現目標的關鍵,因為目標在搜索空間中以一定的概率出現。DM Geletko,AT Davari 等人針對多無人機在同一區域內進行搜索的情況,提出了一種分布式協同控制算法。其主要思想是整合簡單的規則,使它們相互關聯,從而產生復雜的行為。通過半實物仿真演示,多架無人機可完成高度獨立、自主飛行。針對多無人機搜索,設計了隨機搜索、航空搜索和網格搜索3種搜索策略。

袁廣進等人使用多蟻群系統解決多無人機搜索問題。不同的蟻群釋放不同的信息素,并且產生相互排斥的效果。每個蟻群中的所有螞蟻在完成搜索時都會更新信息素,通過最大最小蟻群算法防止信息素過度揮發或積累,并根據搜索概率的模型調整搜索路徑。仿真實驗結果顯示,這種算法很好地完成了多架無人機之間的協作。

同時,如果區域面積較大,少量無人機難以在規定時間內完成既定搜索任務,也可以考慮增加無人機數量。劉永蘭等人提出利用狼群算法解決無人機航路規劃問題,構建無人機在航路規劃中可能遇到的障礙模型。以地形障礙和局部威脅模擬為山峰,抽象出3種捕食行為,即行走、召喚和攻擊。游走行為相當于找到解空間,增加解的多樣性。呼叫行為相當于逼近最優路線,在單架無人機難以完成任務時呼叫協作伙伴,從而提高任務完成概率。攻擊行為相當于集中在最佳路線上,提高了算法的收斂性。仿真結果表明,該航路能夠在較短時間內成功避開障礙物并找到搜索目標。

2 問題的提出

2.1 場景規劃

假設紅方部署2類無人機,分別為低速長續航的U1類無人機與高速短續航的U2類無人機,使用合成孔徑雷達對潛伏在某海域內刺探紅方情報的藍方電子偵察船開展搜索,以期在限定時間內發現和驅離藍方目標,保護紅方信息安全。

2.2 航路規劃

假定在藍方電子偵察船進入偵察位置后,紅方4架固定型號無人機按指定路線對可疑海域開展搜索,其中紅方限制如下:

(1) 搜索時間為3 h;

(2) 每種型號無人機有且僅有2架;

(3) 無人機初始位置為A1、A2機場;

(4) 保證3 h后發現目標概率最大;

(5) 適時考慮返航。

藍方約束如下:

(1) 按照給定概率在指定海域出現;

(2) 機動半徑為10 km。

3 基本假設

假設1:在偵察陣位為1 000 km×1 000 km的區域,將其劃分為1 000×1 000個長寬均為1 km的正方形方里格,由于無人機巡航速度較快,較短時間內的飛行軌跡近似為直線。考慮無人機1個步長時間只移動1個單元方里格,且受無人機機動條件的影響,每次移動均存在3種不同的運動。運動方式為按照巡航速度直線勻速運動,且每次步長移動位置均為方里格中心點,如圖1所示。

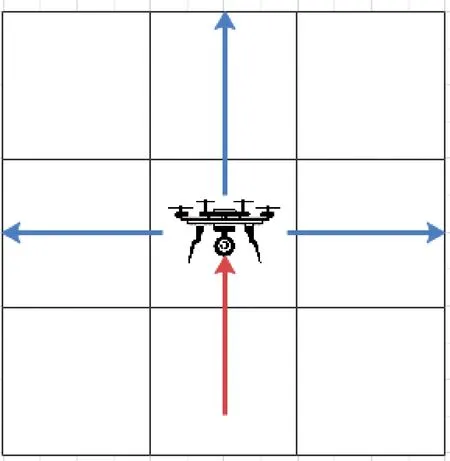
圖1 無人機航行方向圖

假設2:考慮藍方偵察船到達偵察陣位后,會進行半徑為10 km的機動,假設其圓心點位于方里格中心位置。

假設3:無人機每隔20 s進行一次拍照,因此將移動時間間隔設置為20 s,即無人機偵察照相始終開啟,保持每20 s 1次的拍攝狀態,且不影響續航時長。

假設4:無人機和船機動時保持勻速運動,即轉彎與直行保持同速,均保持最大航行速度。

4 問題的模型建立與求解

4.1 問題分析

基于已經給定的藍方偵察船出現概率圖等,并且告知了無人機發現目標概率的計算方法,考慮藍方偵察船會以10 km的半徑進行機動,這將影響其在周邊范圍出現的概率。所以需要考慮偵察船對概率圖的更新,同時考慮無人機搜索對概率圖的更新。概率圖如圖2所示,圖中的顏色越深,代表目標在該區域出現的概率越大,要找尋最優路徑,首先要考慮單個無人機對于發現目標概率的模型,以及確定優化目標。其次考慮多架飛機的協同搜索問題,盡量保證多架無人機的搜索范圍覆蓋面最大,即4架無人機的搜索路徑盡量不交叉[2]。

圖2 目標出現概率熱圖

需要規劃合適的搜索路線,計算路徑中的每個節點(步)的概率,并保證搜索路線中發現概率之和最大。考慮巡航續航時長U1型8 h,U2型4 h,均具有持續搜索3 h的能力,對于8 h巡航無人機可以不考慮其返航,考慮4 h的無人機在巡航3 h后,若與機場航向較遠,即直線距離大于620 km,不能返航。采用離散化的方式將搜索時間離散化為一系列的離散時間點{1,2,…,T}。無人機在每個網格內停留的時間為ΔT,并完成對當前網格的搜索。在相鄰的時間點上,飛行器由當前網格移至與之相鄰的網格[3]。

無人機的基本參數如表1所示。

表1 紅方無人機基本參數表

由于路線計時單位為s,為了便于計算,將巡航速度化為km/s,U1的速度約等于0.889 km/s,U2的速度為1.778 km/s,U2毎橫向或者縱向移動1格的時間為5.63 s,毎斜線移動1格的距離所耗費的時間為11.2 s。

4.2 模型構建

4.2.1 偵察船運動對概率圖的影響更新

結合概率熱圖以及題中所給的目標船機動半徑,假設其在圓形區域內出現的概率服從均勻分布,并且每個方格出現的概率值相等。對各方里格的目標出現概率進行更新,該點目標出現的概率值為其附近10 km內其余方里格機動距離的疊加,近似為20×20的大方里格,除去頂角的20×4個單位方里格,如圖3所示。

圖3 目標概率更新示意圖

目標出現概率更新為:

(1)

最后將更新的概率進行歸一化:

(2)

得到最終目標出現概率模型[4]。

4.2.2 基于Bayes的無人機發現概率更新

無人機當前所在方里格的發現概率為以方里格為中心、探測距離為半徑為R的圓形區域。其中目標在m個方里格中被發現的概率滿足:

(3)

式中:zk=D,表示k時刻的探測事件,則zk=D為未探測事件且滿足:

(4)

無人機在觀測事件發生后,可根據 Bayes公式更新無人機的目標概率圖,為:

(5)

式中:λ為歸一化因子,使得任務海域所有柵格的目標概率之和為1。

4.2.3 優化目標函數

構建目標優化函數為:

(6)

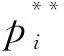
其中航行距離約束為:Du1≤620。

路線約束為:S1∩S2∩S3∩S4=?。

4.3 問題的求解

4.3.1 多蟻群系統優化算法簡介

自組織行為仿生算法是解決優化問題的可靠方法,具有極強的魯棒性和收斂性,而蟻群算法是自組織行為仿生算法中最引人注目的算法,它通過模擬蟻群在覓食過程中總能找到從蟻巢到食物源的最短路徑構建求解路徑。蟻群系統算法是對蟻群算法的改進,可以用于解決偽隨機路徑規劃,也適用于具有先驗概率的路徑求解問題,適用于本題中具有概率圖的路徑尋優問題。

多類型蟻群算法是對單蟻群算法的改進,其增加了不同類型蟻群之間的互斥作用,增加了互斥路徑的優化搜索實驗。多蟻群算法因具有協調性與并行性、正負反饋機制以及強啟發性而成功應用于航跡初始化。這一性質非常適用于多個無人機求解最優路徑,滿足各路徑盡量不重疊的要求。

本文將多蟻群系統算法應用于解決多無人機協同目標搜索問題。將單個執行搜索任務的無人機模擬為1個蟻群系統,同一螞蟻群體內部通過信息素引導個體趨向最優路徑,來自不同螞蟻種群之間的信息素相互排斥實現不同無人機之間的競爭,以避免多架無人機搜索相同區域造成無效搜索[5-7]。

4.3.2 多蟻群協同搜索算法的基本步驟

多蟻群協同搜索算法流程如圖4所示。

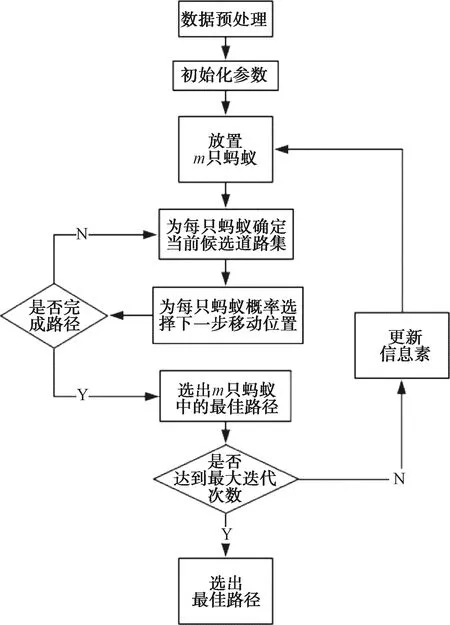
圖4 算法流程圖

假設有n架無人機執行協同搜索任務,每架無人機對應1個螞蟻種群,每個種群由m只螞蟻組成。

首先對搜索區域的所有網格給出合適的信息素初始值。再將全部螞蟻放在所在種群的路徑初始點,一起同時在搜索區域內移動。每只螞蟻在行進中根據狀態轉移規則選擇相鄰的可行網格,直至全部螞蟻完成一次路徑搜索,即完成一次循環。

循環完成后依據各只螞蟻經過路徑進行全局信息素更新,對沒有經過的網格只進行信息素揮發。重復這個過程,直到求出優化路徑。

4.3.3 多蟻群系統算法在本題中的具體實現

(1) 信息素的初始化

信息素分布在每個網格內,每個網格內的信息素初始值為τ0。螞蟻從S點開始搜索,每一步搜索范圍是與其當前所在網格鄰近的滿足機動條件的4個網格。

(2) 路徑選擇策略

第k個種群的螞蟻l選擇新可行節點的概率是由兩節點間邊的代價、自身所在種群信息素的強度以及其它種群信息激素的強度決定的,下式給出了從網格i轉移到可行網格j的概率:

(7)

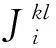
(3) 信息素的更新策略

在所有群體中所有的螞蟻都完成一次搜索后,網格j內第k個種群的信息素強度按下式更新:

τjk(t+1)=(1-ρ)·τjk(t)+ρΔτjk(t+1)

(8)

式中:τjk(t+1) 和τjk(t) 分別為更新前后網格j內第k個種群的信息素含量的強度值;ρ為信息素揮發系數;Δτjk(t+1)為網格j內信息素強度更新值,定義為:

(9)

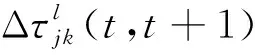
(10)

(11)

式中:Q為信息素強度;Pkl為第k個種群的第l只螞蟻在第t次搜索后所經過的網格內目標出現概率之和,代表了該條路徑的適應值(搜索概率),搜索概率越大,增強值越大;λkl和πkl分別是第k個種群的第l只螞蟻在第t次搜索后所經過的網格內第k個種群信息素的總量和其它種群信息素總量的均值,λkl/πkl代表該條路徑和其它螞蟻種群所搜索的路徑的交疊程度,λkl/πkl越大,交疊越小,增強值越大。

5 仿真實驗

5.1 仿真實驗架構

結合本問題需要的模塊,構建仿真系統需考慮的整體框架,其中包括無人機類、系統環境類、偵察船類3個重要組成部分,無人機類中集成多蟻群系統算法進行搜索路線的規劃和尋優,如圖5所示。

圖5 仿真系統運行概念圖

在仿真建模過程中,基于面向對象技術,設置無人機類、偵察船類以及戰場環境類,每個類中包含各個模塊的屬性和功能,以最大程度地還原問題題意,如圖6所示。

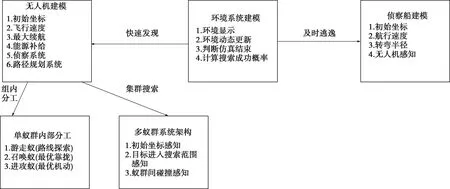
圖6 系統架構圖

其中無人機建模融入多蟻群系統尋路算法,設置2個不同類型的無人機類,分別模擬無人機U1和U2,不同無人機間路徑存在互斥,偵察船類考慮其對概率圖的影響,設置概率圖的更新。環境系統類則對路線進行繪制,對搜索概率進行計算,并進行可視化展示。

5.2 仿真實驗結果

由圖7可得,U1無人機路徑節點為1 080個,U2型無人機路徑節點達到2 160個,由路徑仿真圖可知,符合本文假設的運動限制及下一時刻的運動方向為向前、左轉和后退,4架無人機的軌跡滿足不交叉的限制條件,且續航較短的無人機U2最終位置與起始位置距離小于620 km,達到要求。最終的搜索成功率達到89.4%。

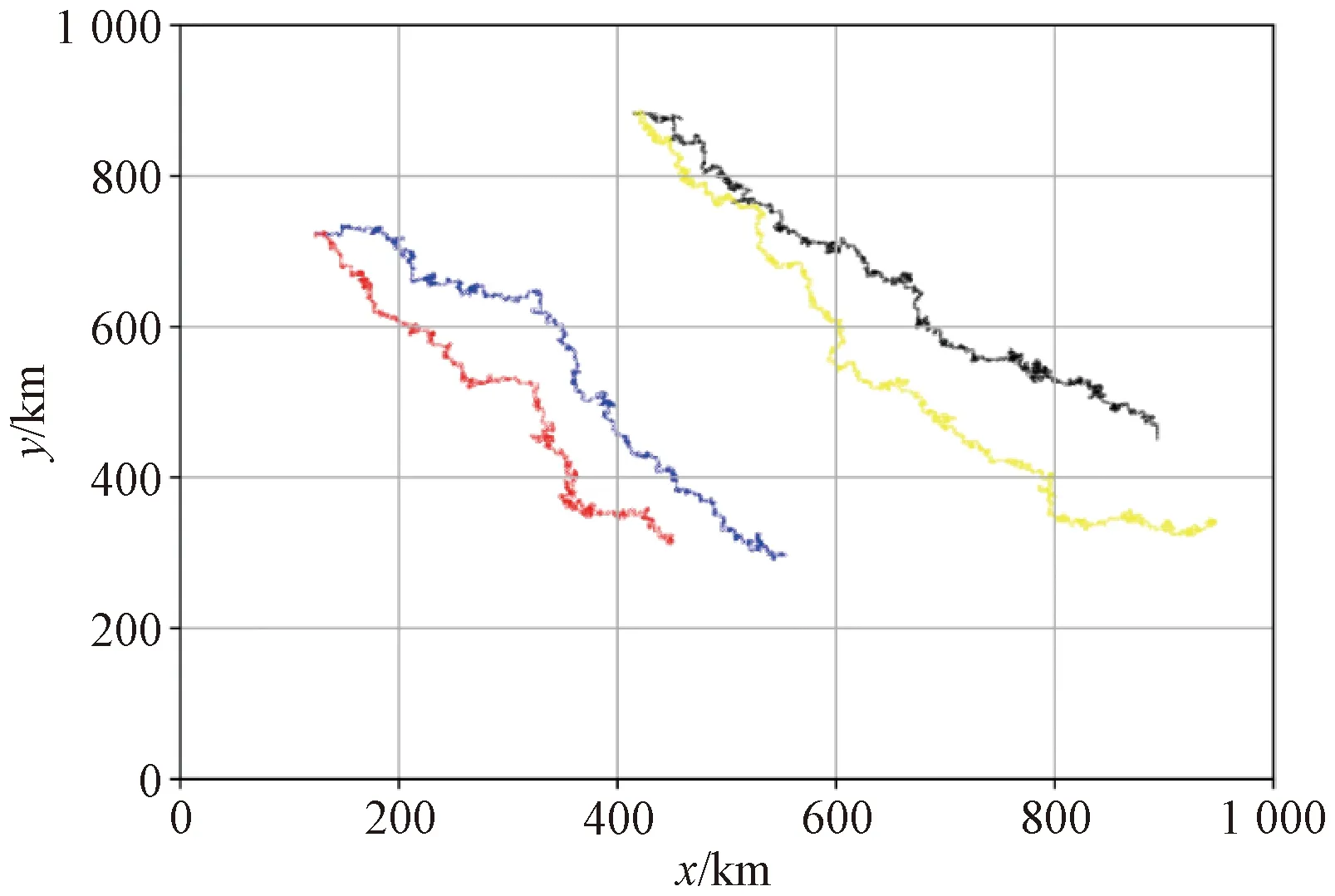
圖7 仿真實驗結果

6 結束語

對于路徑選擇優化問題,首先對無人機與電子偵察船機動策略進行數學建模,根據無人機搜索情況,動態更新概率圖,同時采取Markov Mento-Carlo仿真確定偵察船位置變化。而后通過多蟻群系統算法進行無交叉搜索尋優,確定多架無人機偵察路線。

對偵察陣位地圖進行了離散化處理,假設偵察船在其活動范圍內位置變化服從均勻分布,要求紅方在3 h內規劃航線,使得發現藍方偵察船的概率最大,采用“多類型蟻群系統”算法對路徑進行了尋優,同時考慮了多個無人機之間的路徑堆疊問題,使多個無人機的搜索范圍盡量不交叉,以此保證搜索到目標的概率更大。搜索過程中根據無人機的搜索情況,依據貝葉斯公式對概率圖進行更新,并最終進行了仿真實驗驗證。

針對問題,本文首先假設偵察船在偵察陣位出現以后移動呈現均勻分布,借此更新初始概率圖,并根據無人機的機動進行概率圖的貝葉斯更新。同時提出了“多蟻群系統”算法,該算法引入了不同種群蟻群間的信息素抑制,既解決了路徑堆疊的問題,擴大了搜索的范圍,又能滿足搜索目標的概率最大。最后進行仿真驗證,最大搜索概率達到89.4%。