一種改進型KB-RLS算法在自適應干擾對消中的仿真分析
王鐸澎,黃 華,張生鳳
(中國船舶集團有限公司第八研究院,江蘇 揚州 225101)
0 引 言
在日益惡劣的電子對抗環境中,現代一體化電子對抗平臺在實際工作中不可避免地需要面對強自干擾導致的傳輸誤碼率增加、接收信噪比惡化乃至接收飽和系統自激等問題[1-2]。在針對收發系統間的強自干擾進行抑制的過程中,通常的抑制方法有3種:天線對消、射頻對消和數字對消[3-7]。天線對消通過對系統收發天線的設計增加系統隔離度,進而對自干擾進行抑制,如文獻[3]針對不同天線距離和不同信號頻帶,對不同傳播模式下的天線對消效果進行了討論。射頻對消則是通過構造射頻模擬電路,構造與干擾反相的信號來抵消干擾,在已有的研究中,如文獻[4]在射頻域,針對500 MHz的電磁信號,設計模擬抑制電路,取得22~40 dB的抑制效果。但是,收發系統間的強自干擾經過天線對消和射頻對消后,雖然消除了自干擾信號中的主要部分,殘余的多徑成分與射頻干擾抵消引入的非線性成分仍會影響期望信號的解調[5],還需要數字域干擾抑制技術進一步提升系統的自干擾抑制能力。數字域自干擾對消是指對AD采樣后的數字信號進行對消處理,如文獻[6]利用自干擾信道重建自干擾抑制的方法,通過自干擾信道估計和自干擾信號重建,在數字域最高取得了55 dB的干擾抑制效果。在整個自干擾對消的過程中,為了保證對強自干擾最終的抑制效果,如何在數字域這道最后的防線進行充分的對消,便具有極為重要的研究價值[7]。
目前已有的研究中,數字域自干擾對消技術主要有自干擾信道估計重建對消和自適應濾波對消方法2種[8-13]。自干擾信道估計重建對消主要是利用各類算法在時域或頻域估計出自干擾信道后進行自干擾重建抵消;另一種數字域自適應濾波自干擾抑制則是通過在數字域對自干擾信號進行自適應濾波之后,進行自干擾抑制。文獻[8]利用自干擾信道估計的方法在頻域針對15 dB干噪比的萊斯噪聲,取得最高22 dB的抑制效果。通過對文獻[8]、[9]的對比分析得到,自干擾信道重建自干擾抑制方法雖然能取得較好的干擾抑制效果,但參考具體的算法流程,該方法較為復雜且運算參量較多,不適合工程實現,而目前已有的工程應用則主要是針對自適應濾波自干擾對消方法進行展開[10-13]。
在常見已有的自適應濾波自干擾對消算法研究中,自適應算法主要有遞歸最小二乘(RLS)算法和最小均方(LMS)算法2種,如文獻[10]針對全雙工單通道系統,利用LMS準則下的自適應濾波算法進行對消,取得了20 dB的自干擾抑制效果,但迭代速度緩慢,不滿足電子對抗環境的時效要求。文獻[11]利用經典的RLS算法進行了硬件層面的仿真測試,利用24階的RLS濾波器取得了最大32.16 dB的抑制效果,未能達到預期的對消精度,同時該方案在硬件設計過程中,還有一定的優化空間。文獻[12]則是對RLS算法的計算過程進行改進,利用搜索求解的辦法,針對典型的萊斯噪聲,進行對消測試。該方法雖然降低了RLS算法的求解復雜度,但同時也降低了RLS算法原有的對消精度。文獻[13]則是利用正交三角(QR)分解的方法代替了RLS算法中矩陣求逆的過程,同時設計了Systolic脈動陣列進行仿真對消測試。該方法具有很好的收斂速度和收斂精度,但實際測試中,對信號的輸入具有較高的要求,還需進一步的信號特征分析和算法改進。對上述研究[10-13]中的算法處理過程進行比較,得到LMS及改進算法。由于算法本身的特點,其收斂速度受到一定限制,不適合該場景下的工程應用。經典RLS及相關的改進算法雖然可以滿足收斂速度的要求,但未兼顧算法復雜度、收斂精度、收斂速度、魯棒性,對多種信號的適應性等工程實踐的重要關注點,在實際的工程應用中仍不能取得較好的對消效果。
本文在考慮到已有各種自適應算法不足的前提下,對已有的RLS算法迭代過程進行具體討論,并針對收發系統間的強自干擾提出一種新的改進型RLS算法。該RLS改進算法對算法迭代過程中的收斂因子和自相關矩陣的迭代計算過程進行改進,進而兼顧算法的收斂速度、魯棒性等重要關注點,進一步提高了RLS算法在自干擾對消應用中的適應性和穩定性。
1 算法模型分析
對于常見的自適應濾波自干擾對消系統,系統主要結構如圖1所示,發射干擾信號功分成2路:一路作為輸入信號x(n)進入濾波器;一路作為參考信號d(n),經過整條發射鏈路后進入濾波器。輸入信號擬合出重建信號y(n)后對參考信號進行抵消,最后達到抵消自干擾的目的。

圖1 自適應算法自適應濾波結構示意圖
在該系統中,對于M階RLS自適應濾波器,X(n)、W(n)是迭代開始前的輸入信號向量和權值向量,該向量在首次迭代之前進行初始化:
X(n)=[x(n),x(n-1),…,x(n-M-1)]T
(1)
W(n)=[w0(n),w0(n),…,wM-1(n)]
(2)
迭代過程中,計算該次誤差、卡爾曼增益向量和權值迭代系數,其中d(n)為對應的參考信號,λ為大于0小于1的遺忘因子:
e(n)=d(n)-WTX(n)
(3)
(4)
W(n)=W(n-1)+K(n)e(n)
(5)
式中:PMM是自相關信號的迭代矩陣,通常初始化為對角線的M階單位矩陣,迭代計算公式為:
PMM(n-1)]
(6)
至此完成了整個RLS算法的迭代過程。對應的卡爾曼濾波結構中,代價函數為:
(7)
對應的后向誤差為:
δ(n)=d(n)-XT(n)W(n)
(8)
并且根據文獻[14]的推導可知,δ(n)和δ(n-1)等都與輸入噪聲無關。
目前已針對RLS算法進行改進,主要是針對式(2)遺忘因子和式(4)矩陣迭代過程2個部分。
(1) 針對遺忘因子的改進,主要是將遺忘因子改為關于后向誤差的函數,如文獻[15]將遺忘因子改為:
(9)
類似地,文獻[16]將遺忘因子改為:
λ(n)=λmin+1-λmin2L(n)
(10)
L(n)=-round(μe2(n))
(11)
(2) 針對自相關矩陣計算的改進則是為了保證式(3)的卡爾曼增益向量保持非0,在式(4)添加了自干擾項。如文獻[17]中的改進項為:
PMM(n-1)+round(γe(n))]
(12)
但在實際仿真測試后發現,以上的改進都有算法復雜度增加或魯棒性減弱的缺點。
此外,針對式(3)的改進,已有的研究較少且未進行充分討論,故不作說明。
2 算法改進
在自適應自干擾對消問題中,多種復雜的信號有可能超出經典RLS算法的輸入范圍,且在應對接收信號突變時,經典RLS算法和已有的改進算法在迭代時,濾波器系數均易產生較大的當次誤差,引起濾波器系數的變化。
本文提出一種均衡型-遞歸最小二乘法(KB-RLS)算法,以期在保證抵消效果的同時,滿足各個變化方向的要求。其中,算法主要改進的點在于:
(1) 將遺忘因子設置為:
(13)
式中:a,b,c,m為常量,c作為初始因子,保證了收斂因子的最小取值;同時誤差e(n)和前次誤差e(n-1)的引入保證了在不增加運算量的同時,減少了突變信號對濾波器系數的過分影響,同時需保證λ(n)≤1。
(2) 將自干擾項的增加為:
ρ(n)=αIround(γ(e(n)+oe(n-1)))
(14)
式中:γ和o為2次誤差的經驗系數;α為該自干擾項的影響因子;I為單位矩陣;round函數則能保證避免精度過高導致的數值溢出。
在PMM矩陣計算過程中加入自干擾項,同樣引入了當次誤差e(n)和前次誤差e(n-1),同時考慮到算法復雜度的問題,選擇了二元一次項的形式進行設計。
最終改進的KB-RLS算法流程為:
X(n)=[x(n),x(n-1),…,x(n-M-1)]T
W(n)=[w0(n),w0(n),…,wM-1(n)]
ifλ(n)>1,則λ(n)=1
e(n)=d(n)-WTX(n)
W(n)=W(n-1)+K(n)e(n)
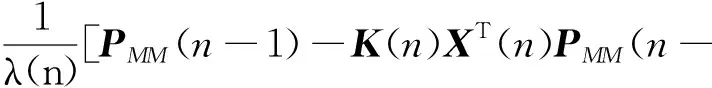
1)+αIround(γ(e(n)+oe(n-1)))]
式中:a,b,m均為調節系數,需實測;在計算迭代矩陣PMM時,γ和o分別為計算自干擾項時2次誤差的經驗系數;α為該自干擾項的影響因子;I為單位矩陣;X(n)為輸入信號序列;d(n)為參考信號序列;e(n)為當次誤差;k(n)為增益向量;W(n)為權植向量;PW為迭代矩陣。
考慮到算法改進可能帶來的運算量增加,將該算法與文獻[17]提到的指數窗截取(EW)-RLS、經典RLS算法進行運算量對比。算法運算資源統計見表1。
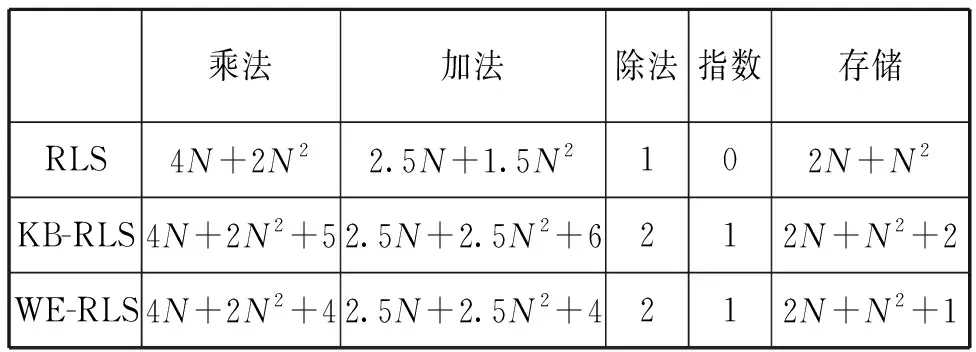
表1 算法運算資源統計表
表1表明,在運算資源方面,改進的KB-RLS算法與另外2種RLS算法保持在同一量級,未過分增加運算資源的消耗。
3 算法仿真
為了驗證該算法的可靠性,本文進行了簡單的算法仿真驗證,并與經典RLS算法和文獻[17]改進的EW-RLS算法進行對比,仿真信號參數見表2。
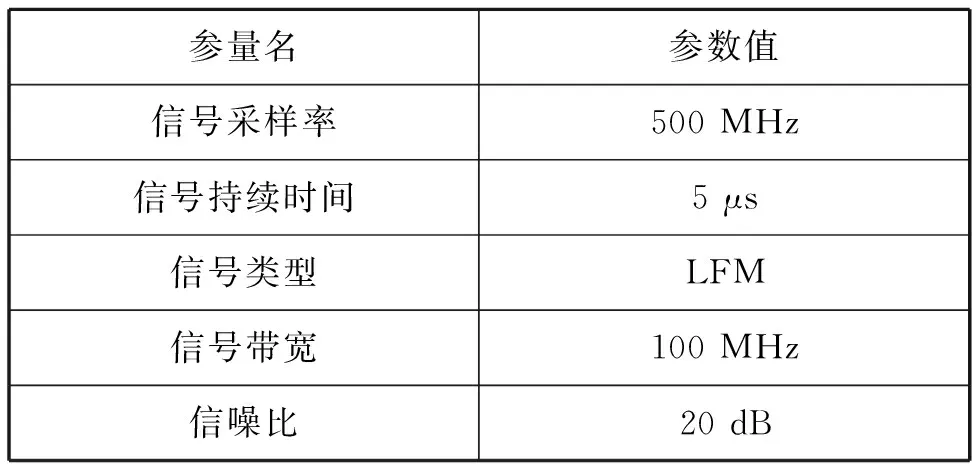
表2 LFM信號測試參數表
該測試信號的時域圖譜和頻域圖譜如圖2所示。
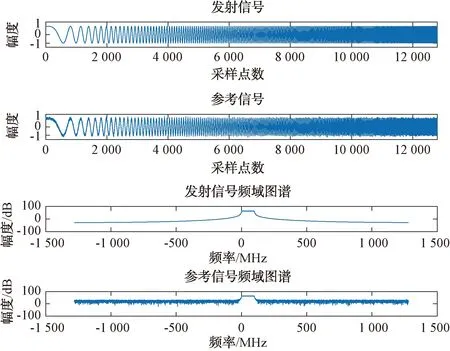
圖2 測試信號時域頻域圖譜
分別利用經典RLS算法、EW-RLS算法和本文提出的算法對該信號進行對消處理,處理過程中3種算法的學習曲線如圖3所示。

圖3 3種算法迭代過程學習曲線
由圖3可見,3種算法在迭代3次后,誤差曲線均降至10-1以下,最終的對消結果見表3。
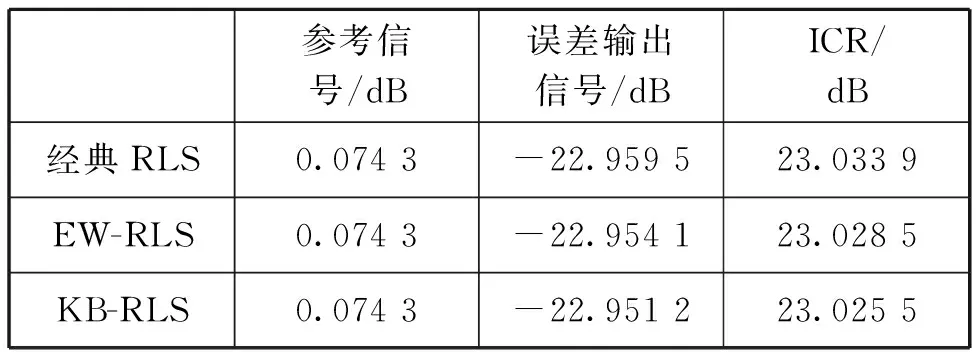
表3 LFM信號對消測試結果統計表
即3種算法對消比為23.033 9 dB、23.028 5 dB、23.025 5 dB,基本保持一致。
對該信號進行多次測試后,繪制測試結果曲線如圖4所示。

圖4 單脈沖LFM信號測試對消結果圖
在該項測試中,KB-RLS算法和經典RLS算法均能保持較好的對消精度,但EW-RLS算法在低信噪比時對消效果較差;此外,在該測試中,KB-RLS算法的對消精度始終高于經典RLS算法。
將該測試信號進行脈沖調制,參數見表4。
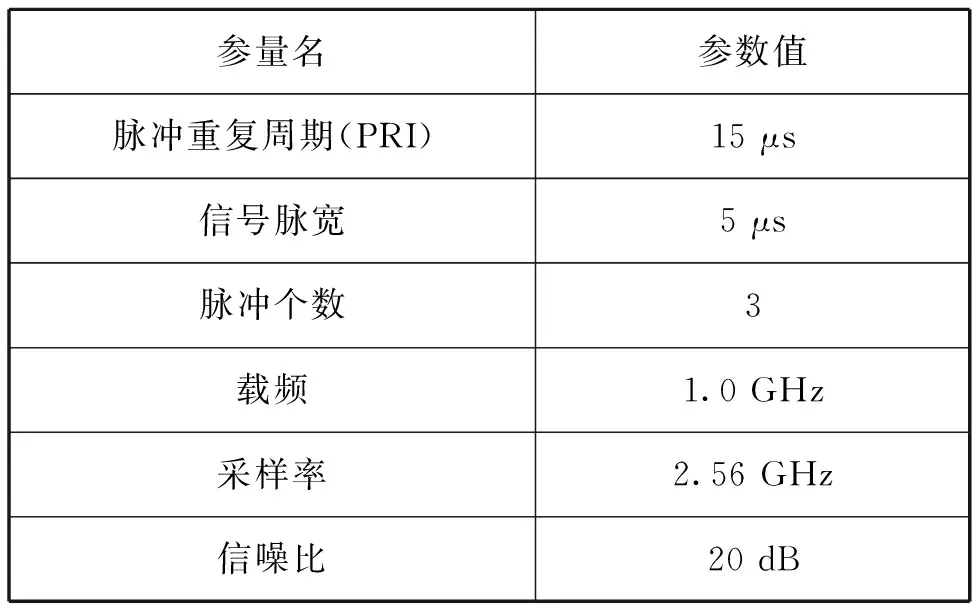
表4 脈沖調制信號測試參數表
再次利用RLS和KB-RLS 2種算法對該測試信號進行對消處理,對消過程中的誤差信號圖譜如圖5所示。

圖5 脈沖信號對消重建、參考信號時頻域圖譜
最終的對消結果則見表5。

表5 脈沖信號對消測試結果統計表
在該次測試下,KB-RLS的對消精度高于RLS算法的對消精度,且在脈沖信號變化時,KB-RLS算法更好地克服了改變帶來的誤差。
同樣地,繪制多脈沖測試下的對消結果,如圖6所示。

圖6 多脈沖LFM信號對消測試結果示意圖
另外,繪制信噪比為10 dB、15 dB、20 dB、25 dB環境下2種算法的誤差曲線,如圖7所示。

圖7 多脈沖LFM信號仿真誤差曲線
對本文的實驗結果進行分析后,得到結論:在本次仿真測試中,KB-RLS算法在保持不輸RLS算法收斂、對消精度的前提下,面對脈沖信號可以更好地克服信號突變帶來的影響。
4 結束語
本文基于已有RLS算法的研究,結合自適應自干擾對消的實際工程需求,在保證一定收斂精度并保持較快的收斂速度,以及保證算法的低復雜度的前提下,對遺忘因子和自干擾項進行優化,提出了一種改進型KB-RLS算法。通過仿真,該算法在進行自適應干擾對消時,不但能獲得高于經典RLS算法的對消結果,更能有效避免輸入信號突變所引起的誤差增大問題。

