船舶擺線推進器水動力性能仿真研究

陳文文，呂 峰，陳 練，劉家昊，張 鋒

(1. 江蘇科技大學 船舶與海洋工程學院, 江蘇 鎮(zhèn)江 212000；2. 中國船舶信息中心, 北京 100101；3. 江南造船(集團)有限責任公司, 上海 201913)

0 引 言

擺線推進器（cycloidal propeller）也稱直翼推進器，它是由一組數(shù)量不等的葉片等間距分布組成，葉片從船體表面伸向水中并與船體表面垂直,同時繞某特定點做圓周運動，由于葉片在空間上的運動軌跡是一條擺線，因此被稱之為擺線推進器。擺線推進器在保持回轉箱轉速恒定的情況下也能快速改變推力的大小和方向，其高效的操縱性使得船舶能實現(xiàn)側向移動、原地回轉等一系列高難度的動作，安裝了擺線推進器的船舶在低速航行狀態(tài)下的控制力也大大提高。

擺線推進器近些年來的研究主要分為2 個階段理論研究和實驗研究。在實驗研究階段，張洪雨[1]利用設計的偏心盤-偏心率-連桿機構實驗裝置研究了不同方向角、偏心率等工況下擺線推進器的水動力性能變化。段瑞[2]設計了一種偏角可控直葉片擺線推進器的試驗裝置，計算了葉片在不同狀態(tài)下的推力系數(shù)，扭矩系數(shù)，并依據(jù)葉片的非定常效應以及葉片之間的相互干擾，對計算結果進行修正。陳先進[3]提出了一種曲柄滑塊機構，并將其應用在擺線推進器上,相比于傳統(tǒng)的擺線推進器，其具有高效、結構簡單、螺距連續(xù)可調的優(yōu)點。在理論研究階段，谷口中[4]提出一套適用于實際應用中的理論模型，并利用動量定理，對誘導速度的計算公式進行了經(jīng)驗補充。Nakonechny等[5]通過對大量實驗值的分析，得出谷口中法的適用范圍為中小進速系數(shù)，當進速系數(shù)較大時，得到的計算值與實驗值誤差偏大。朱典明[6]以此為基礎，對谷口中的計算方法進行了優(yōu)化，從而提高了計算結果的準確度。顧欣星[7]利用滑移網(wǎng)格建立擺線推進器的水動力性能模擬方案，依靠研究的結果對擺線推進器的葉片翼型等結構參數(shù)進行優(yōu)化，總結葉片翼型變化對推進器推進效率的影響。

本文選取和NSRDC 實驗中翼型相近的NACA 3 412翼型，對仿真方法的可靠性進行驗證，基于驗證的CFD 的數(shù)值模擬方法，分析進速系數(shù)以及偏心率變化對擺線推進器的性能影響，并總結了不同初相位下葉片之間的受力變化趨勢。

1 擺線推進器的工作原理

擺線推進器工作過程中，葉片隨著推進器葉輪做圓周運動，葉片本身還在做升沉擺動，擺動運動的中心點是葉片的自轉中心點，2 種運動的合運動為擺線運動。

葉片隨著擺線推進器轉輪旋轉時，所有葉片弦線的垂線始終匯交于一個點，即滿足“法線相交定律”，如圖1 所示。相交的這個點稱為偏心點N。擺線推進器葉片的受力是升力與阻力的疊加，2 個力的合方向垂直于偏心ON，所以通過移動偏心點N 的位置，可以改變葉片和來流方向之間的角度，這就是調節(jié)擺線推進器推力方向的原理。

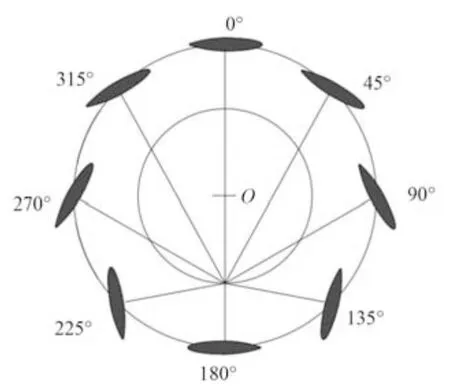
圖1 擺線推進器葉片運動原理Fig. 1 Motion principle of cycloid propeller blades

若當葉片的弦線始終與擺線圓周軌跡的切線方向保持同向，擺線推進器將不會產(chǎn)生推力，此時推進器轉動1 周前進的距離稱為擺線推進器的螺距。當改變偏心點N 的方向時，相當于在葉片與軌跡線的夾角上增加或減小了1 個角度，從而可以改變推力的大小和方向，葉片在1 個周期內的運動軌跡如圖2 所示。

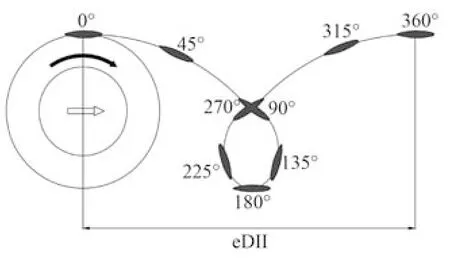
圖2 擺線推進器葉片軌跡示意圖Fig. 2 Geoid propeller blade track schematics

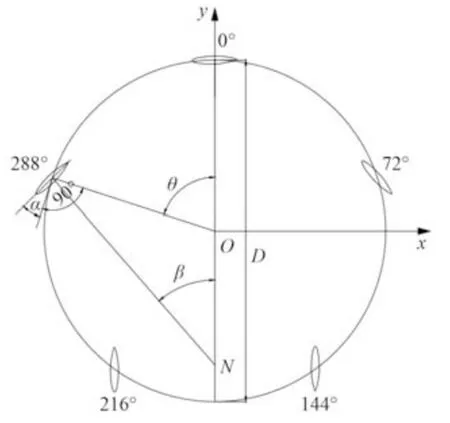
圖3 擺線推進器的運動模型Fig. 3 Motion model of cycloid propeller

擺線推進器旋轉中心點為O 點，點O 和點N 之間ON 的距離稱為偏心距。葉片弦線與葉片自轉中心點處圓周切線之間的夾角為α，葉片自轉中心點和偏心點N 之間的連線與直線ON 之間的夾角為β。根據(jù)外角定理可得：

通過數(shù)學關系求解可得：

根據(jù)定義，角α對時間t求導,即為葉片的自轉角速度，可求得角a′

2 數(shù)學模型

2.1 三維模型

選取NACA 0012 翼型作為擺線推進器葉片模型，葉片最大厚度位于29.6% 的翼弦處，最大彎度位于0.0%翼弦處，葉片翼型如圖4(a)所示。選取CATIA 軟件對推進器進行建模，擺線推進器模型如圖4(b) 所示，推進器模型的主要參數(shù)如表1 所示。

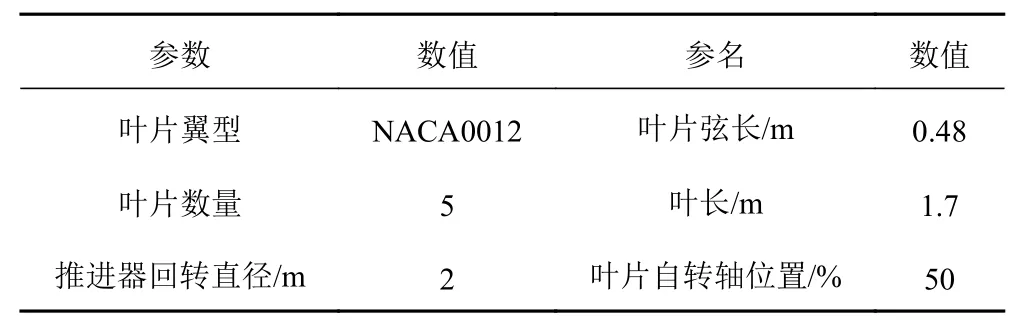
表1 推進器模型參數(shù)Tab. 1 Propeller model parameters

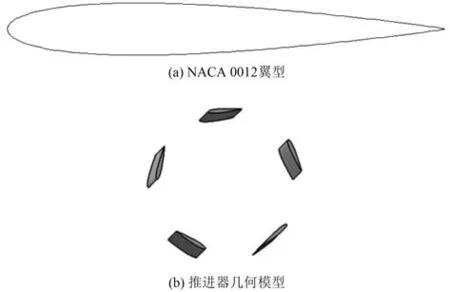
圖4 葉片翼型及推進器幾何模型Fig. 4 Geometric model of blade airfoil and propeller

2.2 控制方程

擺線推進器前進時的運動速度較小，其周圍的流體可看作不可壓縮流體，其滿足質量守恒定律的同時，也滿足N-S 方程。

其中：ρ表示流體介質的密度；t表示物理時間；p為壓力；u，v和w分別為流體速度在x，y和z方向上的分量；X，Y和Z為微元體質量力的分量。

3 計算域和網(wǎng)格

3.1 邊界條件及初始條件

擺線推進器葉片的運動是自轉和公轉的疊加運動，較為復雜，因此需要優(yōu)化CFD 計算方案研究擺線推進器的敞水性能。利用STAR-CCM+中重疊網(wǎng)格模擬葉片自轉和繞葉輪公轉的運動。選取的計算域為一圓柱體，計算域的范圍是以推進器的公轉軸為中心，靠前端5 m，靠后端12 m，計算域半徑為5 m，計算域的邊界選取的足夠大，以減小邊界效應對計算精度的影響。擺線推進器的計算域由靜止域和旋轉域組成，靜止域用于模擬流體的平面流動，旋轉域用于模擬擺線推進器葉片復雜的運動。

有關邊界條件的設定如圖5 所示，邊界類型分為速度進口、壓力出口、對稱平面。流場的入口設定為速度進口，流場出口設定為壓力出口，流場側邊界設定為對稱平面，葉片的表面類型設定為壁面，5 個圓柱面區(qū)域邊界類型設定為重疊網(wǎng)格，并創(chuàng)建靜止域和各圓柱表面的界面，類型設定為重疊網(wǎng)格。

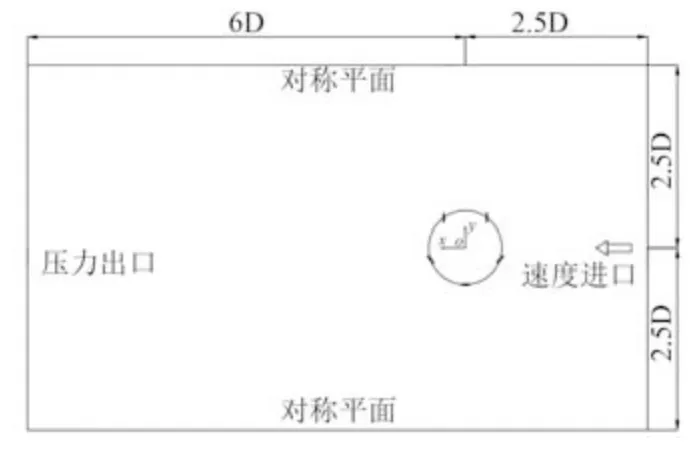
圖5 計算域示意圖Fig. 5 Calculation domain schematics

考慮到葉片翼型以及葉片壁面剪切力的影響，選取SSTk-ω湍流模型, SSTk-ω湍流模型相比k-ε模型，能夠適用于更為復雜的流場，計算結果的可靠性更高[8]。計算域流場的湍流強度和湍流粘度比等參數(shù)設定為軟件默認值，計算時間步長選取為 0.002 s。

3.2 網(wǎng)格劃分

計算域的網(wǎng)格尺寸為0.5 m，葉片自轉中心設置在葉片弦線的中點，葉片的網(wǎng)格尺寸設置為0.03 m，并對各葉片的導邊和隨邊進行加密。以5 個葉片各自的自轉軸為中心，半徑為0.5 m 創(chuàng)建6 個小圓柱體。以各個小圓柱體為目標零部件，與對應的葉片進行減運算得到單個葉片旋轉域。以整個推進器葉輪的旋轉軸為中心軸，對稱建立一個邊長為3.5 m，高度為2.2 m的方形網(wǎng)格加密區(qū)，以保證數(shù)據(jù)交換的穩(wěn)定和計算結果的精確。網(wǎng)格加密區(qū)域包括了擺線推進器的5 個葉片及其旋轉域，加密區(qū)的布局如圖6 所示。通常在進行CFD 仿真分析時，網(wǎng)格越密計算得出的結果就更精確，與此同時工況計算量會加大，相應的仿真時間也會更長。綜合計算結果的精度以及運行時間等因素考慮，加密區(qū)的網(wǎng)格尺寸設置為0.03 m，和5 個葉片旋轉域的網(wǎng)格尺寸相同，以保證數(shù)據(jù)傳輸過程中不會出現(xiàn)太大的波動落差。

圖6 葉片加密區(qū)網(wǎng)格劃分Fig. 6 Grid division in blade-encrypted area

4 計算結果與分析

沿著各個葉片前進方向分解各葉片所受外力，即可得到某瞬態(tài)時刻下的擺線推進器主推力，對一個周期內的平均主推力進行疊加[9]，得

同理，把各槳葉旋轉1 周的平均轉矩進行疊加，得

其中：z表示推進器的葉片數(shù)；T表示擺線推進器產(chǎn)生的主推力；Q表示擺線推進器產(chǎn)生的扭矩；ti(θ)，qi(θ)分別表示葉片軌跡角為θ時的主推力、扭矩。

對以上公式進行無因次化，即可得到推力系數(shù)，扭矩系數(shù)，推進器效率。

式中：J表示進速系數(shù)；ρ表示推進器所處介質的密度；n表示擺線推進器的轉速；D表示擺線推進器的直徑；L表示葉長。其中進速系數(shù)為：

4.1 精度驗證

為了對仿真方法可行性進行驗證，采取和NSRDC 實驗中翼型相近的NACA 3 412，其他參數(shù)與其相同。經(jīng)過對擺線推進器的建模、網(wǎng)格劃分、邊界條件劃分等一系列操作，將所得的仿真值與實驗值進行比較，結果如圖7 所示。

圖7 計算結果與實驗結果對比下的主推力系數(shù)Fig. 7 Main thrust coefficient compared with experimental results

分析可知，當偏心率不變時，主推力系數(shù)KT隨著進速系數(shù)J的增大而減小，同一進速系數(shù)下主推力系數(shù)KT隨著偏心率e 的增大也逐漸增大，當偏心率變化時，KT也會發(fā)生相應的變化，這也是通過改變偏心率進而改變推力的大小和方向的原理。由于偏心率的這個特性，擺線推進器因此具備優(yōu)越的操控性能。同時由于旋轉的葉片翼型和實驗中的葉片截面有所區(qū)別，導致數(shù)值模擬的結果較實驗數(shù)據(jù)偏大，當偏心率e=0.6、進速系數(shù)J=1.6 時，兩者差值最大，出現(xiàn)的一個最大誤差為6.32%，這可能是由于流體的擾動導致的。計算整體結果平均誤差為3.14%，仿真結果與實驗值整體變化趨勢相近，且兩者誤差在允許范圍內，表明仿真方法模擬效果較好，可靠性較高。

4.2 數(shù)值模擬分析

在仿真計算和實驗數(shù)據(jù)對比的基礎上，將擺線推進器的葉片翼型NACA 3412 更改為本文所選取的NACA 0012 翼型，擺線推進器的轉速為42 r/min，進速系數(shù)的范圍為0.5～2.0，同樣在保持偏心率e=0.8，0.7，0.6 等其他參數(shù)不變的情況下，對擺線推進器的敞水性能進行仿真，仿真所得的主推力系數(shù)KT 隨進速系數(shù)J變化的曲線如圖8 所示。

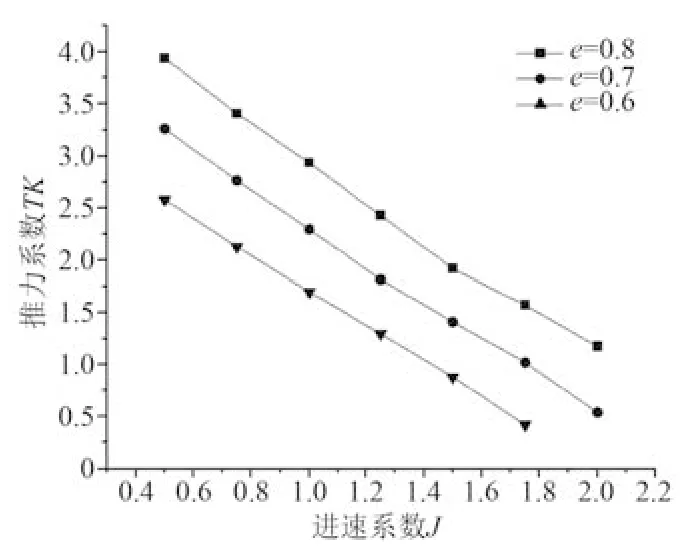
圖8 不同偏心率下的推力系數(shù)曲線Fig. 8 Thrust coefficient curves at different eccentricities

可知，當進速系數(shù)J相同時，KT隨著偏心率e的增大而增大，當偏心率相同時，KT隨著進速系數(shù)J增大而減小。

保持偏心率e分別為0.8，0.7，0.6，其他參數(shù)不變的情況下，仿真所得轉矩系數(shù)KQ隨進速系數(shù)J變化的曲線如圖9 所示。

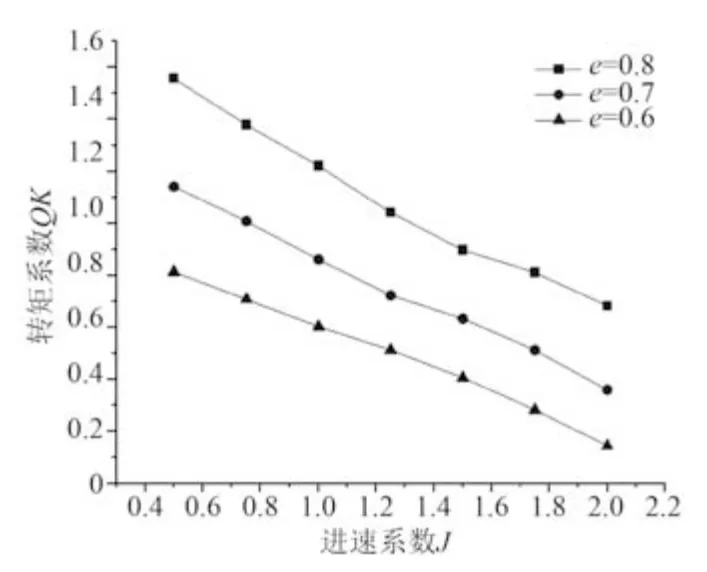
圖9 不同偏心率下的轉矩系數(shù)曲線Fig. 9 Torque coefficient curves at different eccentricities

可知，KQ的變化趨勢和KT類似，當進速系數(shù)J相同時，KQ隨著偏心率e的增大而增大，當偏心率相同時，KQ隨著進速系數(shù)J增大而減小。

為了研究不同初相位下葉片的受力變化規(guī)律,在上述結果里隨機選取了一個工況進行分析。選取的工況參數(shù)為：擺線推進器偏心率e=0.7，進速系數(shù)VA=2.1 m/s。此工況下，各葉片瞬時推力變化幅值曲線如圖10 所示。考慮到計算收斂需要一定的時間，在達到收斂之前推力變化沒有達到穩(wěn)定狀態(tài)，誤差較大，因此選取第2 個旋轉周期即位置角為360°時開始監(jiān)測。

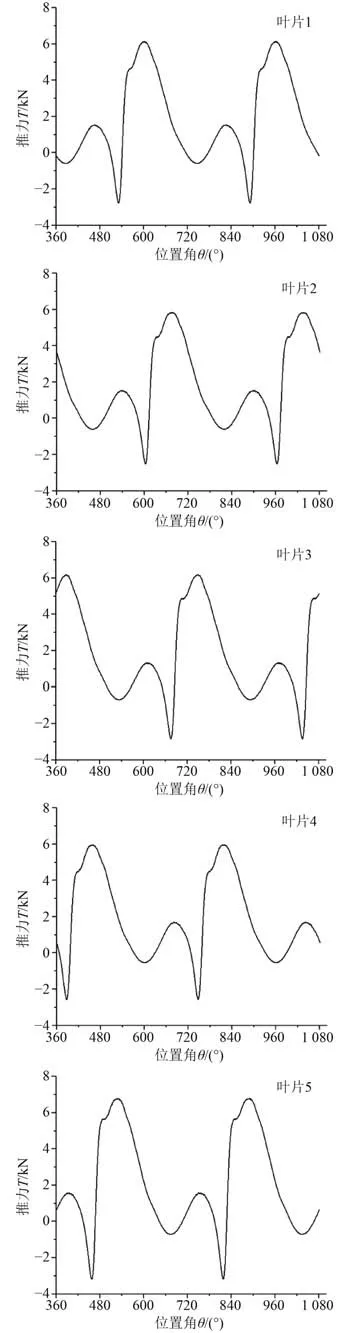
圖10 e=0.7 時各葉片瞬時推力變化曲線Fig. 10 Transient thrust curve of each blade at e=0.7

由圖10 可知，5 個葉片的受力波動趨勢大致相同，只是由于5 個葉片各自存在一個初始相位角差值，導致變化趨勢曲線也間隔一個相位，這個相位正好等于葉片初始相位角差值72°。同時葉片之間的流場存在相互干擾以及葉片自身旋轉的差異性，各推力峰值會產(chǎn)生一定的波動，但整體的變化趨勢依舊相同。

擺線推進器在偏心率e=0.7，進速系數(shù)VA=2.1 m/s時，各葉片瞬時轉矩變化曲線如圖11 所示。規(guī)律與推力變化趨勢曲線相近，5 個葉片受到的轉矩變化趨勢相同，但同樣存在72°的相位差。

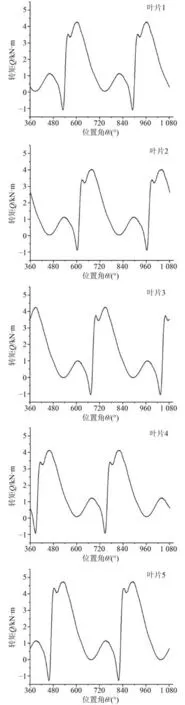
圖11 e=0.7 時各葉片瞬時轉矩變化曲線Fig. 11 Transient torque curve of each blade at e=0.7

在某些角度范圍內，葉片的推力及轉矩會存在負值，但在大部分角度下葉片的推力及轉矩是正值。在1 個旋轉周期內葉片的推力和轉矩均會存在1 個峰值，且正向的峰值較大，此時的瞬時值可以作為葉片強度校核的依據(jù)，同時葉片所受的推力及轉矩都是隨葉輪轉角的變化而變化，變化的周期為360°。

5 結 語

本文對擺線推進器水動力性能的數(shù)值仿真方法進行探討，并采用NACA 3 412 翼型為推進器葉片模型對仿真方法驗證，得出的結果與NSRDC 實驗值進行比較，兩者之間的誤差在允許范圍內，表明仿真得到的計算結果精度較高，驗證了仿真方法的可行性。在此基礎上以自主選用的葉片翼型作為擺線推進器葉片模型，分析偏心率和進速系數(shù)對擺線推進器敞水性能的影響，同時研究了不同初始角葉片之間所受的推力及轉矩變化規(guī)律，得出以下結論：

1） 進速系數(shù)一定時，偏心率越大，推進器的KT、KQ值越大；偏心率一定時，進速系數(shù)越大，推進器的KT、KQ越小。

2） 不同初相位下葉片所受的推力和轉矩變化規(guī)律相同，只是相差了一個初始相位角，同時由于葉片之間的流場存在相互干擾以及葉片自身旋轉的差異性，各推力峰值會產(chǎn)生一定的波動，但整體的變化趨勢依舊相同。