新型薄膜式壓力傳感器的參數設計*

王 昭，吳祖堂，楊 軍，李 焰，劉文祥

（西北核技術研究所強脈沖輻射環境模擬與效應全國重點實驗室，陜西 西安 710024）

在沖擊波壓力測量中，壓電式壓力傳感器在響應頻率、量程和靈敏度等方面具有一定的優勢，得到了大量應用[1-9]。喻健良等[5]、胡宏偉等[6]和黃菊等[9]均利用壓電式壓力傳感器開展了爆炸沖擊波壓力測量，該類傳感器的響應頻率可達300 kHz，壓力測量上限可達200 MPa。盡管如此，約300 kHz 的響應頻率還不能完全滿足爆炸沖擊波壓力測量要求，需要利用動態補償技術提高測試精度[1]。另外，由于采用了壓電類材料作為敏感元件，壓電式傳感器受壓產生的電荷容易泄漏，一般選用準靜態或者動態標定方法來確定其靈敏度系數，增加了靈敏度系數標定的復雜性，且容易引入新的誤差，影響測量精度。而且，壓電式壓力傳感器容易受環境溫度和電磁干擾的影響，難以滿足復雜場景的壓力測量要求。

為滿足強電磁輻射、高溫等極端環境中大量程動態壓力測量要求，王昭等[10-12]提出了一種全新的薄膜式壓力測量方法，用于獲取空氣中沖擊波的反射超壓峰值。與建立在利用待測壓力與敏感元件的形變（或者位移）之間的關系來開展壓力測量的常規傳感技術不同，薄膜式壓力測量方法利用了待測壓力與薄膜加速度之間的正比關系開展壓力測量。與常規壓電式、壓阻式動態壓力傳感器相比，薄膜式壓力測量原理更簡明，具有無需標定、響應時間短、環境適應性強和成本低等優點。

王昭等[11-12]已經開展了激波管驗證實驗，對比研究了薄膜式壓力傳感器與標準壓力傳感器的性能差異，輸出結果驗證了所提出的新型薄膜式壓力測量方法的可行性。但是，激波管裝置產生的沖擊波壓力一般為兆帕量級，難以全面評估薄膜式壓力傳感器的性能。另外，受薄膜式壓力測量原理的限制，難于利用半正弦波發生器等準靜態壓力發生裝置對薄膜式壓力傳感器進行性能驗證。為拓展薄膜式壓力傳感器的應用場景，需要進一步對該傳感器的關鍵參數、量程和測量精度進行探討分析。

本文中，圍繞敏感測壓薄膜開展數值模擬，重點分析薄膜厚度和待測壓力等因素對壓力測量的影響，深入分析數值模擬獲取的數據，優選薄膜厚度，改進數據處理方法，提升薄膜式壓力傳感的測量精度。另外，開展激波管實驗，驗證數值模擬分析的部分結論，為薄膜式壓力測量方法的推廣應用提供參考。

1 數值模擬

測壓薄膜是薄膜式壓力測量方法的敏感元件，測量原理見圖1[12]，圓形薄膜固定在圓柱形套筒端面，受沖擊波的直接作用而產生運動。根據牛頓第二定律可知，薄膜中心區域受到的作用力等于其運動的加速度與質量的乘積，由此可以得到沖擊波壓力。隨著薄膜在壓力作用下運動速度的升高，作用于薄膜的壓力將降低，因此薄膜式壓力傳感器主要用于獲取沖擊波的反射壓力峰值，而不是反射壓力歷程[12]。需要注意，該壓力傳感器一般用于沖擊波正反射的情形，斜入射將對壓力測量精度產生影響。

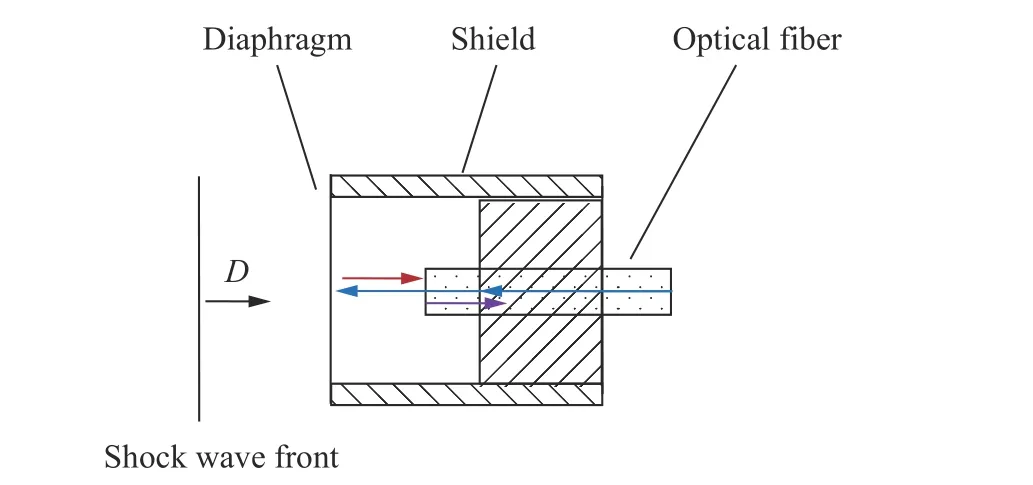
圖1 薄膜式壓力傳感器的原理[12]Fig.1 A principle of a thin diaphragm pressure sensor[12]

影響薄膜式壓力測量的因素較多，主要包括薄膜厚度、待測壓力、數據處理方法、薄膜均勻性和薄膜缺陷等。一般選取工業用不銹鋼薄膜為敏感元件，隨著機械加工精度的提高，不銹鋼薄膜的均勻性和缺陷已經得到有效控制。敏感薄膜在沖擊波壓力作用下從靜止開始運動，運動的薄膜必然受到空氣阻力的作用，運動的薄膜也會導致反射壓力的降低（相對于沖擊波作用在固壁上產生的反射壓力），進而影響壓力測量。薄膜的運動速度主要與薄膜厚度、待測壓力以及作用時間相關，利用理論模型來描述薄膜受沖擊過程較復雜。

另外，薄膜必然會受到邊沿擾動和支撐的影響，而該擾動傳遞至薄膜中心區域需要時間，稱該傳遞時間為薄膜的有效測量時長，有效時長與薄膜的半徑成正比，在有效時長內，可忽略邊沿擾動對中心區域加速度的影響。對薄膜式壓力傳感器的討論均在有效測量時長內展開，當不銹鋼薄膜半徑取8 mm 時，有效時長約2.5 μs[12]。

選用某商業有限元模擬軟件開展數值模擬，獲取不同厚度的不銹鋼薄膜在不同壓力作用下的運動參數數據，以便于開展量化分析。爆炸沖擊波壓力曲線具有陡峭的上升沿，可達納秒量級[13]，對薄膜式壓力傳感器微秒量級的有效測量時間而言，忽略壓力的上升過程，認為壓力是突變的。爆炸沖擊波壓力的下降沿一般呈指數形式下降，持續時間差異較大，一般可達數百微秒及以上。快速的下降沿將對薄膜式壓力傳感器的測量精度產生影響，因而分別采用階躍形沖擊波和爆炸沖擊波2 種加載方式，以量化評估壓力下降對壓力測量的影響。

特別地，在有效時長（微秒時間尺度[12]）內，薄膜的邊沿擾動和支撐還未作用于薄膜中心區域，為了獲得薄膜中心區域在沖擊波作用下的運動歷程，可選取一維模型開展數值模擬，在薄膜的半徑方向上不再劃分網格，以減少運算量。該模擬工作僅估算有效時長內薄膜中心區域的受沖擊過程，在此之后邊沿擾動將對薄膜中心區域產生影響，不能使用一維模型。另外，在沖擊波作用下，圖1 所示傳感器結構中的薄膜容易變形損壞，即制作的薄膜式壓力傳感器不能重復使用，但薄膜的造價低廉，壓力探頭裝配簡單且無需標定，該傳感器仍然具有應用價值[12]。此外，張崇玉等[14]研究發現，1.5 mm 厚的鎢合金飛片受到約40 GPa 的炸藥接觸爆炸壓力作用時，在3 μs 內飛片表面的大部分區域保持完整，未發生破壞。因此，可以推測，對于厚度更小的不銹鋼薄膜，在有效時長內，其中心區域的耐受壓力閾值會進一步增大，可滿足吉帕量級的沖擊波壓力測量要求。

在相同待測壓力和作用時間下，當薄膜厚度很小時，薄膜在短時間內可獲得較高的速度，使薄膜對入射壓力的反射效果減弱，且空氣阻力增大，不利于壓力的精確測量；當薄膜厚度很大時，薄膜在厚度方向上的彈性效應將非常明顯，不利于薄膜運動參數的準確獲得。因此，理論上薄膜的厚度存在優選值。

在材料模型方面，選用理想氣體狀態方程來描述空氣介質，空氣密度取1.22 kg/m3，其絕熱指數根據壓力的不同而變化，對于兆帕量級及以下狀態，絕熱指數取1.4；采用JWL 狀態方程[15]來描述TNT 爆炸產物的膨脹過程，炸藥密度取1630 kg/m3，內能取6.0 GJ/m3；對于不銹鋼，選用Shock 狀態方程和Johnson-Cook 強度模型[16]，以描述爆炸過程中有可能產生的大變形、高應變狀態，密度取7900 kg/m3，體積模量取166 GPa，基礎屈服強度取0.454 GPa，硬化常數取1.96 GPa。

1.1 階躍形沖擊波加載

階躍形沖擊波的輸入相對簡單，可借此精確分析薄膜厚度和待測壓力對壓力測量的影響。采用Euler 網格描述空氣材料，為獲取階躍形沖擊波，這里參考激波管產生階躍壓力的原理開展數值模擬。

建立軸對稱有限元模型，某次模擬，模型長度取100 mm，半徑取10 mm，網格尺寸為50 μm×10 mm，網格數量為2 000×1（即一維模型），對應模型見圖2。修改25 mm 長度空氣材料的初始密度和內能，使之變為高壓空氣；剩余75 mm 長度填充常溫標準空氣。設置相關參數，開始計算，高壓段氣體將迅速向低壓段運動，形成階躍形沖擊波，某時刻的壓力分布見圖3，其中紅色部分為高壓區，藍色部分為常壓區，紅色與藍色之間是沖擊波的形成區。經模擬計算，修改高壓段空氣的初始密度和內能，將改變所形成沖擊波壓力的大小；隨著沖擊波傳播距離的增大，所形成沖擊波壓力平臺的持續時間將延長。

圖2 階躍壓力產生模型Fig.2 Generation model of step pressure

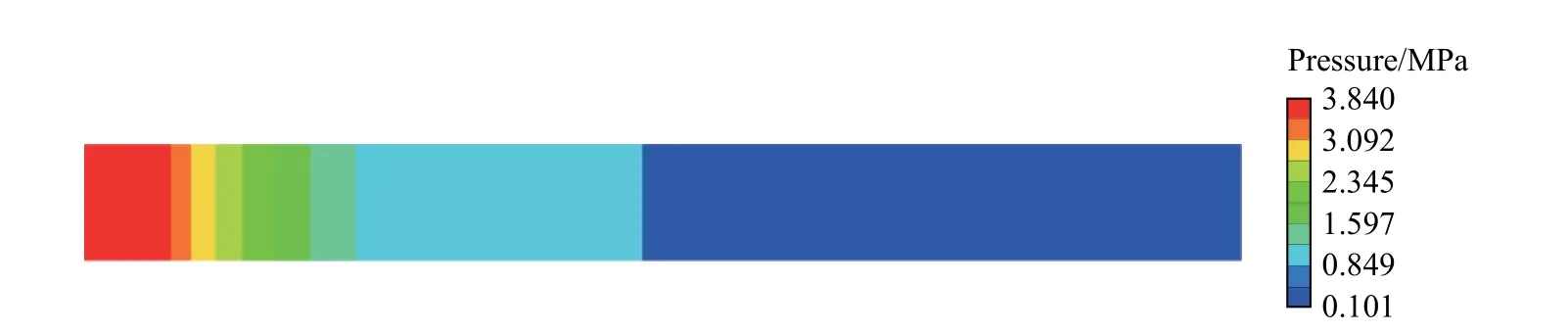
圖3 某時刻的階躍壓力云圖Fig.3 Step-pressure distribution at a certain moment

調節高壓空氣材料的初始密度和內能，獲得4 種入射壓力，依次為0.2392、0.9885、9.927 和107.6 MPa。減小沖擊波方向上的網格尺寸至1 μm，以適應微秒量級厚度不銹鋼與沖擊波之間的流固耦合，在合適的沖擊波形成區域添加不銹鋼材料的Lagrange 網格。約束不銹鋼網格的運動速度為零，可獲得反射壓力，依次為0.5107、4.619、78.05 和1197 MPa，稱為標準反射壓力；不約束薄膜網格的運動狀態，可獲得不同厚度h不銹鋼薄膜在階躍壓力作用下的運動參數歷程，薄膜厚度依次為10、30、50、70 和90 μm。獲得薄膜受沖擊波表面在0.2392 MPa入射壓力作用下的反射壓力見圖4，其中p2為標準反射壓力。獲得薄膜自由面（薄膜的未受到沖擊波壓力直接作用的表面）的運動速度見圖5。

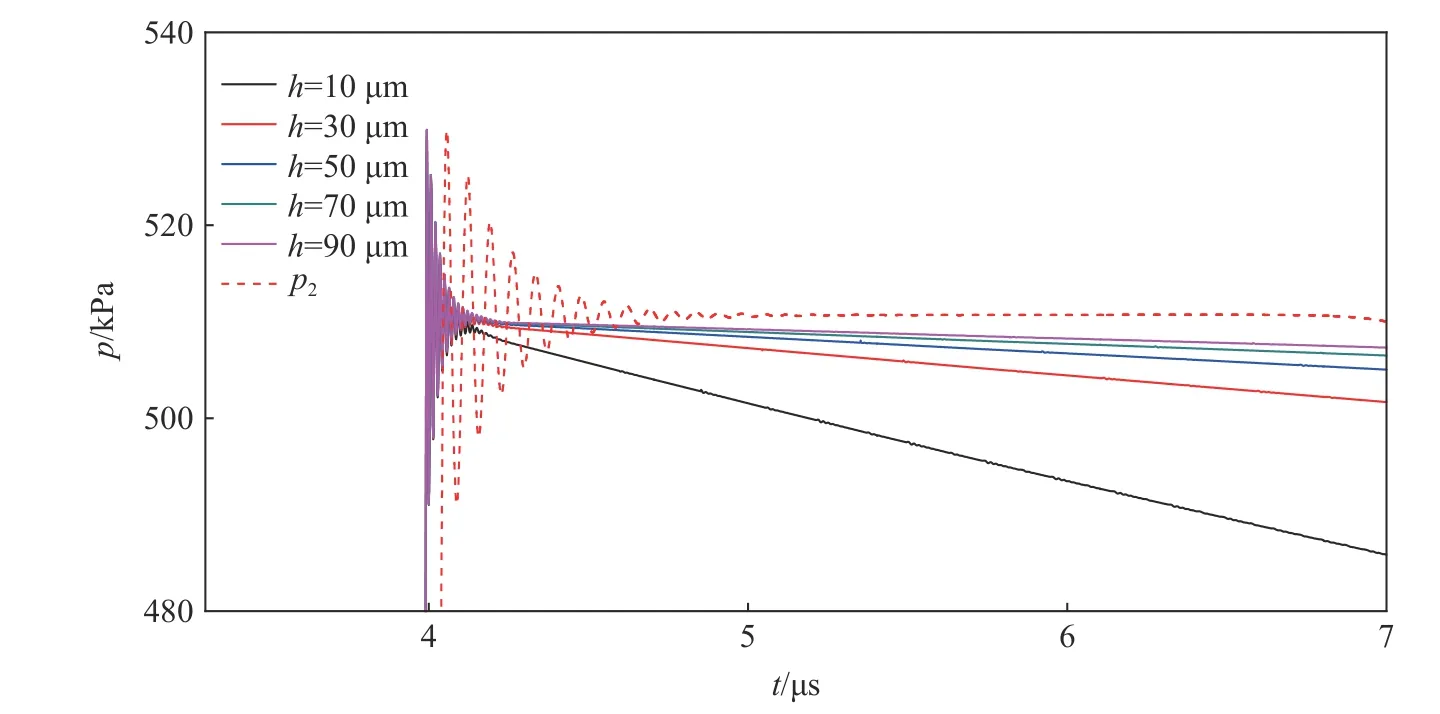
圖4 在0.239 2 MPa 入射壓力作用下不同厚度薄膜的表面壓力Fig.4 Surface pressure of thin diaphragms with different thicknesses under the incident pressure of 0.239 2 MPa

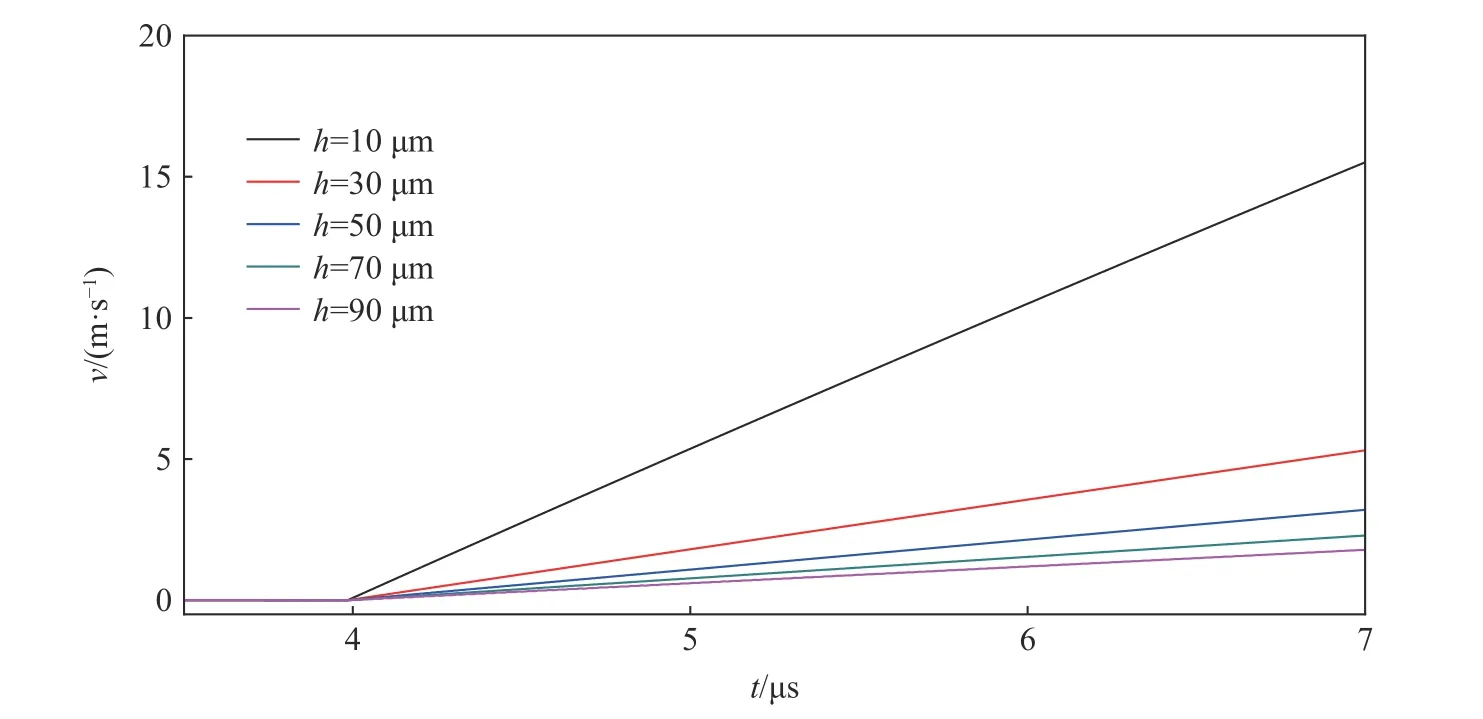
圖5 在0.239 2 MPa 入射壓力作用下不同厚度薄膜的運動速度Fig.5 Velocity-time curves of thin diaphragms with different thicknesses under the incident pressure of 0.239 2 MPa

同樣，可以獲得不同入射壓力作用下，各厚度薄膜的運動速度，以便于開展數據分析。

1.2 爆炸沖擊波加載

化學爆炸、撞擊等過程中產生的沖擊波多數并不是階躍形狀，而是呈現快速上升、指數衰減形狀，有必要開展爆炸沖擊波作用于薄膜的數值模擬，以分析沖擊波壓力下降對測量反射壓力峰值產生的影響。

小當量炸藥近距離爆炸產生的沖擊波具有更陡的下降沿，有利于突出壓力下降對壓力峰值測量的影響。模擬1 g TNT 炸藥爆炸時產生的空氣沖擊波作用于薄膜的情形，建立二維軸對稱有限元模型，選取楔形Euler 網格描述炸藥、空氣和不銹鋼薄膜，網格尺寸均為2.5 μm。空氣半徑為60 mm，對應網格數為24000×1；1 g TNT 炸藥的半徑為5.271 mm，對應網格數量為2108，模型見圖6。某時刻獲得的爆炸沖擊波壓力分布見圖7。

圖6 爆炸沖擊波產生模型Fig.6 Generation model of explosion shock wave

圖7 某時刻爆炸產生的壓力云圖Fig.7 Explosion shock wave pressure distribution at a certain moment

獲取爆心距54 mm 處的沖擊波入射壓力p1，見圖8(a)，峰值為3.294 MPa；與獲得階躍壓力的標準反射壓力類似，在監測入射壓力的網格之后添加足夠多的不銹鋼網格，限制其速度為零，可獲得標準反射壓力p2，見圖8(b)，在壓力最大值對應的時刻之后，取3 個振蕩周期數據的均值為標準值，約為20.10 MPa。

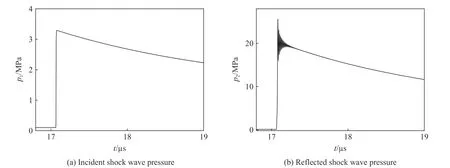
圖8 爆心距54 mm 處的入射沖擊波壓力和反射沖擊波壓力Fig.8 Incident and reflected shock wave pressures at 54 mm away from explosion center

不約束薄膜網格的運動狀態，可獲得不同厚度不銹鋼薄膜在爆炸沖擊波壓力作用下的運動參數歷程，薄膜厚度依次為10、30、50、70 和90 μm，獲得薄膜自由面的運動速度見圖9。類似地，爆心距選取36 mm，可獲得反射超壓峰值為58.55 MPa 的沖擊波，并獲得各厚度薄膜的運動速度，以便于開展數據分析。

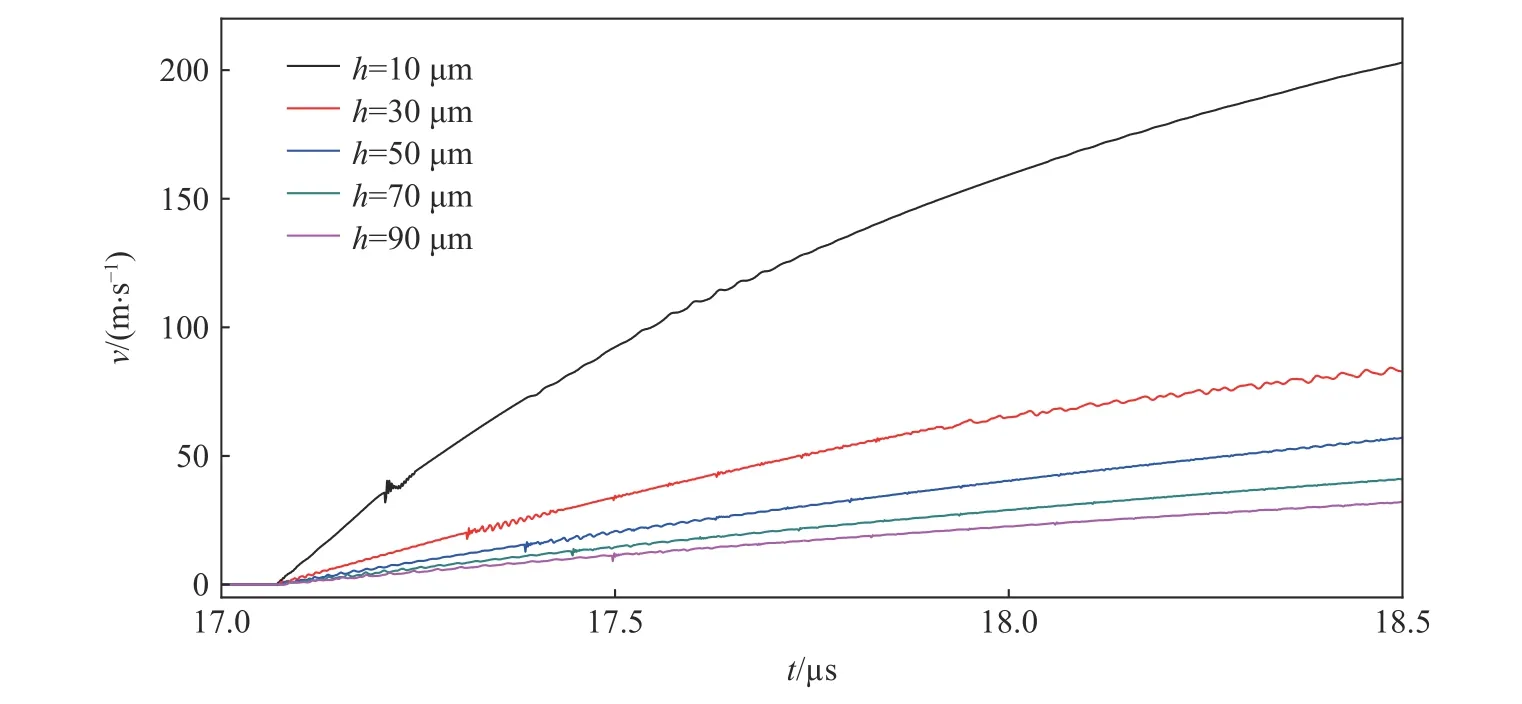
圖9 爆心距54 mm 處不同厚度薄膜的運動速度Fig.9 Movement velocities of thin diaphragms with different thicknesses at 54 mm away from explosion center

2 數據分析

數值模擬可以獲得各個工況下薄膜在沖擊波壓力作用下的運動速度，進一步可獲取加速度，再結合薄膜的面密度數據，可求出作用于薄膜的壓力。將求出的壓力與數值模擬中已知的標準反射壓力相比較，以評估該工況下薄膜式壓力測量的優劣。

在薄膜式壓力測量方法中，利用光纖F-P (Fabry-Pérot)干涉儀獲取薄膜的運動參數，受到干涉測量精度和有效測量時長的影響[12]，需要利用微秒量級的薄膜位移（或速度）數據獲取沖擊起始時刻的加速度，進而估算沖擊波反射壓力峰值。從圖4 可以看出，薄膜受沖擊表面的壓力逐步降低，薄膜厚度越小，下降幅度越大。導致該現象的原因：在沖擊波壓力作用下，薄膜從靜止開始加速，隨著薄膜速度的升高，薄膜對入射壓力的反射效果減弱，導致壓力下降。壓力下降，加速度也下降，若利用薄膜速度數據進行直線擬合求取加速度，相當于求取了擬合時長（擬合數據的時間長度）內加速度數據的平均值，會降低壓力測量精度。因此，提出利用二次及以上多項式來進行速度擬合，再對擬合獲得的多項式進行微分，獲取沖擊起始時刻的加速度，以此來補償壓力下降對測量的影響。

以78.05 MPa 階躍壓力下30 μm 厚不銹鋼薄膜的運動速度曲線為例，開展數值模擬的數據分析。根據速度數據，獲得不同擬合時長、不同擬合階次、不同擬合起始時刻的擬合參數，利用擬合參數估算沖擊波到達時刻的加速度，進而估算出壓力數據，并獲得相對于標準壓力78.05 MPa 的相對誤差，如圖10 所示，其中橫坐標所示的時間表示擬合相對于沖擊波到時的起始時刻，該參數的設置用于反映擬合操作的穩定性，體現在選取擬合數據段時人為因素和部分測量數據缺失情況下獲取加速度的精度；以2d-0.4 μs 擬合參數為例，進行擬合條件說明，該參數表示利用二次多項式對0.4 μs 的數據進行擬合（d 為階次 degree 的首字母）。

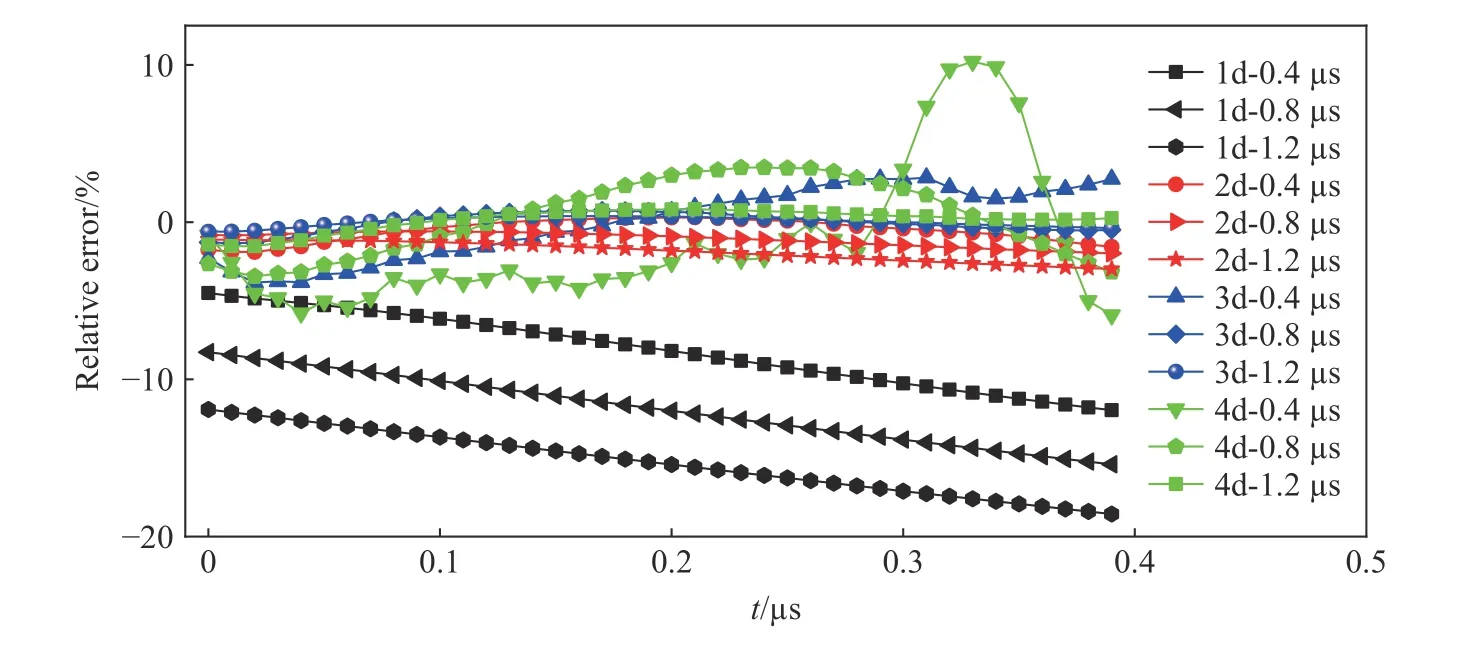
圖10 78.05 MPa 階躍壓力下30 μm 厚薄膜速度數據擬合獲取壓力的相對誤差Fig.10 Relative errors of pressure obtained from the velocity data of 30-μm-thick diaphragms under the step pressure of 78.05 MPa

同樣地，可以對78.05 MPa 階躍壓力下90 μm 厚度不銹鋼薄膜的速度數據進行分析，獲得各條件下的相對誤差，如圖11 所示。因為在4d-0.4 μs 工況下相對誤差過大，超過200%，所以未繪制該工況下的相對誤差。

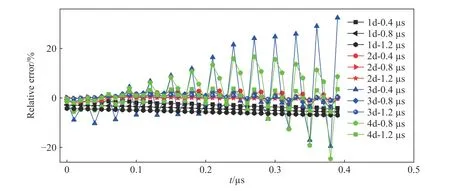
圖11 78.05 MPa 階躍壓力下90 μm 薄膜速度數據擬合獲取壓力的相對誤差Fig.11 Relative errors of pressure obtained from the velocity data of 90-μm-thick diaphragms under the step pressure of 78.05 MPa

為更直觀地展示不同工況下的相對誤差，將78.05 MPa 階躍壓力下不同厚度薄膜速度數據擬合獲取壓力的相對誤差進行匯總，利用誤差帶的方式展示，并除去相對誤差過大的數據，見圖12。類似地，可以獲得4.619 MPa 階躍壓力下，不同厚度薄膜速度數據擬合獲取壓力的相對誤差，見圖13，獲得峰值為20.10 MPa 的爆炸沖擊波作用下不同厚度薄膜速度數據擬合獲取壓力的相對誤差，見圖14。

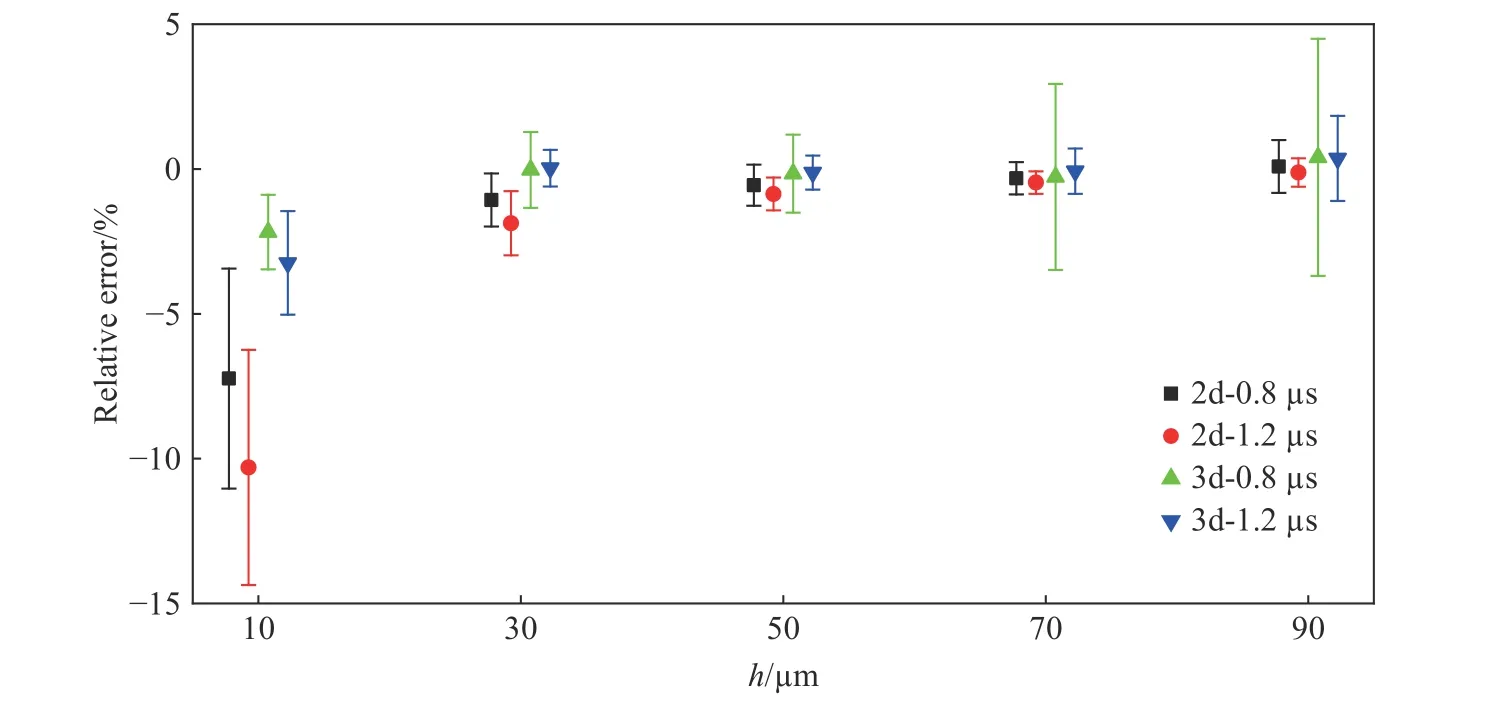
圖12 78.05 MPa 階躍壓力下不同厚度薄膜速度數據擬合獲取壓力的相對誤差Fig.12 Relative errors of pressure obtained from the velocity data of the diaphragms with different thicknesses under the step pressure of 78.05 MPa

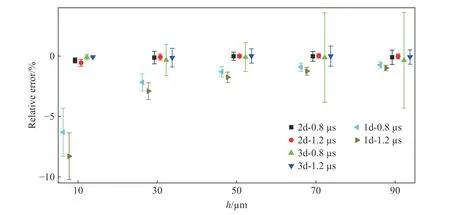
圖13 4.619 MPa 階躍壓力下不同厚度薄膜速度數據擬合獲取壓力的相對誤差Fig.13 Relative errors of pressure obtained from the velocity data of the diaphragms with different thicknesses under the step pressure of 4.619 MPa

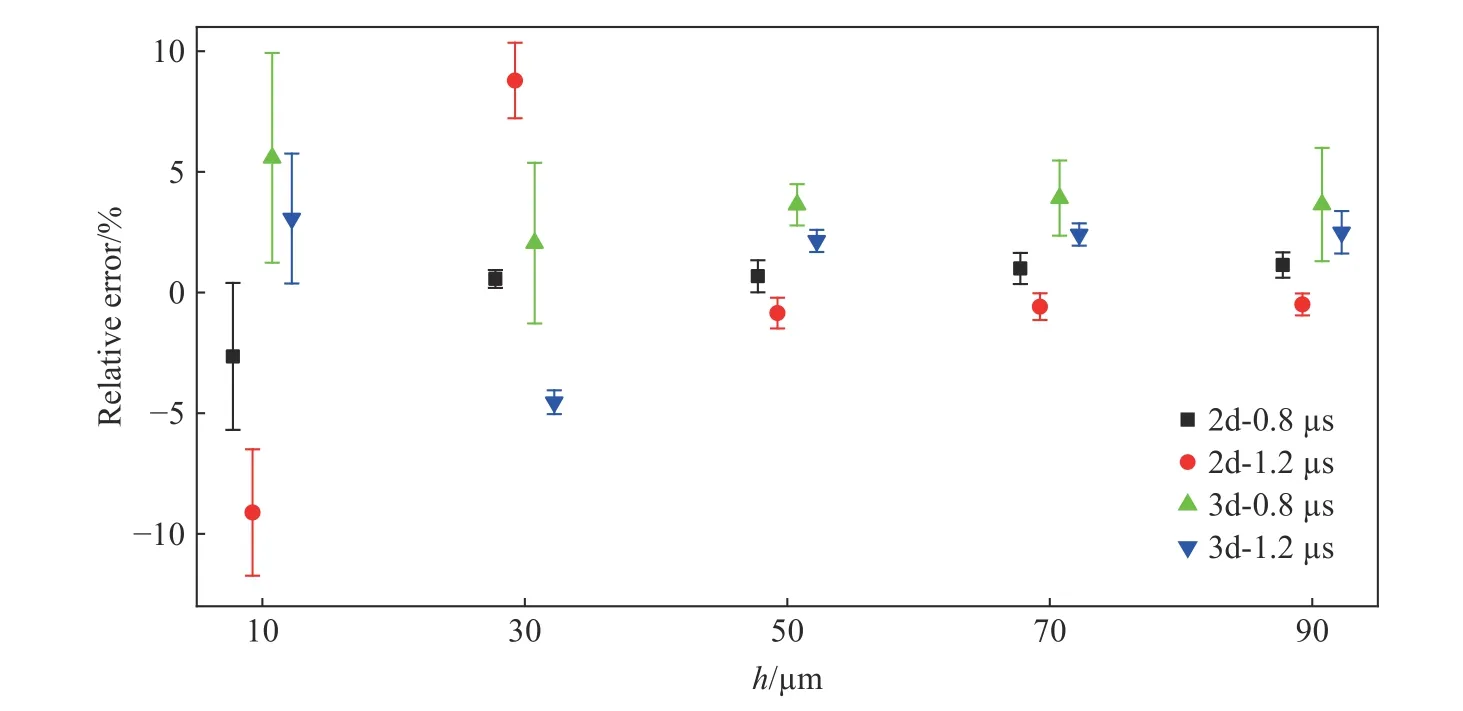
圖14 20.10 MPa 爆炸沖擊波下不同厚度薄膜速度數據擬合獲取壓力的相對誤差Fig.14 Relative errors of pressure obtained from the velocity data of diaphragms with different thicknesses under the shock wave pressure of 20.10 MPa

對速度數據的擬合分析進行歸納，獲得不同待測壓力作用下，不銹鋼薄膜厚度、擬合起始時刻范圍、擬合階次、擬合時長等參數的優選值，以及不同條件下擬合獲得的壓力與標準壓力的相對誤差，見表1。

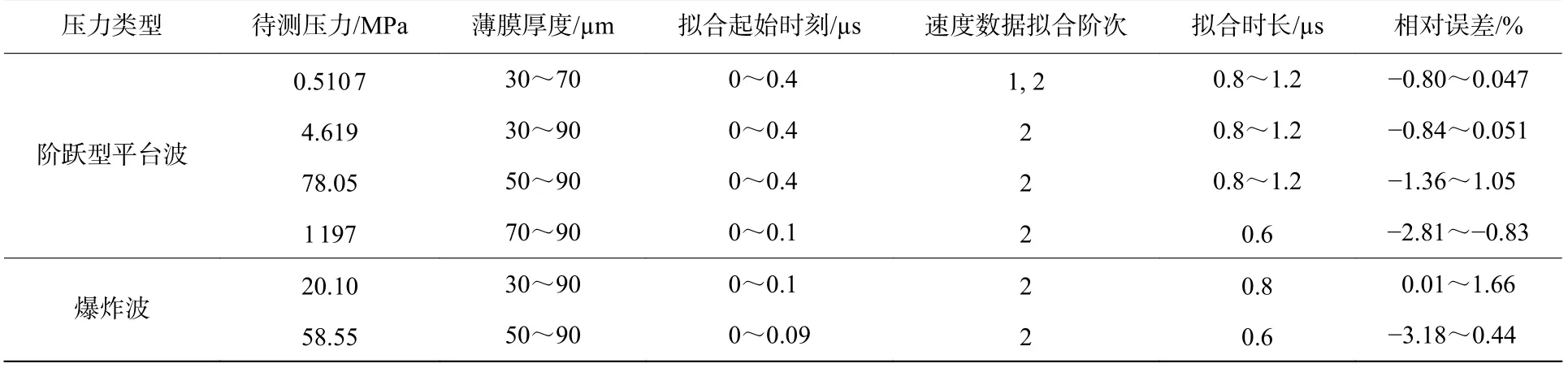
表1 不同待測壓力下擬合參數的優選值及不同條件下擬合獲得的壓力與標準壓力的相對誤差Table 1 Priority values of fitting parameters under different pressures to be measured and relative errors between the fitted pressures and the standard pressures under different conditions

整體上，可得到一些規律，當待測壓力較高或者薄膜厚度較小時，薄膜將在相同時間內獲得更高的運動速度，使得薄膜對入射壓力的反射效果減弱，且空氣阻力增大，由于模型誤差的存在，若利用低階次多項式開展擬合，擬合時長越大，相對誤差越大；相反地，當待測壓力較低或者薄膜厚度較大時，若利用高階次多項式開展擬合，擬合時長越小，則擬合參數的不確定度增大，相對誤差更離散。

獲得薄膜式壓力傳感器敏感薄膜厚度的優選區間為50～70 μm，擬合參數方面：速度數據擬合為二次（待測壓力小于1 MPa 時，選擇一次，有利于測量精度的提高）、擬合時長約0.8 μs。理論上，對于5 MPa（參考表中4.619 MPa 平臺波對應的數據）及以下反射壓力，測量的相對誤差可控制在1%；對于5 MPa～1 GPa 范圍內的反射壓力，測量的相對誤差可控制在3%以內。這在沖擊波壓力測量領域屬于先進水平，薄膜式壓力傳感器具有良好的應用前景。

3 實驗驗證

在激波管底部端面，布置不同厚度的薄膜式光纖壓力傳感器[12]和標準壓阻式壓力傳感器，驗證數據分析章節的部分結論。激波管產生的沖擊波被認為是理想的階躍壓力信號[17-18]，壓力的上升時間可達納秒量級，階躍平臺的持續時間一般超過毫秒量級[19]。實驗中，2 種類型壓力傳感器的響應時間都遠大于激波管壓力的上升時間，因此2 種壓力傳感器的輸出均為階躍響應。

某次實驗中獲得的10 和50 μm 厚薄膜式光纖壓力傳感器原始干涉信號見圖15，獲得的壓阻式壓力傳感器輸出壓力信號見圖16，可見信號存在震蕩和過沖現象，該現象由壓阻式壓力傳感器（其力學模型一般為單自由度二階系統）在階躍壓力作用下產生[17]。為準確求出激波管的平臺壓力，以平穩數據段（200～500 μs）的均值為參考壓力，約0.9460 MPa。

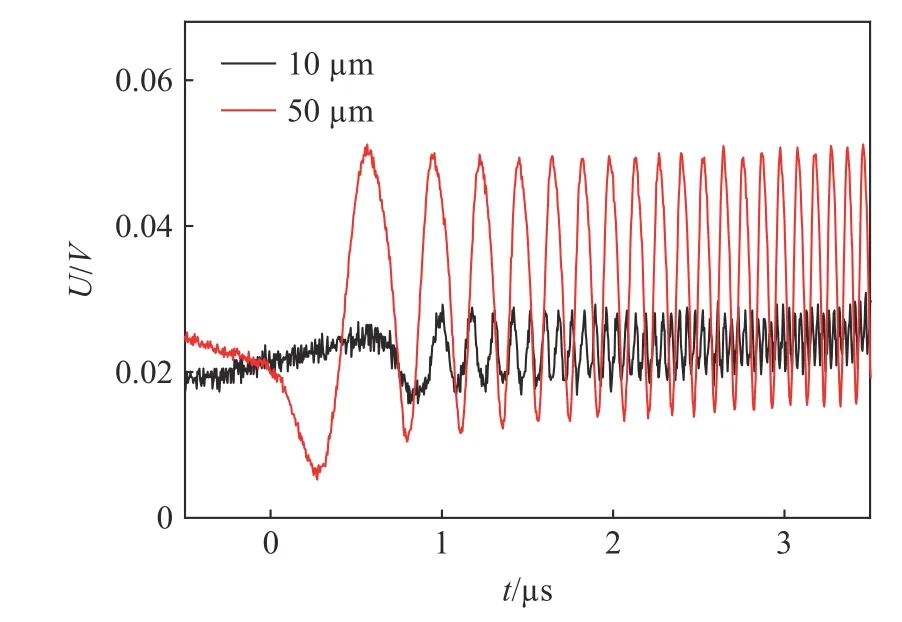
圖15 光纖壓力傳感器的原始信號Fig.15 The original signals of the optical pressure sensors

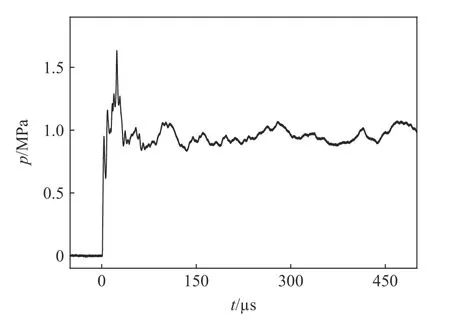
圖16 參考壓力傳感器的數據波形Fig.16 The signal of the reference pressure sensor

利用峰值識別方法獲取光纖干涉信號的峰值，具體步驟包括：(1)對干涉信號進行低通濾波，去除高頻噪聲；(2)求取干涉信號的基線，并利用該基線將濾波后的干涉信號分割為多個區域；(3)求各個區域的極值，獲得干涉信號的系列峰值。根據雙光束干涉的相關理論，由峰值數據可獲得薄膜的位移數據。進一步，開展位移數據的二次多項式擬合（相當于速度數據的直線擬合），見圖17。

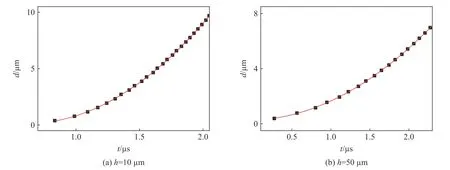
圖17 厚度10 和50 μm 薄膜位移數據的二次擬合Fig.17 Second-order polynomial fitting of displacement data for 10- and 50-μm-thick diaphragms

利用位移數據的二次多項式擬合（相當于速度數據的直線擬合），估算10 和50 μm 厚薄膜的加速度為9.332×106和 2.438×106m/s2，已經測得薄膜面密度為0.09683 和0.37730 kg/m2，根據薄膜式壓力計算公式，可得到對應的反射超壓為0.9037 和0.9198 MPa。已知參考壓力0.9460 MPa，可計算出二次擬合獲取壓力的相對誤差分別為?4.48%和?2.77%。

類似地，開展位移數據的三次多項式擬合，估算10 和50 μm 厚薄膜的加速度分別為9.5957×106和2.4380×106m/s2，對應的壓力分別為0.9292 和0.9199 MPa，相對于參考壓力0.9460 MPa 的相對誤差分別為?1.78%和?2.75%。

薄膜位移數據的二次和三次多項式擬合共獲得4 個壓力值，其中10 μm 薄膜位移數據的二次多項式擬合獲得的壓力值最小，其余3 個擬合獲得的壓力相近，最大相對誤差為1.02%。觀察圖14 可以到同樣的結論，即10 μm 厚薄膜速度數據的直線擬合（相當于位移數據二次擬合）獲得的壓力最小。該現象說明：當薄膜厚度較小時，受到薄膜速度過高導致壓力反射效果下降、空氣阻力增大等因素的影響，位移數據的二次擬合誤差較大，可利用三次擬合或者厚度較大的薄膜來獲取壓力，該結論與數值模擬獲得的結論相符合。

4 結 論

圍繞薄膜式壓力傳感開展了數值模擬，分析了不同厚度薄膜在不同待測壓力下的響應情況，并進行了薄膜式壓力傳感器與標準壓阻式壓力傳感器的激波管比對實驗，主要結論如下。

(1)對數值模擬獲得的薄膜速度數據進行分析，獲得不同擬合時長、不同擬合階次、不同擬合起始時刻條件下，薄膜式壓力傳感器的測量相對誤差。

(2)在薄膜式壓力測量中，入射壓力反射效果減弱和空氣阻力增大，將對壓力測量產生影響，利用薄膜速度數據的二次多項式擬合，可有效降低該影響，提升壓力測量精度。

(3)獲得了薄膜式壓力傳感器的優選參數：不銹鋼薄膜厚度取50 ～70 μm；擬合時長約0.8 μs。理論上，對于常規壓力至極高壓力（吉帕量級）的沖擊波反射超壓峰值測量，相對誤差可以控制在3%以內。