求解含參三次函數問題要有四種意識
周 胥
(廣東省深圳市布吉高級中學)
縱覽歷年高考,三次函數問題的考查力度逐年增大.在高次函數家族里,三次函數雖然最簡單,但當三次函數問題中含有參數或與其他知識綜合考查時,它的難度就上升了,因此很有必要對三次函數問題的求解策略進行研究.筆者認為,求解含參三次函數問題要有四種意識,即方程意識、數形結合意識、分類討論意識和等價轉化意識,本文將依次舉例說明.
1 方程意識
求參數的值,一般采用待定系數法,通過解方程解決.對于含參數的三次函數解析式,要確定參數的值,可以根據題設條件列方程或方程組.
例1已知函數f(x)=2x3+ax2+bx+1的極值點為-1和1,求函數f(x)的解析式.
分析根據導數與極值點的關系列方程或方程組求解得出a,b的值,由此得出解析式.
解易求出f(x)的導數f′(x)=6x2+2ax+b,因為f(x)的極值點為-1和1,所以
點評
本例中的三次函數有兩個待求參數,所以可建立方程組求解.這類問題難度不大,主要考查函數極值的意義.
2 數形結合意識
利用導數知識,很容易作出三次函數的圖像.三次函數的導數是二次函數,它的圖像也容易作出.我們可以利用它們圖像之間的關系找到三次函數問題的解題思路.
例2已知函數有兩個極值點x1,x2,若f(x1)=x1<x2,則關于x的方程[f(x)]2+bf(x)+c=0的不相等的實根個數為( ).
A.2 B.3 C.4 D.5
分析對函數進行求導,將函數的兩個極值點x1,x2轉化為f′(x)=0 的兩個根,即可推出關于f(x)的方程[f(x)]2+bf(x)+c=0 的兩個根為f(x)=x1或x2.若f(x1)=x1<x2,由導函數圖像,判斷函數的單調性,并畫出函數圖像,由圖像即可求出方程[f(x)]2+bf(x)+c=0不同的實根.
解因為f′(x)=x2+bx+c,由題意知x1,x2是函數f(x)的兩個極值點,即x1,x2是方程x2+bx+c=0 的兩個根,從而關于f(x)的方程[f(x)]2+bf(x)+c=0有兩個根,f(x)=x1或x2.
若f(x1)=x1<x2,則根據題意可畫出函數f′(x)和f(x)的圖像,如圖1、圖2所示.
一陣涼風透過窗戶縫隙吹進來,把緊閉著的衛生間窗簾掀開了一條縫。她一驚,伸手要去拉攏來。可就在她的手觸到窗簾的剎那間,她的目光無意間投向了窗外,她看到了一個令人心跳耳熱的鏡頭。對面一間房子的窗戶,窗口的大紅雙喜還未褪色,不知是疏忽,還是過于急切,那對年輕夫妻未拉上窗簾也未關燈就除去彼此的衣物,赤裸地滾落床第,兩具肉體像柔軟的藤條般纏繞在一起,似乎憋足了半個世紀的愛和欲要在這一刻盡情地傾瀉……
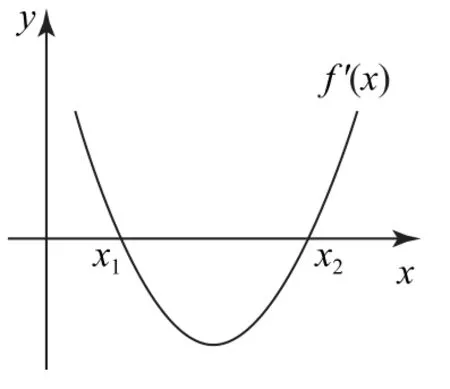
圖1

圖2
由圖可看出f(x)=x1有兩個不相等的實根,f(x)=x2只有一個實根.
綜上,方程[f(x)]2+bf(x)+c=0的不相等的實根個數為3個,故選B.
點評
上面的解法借助數形結合揭示了三次函數圖像及其導函數的圖像之間的關系,解題過程既直觀,又清晰.
3 分類討論意識
當含參數的三次函數問題要求某個參量的取值范圍時,一般需分類討論,尤其是函數單調性與極值的討論,是常考題型.
例3若函數f(x)=(x+2)2(x-a)的極小值小于0,則實數a的取值范圍為_______.
分析根據導數的性質,結合導函數零點的大小關系、極小值的定義分類討論進行求解即可.
點評
根據導函數f′(x)零點的大小進行分類討論是解答本題的關鍵.在許多研究函數性質的問題中,我們常常利用不等式作為解題的工具.求函數的單調區間,對應著解相應的不等式;求參數的取值范圍,對應著研究不等式恒成立問題,于是通常把原問題轉化為含參不等式問題,因此解題時要有分類討論意識.
4 等價轉換意識
求解含參三次函數問題,通常可通過求導將原問題轉化成二次問題(包括二次函數、二次方程和二次不等式),最常見的是方程有解問題和不等式恒成立問題.
例4(1)已知沒有極值,則實數a的取值范圍是( ).
A.(0,1) B.(-∞,0)∪(1,+∞)
C.[0,2] D.(-∞,0]∪[2,+∞)
(2)已知f(x)=x3-x,如果過點(2,m)可作曲線y=f(x)的3條切線,則m的取值范圍是_______.
分析(1)根據導數與函數極值的關系可知f′(x)≥0或f′(x)≤0恒成立,再結合二次函數的性質即可求解本題.(2)由導數法可得過(t,f(t))的切線方程為y=(3t2-1)x-2t3,由過點(2,m)可作曲線y=f(x)的3條切線得m=-2t3+6t2-2有3個不相等的實根,令g(t)=2t3-6t2+2+m,由導數法討論函數的單調性與極值,根據數形結合得出范圍即可.
解(1)因為所以f′(x)=x2+2(a-1)x+1.
因為f(x)沒有極值,所以f′(x)≥0或f′(x)≤0恒成立.又因為f′(x)的開口向上,所以f′(x)≥0恒成立,即Δ≤0,所以[2(a-1)]2-4≤0,整理得a2-2a≤0,解得0≤a≤2,所以a∈[0,2],故選C.
(2)f′(x)=3x2-1,則過(t,f(t))的切線為yf(t)=f′(t)(x-t),即y=(3t2-1)x-2t3.由過點(2,m)可作曲線y=f(x)的 三條切線,得m=-2t3+6t2-2有3個不相等的實根.
令g(t)=2t3-6t2+2+m,則g′(t)=6t2-12t,由g′(t)=0,得t=0或2.
當t<0或t>2,g′(t)>0,g(t)單調遞增;當0<t<2,g′(t)<0,g(t)單調遞減,故當t=0 時,函數g(t)取得極大值2+m;當t=2時,函數g(t)取得極小值m-6.要使g(t)=0 有3 個不相等的實根,則-2<m<6,即m的取值范圍是(-2,6).
點評
第(1)問中的函數f(x)沒有極值,可等價轉化為該函數單調,即f′(x)≥0或f′(x)≤0,于是轉化為不等式恒成立問題;第(2)問中過一定點作出曲線的三條切線很難理解,更不容易正確使用該條件,往往會使思維陷入誤區,但合理地將存在三條切線問題轉化為方程存在3個不相等的實根問題,降低了問題難度,體現了轉化的重要作用.
數學解題,思想方法先行.以上四種意識,也是破解三次函數問題基本的思想方法.
(完)

