一致收斂二元函數列及函數項級數的含參量積分性質

費時龍,任雅柔

(宿州學院 數學與統計學院,安徽 宿州 234000)

數學分析中很多教材研究了含參量積分的連續性、可積性與可微性,給出了累次積分交換次序的條件[1-4]。隨后,函數列、函數項級數及其極限性質及多元函數的性質受到部分學者的關注：費時龍,洪佳音,朱少娟[5]研究了多元函數列的一致收斂性及其相關極限性質;王飛,費時龍[6]討論了多元函數項級數的一致收斂及其性質;王素娟[7]利用幾何的方法,對二元函數可微的定義進行了詳細的描述;趙艷輝[8]研究了積分一致絕對連續的函數列與一致收斂的函數列及一致可積函數列之間的關系。在此基礎上通過二元函數列的性質討論了一致收斂的極限函數及函數項級數和函數的含參量積分的性質,研究了一致收斂的極限函數及函數項級數和函數對應的含參量積分的存在性、連續性、可微性與可積性。獲得了一致收斂意義下極限函數對應的含參量積分與極限交換次序、求導交換次序及累次積分交換次序的條件,得到了一致收斂意義下含參量積分與無窮求和交換次序,含參量積分的求導與無窮求和交換次序的條件。

1 一致收斂二元函數列極限函數的含參量積分性質

定義1.1[5]設fn(x,y)與f(x,y)在集合D?R2上有定義,若對任意給定的正數ε,總存在正整數N,使得當n>N及任意(x,y)∈D時,都有|fn(x,y)-f(x,y)|<ε,則稱二元函數列fn(x,y)在D上一致收斂于函數f(x,y)。

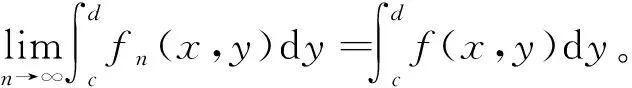
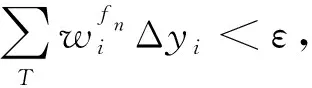
故對上述的分割T：

故對任意的x∈[a,b],f(x,y)在[c,d]上可積,對上述的ε>0,?N>0,s.t.n>N時,有：

即：

注：定理1.2給出了極限函數含參量積分的存在性,得到了極限號與含參量積分交換次序的條件,下面討論極限函數含參量積分的連續性、可微性與可積性。

引理1.3[5](極限函數的連續性)設二元函數列fn(x,y)在二維平面區域D?R2上一致收斂于f(x,y),且對任意n,fn(x,y)在D上連續,則f(x,y)在D上也連續。

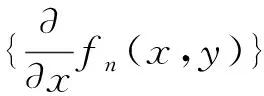
引理1.8[5](極限函數的可積性)設二元函數列fn(x,y)在有界閉域D?R2上一致收斂于f(x,y)且對任意n,fn(x,y)在D上連續,則f(x,y)在D上也可積。

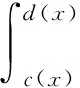
2 一致收斂二元函數項級數和函數的含參量積分性質

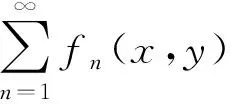
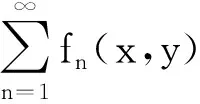
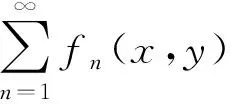
注：定理2.2給出了和函數含參量積分的存在性,得到了無窮求和與含參量積分交換次序的條件,下面討論和函數含參量積分的連續性、可微性。

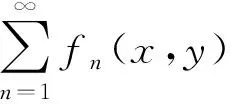
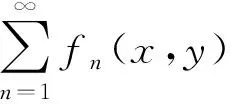
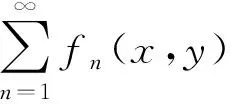
證明由條件及引理1.7顯然。

3 結 論

利用二元函數列的含參量積分性質在一致收斂的條件下分別研究了其極限函數及函數項級數和函數的含參量積分的性質,得到了含參量積分意義下極限與積分交換次序的條件,獲得了極限函數對應的含參量積分的連續性、可微性及可積性。本文的結論和方法可以為多重積分的研究提供新的途徑。