變式訓練教學模式在高中數學解題中的運用
吉林師范大學數學與計算機學院 豐秀悅
變式訓練教學通過對題型的多種變化和靈活的解題方式可顯著提高高中數學教學的趣味性,充分挖掘學生潛能,培養學生發散式思維,從而促進學生對數學知識的多維度理解與運用.因此,為全面提高高中數學學習效率,規避“題海戰術”產生的弊端,應進一步研究高中數學解題環節中變式訓練教學的具體教學策略,以及在不同題型中的應用要點,幫助學生達到事半功倍的學習效果.
1 變式訓練在高中數學解題教學中的應用價值
1.1 提高學生數學學習的效率
在高中數學解題教學中巧妙運用變式訓練有助于提高數學學習的靈活性,從而提升學生在數學課堂的學習效率.在高中數學不同教學階段開展變式訓練教學,首先可為學生營造輕松、高效的數學課堂學習氛圍,幫助學生掌握多種解題技巧與方法.其次,可通過知識的靈活運用節省教學時間,將更多時間留給學生充分思考或探討,增強學生學習數學的主觀能動性.最后,教師亦可借此途徑引導學生對相同知識點所考查的不同題型進行分類總結,促進變式題與母題的融合,為日后的復習打下基礎,提高學生綜合學習能力.
1.2 激發學生的創新思維
當前,社會各行業競爭十分激烈,通過變式訓練培養學生的創新性思維,為國家輸送創新型人才應成為學校教學工作的重中之重.因此,學校要求教師在數學教學中著重鍛煉學生的變式思維.教師首先需具備創新意識,在具體解題過程中充分發揮個人想象力,對題目進行科學分析、合理變式,嘗試利用多種途徑解題,針對不同學生的接受能力展開不同角度的講解,根據學生的反饋對變式方法進行歸納總結,達到多維度激發學生創新思維的效果.此種變式訓練方法具有高效性和新穎性,可幫助學生在短時間內發現解答數學問題的思路,擴寬思考數學問題的廣度,逐漸形成數學教學的良性循環.
2 變式訓練教學在高中數學解題中的運用策略
2.1 類比變式教學策略
類比變式包括解題思路和解題方法的類比,即在某一典型數學問題的解題過程中總結出此類問題的解答思路及方法,運用此種思路同樣可解答與之類似的一類數學問題.教師在設計教學方案時,可以將各階段重要考點分類匯總,選取某一典型例題作為母題,結合該母題采用類比變式,設計出若干變式題目供學生進一步練習,以達到熟練運用該解題思路或方法的目的.
2.2 逆向變式教學策略
高中數學傳統課堂教學中,學生多以正向思維解題,但在長時間的數學學習和大量的習題練習后逐漸形成思維定式,如解題思路單一、解題方法缺少靈活性等.因此,教師在課堂教學中應了解培養學生逆向思維的重要性,通過逆向思維幫助學生從另一個角度理解某個定理、數學概念或知識點.這要求教師在日常教學中為學生設計逆向變式問題,引導學生思考并嘗試解題.例如,代數運算、不等式性質和幾何問題的邏輯推導等方面的題均涉及逆向思維,學生利用逆向思維解決上述問題能提升其推理能力.
2.3 變設問、變條件的教學策略
針對某個數學問題,靈活改變設問方式或命題條件是當前高中數學變式教學最常見的方式,亦是教師在教學初期運用最多的教學方式.鑒于高中數學的整體難度和各學段教學任務,解題教學僅停留在數學問題的表面或只是記憶基本知識點是遠遠不夠的.數學教師應對教材內容進行系統梳理,從多個角度對數學問題展開思考和論證.如,對概念的解析,可針對該知識點設置相應的問題情境,構造同一問題的多種解決方式引導學生深入理解和掌握知識點,進而改變設問方式或問題條件,鍛煉學生“舉一反三”的能力.
3 變式訓練在高中數學教學中的具體運用
3.1 變式訓練在函數問題中的運用
高中數學中變式訓練教學的具體運用,教師可從函數問題開始,將變式訓練融入到函數解題中,引導學生對題目涉及的知識點展開探討,加強對函數知識的分析及應用能力,積累函數解題技巧和經驗,為高中數學函數板塊的學習打下良好基礎.
A.(1,+∞) B.(2,+∞) C.(-∞,2) D.(1,3)
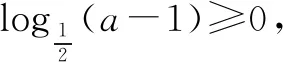
針對該知識點可進一步變換題型,如:
此題與例題1聯系緊密,均考查學生對函數定義域應用的熟練程度,且此題增加了對復合函數增減性的考查.因此,學生首先應求出該函數的定義域,然后根據“同增異減”原則,求得單調遞減區間.經分析可得,該函數定義域為(-∞,1)∪(2,+∞).令t(a)=a2-3a+2,則函數t(a)在(-∞,1)上單調遞減,在(2,+∞)上單調遞增.根據復合函數的同增異減性,最終得到所求的單調遞減區間為(2,+∞).
上述兩道數學題均考查了函數的定義域,而變型題則是對知識點的進一步延伸.此種變式訓練有助于學生對函數知識更加熟練的掌握,同時也有助于增強學生深入思考的能力.
3.2 變式訓練在幾何問題中的運用
幾何問題是高中數學的重點、難點,要求學生具備一定的空間想象力.運用變式訓練教學,可有效降低幾何問題的難度,進而以題目的靈活變換充分鍛煉學生的解題思維.
例2某幾何體的三視圖如圖1所示,試用斜二測畫法畫出它的直觀圖.

圖1
此題考查學生對幾何知識的基本掌握能力.根據給定條件不難畫出幾何體,該幾何體直觀圖如圖2所示.
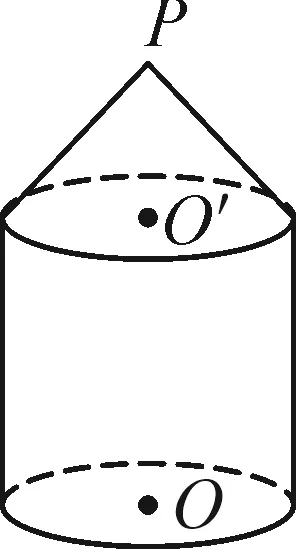
圖2
教師通過該題目帶領學生溫習相關幾何知識,可以此為基礎繼續變式,如:
某幾何體的三視圖如圖3所示,試求其表面積與體積.
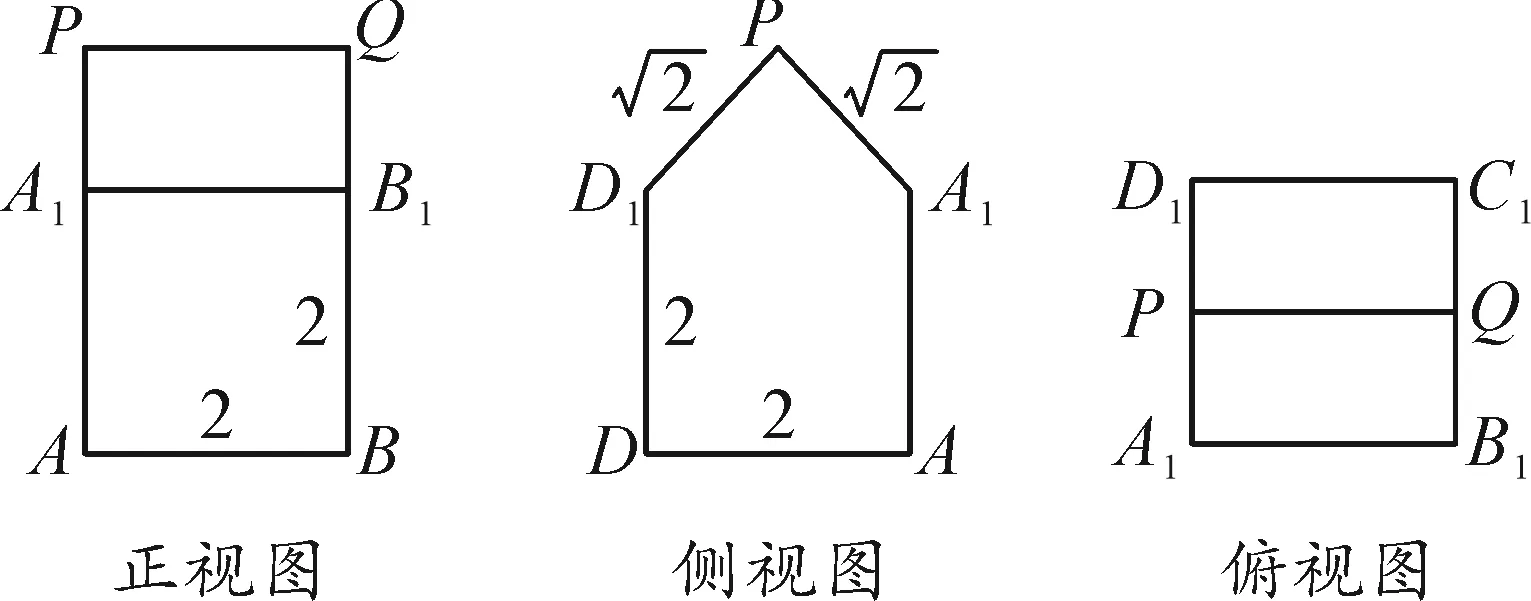
圖3
與例2相比,此題抽象性更強,學生可先在頭腦中構建出該幾何體,然后作答.
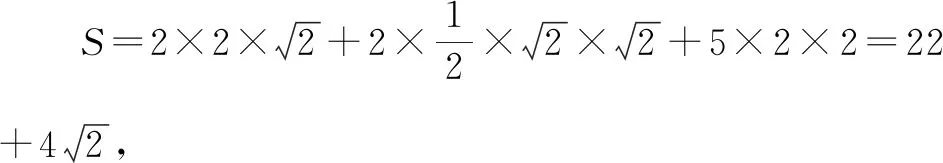
通過以上變式訓練,可幫助學生了解立體幾何問題的變式方法,從而積累幾何問題作答經驗.
將變式訓練應用于高中數學教學中,可有效激發學生的數學思維,減少不必要的練習,更有利于真正落實“雙減”.因此,教師在教學中應注意變式教學方法的使用,充分發揮類比變式、逆向變式以及變設問、變條件等策略的作用,提升學生類比推理能力及歸納總結能力,促使學生掌握多元化的解題方式,增強學生學習數學的信心,全面提升數學素養.

