支持重規劃的戰時保障動態調度研究

曾 斌 樊 旭 李厚樸

作為作戰力量的倍增器,后裝保障系統在現代戰場上扮演著非常重要的角色.它的主要功能是利用有限的保障資源,在最短時間內及時高效地為前線部隊提供急需的作戰物質.在海上分布式殺傷和大規模登陸作戰等戰場背景下,由于遠離本土作戰,前進基地或預置基地保障資源有限,在分布式協同作戰模式下,保障需求點增多,而且保障需求頻率也大幅提高.這種情況下,一個高效的戰時后裝保障系統需要解決的問題包括:

1)當作戰部隊發出保障需求時,如何選擇合適的保障分隊處理該需求;

2)每一個保障基地需要分配多少保障分隊(負責投送作戰物質或維修作戰裝備);

3)當作戰部隊發出保障需求時,如何選擇合適的保障分隊處理該需求;

4)當保障分隊不夠時,如果出現優先級高的保障需求,能否中斷當前保障任務重新規劃;

5)當保障分隊完成任務后,如何根據當前戰場態勢部署至更為優化的地址.

以上問題中,前3 個問題已經有較多研究并得到較好解決,例如,昝翔等[1]和何巖等[2]分別利用遺傳算法解決了維修任務-維修單元的指派,曹繼平等[3]給出了資源沖突時的優化調度方案;曾斌等[4]利用混合Petri 網建立了流程模型并提出了基于退火進化的保障單元調度算法,任帆等[5]指出巡回維修中“預測性”策略要優于“最近修理組”策略,但沒有給出具體的預測算法.

而后2 個問題可以看作前3 個問題的延伸,即在給定一定數量預置保障基地及每個保障基地預分配了一定數量的保障分隊情況下,當出現新的保障申請時,如果當前沒有空閑的保障分隊,如何重分配保障任務及重部署保障分隊.這一直以來也是后裝保障的一個老大難問題,陳春良等[6]在研究展望中專門指出目前關于裝備維修任務調度的研究大多將其視為非搶占調度,易導致維修任務調度不合理、維修資源利用不充分等問題,急需開展搶占調度方向研究.

由于允許搶占拓展了解空間,所以需要尋優,而常規方法難以優化裝備的搶占調度及重規劃,因此需要從智能化保障技術入手,只有能夠對后裝保障與配屬情況進行合理性預測,才能制定魯棒性強的保障計劃與投送方案[7],從而能夠根據戰場環境變化,預見性地做出重規劃決策.

作為預測決策的關鍵技術之一,以馬爾科夫決策過程(Markov decision process,MDP)為基礎結構的強化學習逐漸在智能化應急服務中得到了應用并取得顯著成果[8-9],包括: 救護車的調度[10]、醫療資源的分配[11-12]、災后救援優化策略[13-14]、戰場傷員的疏散方案[15]以及應急電力系統的自適應控制[16-17]等,這些研究給予本文以智能決策技術上的啟發,但同樣也沒有解決重規劃問題.

本文的思路如下: 首先建立戰時保障動態調度問題的MDP 模型;其次提出了該MDP 模型的求解方法.基于強化學習的試探-獎勵-修正(策略迭代)自學習方式,生成不同保障需求事件下的狀態-動作序列,以此作為樣本數據來訓練保障調度神經網絡模型.這樣在實戰過程中,當戰場環境發生變化引發新的保障需求時,不同的保障決策動作將導致系統狀態發生改變,通過訓練好的保障調度神經網絡可以快速計算改變后狀態的價值,其中導致狀態價值最大的決策即為最優決策.

本文主要貢獻包括:

1)定義了支持重規劃的后裝保障動態調度問題,建立了支持重規劃(搶占調度、重分配及重部署)決策的MDP 模型和求解算法;

2)在重規劃MDP 模型中綜合考量了任務排隊、保障優先級以及油料約束等問題的影響;

3)為了解決重規劃MDP 模型狀態動作空間過大引起的“維度災”問題,借鑒了深度學習思想[18],提出利用神經網絡對基函數進行非線性組合,從而逼近MDP 值函數,降低了計算復雜度;

4)采用決策后狀態思想[19]降低了隨機事件引起的計算復雜度.

1 馬爾科夫決策模型

1.1 狀態空間

MDP 的狀態設計非常重要,如果維度過大會影響求解算法的收斂,過小則可能不足以用來描述系統的決策函數、狀態轉移函數以及獎勵函數.本文設計保障系統的狀態S(t,e,M,R),其中,t為當前時間,e表示當前事件類型,M為列表類型,表示各個保障分隊的所處狀態,R為列表類型,表示當前待處理的各個保障需求的狀況.

1.1.1 事件類型

系統狀態隨著事件的產生而變化,為此本文定義7 種事件類型,即e(S)1,2,···,7}.e(S)1表示產生了保障需求需要處理;e(S)2 表示保障分隊到達保障倉庫 (如果保障倉庫與保障分隊處于同一保障基地,則不用產生此事件);e(S)3 表示保障分隊在保障倉庫領取到本次任務需要的物質或備品備件;e(S)4表示保障分隊到達需求點;e(S)5表示保障分隊完成當前保障任務;e(S)6 表示保障分隊返回保障基地;e(S)7 表示有保障分隊處于待命狀態.

1.1.2 保障分隊狀態

保障分隊狀態列表表示為:M[Mm]m∈M′[M1,M2,···],其中,M′{1,2,···},表示系統中所有保障分隊集合,列表中每個組成元素都為一個數組,可表示為

1.1.3 保障需求狀態

保障需求狀態列表可表示為:R[Rr]r∈R′[R1,R2,···],其中,R′{1,2,···},表示保障需求隊列中待處理的所有保障需求集合,列表中每個組成元素都為一個數組,可表示為

如果當前沒有保障需求,Rr(0,0,0,0,0);如果某個保障需求已被完成,則該需求將會移出隊列.另外保障隊列中等待的需求有一個最大閾值rmax|R′|,它表示保障系統能夠支持的保障需求最大數量.

以上狀態相對獨立,可以假設其滿足馬爾科夫過程無后效性性質.其中時間狀態即指當前的時刻,因為較簡單,可以忽略.

1.2 決策空間

1.2.1 決策變量

為了描述決策空間,首先定義如下集合.

1)B{1,2,···,|B|}表示保障基地集合;

2)Q(S){r:′,0}表示當系統狀態為S時,在隊列中等待分派保障分隊處理的保障需求集合;

3)A1(S){m:′,1,6,7,8}}表示當系統狀態為S時,可以分派執行保障任務的保障分隊集合;

4)A2(S){m:′,2,3}}表示當系統狀態為S時,可以重規劃保障任務的保障分隊集合;

5)A3(S){m:′,6}表示當系統狀態為S時,可以重部署的保障分隊集合.

本文中決策變量設計為3 個布爾變量,定義如下:

1)Xmr1表示第m支保障分隊被分派執行保障需求r,否則為0;

2)Ymr1表示第m支保障分隊被命令中斷當前保障任務,重規劃執行新的保障任務r,否則為0;

3)Zmb1表示第m支保障分隊被重部署至保障基地b,否則為0.

1.2.2 決策約束

決策約束分以下4 種情況討論.

情況 1.當Q(S)?(存在待處理保障需求) 且發生事件類型為e(S)1,2,3,4,6,7}時,保障指揮人員需要執行2 個決策: 分派任務和重規劃任務.其中,分派任務負責分派哪一個保障分隊執行隊列中等待處理的保障任務;當沒有可用保障分隊且出現高優先級任務時,由重規劃任務決定中斷哪一個保障分隊的當前任務,轉去執行新的保障任務.

這種情況下存在如下5 種決策約束:

1)約束一個任務只需要一支分隊處理,如果需要多支分隊處理一個任務,可以組合成一個分隊,或放松此約束,即

2)約束一支保障分隊一次只能分派執行一個保障任務,如果需要一支分隊一次執行多個保障任務時,可以把一個保障分隊分解為多支分隊,或放松此約束,即

3)約束一支保障分隊一次只能重規劃執行一個保障任務,即

4)約束保障分隊一次只能分派執行或重規劃執行剩余油料距離之內的保障任務,設dmr表示保障支隊m與需求點r之間的距離,即

設分派調度決策列表為

設重規劃決策列表為

情況1 下的決策空間表述為

情況 2.當Q(S)?(不存在待處理保障需求)且發生事件類型為e(S)5 (有保障分隊完成當前保障任務) 時,保障指揮人員需要決策保障分隊m的重部署地點.注意此時A3(S){m}.設dmb為保障分隊m到基地b的距離,Imb為指示函數,如果保障分隊m剩余油料可以到達某基地b,則為1,否則為0,其表達式為

因此,有決策約束式為

該約束表示每一個保障分隊只能部署到一個保障基地.設該情況下重部署決策列表為

情況2 下的決策空間表述為

情況 3.當Q(S)?(存在待處理保障需求) 且發生事件類型為e(S)5 (有保障分隊完成當前保障任務) 時,保障指揮人員可以選擇以下3 種決策:

1)分派任務: 分派哪一個保障分隊執行隊列中等待處理的保障任務;

2)重規劃任務: 中斷哪一個保障分隊的當前任務,重安排其執行新的保障任務;

3)重部署保障分隊: 如果保障分隊m沒有分派執行隊列中等待處理的保障需求,重部署m到哪一個基地.

注意此時有A3(S){m}.約束表示為

約束(7)表示如果存在可重部署的保障分隊,且其沒有分派執行隊列中的保障需求,則只能將它重部署到最多一個保障基地.此時決策空間表示為

情況 4.如果沒有出現以上事件,也沒有發生以上3 種情況,則約束空間D4?.

1.3 狀態轉移

設第k個事件發生時保障系統所處狀態為Sk,保障系統通過決策動作dk使得系統狀態從Sk演進到Sk+1,并設隨機元素W(Sk,dk)表示系統處于Sk+1時發生的隨機事件信息,整個保障系統的演進動力模型可以表示為

式中,ST表示狀態遷移函數.

1.4 獎勵函數

按照MDP 模型,當有保障分隊調度 (分派或重規劃) 執行保障任務時,該決策行為將會獲得獎勵.獎勵值的設計也是影響強化學習能力的重要因素,本文保障系統中需求優先級、期望保障時間以及需求產生時刻等因素都會影響決策動作的獎勵值.設C(Sk,dk)表示在系統處于狀態Sk時,如果采取決策dk將會獲得的立即獎勵值,它的計算式設計為

1.5 目標函數及優化方程

基于給定策略π(一系列決策的組合),Dπ(Sk)(Sk)為從狀態空間到決策空間的決策函數,用以指導在狀態Sk下采取策略dk.MDP 模型的目的也就是從所有可行策略中計算得到優化策略π*,從而最大化系統的長遠回報.因此,系統目標函數為

式中,γ為一個固定的折扣因子,為了便于計算,Bellman 優化方程利用迭代方式計算目標函數,其表達式為

式中,V(Sk)為狀態Sk的值函數.

2 求解算法

由于維度災(式(11)的狀態空間維度過大)的影響,利用常規動態規劃方法無法取得式(11)的精確解.為此,本文采用近似動態規劃[20]的方法逼近式(11)的值函數.

2.1 隨機事件的計算

另外,式(11)中還需要對期望值E[V(Sk+1)|Sk,dk]求極值,不僅計算量巨大而且會帶來較大的統計誤差,為此本文采用決策后狀態思想[21-22],將先求期望值后求極值問題轉換為先求極值后求期望值問題,從而降低了計算量和誤差.該思想在前后兩個狀態之間 (Sk和Sk+1) 引入了一個中間狀態,即決策后狀態該狀態在決策發生后事件發生前出現,屬于確定性狀態,因此,原來式(8)的一步狀態轉移轉換為兩步,即

其中,ST,x為確定性函數,ST,x和ST,w組合后與式(8)的ST等價.設決策后狀態的價值為

將式(12)代入式(11),優化方程修改為

下面進一步討論式(13)決策后狀態價值的計算,由于式(12)為迭代過程,可以有

式(13)代入式(14)右邊,引入決策后狀態價值的優化方程可表示為

2.2 基函數的設計

盡管式(15)通過引入決策后狀態變量減小了隨機事件帶來的計算復雜性和統計誤差,但是對于式(15)而言,復雜的狀態空間導致的維度災問題仍然存在.為此,本文通過構造基函數捕捉決策后狀態的特征,再以基函數為基礎來設計近似函數以便逼近式(15)表示的價值函數.這里基函數的設計尤為重要[23-24],關系到最后近似價值函數的求解質量.為此本文設計了6 種基函數,通過它們的非線性組合(參見第2.3 節的神經網絡)來表示價值函數.設φf()表示基函數,f為基函數特征,f.

1)第1 種基函數直接表示保障分隊狀態,數量為|M′|,計算式為

2)第2 種基函數捕捉保障分隊執行保障任務(服務-客戶對)的期望服務時間,數量為|M′|.設Imr為指示函數,如果保障分隊m當前執行的保障任務為r,則為1,否則為0,計算式為

3)第3 種基函數捕捉保障分隊執行保障任務的優先級,數量為|M′|,計算式為

4)第4 種基函數捕捉當前在隊列中等待處理的保障需求優先級,數量為|R′|,計算式為

5)第5 種基函數捕捉每一個需求在系統中的逗留時間,數量為|R′|,計算式為

6)第6 種基函數捕捉每一個保障分隊與保障申請點的距離,數量為|M′|×|R′|,該基函數結合保障分隊的狀態可以知道哪一個保障分隊有足夠油料分派或重規劃到某需求點,其計算式為

2.3 神經網絡的設計

由于保障系統狀態空間和決策空間較為復雜,常規線性基函數組合的效果將會因此受到較大影響.所以本文以基函數的輸出結果作為神經網絡輸入,即利用神經網絡對基函數進行非線性組合[25],從而達到逼近式(15)值函數的目的.

為了使學習后的神經網絡能夠近似表達值函數,本文設計了3 層神經網絡結構: 輸入層、隱藏層和輸出層.如圖1 所示,輸入層包含|F| 個輸入,它的值為基函數的輸出,如圖1 中?1,1表示第1 類基函數的第1 個函數輸出值,輸入節點個數為6 類基函數的總個數,輸入層沒有激活單元.為了減小基函數評估值的波動,幫助神經網絡反向傳播算法能夠快速找到權重矩陣,在輸入到輸入層之前,本文對基函數評估值進行了均值歸一化.

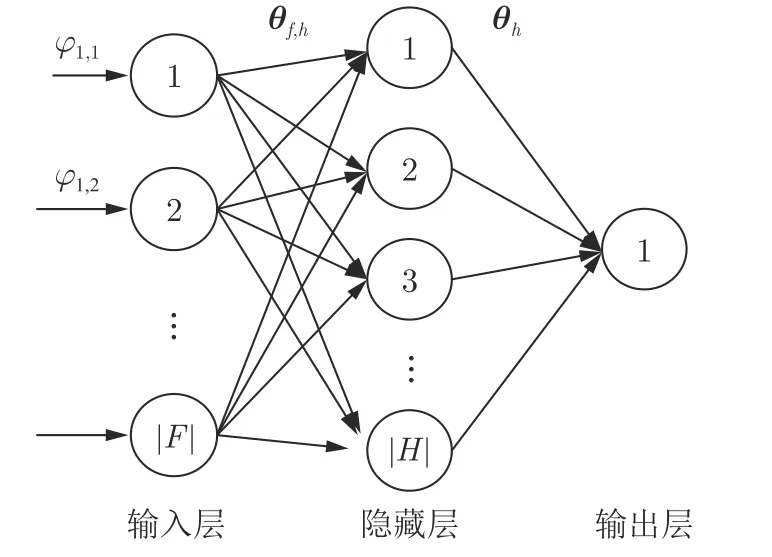
圖1 神經網絡結構示例Fig.1 Illustration of neural network structure

隱藏層包括H{1,2,···,|H|}個神經元,其個數|H| 為超參數,所以隱藏層的輸入表達式為

式中,Ih表示隱藏層中第h個神經元的輸入,θf,h為|F|×|H| 的權重矩陣,控制輸入層到隱藏層的映射關系,隱藏層神經元的激活函數為sigmoid 函數,表示為

因此,隱藏層的輸出表達式為

其中,Oh為第h個神經元的輸出,|H| 個隱藏層神經元輸出與輸出層權重組合生成輸出層的輸入,其表達式為

式中,θh為|H|×1 的權重矩陣,控制隱藏層到輸出層的映射關系,輸出層只有一個神經元,激活函數與隱藏層的相同,也為sigmoid 函數,其表達式為

式中,θ(θf,h,θh) 為神經網絡中需要學習的權重參數.

2.4 神經網絡權重學習算法的設計

本文設計了基于強化學習策略迭代[26]的神經網絡學習算法,如圖2 所示,算法分為2 層循環,第1 層循環(內層循環)為策略評估,利用給定策略(上一次循環更新的神經網絡),在模擬產生的事件驅動下,生成動態演進的狀態價值并作為樣本點保存;第2 層循環(外層循環)為策略改進,利用內層循環保存的樣本點改進神經網絡的權重矩陣.

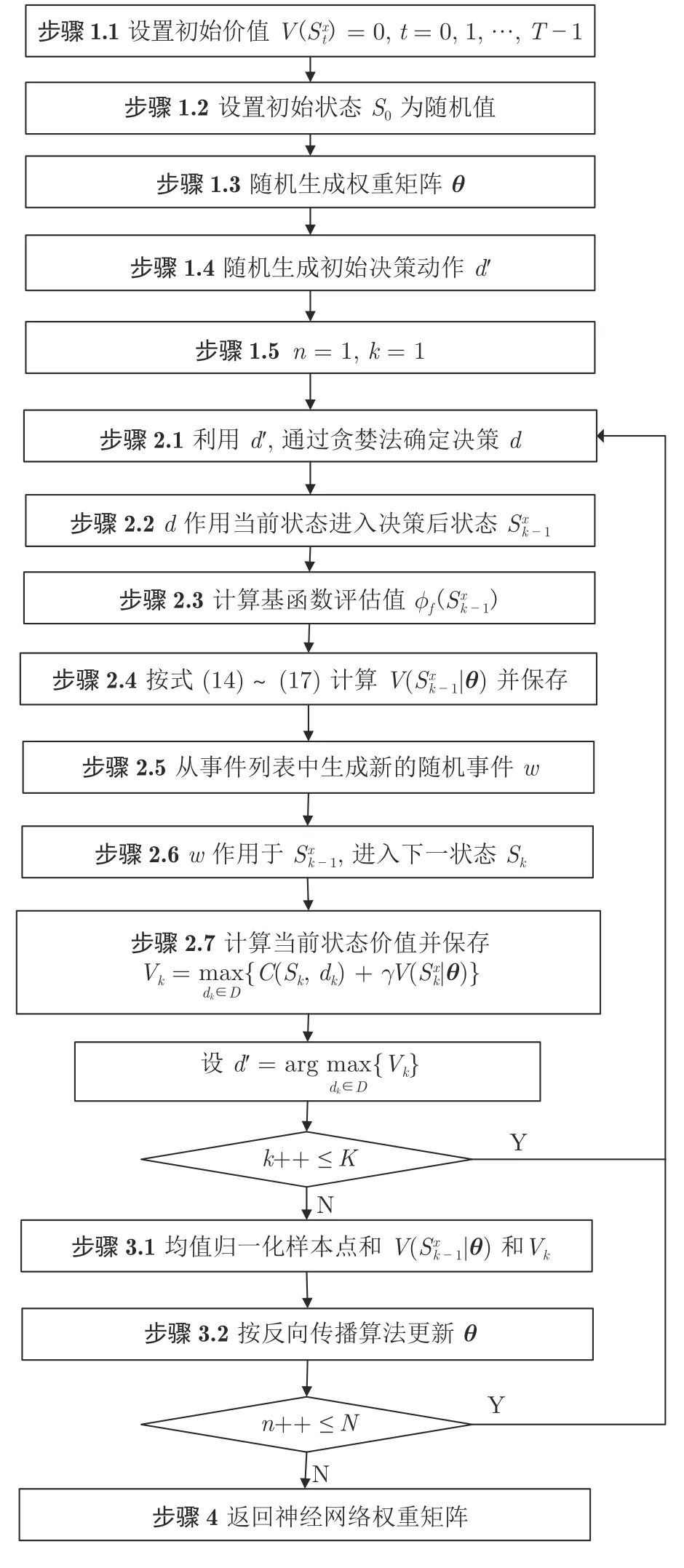
圖2 策略迭代算法流程Fig.2 Workflow of policy iteration algorithm

策略迭代算法外循環每次進行策略改進時都需要調用神經網絡反向傳播算法對權重參數進行訓練,為了防止出現過擬合和泛化誤差,本文在神經網絡代價函數中加入了懲罰項,即

其中,K個樣本點中,在步驟2.4 中存儲,為神經網絡估算值;Vk在步驟2.7 中存儲,為標簽值;正則化參數η用于平衡模型復雜度和邊際誤差.本文采用了自適應預估方法來計算合適的η值,計算式為

式中,v為樣本數據的均值,σv為樣本數據的標準差.

需要計算得到θ*值,使得代價函數最小,即θ*argmin{L(θ)}.為了提高計算速度,本文采用擬牛頓法求解,擬牛頓法需要的梯度信息可以利用神經網絡的反向傳播算法計算得到.

為了平滑θ權重矩陣,本文采用式(20) 來更新θ:

其中,an1/nβ,β(0.3,1],an的下標值n與策略改進外循環次數n一致,通過an控制θ值,在歷史值 (θ)與新估計值 (θ*) 之間取得平衡.隨著策略改進迭代次數n的增加,本算法越來越偏重于過去n-1 次迭代得到的歷史值.

在策略迭代算法的每一次外循環 (策略改進)中,都會按式(18)對神經網絡的權重進行更新,如果n＜N,則算法開始下一輪循環.算法中可調節參數包括N、K、|H|、η和β,其中,N為策略改進的迭代次數,K為策略評估的迭代次數,|H| 為隱藏層節點的個數,η是樣本估計的正則化項,β是步長參數.

2.5 調度算法的使用時機及步驟

建立的神經網絡模型可以看作一個具有預測能力的調度機.其使用時機為: 當戰場態勢變化,例如出現新的保障申請,如第1.1 節描述的當前系統狀態隨之改變.使用步驟如下:

1)在第1.2.2 節描述的決策約束下,生成各種可能的決策動作;

2) 按第1.3 節狀態轉移矩陣,基于當前狀態,采取步驟1)生成的各種可能的決策動作,形成下一步狀態集合S;

3)將下一步狀態集合中的每一個狀態作為第2.2 節敘述的基函數輸入,基函數的輸出為第1 階段的線性預測值,用于降低計算復雜性;

4)為了具有非線性預測能力,如圖1 所示,基函數的輸出作為神經網絡模型的輸入,此時神經網絡的輸出為下一步狀態的價值V(S),該價值為第2.4 節Bellman 方程迭代計算的 “期望” 價值;

5)當狀態集合S中的每一個狀態都經過步驟3)和步驟4),計算出相應期望價值后(該過程可以并行執行),導致下一步狀態價值最大的決策可看作當前最優決策.

3 實驗驗證

本節通過一個分布式戰場保障場景來驗證動態調度算法的適用性.由于MDP 求解算法超參數較多,通過實驗設計測試了不同參數設置對動態算法的影響,并比較了動態算法與兩個比對策略的性能差異.

3.1 實驗參數設置

本文以圖3 所示的一個典型的分布式作戰行動為背景,當交戰區域中我方部隊發出保障申請后,使用上文提出的數學模型及逼近算法計算調度結果,即決定是否接受該申請,如果接受該申請,分派哪一支分隊處理.出于安全考慮,刪除了圖3 的背景地圖,圖3 中有2 個保障基地和2 個前進基地,與保障基地相比,前進基地較小,當沒有申請所需物資裝備時,需要從保障基地補充.圖3 中還包括54 個交戰地點,即保障申請點,分屬12 個區域,由其發出保障申請.

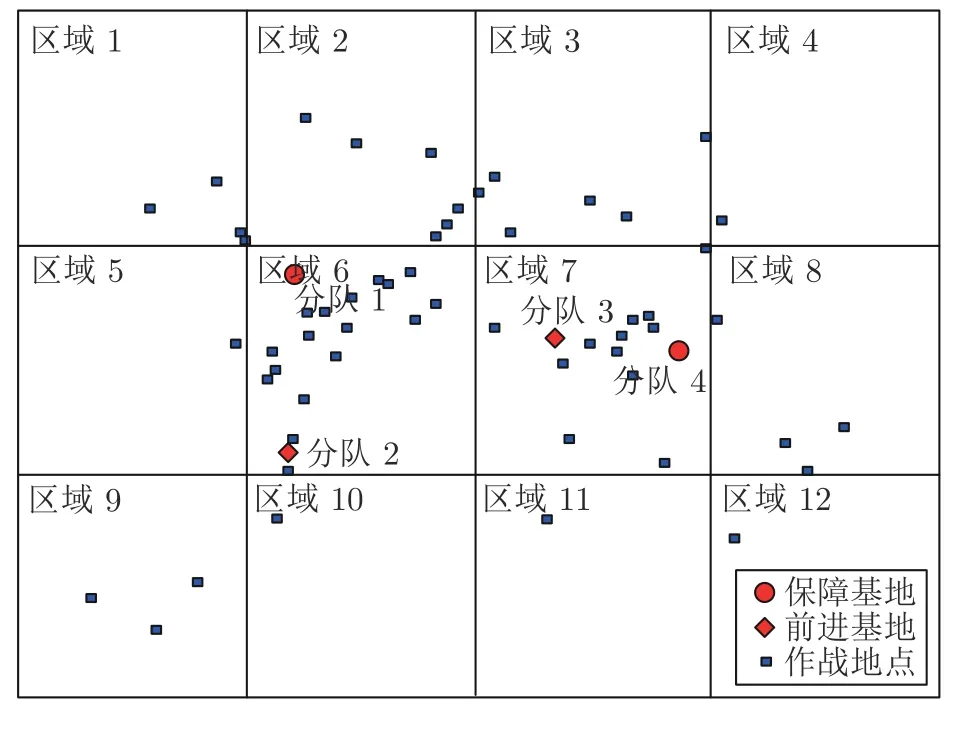
圖3 實驗案例Fig.3 Experiment case

本文使用泊松分布生成保障需求的產生概率,為了能夠接近實戰背景,泊松分布的到達率參數由式(21)生成,即

式中,λ為保障申請發生率;pz為條件概率,表示當發生保障申請時,該申請是從交戰區域z發出的概率;pkz為條件概率,表示當出現保障申請且該申請從交戰區域z發出時,該申請優先級為k的概率.實驗中保障申請發生率λ設為1/45,即平均每隔45 min發出一個保障申請,請求保障分隊執行任務.為了集中反映系統的調度能力,條件概率pkz中緊急保障和一般保障的比例為0.8和0.2.式(9)中緊急保障的優先級權重為0.9,一般保障的權重為0.1,式(10)中折扣因子γ在實驗中設為0.99,該設置使得系統重視未來事件的影響.

為了檢驗動態算法的性能,實驗設計了2 個比對策略.比對策略A 采用常規的最近分配原則,該策略認為當前沒有執行任務的保障分隊為可用資源,當出現保障申請時,分配離該申請點(交戰區域)最近的可用分隊執行此項保障任務,比對策略A 不具備搶占調度能力.比對策略B 將比對策略A 進行了擴展,當出現優先級更高的保障申請時,允許其搶占其他保障分隊當前執行的低優先級任務.兩個比對策略使用的都是最近分配原則,該原則實際上只考慮當前的立即獎勵進行決策(與式(9)相似),沒有用到預測的未來信息(式(10)).另外,由于立即獎勵沒有考慮重部署決策,所以這兩個比對策略都不具備重部署能力.

3.2 超參數調整

本文采用了全因子實驗設計來檢驗不同的超參數對算法性能的影響,主要超參數設置如下: 策略改進迭代次數N{1,2,···,40},策略評估迭代次數K{500,1 000,2 000,4 000},步長參數β{0.3,0.5,0.7,0.9},隱藏層節點數|H|7,正則化項η采用自適應預估方法計算.為了能夠得到合理的置信度,每一個組合運行100 遍仿真,每次仿真時長為1 000 min 以上.仿真實驗結果如表1 所示,其中,性能相對改進量計算式為

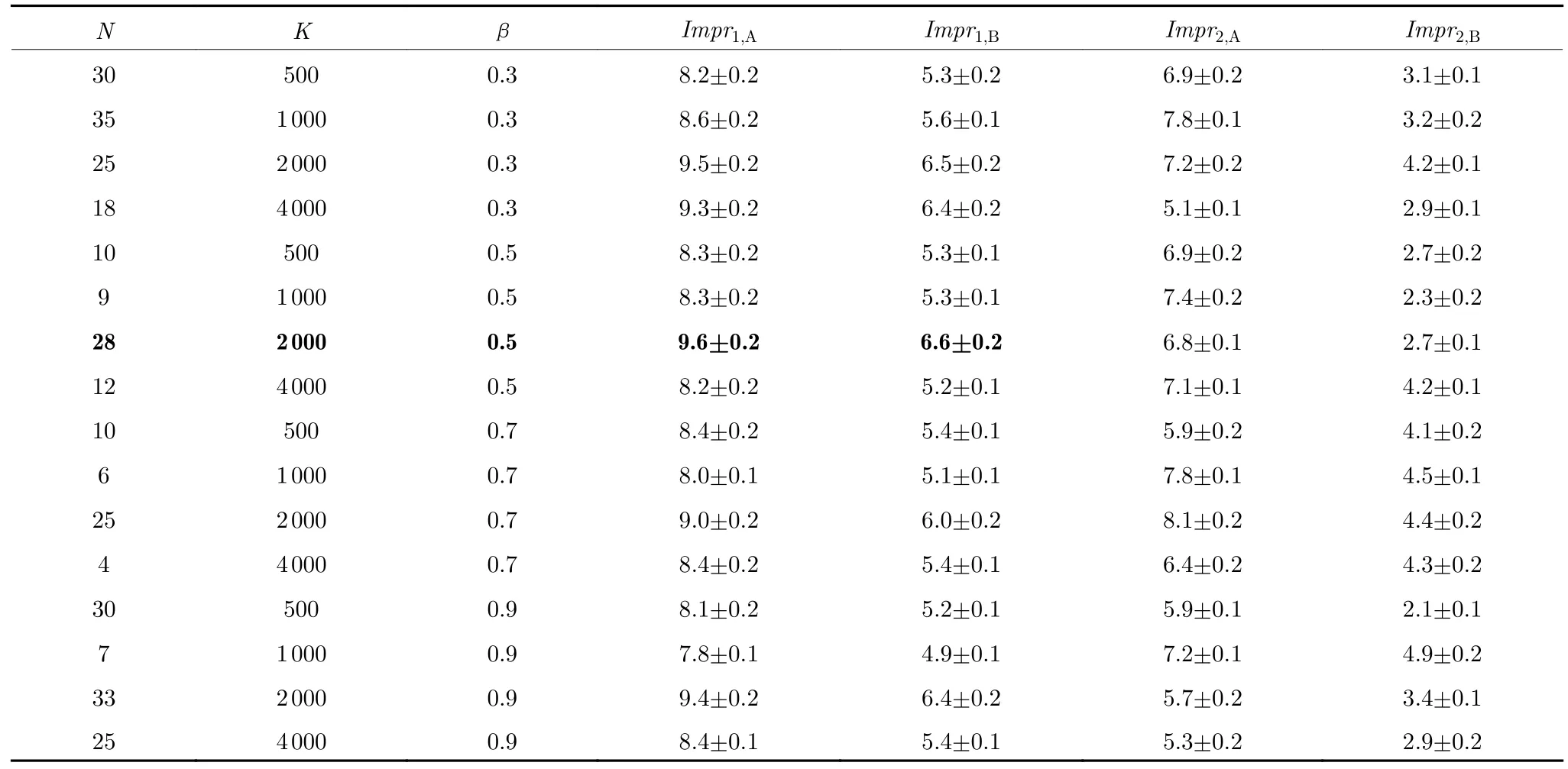
表1 仿真實驗結果Table 1 Simulation results

其中,Vi為采用i算法計算得到的價值,Vj為采用j算法計算得到的價值,表1 中Impr1,A和Impr1,B分別為本文基于神經網絡的動態算法相較于比對策略A和策略B 得到的性能相對改進量.

另外,為了考量神經網絡模型的性能,設計了基函數的線性回歸模型作為比較算法,Impr2,A和Impr2,B分別為線性回歸模型相較于比對策略A和策略B 得到的性能相對改進量.表1 中仿真結果數據的置信度都為95%.

表1 中左邊3 列為仿真實驗中設置的算法參數組合,為了節省篇幅,其中N值只取 (K,β) 因子組合中算法性能最大的取值,其他4 列表示動態算法相較于兩個比對策略的總獎勵回報 (式(15)) 的提高率,取置信度為95%的置信區間.從表1 中可以看出,當λ1/45 時,無論哪一種參數組合,重規劃動態調度算法生成的方案都要優于比對策略,特別是當N28,K2 000,β0.5 時 (表1 中粗體字所示) 效果最好.另外,近似函數為神經網絡模型時,調度性能要明顯超過基于線性回歸模型的近似函數,這主要是因為調度算法中用基函數表示的影響因素相互交織,呈非線性關系,所以用神經網絡擬合效果較好.

3.3 性能指標比較測試

圖4 顯示了策略評估迭代次數K2 000 時,無論步長參數β取何值,相較于比對策略A,動態調度算法的性能都為最佳值.當K在增加到2 000前,動態算法的性能逐漸提高;當大于2 000 后,性能開始下降;在4 000 次迭代時性能明顯下降.主要原因是在K4 000 時,本仿真實驗的樣本數據集增加到一定閾值,導致神經網絡模型過擬合,從而產生低效率的調度結果.另外,從表1和圖4 都可以看出,β取較小值 (0.3 或0.5) 時,算法收斂速度較慢,能夠增加算法的調度效果.

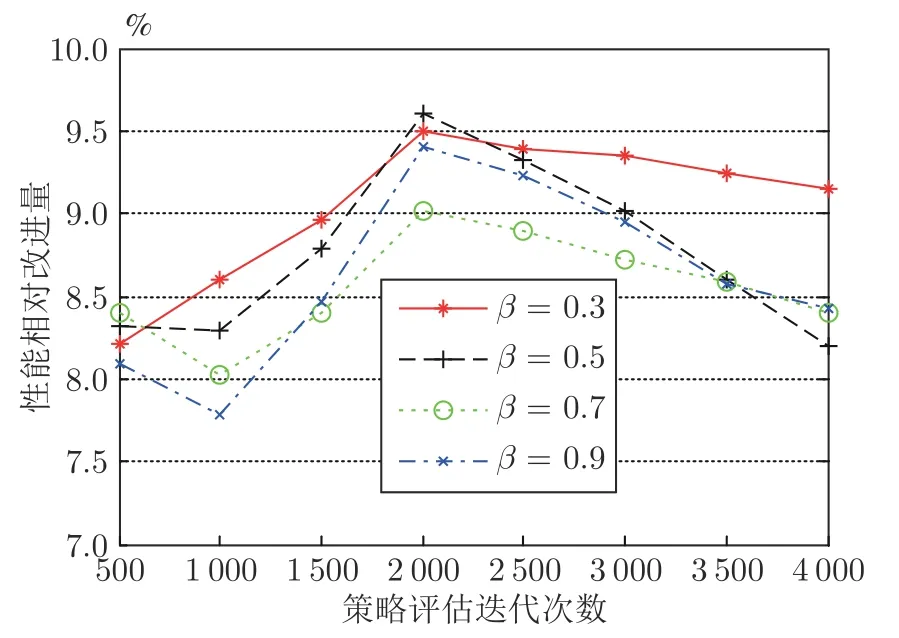
圖4 相較于比對策略A 的性能改進Fig.4 Improvement compared to policy A

表2 的第1 列為調度策略;第2 列和第3 列分別為當N28,K2 000,β0.5 時,不同優先級的保障申請響應時間 (從發出申請至保障分隊到達的時間間隔) 的置信區間 (置信度為95%);第4 列為調度方案V值提高百分比的置信區間.從表2 可以看出,具備搶占調度能力的策略B和動態調度算法都比不具備搶占能力的策略A 性能好,另外還有一個現象也需要引起注意,隨著第4 列顯示的性能提高,在緊急保障申請的響應時間減少的同時,一般保障申請的響應時間卻在增加.估計這與搶占調度特性有關,它搶占低優先級保障任務轉而去執行高優先級任務,導致低優先級任務服務時間延長.

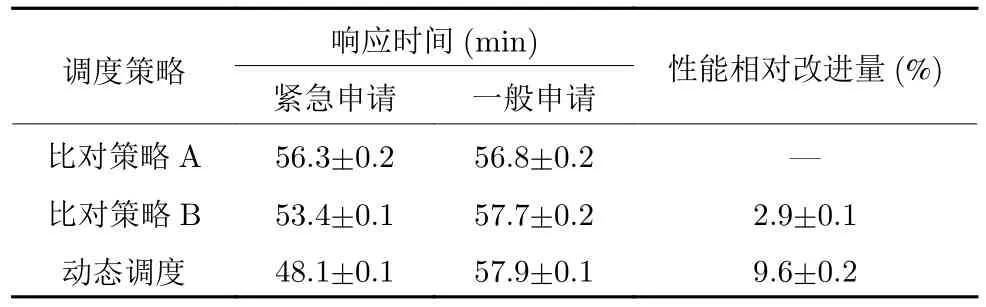
表2 動態算法和比對策略的性能比較Table 2 Comparison of the algorithms and policies

為了進一步檢驗算法的魯棒性,在模擬一天24 小時的保障仿真中,對保障申請發生率λ和交戰區域位置進行了數次改變.從圖5 中可以看出,響應時間也相應發生了較大波動,但是動態調度算法性能還是明顯好于比對策略.

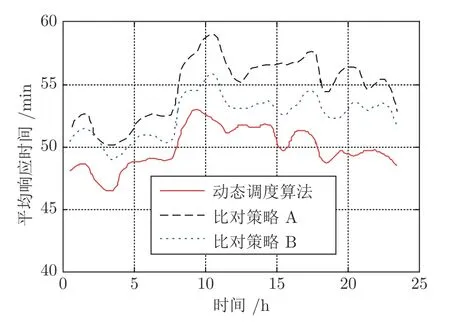
圖5 響應時間變化情況Fig.5 Response delay with time

保障申請率的變化對調度系統也有較大影響,為此,設置保障申請發生率λ從1/25 減小到1/65,圖6 反映了動態調度算法和比對策略B 相較于策略A 的性能相對改進量變化情況.λ減小意味著保障申請發生率減小,動態調度算法和策略B 的性能相對改進量也逐漸減小,表示搶占調度和重部署帶來的性能優勢也在減小,因此在低強度戰場上動態調度算法性能優勢不明顯,在保障申請率較高的高強度戰場上搶占調度和重部署能力才能取得較明顯的效果.

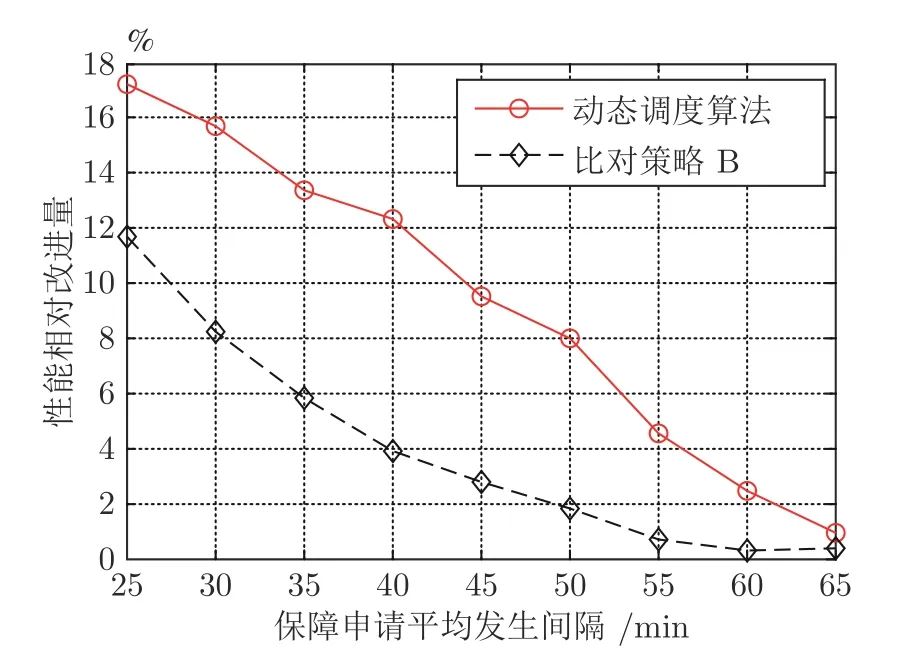
圖6 保障申請發生率的敏感性分析Fig.6 Sensitivity analysis of maintenance request occurrence rate

4 性能定性分析

最后通過4 個場景來定性分析重規劃能力的優勢.第1 個場景狀態中,假設某作戰部隊申請后裝保障,此時只有離它較遠的保障分隊空閑,離它較近的保障分隊預測能在較短時間內完成正在執行的任務.由于比對策略A和B 缺乏預測能力,會把較遠的空閑保障分隊分派出去,而動態調度算法需要最大化基于長期回報的獎勵函數,所以先把該次申請放入隊列,等候較近的保障分隊空閑后再分派.

在第2 個場景的系統狀態中,某保障分隊剛被分派執行某高烈度區域的一個低優先級保障任務,這時同樣區域發出了一個高優先級保障申請,此狀態下,除非指揮員發出新的分派指令,否則策略A將保持該保障分隊的任務不變.很明顯此時好的調度算法應該主動中斷保障分隊的當前任務,重新分派它執行高優先級的緊急任務,從而取得更高的回報價值.

考慮第3 個場景的系統狀態,某保障分隊剛被分派執行某高烈度區域的一個低優先級保障任務,這時另一個較遠距離的低烈度區域發出高優先級保障申請,此狀態下動態調度算法需要根據神經網絡模型的預測結果權衡,如果 “重規劃” 動作產生的狀態價值較小,則不應該實施搶占.

考慮第4 個場景的系統狀態,某保障分隊快要完成當前任務準備返回基地,這時一個離它較遠(超過剩余油料支持路程)的區域發出保障申請.該狀態下,比對策略的調度方案是要求該保障分隊返回原基地補充后再執行新任務.而具有重部署能力的動態調度算法會指示保障分隊前往距離申請點近的地方補充油料,從而更快地執行新任務.

綜上所述,與比對策略不同,動態調度算法的決策基礎是通過基函數組合的神經網絡模型,它能夠捕捉當前事件和可預測的未來事件帶來的影響,因此能夠產生更優的調度結果.

5 結束語

本文主要研究了戰時后裝保障中重規劃(搶占調度、重分配及重部署)問題,以便生成高質量的保障資源調度策略,提高后裝保障智能化水平.針對重規劃問題設計了一個無限時域馬爾科夫決策過程模型,其目標是最大化保障調度系統的長期折扣獎勵.為了解決重規劃模型的維度災問題,利用神經網絡對基函數進行非線性組合,從而達到逼近值函數的目的,并提出了基于強化學習策略迭代的神經網絡學習算法.最后設計了一個高強度分布作戰仿真場景,檢驗了不同問題特征及算法參數對調度性能的影響,驗證了動態調度算法的適用性.

本文中MDP 模型的描述是對保障調度適用的對象或場景的限制條件,對于超出該模型描述的保障調度,也具有一定的借鑒意義.另外,如果調度場景與對象變化較大,如作戰規模過大,保障基地數量位置動態變化時,由于機器學習能力限制,逼近函數(本文采用基函數+神經網絡)也需要相應調整.

下一步工作需要改進當前研究的一些不足之處,例如在高強度作戰中,可能某次保障申請需要的資源較大,超過了一個保障分隊或基地的能力,需要調度多個分隊協同保障.協同保障方面已經有一些相關研究成果,正在考慮如何與之結合.另一個重要研究方向是進一步擴展保障分隊的類型及相應特性,這樣可以比較不同保障分隊的調度性能.另外,錯誤定義的保障需求優先級會影響保障分隊的調度,這也是下一步需要解決的難點.