捷聯慣導與計程儀組合導航方法研究?

張晨陽 蔡 鵬 高大遠

（海軍潛艇學院 青島 266000）

1 引言

水下自主航行器（AUV）目前擁有廣泛的應用前景，在許多領域都可以看到它的身影，如何實現水下航行器的精確導航一直被諸多學者研究。水下單一的SINS 有自主性強，隱蔽性強等優點，缺點是系統誤差會隨著時間而增加，長航時情況下會引起導航精度下降。以SINS 為主體，引入其他導航技術，進行組合導航已經逐漸成為一個重要的研究方向。SINS/DVL組合導航系統使用DVL測量的速度參數對SINS 的參數誤差進行抑制，可以實現較高的導航精度，所以在水下導航時經常使用SINS/DVL組合導航方法［1］。

針對SINS/DVL 組合導航系統，一般使用擴展卡爾曼濾波（EKF）、無跡卡爾曼濾波（UKF）［2］等濾波方法。但是，EKF只選取非線性函數泰勒展開式的第一項，忽略了其他高階項，這樣會增加誤差，精度有限。而UKF 通過選取少量的采樣點來近似描述非線性函數，提高了濾波的精度，但是容易出現協方差矩陣負定的問題，而為了避免濾波算法發散，本文提出采用SRUKF［3］避免該問題，提高了濾波的可靠性。

當模型不夠精確或者系統噪聲時變時，會導致濾波效果較差，得到的導航參數精度較低。為了提高濾波算法的魯棒性，本文提出一種交互無跡卡爾曼濾波算法，提高了濾波算法的自適應性。最后，通過仿真實驗驗證提出算法的有效性。

2 SINS/DVL組合導航數學模型

2.1 狀態方程

SINS/DVL 組合導航誤差模型［4］分為SINS 誤差模型和DVL誤差模型。因為SINS垂直通道不穩定并且DVL 的垂直速度測量誤差較大，因為僅考慮水平通道問題。

DVL 的測速誤差［5］主要包括，速度偏移誤差δVd，刻度系數誤差δKc，偏流角誤差δΔ，因為偏流角誤差對測速影響較小，不予考慮。所以，DVL 的誤差方程如下：

式中：βd，βK分別表示速度偏移誤差和刻度系數誤差的相關時間；wd和wK分別是二者的零均值高斯白噪聲。

選擇SINS的狀態變量為經緯度誤差（δL,δλ），速度誤差（δvx,δvy），陀螺三個軸向的漂移（εx,εy,εz），平臺失準角（α,β,γ）。

所以建立狀態方程為

2.2 觀測方程

SINS/DVL組合導航采用速度組合［6］的方式，把SINS 得到的速度與DVL 測量的速度作差，并把此差值作為觀測量輸入到濾波器中。

SINS 得到的速度在導航坐標系下的投影為，即：

其中，Vn為速度真實值，為速度誤差值。

根據DVL的速度方程可得：

其中，DVL 在載體坐標系下的真實速度為，Vn為導航坐標系下速度的真實值，δKc為刻度系數誤差，δVDVL為隨機測量誤差，為姿態變換矩陣。

所以得到了系統的量測方程，即：

3 SRUKF濾波算法

由于在使用UKF 濾波算法的過程中，有可能出現協方差矩陣負定的情況，這樣會導致濾波算法不穩定，得到的狀態估計結果也變得發散。SRUKF在UKF［7］的框架下引入了協方差矩陣的平方根形式替代原來的協方差矩陣參與整個運算遞推過程，改善了濾波的準確度和可靠性。算法流程［8］此處不再贅述。

4 IMM-SRUKF算法

交互多模型算法（IMM）［9］針對不同的子系統設置不同的濾波器，每個子系統有特定的濾波器，不同濾波器運算時對應著不同子系統狀態空間方程。其中，每一個子系統代表的運行軌跡是不同的。

4.1 混合系統模型

假設混合系統一共有z個子系統，J1，J2,…,Jz分別代表子系統1 到子系統z，在初始時刻k=0時，子系統Jn發生概率：

μ1(0)，μ2(0),…,μz(0)滿足：

子系統之間的轉換概率：

m=1,2,…,z時，pm,n滿足：

混合系統由許多個非線性子系統構成，當處于子系統n時，系統一般表達式可描述為

x(k)?Rnx,u(k)?Rnu,y(k)?Rny,分別表示系統的狀態，輸入，輸出；An?Rnx×nx,Bn?Rnx×nx,Cn?Rnx×nx表示適宜維度矩陣；gn:Rnx→Rnx為非線性狀態函數；hn:Rnx→Rny為非線性觀測函數；w(k),v(k)表示過程噪聲和觀測噪聲，是相互獨立的高斯白噪聲向量，協方差矩陣分別為Q(k),R(k)。

4.2 IMM算法步驟

IMM的基本原理［10］是，在不同時刻每個濾波器對每個子系統進行狀態估計，把不同子系統狀態估計結果融合得到最終的狀態估計，并在某一時刻把前一時刻的最終狀態估計結果作為初始值，帶入系統狀態方程中，然后針對每個子系統進行濾波。算法最后更新某個子系統的發生概率，計算每個濾波器得到的狀態估計結果的權值，進行求和得到最終的系統處于這一時刻的狀態估計結果。

具體算法步驟［11～12］如下：

1）混合概率

μm(k-1)表示k-1時刻子系統m發生的概率，pm,n為轉移概率矩陣

2）輸入交互

(k-1|k-1) 為子系統m的狀態估計，Pm(k-1|k-1) 為子系統m的協方差矩陣，(k-1|k-1) 是子系統n的狀態估計，P0n,x(k-1|k-1) 是子系統n的協方差矩陣。

3）調用濾波算法

把(k-1|k-1)，P0n,x(k-1|k-1) 作為初始狀態，帶入到SRUKF濾波算法中。

4）子系統概率更新

似然函數：

子系統概率：

Sn(k|k-1)，(k|k-1)，yn(k)分別是子系統n在k時刻的觀測協方差矩陣，觀測估計值和觀測值。

5）對不同子系統輸出結果加權求和

(k|k)，(k|k)分別是子系統n在k時刻的最優狀態估計和協方差矩陣，(k|k)和P(k|k)分別是系統在k時刻最優狀態估計和協方差矩陣，(k|k)是k時刻系統的觀測估計值。

5 仿真實驗

將提出的IMM-SRUKF 算法應用到SINS/DVL組合導航系統中，進行仿真驗證。設定SINS 系統的

性能參數如下：陀螺儀的常值漂移和隨機漂移均設為0.05°/h，加速度計的常值漂移和隨機漂移均設為50μg，初始失準角：縱搖角：1.5°，橫搖角1.5°，航向角1.5° ；DVL 系統：速度偏移誤差δVd=0.10m/s，刻度系數誤差δKc=0.001，速度偏移誤差和刻度系數誤差的相關時間均為100s。

正常狀況下，SINS/DVL 的觀測噪聲沒有發生變化。采用SURKF 和IMM-SRUKF 算法得到速度誤差和位置誤差曲線如圖1 所示，從圖中可以看出采用SINS/DVL 組合導航提高了導航精度，抑制了速度誤差的增長，但是無法消除位置誤差的增長。當系統觀測噪聲沒有變化時，采用兩種算法得到誤差估計結果接近。

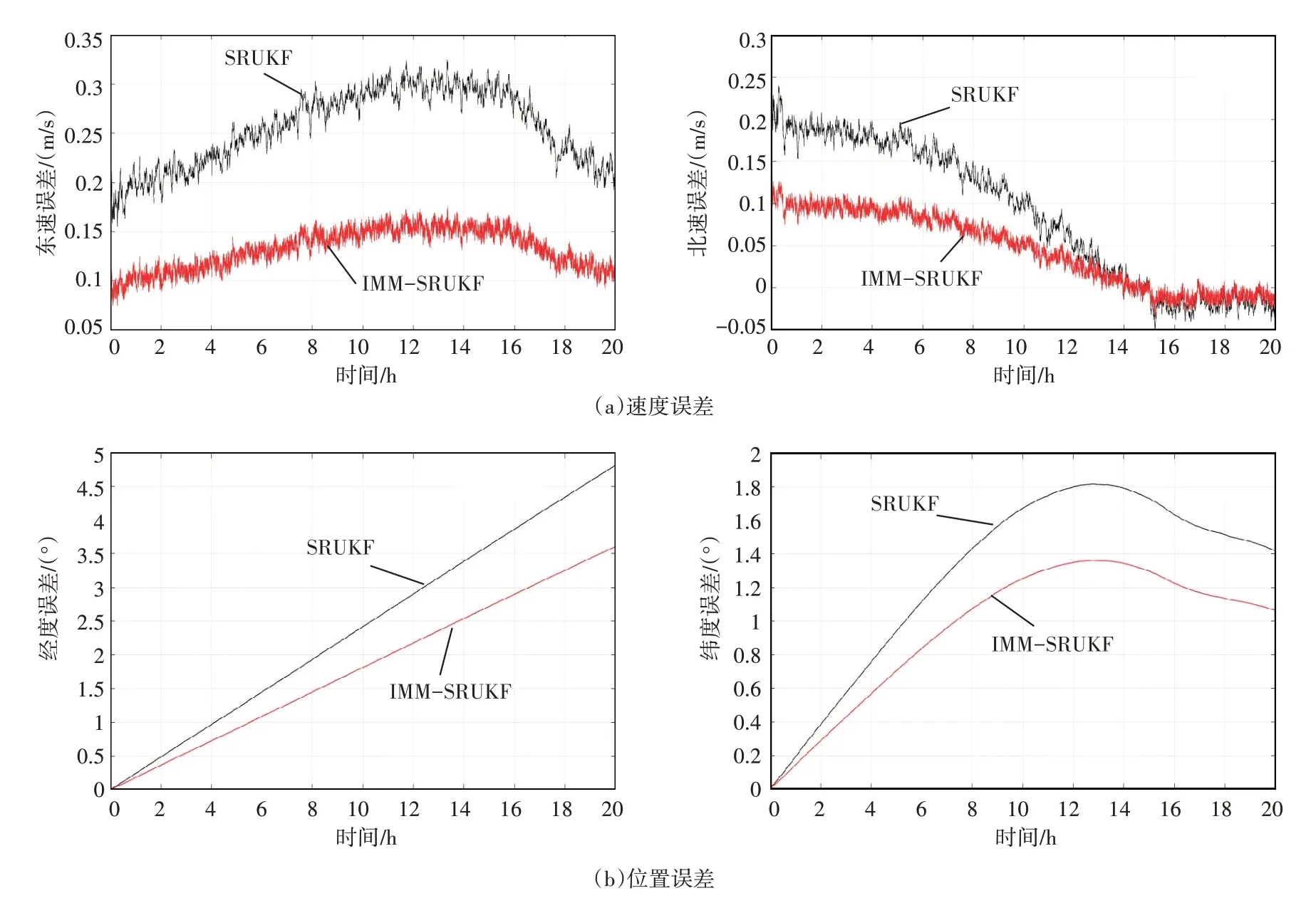
圖1 正常情況下的速度誤差和位置誤差

觀測噪聲服從高斯白噪聲分布，觀測噪聲協方差矩陣隨著時間推移會發生變化，在4h～5h和14h～15h 時將觀測噪聲增大為原來的4 倍，之后恢復正常。采用兩種濾波算法誤差估計結果如圖2 所示，當觀測噪聲發生突變時，采用兩種算法得到的速度誤差和位置誤差均發生了突變，導航的精度降低。但是單獨利用SRUKF 算法時不能有效地抑制噪聲變化帶來的誤差，并且累積了所產生的誤差。而采用本文所提出的IMM-SRUKF 濾波算法時，可以抑制噪聲帶來的誤差，并且產生的誤差并不會積累，可以保證導航的精度。

6 結語

本文研究了水下捷聯慣導系統（SINS）與多普勒計程儀（DVL）的組合導航問題，根據兩種系統的原理和誤差模型，建立了SINS/DVL 組合導航模型。在非線性系統濾波過程中，為了避免出現協方差矩陣負定的問題，提出利用SRUKF 算法，提高了濾波算法的穩定性。為了解決觀測噪聲變化帶來的濾波精度下降問題，提出了IMM-SRUKF 濾波算法，提高了算法的魯棒性。仿真結果證明，提出的濾波算法精度較高，有一定的自適應能力。