金氰化浸出過(guò)程混合建模及仿真算法分析研究
莫文水
(廣西現(xiàn)代職業(yè)技術(shù)學(xué)院,廣西 河池 547000)
目前,濕法冶金浸出過(guò)程反應(yīng)模型通常依據(jù)物料守恒、能量守恒及動(dòng)力學(xué)方程建立[1-5],但大部分研究依據(jù)理論仿真得出結(jié)論,與實(shí)際生產(chǎn)情況有偏差,試驗(yàn)參數(shù)無(wú)法固定,很難準(zhǔn)確獲取數(shù)據(jù),易導(dǎo)致研究結(jié)論與實(shí)際生產(chǎn)情況不相符[6-12]。
針對(duì)某金氰化浸出過(guò)程金浸出率無(wú)法精準(zhǔn)預(yù)測(cè)的問(wèn)題,首先建立了單級(jí)浸出動(dòng)態(tài)模型,再基于單級(jí)模型建立多級(jí)浸出動(dòng)態(tài)模型,并仿真驗(yàn)證多級(jí)浸出動(dòng)態(tài)模型浸出率的變化趨勢(shì);其次用基于免疫原理的RBF神經(jīng)網(wǎng)絡(luò)數(shù)據(jù)模型的學(xué)習(xí)算法模擬動(dòng)力學(xué)反應(yīng)速度方程,估算動(dòng)態(tài)機(jī)制模型中的未知參數(shù),與物料守恒方程串聯(lián),建立了浸出率預(yù)測(cè)的串聯(lián)混合模型,并根據(jù)模型的預(yù)測(cè)誤差進(jìn)行模型更新;最后通過(guò)在實(shí)際工業(yè)生產(chǎn)中的應(yīng)用,驗(yàn)證串聯(lián)混合模型的準(zhǔn)確性。
1 動(dòng)態(tài)模型的建立
1.1 單級(jí)和多級(jí)浸出動(dòng)態(tài)模型的建立
某金浸出工藝選擇氣力連續(xù)攪拌槽反應(yīng)器(CSTR)[13]為浸出槽,以NaCN溶液作浸出劑,采用多級(jí)串聯(lián)方式進(jìn)行氰化浸出。提前假設(shè)攪拌槽內(nèi)溫度分布均勻、礦漿攪拌均勻、反應(yīng)過(guò)程中不放熱、忽略反應(yīng)器中的物料隔離且浸出槽中礦漿pH恒定[8,13-14]。
根據(jù)金氰化浸出過(guò)程的物料守恒和動(dòng)力學(xué)反應(yīng),建立單級(jí)動(dòng)態(tài)模型[12]。物料守恒方程如下:
固相金守恒方程,
(1)
液相金守恒方程,
(2)
液相氰守恒方程,

(3)
式中:i—浸出槽級(jí)數(shù);ws,i—固相金品位,mg/kg;wl,i—液相金品位,mg/kg;ρ(CN-)i—液相氰根離子質(zhì)量濃度,mg/L;Qs,i—礦漿固相流量,kg/h;Ql,i—礦漿液相流量,kg/h;Q(CN-)i—浸出槽中添加的氰化鈉流量,mg/h;Ms,i—浸出槽中固相滯留質(zhì)量,kg;Ml,i—浸出槽中液相滯留質(zhì)量,kg;r(Au)i—金溶解速度,mg/(kg·h);r(CN-)i—氰離子的消耗速度,mg/(kg·h)。
將動(dòng)力學(xué)反應(yīng)方程[14]與實(shí)際樣本數(shù)據(jù)相結(jié)合,采用最小二乘法計(jì)算模型[15]參數(shù):

(4)
(5)
(6)

假設(shè)浸出過(guò)程穩(wěn)定,基于Qs,i和Ql,i質(zhì)量守恒可知:
Qs,i=Qs,i-1;
(7)
Ql,i=Ql,i-1。
(8)
假設(shè)浸出槽中所有反應(yīng)物充分混合,Qs,i和Ql,i之間的轉(zhuǎn)化關(guān)系式為:
(9)
式中:ρw,i—礦漿濃度,kg/L。忽略物料隔離,假設(shè)Qs,i和Ql,i與礦漿有相同的τi:
(10)
式中:ρs—礦漿中固相密度,g/cm3;ρl—礦漿中液相密度,g/cm3。
由式(9)、(10)分別得固相、液相滯留量為:
Ms,i=Qs,i×τi;
(11)
Ml,i=Ql,i×τi。
(12)
綜上,式(1)~(12)組成了單級(jí)浸出動(dòng)態(tài)模型。
使用ODE45計(jì)算該動(dòng)態(tài)模型得到ws,i,再由式(13)計(jì)算金浸出率:
(13)
基于單級(jí)浸出動(dòng)態(tài)模型,將串聯(lián)的每一級(jí)浸出槽的輸出變量作為下一級(jí)浸出槽的輸入變量,建立多級(jí)浸出動(dòng)態(tài)機(jī)制模型,從而得到每一級(jí)浸出槽中礦漿的固相金品位,之后由式(14)計(jì)算整個(gè)浸出過(guò)程金總浸出率:
(14)
式中:ws,0—礦漿初始固相金品位,mg/kg;ws,N—N級(jí)浸出后礦漿的固相金品位,mg/kg。
1.2 多級(jí)浸出動(dòng)態(tài)模型的仿真分析
采用六級(jí)浸出槽的浸出率試驗(yàn)數(shù)據(jù)對(duì)多級(jí)浸出動(dòng)態(tài)模型進(jìn)行模擬,并仿真分析不同輸入變量對(duì)浸出率變化趨勢(shì)的影響[14-16]。模型中相關(guān)變量取值見(jiàn)表1。
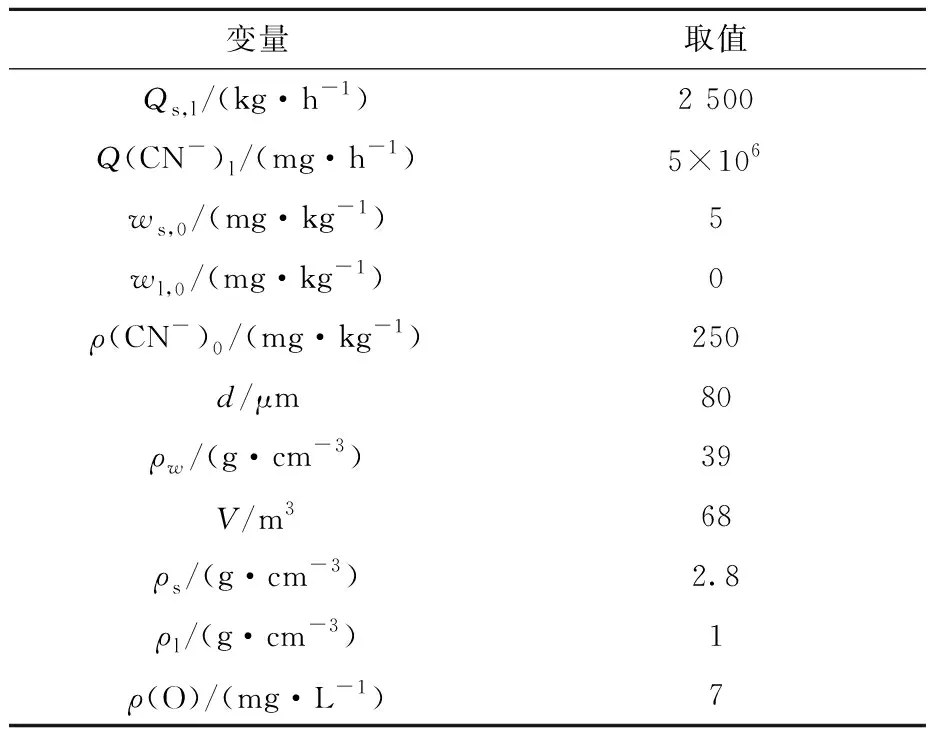
表1 多級(jí)浸出動(dòng)態(tài)模型中相關(guān)變量取值
分別以礦石流量、礦漿質(zhì)量濃度、氰化鈉添加流量、溶解氧質(zhì)量濃度及礦石平均粒徑為輸入變量,其余變量按照表1取值,仿真分析5個(gè)變量對(duì)金浸出率的影響,試驗(yàn)結(jié)果如圖1~5所示。
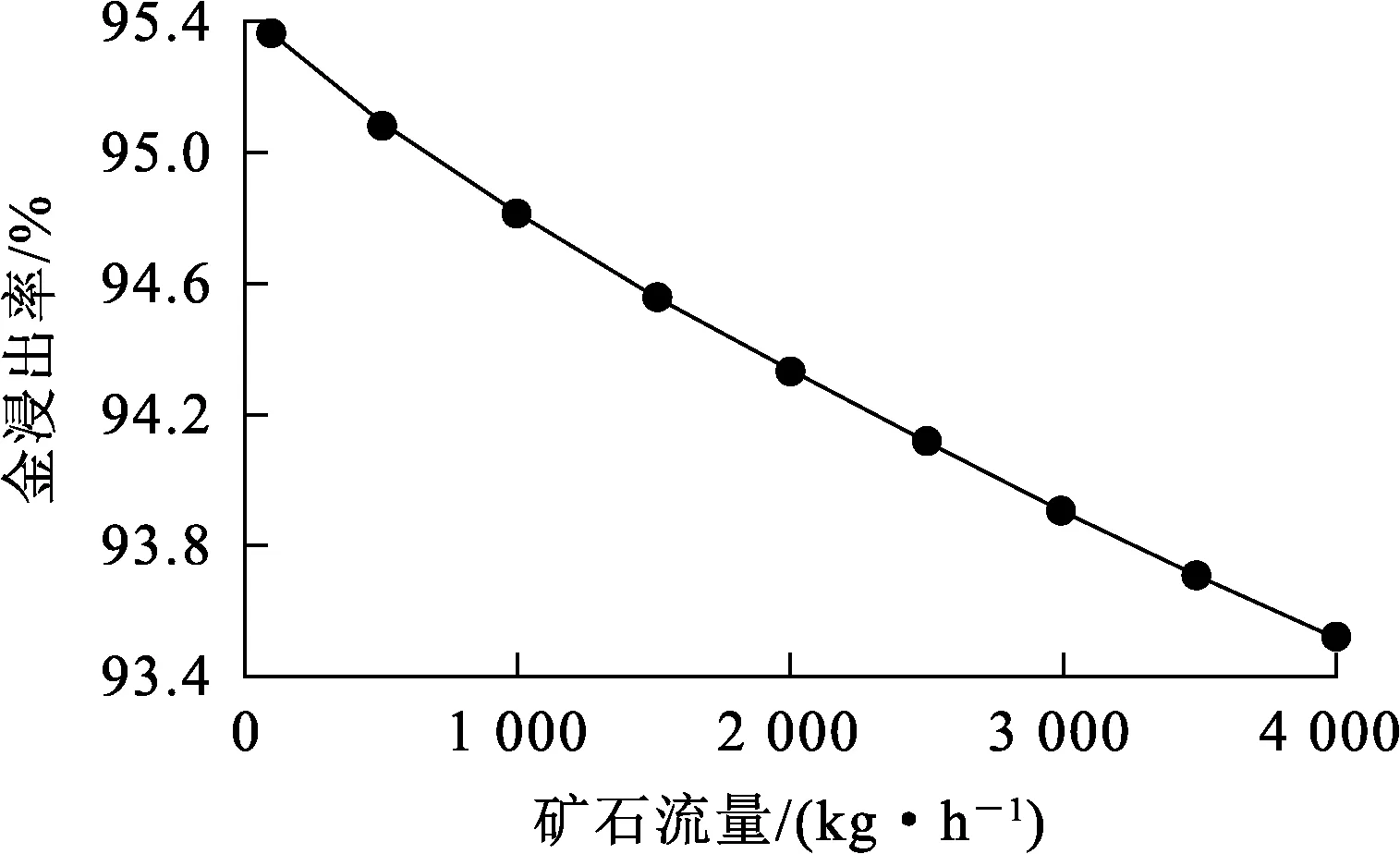
圖1 礦石流量對(duì)金浸出率的影響
由圖1看出:金浸出率隨礦石流量增大而降低。因?yàn)榈V石流量增大易導(dǎo)致礦漿在浸出槽中滯留時(shí)間變短,使礦漿無(wú)法與浸出劑充分反應(yīng),造成金浸出率降低。由圖2看出:金浸出率隨礦漿質(zhì)量濃度增大而提高,礦漿質(zhì)量濃度增至20 kg/L后,金浸出率趨于穩(wěn)定。這是由于礦漿質(zhì)量濃度過(guò)大,黏度增大,導(dǎo)致金浸出不完全。由圖3看出:金浸出率隨氰化鈉添加流量增加先快速升高;氰化鈉添加流量增至50 mg/h后,金浸出率升高幅度趨緩慢。由圖4看出:金浸出率隨溶解氧質(zhì)量濃度增加而提高,溶解氧質(zhì)量濃度增至5 mg/L以后,金浸出率的增長(zhǎng)幅度趨緩。由圖5看出:浸出率隨礦石平均粒徑增大而降低。礦石平均粒徑增大會(huì)導(dǎo)致化學(xué)反應(yīng)不充分,使得浸出率減小。通過(guò)以上對(duì)動(dòng)態(tài)機(jī)制模型中各輸入變量對(duì)浸出率影響的仿真分析,幫助我們更好的分析了浸出率的影響因素情況及動(dòng)態(tài)特性,為實(shí)際生產(chǎn)過(guò)程提供正確的理論指導(dǎo)。

圖2 礦漿質(zhì)量濃度對(duì)金浸出率的影響

圖3 氰化鈉添加流量對(duì)金浸出率的影響

圖4 溶解氧質(zhì)量濃度對(duì)金浸出率的影響

圖5 礦石平均粒徑對(duì)金浸出率的影響
2 基于RBF神經(jīng)網(wǎng)絡(luò)的串聯(lián)混合模型
實(shí)際浸出過(guò)程中,動(dòng)力學(xué)反應(yīng)速度無(wú)法直接測(cè)量,因此,以浸出過(guò)程動(dòng)態(tài)模型為基礎(chǔ),采用徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)(RBFNN)數(shù)據(jù)建模法[17-21]建立浸出過(guò)程的動(dòng)力學(xué)反應(yīng)速度模型,估算浸出過(guò)程動(dòng)態(tài)模型中的未知參數(shù),再與物料守恒方程串聯(lián),從而建立預(yù)測(cè)浸出率的串聯(lián)混合模型。
2.1 徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)
RBF神經(jīng)網(wǎng)絡(luò)是一種具有單隱層的三層前饋網(wǎng)絡(luò),包括輸入層、隱含層和輸出層。本研究主要討論神經(jīng)網(wǎng)絡(luò)的訓(xùn)練算法,包括基礎(chǔ)設(shè)置與公式。
設(shè)輸入層、隱含層、輸出層的節(jié)點(diǎn)數(shù)分別為n、m、s,有N組輸入輸出樣本對(duì)應(yīng)(X(i),Y(i),(i=1,2,…,N)),其中X(i)是n維向量,Y(i)是s維向量,輸入層連接隱含層的權(quán)值設(shè)為1,n維徑向基函數(shù)則作為隱含層節(jié)點(diǎn)的激活函數(shù):
(15)

徑向基函數(shù)通常選取Gaussion函數(shù):

(16)
式中,σj—第j個(gè)以cj為中心的高斯函數(shù)寬的向量。
一般輸出可表示為:
(17)

式(17)的矩陣形式為:
Y=ΦW,Φ∈RP×(m+1),W∈R(m+1)×s。
(18)


RBF神經(jīng)網(wǎng)絡(luò)算法是目前常用的混合學(xué)習(xí)算法之一,主要包含兩個(gè)階段。
第一階段是非監(jiān)督學(xué)習(xí)階段,需要得出徑向基函數(shù)中的數(shù)據(jù)中心和寬度,通常采用K-means聚類(lèi)算法。首先定義參數(shù):P個(gè)樣本{X1,X2,…,XP},M個(gè)隱節(jié)點(diǎn)數(shù),c(k)是第k次迭代的中心。其次隨機(jī)確定M個(gè)互不相同的向量c1(0),c2(0),…,cM(0)作為初始聚類(lèi)中心;隨后計(jì)算輸入樣本點(diǎn)與選擇的聚類(lèi)中心點(diǎn)的歐式距離并比較得出距離最小值的節(jié)點(diǎn):

(19)
令r表示該隱含層節(jié)點(diǎn)下標(biāo),根據(jù)式(20)與聚類(lèi)中心的最小歐幾里得距離對(duì)每一個(gè)輸入樣本Xp進(jìn)行歸類(lèi):
(20)
式中:r(Xp)—Xp被分為r類(lèi)。
同理將所有樣本分為M個(gè)子集U1(k),U2(k),…,UM(k),代表M個(gè)聚類(lèi)域。采用競(jìng)爭(zhēng)學(xué)習(xí)的規(guī)則對(duì)各個(gè)聚類(lèi)中心進(jìn)行調(diào)整:
(21)
式中:η—學(xué)習(xí)率,取值范圍為[0,1]。
其次,令k=k+1,判斷c的改變量是否小于預(yù)設(shè)閾值,是則利用聚類(lèi)中心之間的距離確定徑向基函數(shù)的擴(kuò)展常數(shù);否則通過(guò)式(19)重新計(jì)算歐氏距離并尋找距離最小值的隱含層節(jié)點(diǎn),并按照以上步驟繼續(xù)計(jì)算直至c的改變量小于預(yù)設(shè)閾值。

混合學(xué)習(xí)算法雖有一定優(yōu)點(diǎn),但也存在RBF神經(jīng)網(wǎng)絡(luò)的隱含層數(shù)需要提前根據(jù)試驗(yàn)確定,其數(shù)值的不同會(huì)很大程度影響聚類(lèi)的性能等缺點(diǎn)。
2.2 基于免疫原理的RBF神經(jīng)網(wǎng)絡(luò)模型學(xué)習(xí)算法
針對(duì)混合學(xué)習(xí)算法存在的不足,研究人員提出了免疫網(wǎng)絡(luò)模型[12],改進(jìn)后可用于選擇RBF神經(jīng)網(wǎng)絡(luò)隱含層數(shù)據(jù)中心(隱含層數(shù)),無(wú)需提前試驗(yàn)確定。
假設(shè)一組向量作為輸入數(shù)據(jù)X={x1,x2,…,xN},其中向量xi=[xi1,xi2,…,xip]T∈Rp(i=1,2,…,N)。確定RBF神經(jīng)網(wǎng)絡(luò)的數(shù)據(jù)中心需得到一個(gè)新的數(shù)據(jù)集作為聚類(lèi)的輸入數(shù)據(jù),設(shè)該數(shù)據(jù)集為C={c1,c2,…,ch},cj=[c1j,c2j,…,cpj]T∈Rp,j=1,2,…,h,其中h遠(yuǎn)小于N。
首先定義抗原與抗體間的相互作用強(qiáng)度為親和力,設(shè)輸入數(shù)據(jù)xi和數(shù)據(jù)中心cj之間的親和力為aij;定義抗體與抗體間的相互作用強(qiáng)度為相似度,設(shè)數(shù)據(jù)中心ci與數(shù)據(jù)中心cj之間的相似度為sij;其中aij與sij的表達(dá)式分別為:

(22)
(23)

改進(jìn)后的免疫網(wǎng)絡(luò)模型算法[12]如下:

(24)
式中:ak—抗體ck的親和力,ak越高,突變率越低。
2)數(shù)據(jù)中心集突變后,重新計(jì)算xi與L’中Nc個(gè)數(shù)據(jù)中心的親和力,并選取ξ%個(gè)親和力最大的數(shù)據(jù)中心,生成數(shù)據(jù)中心記憶集m。設(shè)定閾值σd,消除m中親和力比σd小的數(shù)據(jù)中心,生成新的數(shù)據(jù)中心記憶集m’。為了清除突變集中相互識(shí)別的數(shù)據(jù)中心防止產(chǎn)生抑制,設(shè)定閾值σs,計(jì)算m’中各數(shù)據(jù)中心間的相似度sij,并比較sij與σs;若sij>σs,保留該數(shù)據(jù)中心,反之則清除。
3)將全部數(shù)據(jù)中心記憶集m’合并生成總數(shù)據(jù)集M。計(jì)算M中所有數(shù)據(jù)中心間的相似度sij,同理利用sij>σs清除不同數(shù)據(jù)集中相似的數(shù)據(jù)中心,完成免疫系統(tǒng)中的網(wǎng)絡(luò)抑制過(guò)程,生成最終數(shù)據(jù)集M’。
4)最后,隨機(jī)選取一定數(shù)量的新數(shù)據(jù)中心替換C中對(duì)應(yīng)數(shù)量親和力低的數(shù)據(jù)中心,重復(fù)以上步驟。達(dá)到預(yù)設(shè)的最大遞推次數(shù)后的M’即為所求的RBF數(shù)據(jù)中心集。
綜上,即可確定RBF神經(jīng)網(wǎng)絡(luò)的隱含層數(shù)。隨后,采用遞推最小二乘法求解線性方程組Y=ΦW中的W,即可估計(jì)輸出層權(quán)值。計(jì)算P(k):
(25)
式中:P(k)—逆相關(guān)矩陣;Z(k)—隱含層節(jié)點(diǎn)的輸出值;λ—遺忘因子,一般取0<λ<1。
更新網(wǎng)絡(luò)權(quán)值:
W(k)=W(k-1)+g(k)[y(k)-ZT(k)W(k-1)]。
(26)
式中:W(k)—權(quán)值矢量;y(k)—神經(jīng)網(wǎng)絡(luò)的期望輸出。
給出終止條件:
(27)
式中:J(k)—誤差;ε—誤差滿足的迭代停止值。若|J(k)-J(k-1)|<ε,則此時(shí)的W為最終值;反之,轉(zhuǎn)到計(jì)算P(k)值繼續(xù)迭代。由此,確定了輸出層的權(quán)值。
2.3 仿真分析
基于某金精煉廠浸出工藝采樣數(shù)據(jù),對(duì)串聯(lián)混合模型進(jìn)行仿真驗(yàn)證。為了方便對(duì)比分析,建立一個(gè)基于免疫原理RBF神經(jīng)網(wǎng)絡(luò)的純數(shù)據(jù)模型(RBFNN數(shù)據(jù)模型)。將輸入與輸出數(shù)據(jù)之間擬合成非線性函數(shù)關(guān)系,模型的方程式如下:

(28)
對(duì)串聯(lián)混合模型仿真驗(yàn)證的變量取值參見(jiàn)表1,免疫學(xué)習(xí)算法中RBFNN數(shù)據(jù)模型參數(shù)取值見(jiàn)表2。

表2 免疫學(xué)習(xí)算法中RBFNN數(shù)據(jù)模型參數(shù)取值
兩種模型預(yù)測(cè)效果的評(píng)價(jià)指標(biāo)如下:
1)最大絕對(duì)誤差(MAE)
(29)
2)均方根誤差(RMSE)
(30)
選擇200組數(shù)據(jù)作為樣本集,仿真分析浸出過(guò)程金浸出率的動(dòng)態(tài)變化過(guò)程;再選取25組浸出達(dá)到穩(wěn)態(tài)后的數(shù)據(jù)作為樣本進(jìn)行驗(yàn)證,結(jié)果如圖6、7所示。

圖6 金浸出率動(dòng)態(tài)變化的預(yù)測(cè)結(jié)果

圖7 穩(wěn)態(tài)金浸出率的預(yù)測(cè)結(jié)果
串聯(lián)混合模型和RBFNN數(shù)據(jù)模型的誤差對(duì)比結(jié)果見(jiàn)表3。可以看出:基于串聯(lián)混合模型的MAE和RMSE都小于RBFNN數(shù)據(jù)模型的對(duì)應(yīng)數(shù)據(jù)。說(shuō)明串聯(lián)混合模型預(yù)測(cè)值精度和泛化能力更高,在實(shí)際工業(yè)中應(yīng)用效果會(huì)更好。

表3 串聯(lián)混合模型和RBFNN數(shù)據(jù)模型的誤差對(duì)比結(jié)果
3 串聯(lián)混合模型的更新及仿真分析
由于浸出過(guò)程具有時(shí)變性,模型精度會(huì)隨時(shí)間延長(zhǎng)而下降,若要精準(zhǔn)預(yù)測(cè),所建立模型需要具有更新能力。因此,需要通過(guò)對(duì)比預(yù)測(cè)值yp(t)和實(shí)際值y(t)之間誤差判斷是否需要進(jìn)行模型更新。具體操作步驟為:1)初始化相關(guān)參數(shù)并設(shè)定標(biāo)準(zhǔn)誤差值E=0.01;2)結(jié)合初始數(shù)據(jù)通過(guò)串聯(lián)混合模型得到金浸出率預(yù)測(cè)值,將輸入輸出數(shù)據(jù)添加到歷史數(shù)據(jù)中;3)再次計(jì)算得到金浸出率預(yù)測(cè)值;4)計(jì)算誤差e(t)=|y(t)-yp(t)|,若e(t) 選取200組數(shù)據(jù)作為樣本集,仿真分析浸出過(guò)程金浸出率的動(dòng)態(tài)變化過(guò)程;選取25組數(shù)據(jù)進(jìn)行測(cè)試,驗(yàn)證混合模型更新策略的有效性。預(yù)測(cè)結(jié)果如圖8、9所示。串聯(lián)混合模型和改進(jìn)混合模型誤差對(duì)比結(jié)果見(jiàn)表4。由圖8、9和表4看出:模型更新后的預(yù)測(cè)值更接近實(shí)際值,說(shuō)明對(duì)串聯(lián)混合模型進(jìn)行更新,可提高模型的準(zhǔn)確性。 圖8 金浸出率動(dòng)態(tài)變化的預(yù)測(cè)結(jié)果 圖9 穩(wěn)態(tài)金浸出率的預(yù)測(cè)結(jié)果 表4 串聯(lián)混合模型和更新串聯(lián)混合模型的誤差對(duì)比 針對(duì)金氰化浸出過(guò)程建立了一種具有高預(yù)測(cè)精度的串聯(lián)型混合模型,并通過(guò)計(jì)算實(shí)際值與預(yù)測(cè)值之間的誤差對(duì)模型進(jìn)行更新,提高了模型的準(zhǔn)確性。但由于實(shí)際生產(chǎn)過(guò)程具有一定的復(fù)雜性,所建立串聯(lián)混合模型在實(shí)際應(yīng)用過(guò)程中仍有一定的局限性,還有待進(jìn)一步研究改進(jìn)。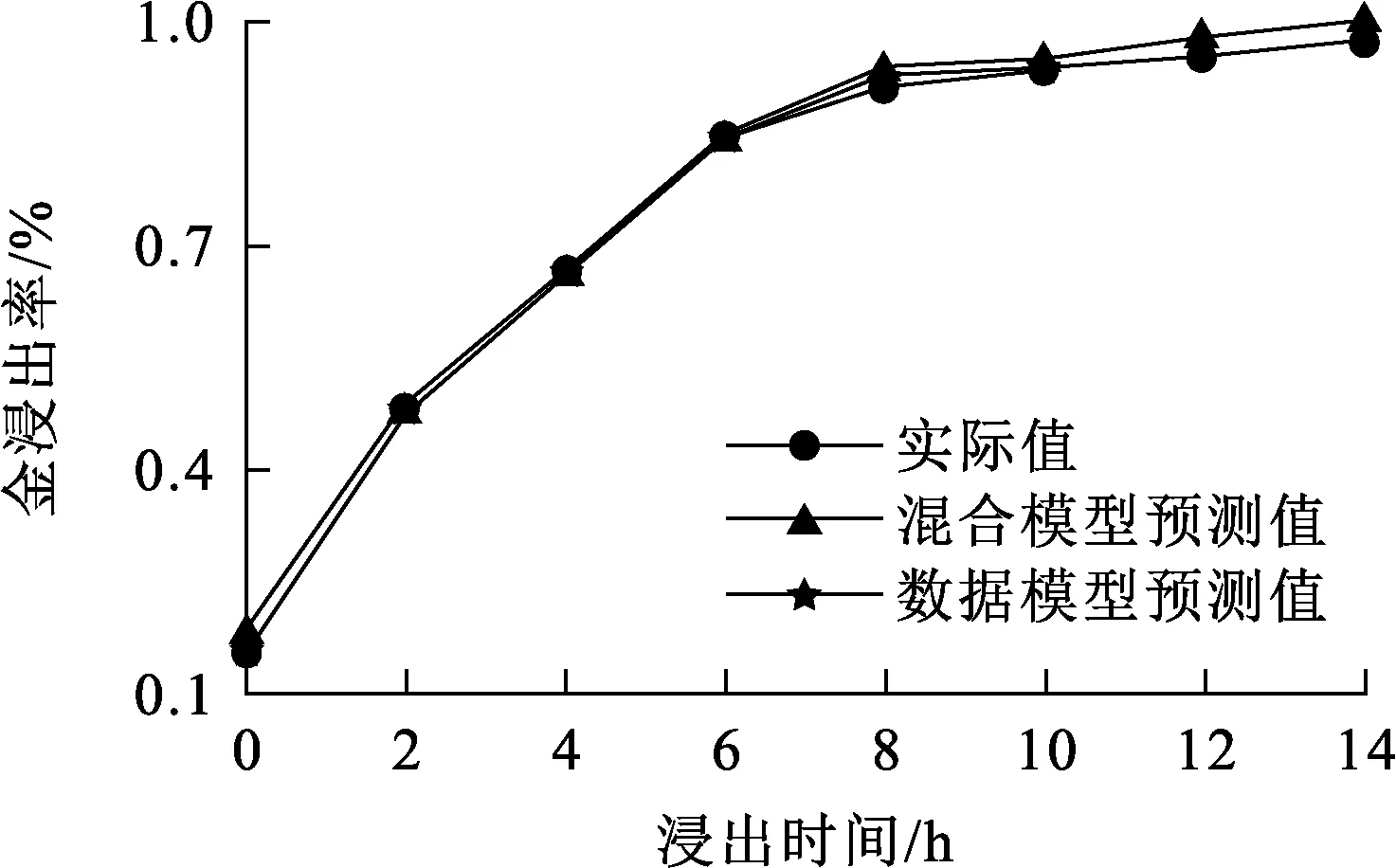


4 結(jié)論

