計算極限的20 種方法在大學生數學競賽中的應用
賴怡冰
(廣東理工學院 基礎課教學研究部,廣東 肇慶 526000)
微積分建立在極限理論的基礎上,極限反映了變量的局部性態與變化趨勢,是實現無窮運算的唯一方法。極限理論主要包括其存在性、相關性質與極限的計算等方面的內容,工科數學尤以極限的計算為主。
極限思想在現代數學乃至物理學等學科中,有著廣泛的應用,這是由它本身固有的思維功能所決定的。微積分研究的對象是函數,研究的工具叫極限,極限的最實際的作用就是可以進行微積分,進而進行更高層次的研究。極限可以把很多看似不可能的東西合理化,比如無窮、無限逼近等都可以在極限的框架下合理地運算和理解,其本質就是提出了一種很特殊的運算法則。由此可見,極限在高等數學教學、考研數學和大學生數學競賽中的重要性[1-2]。
學好極限的思想,并學會靈活的應用,顯得尤為重要。目前,全國大學生數學競賽已經成功舉辦了14 屆。大學生數學競賽的目的是激勵大學生學習數學的興趣,培養學生分析問題、解決問題的能力,提升我國高等學校人才培養質量,促進高等學校數學課程建設,并為青年學子搭建一個展示數學思維能力和學習成果的平臺,助力數學及復合型創新本科人才的成長[3-4]。 計算極限有哪些方法,這些方法如何體現在大學生數學競賽中,學生如何去歸納總結,發散思維,創新應用值得深入研究。,如果
1 理論
為了更好地理解、掌握與應用極限的計算方法與技巧,本文通過歷屆全國大學生數學競賽真題將計算極限常用的20 種方法進行歸納總結,并進行介紹[1-6]。方法1:冪指函數的對數函數法
[g( x )]f(x)冪指函數,即底為函數,冪也為函數的函數。
基于 f(x)= ex(x ∈R)在全體實數范圍內的連續性,函數的極限等于極限的函數,即要 求g( x )>0。
方法2:冪指函數的第二個重要極限法
如果x*在的某個去心鄰域內 f(x)>0,則有,則∞1 極限式為類型,基于重要極限的方法來計算函數的極限,即
冪指函數的極限式結構:∞1 未定型的極限的計算思路與步驟可以概括如下幾步:
第一步:判定類型是否為∞1 ;
第二步:改寫結構為∞+ 0)1( ;
第三步:轉換極限為∞0?e ;
第四步:轉換;∞0 ;
第六步:寫出最終結果為ae 。
第五步:計算極限 ?→a
對于不符合這種未定型結構的冪指函數的極限式的極限計算,一般采用對數函數法。
方法3:冪指函數中用等價無窮小求極限
(1)∞1 型,先將冪指函數取對數,再用等價無窮小求極限。
(2)0∞或00中無窮小量可以直接做等價無窮小替換。
設f(x)0,g(x)0 且,f(x)~g(x),f1(x)~g1(x)則
推導:
方法4:利用洛必達法則求極限
定理1(1)函數f(x),g(x)都趨于0(無窮大);(2)在x*某去心鄰域內,f '(x),g'(x)都存在,且g'(x)≠0;
注:(1)先有導函數構成的極限式極限存在,才有原來極限的極限存在并且極限值相等;(2)適用于分式類型的極限式;(3)適用于或未定型極限。
洛必達法則計算極限的步驟:
第三步:分子、分母函數的可導性及分母函數及導數是否為零;
方法5:利用等價無窮小代換求極限
定理2 設fj(x)( j=1, 2)和gj(x)( j=1, 2)均為過程的無窮小xx*,fj(x), gj(x)( j=1, 2)在相應的去心鄰域中不等于0,且有f1(x)~f2(x)(xx*),g1(x)~g2(x)(x x*)
注:一般適用于相乘的因式函數用等價無窮小替換簡化極限計算,即等價無窮小的替換只能在商或積的情況下進行。
使用等價無窮小簡化極限計算的基本原則:
(1)乘因式替換原則。例如:
(2)和差代替原則。
②不等價的無窮小相加減可以考慮使用等價無窮小化簡計算,例如:。
方法6:四則運算法則
設lim f(x)及limg(x)都存在(假定x 在同一變化過程中),則有下列運算法則:
lim [f(x)±g(x)]=lim f(x)±limg(x);
lim [f(x)·g(x)]=lim f(x)·limg(x);(lim g(x) 0)≠ 。
注:極限的四則運算法則只有在極限存在,以及有限個的條件下才可以用。
方法7:利用無窮小與函數極限之間的關系求極限
lim f(x)=A 的充要條件是f(x)=A +a(x),其中(x)是xx0時的無窮小量。
方法8:泰勒公式法
當函數f(x)在x=0 處具有n 階導數,那么存在x=0 的一個鄰域,對于該鄰域內的任意x,有
(帶皮亞諾型余項的麥克勞林公式)
注:(1)一般適用于自變量的變化過程為趨于0 的變化過程
(2)階數一般與題目中出現的冪函數最高次數相同。
方法9:導數的定義法
導數的定義式:
方法10:利用極限存在的2 個原理計算極限
(1)夾逼準則:設3 個數列{xn},{yn},{zn}滿 足xn≤yn≤zn,且,則。
(2)單調有界原理:單調增(減)有上(下)界的數列必定收斂。
方法11:利用拉格朗日中值定理求極限
若函數f (x)在[a, b]上連續,在(a, b)內可導,則),∈( ab?ξ ,使得f (a)-f (b)=f '(ξ)(b-a).
方法12:定積分定義法
方法13:積分中值定理
(2)廣義積分中值定理:如果函數f(x), g(x)都在[a, b]閉區間上連續,并且g(x)在[a, b]上不變號,則在閉區間[a, b]上必有一點ξ,使得
方法14:利用施篤茲(Stolz)定理計算極限
設數列{yn} 單調增加且,如果存在或為∞,則
方法15:基于數列極限定義與定積分等式的極限證明方法
抽象數列、函數極限的驗證一般考慮極限定義法。證明遞推數列極限存在并計算極限值的定義法:
假設極限存在→利用遞推式計算極限值→驗證極限
解題過程中結合定積分基本計算公式的逆運算、函數的單調性、定積分的保序性等。
注:(1)用特殊法探索可能的極限值是整個驗證過程的關鍵;(2)積分等式給出了改寫數學描述的方向;(3)數列極限的定義是整個驗證過程的理論依據;(4)轉換問題描述是貫穿始終的探索解題思路的基本思想與方法。
方法16:基于常值級數收斂定義的部分和數列極限計算方法
前n 項的部分和式極限的計算問題:不含有n,只含有k,級數的部分和數列,xn是常值級數的部分和數列,f (n)是常值級數的求和。
方法17:用級數的斂散性計算極限
級數的斂散性就是其部分和數列的極限問題,所以數列極限與級數的斂散性很難分割。對某些形式(特別是無窮和形式)的極限借助于級數的相關知識來解決會更為方便。
方法18:基于極限定義與子數列的斂散性驗證極限結論的方法
方法19:特殊法求極限
特殊法的使用有前提條件,要求:(1)所求的極限要存在;(2)極限在參數的取值范圍內,極限值都相等,不需要另外討論參數的取值范圍可能會有不同極限值的結果。
方法20:初等變形法
用初等運算、變量代換、恒等變形、三角函數極限式、平方差公式、二倍角公式、遞推法等方法將極限式化簡。
為了更好地說明計算極限的20 種方法在大學生數學競賽中的應用情況,下面列出歷屆大學生數學競賽中考到極限的屆數、題號、分值、用到的方法以及計算極限的20 種方法在歷屆大學生數學競賽中運用的次數情況、分值變化趨勢,具體情況(表1 和圖1)。
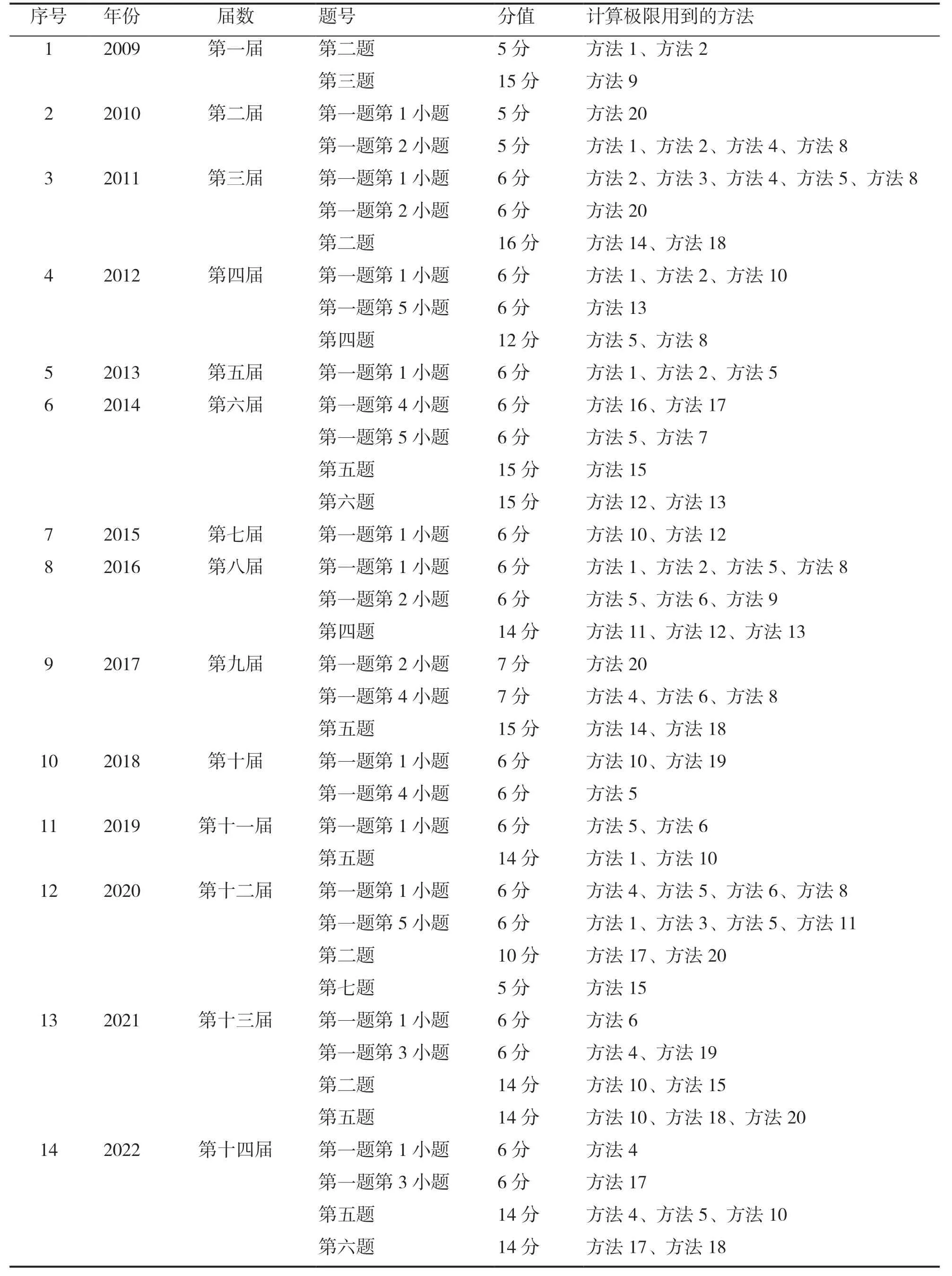
表1 計算極限的20 種方法在大學生數學競賽中的應用情況
從表1 和圖1 可以看出,在歷屆大學生數學競賽中,計算極限的20 種方法里運用得最多的是方法5 利用等價無窮小代換求極限,有11 次,方法1 冪指函數的對數函數法、方法4 洛必達法則和方法10 利用極限存在的2 個原理計算極限,都是7 次。圖2 顯示,從第一屆到第十四屆共14年的數學競賽都考到了極限的知識,所占分值比例從原來的下降、上升、下降、上升的變化規律轉變為逐漸上升的趨勢,特別是從第十屆開始到第十四屆,從原來的12 分增加到40 分,對于總分100 分的競賽題來說,所占分值較大,可見極限計算在競賽中的重要地位。
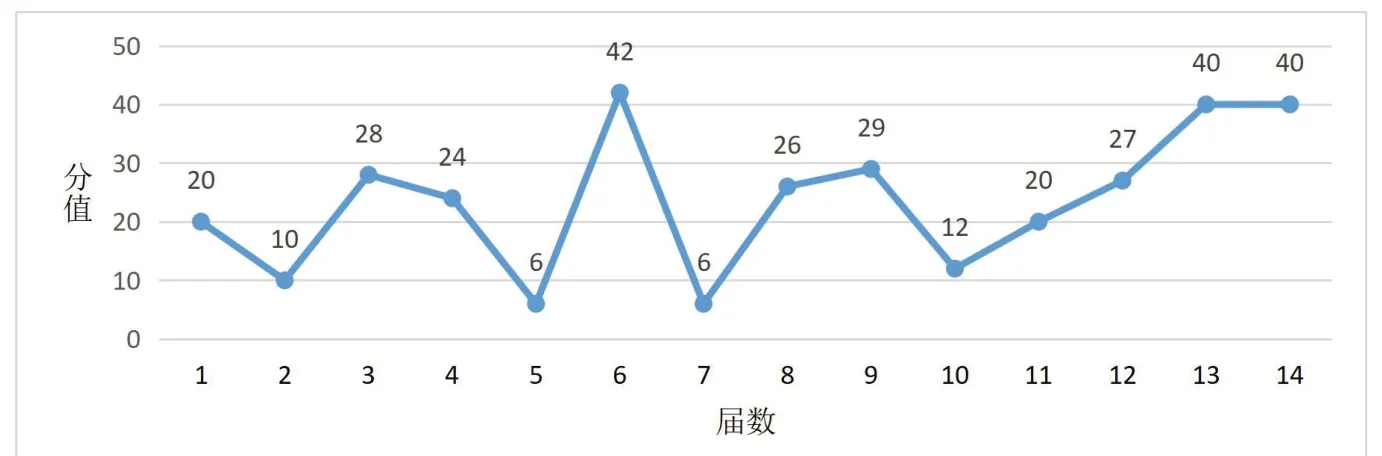
圖2 歷屆大學生數學競賽極限占的分值情況
2 實例
為了更好地說明計算極限的20 種方法在歷屆競賽中的應用,下面給出幾道典型的歷年大學生數學競賽真題,從解題過程中可以清晰明了地看出各種方法的應用,有助于理解極限的知識,限于篇幅,只給出一部分真題解答過程。
解:冪指函數的對數函數法,洛必達法則
解:包含了抽象函數的,由已知極限求未知極限的問題。通常的做法:根據已知極限,借助無窮小與函數極限之間的關系,寫出未知抽象函數相對具體的表達式,然后將抽象函數表達式代入要求極限的極限式,推導計算得到未知極限。
解:
例4(2016 年,6 分)若f (x) =0,f '(1) 存在,求極限。
解:利用導數的定義求極限
例5 (2017 年,7 分) 設f (x) 有 二 階導 數 連 續, 且f (0) = f '(0) = 0,f ''(0) = 6, 則。
解:泰勒公式法(帶皮亞諾型余項)
例7(2020 年,6 分) 設f (x) ,g (x) 在x=0 的某一鄰域內有定義,對任意x ∈U,f (x) ≠g (x) , 且, 則。
方法一:利用拉格朗日中值定理求極限
解:改寫形式,再用拉格朗日中值定理設F(t)=tg(x),則分子改寫為[f (x)]g(x)-[g (x)]g(x)=F[f (x)]-F[fg(x)]
方法二:冪指函數中用等價無窮小求極限
解:[f (x)]g(x)-[g (x)]g(x)是兩個冪指函數的差,已知
例8(2021 年,14 分)設函數f (x)在閉區間[a,b]上有連續的二階導數,證明:
證明:對區間[a,b] 作等n 分,a=x0﹤x1﹤…﹤xk﹤…﹤xn=b,則各子區間[xk-1, xk]的長度都為,,k=0,1,2,…,n
因 為f (x) 在 區 間[xk-1, xk] 上 連 續,所 以 存 在 xMk,xmk∈ [xk-1, xk],由夾逼準則,得
3 結論
總結介紹極限計算的20 種解題方法在歷屆大學生數學競賽中的應用,不僅有助于學生更好地掌握極限的解題方法和技巧,也有利于提高學生分析解決問題的綜合能力,激發學生的學習興趣和發散性思維。以表格和折線圖的形式給出考察極限的屆數、題號、分值、用到的方法以及運用的次數情況、分值變化趨勢等,對指導數學競賽的指導教師和參賽學生把握極限這個內容有一定的參考價值。

