2023年新高考數學多選題題型的預測與模擬
史記祥 余繼光
(1.江蘇省泰州市姜堰第二中學;2.浙江省紹興市柯橋中學)
本文通過對過去兩年新高考數學多項選擇題的知識點梳理,總結命題特點與應試特征,得到最后階段復習的一些啟示,并結合新高考數學命題的規律進行預測,最后提供原創的數學模擬試題,拋磚引玉,以提高新高考數學復習的針對性與有效性.
多項選擇題從題干到選項圍繞一個較大主題展開,從內涵到外延,從表征到本質,從判斷到推理,覆蓋面較大,綜合性較強.多選題的構成要素較復雜,破解的難度較大,需要的能力點較多,運算,推理,應用能力都可能會觸及到,多項選擇題增加了考生數學思維的復雜性,要求考生更加細心.新高考數學命題引入多項選擇題后,在高考數學復習時應該增加相應的專題訓練.
1.2021—2022年新高考數學多選題的啟示
1.1 知識點分布
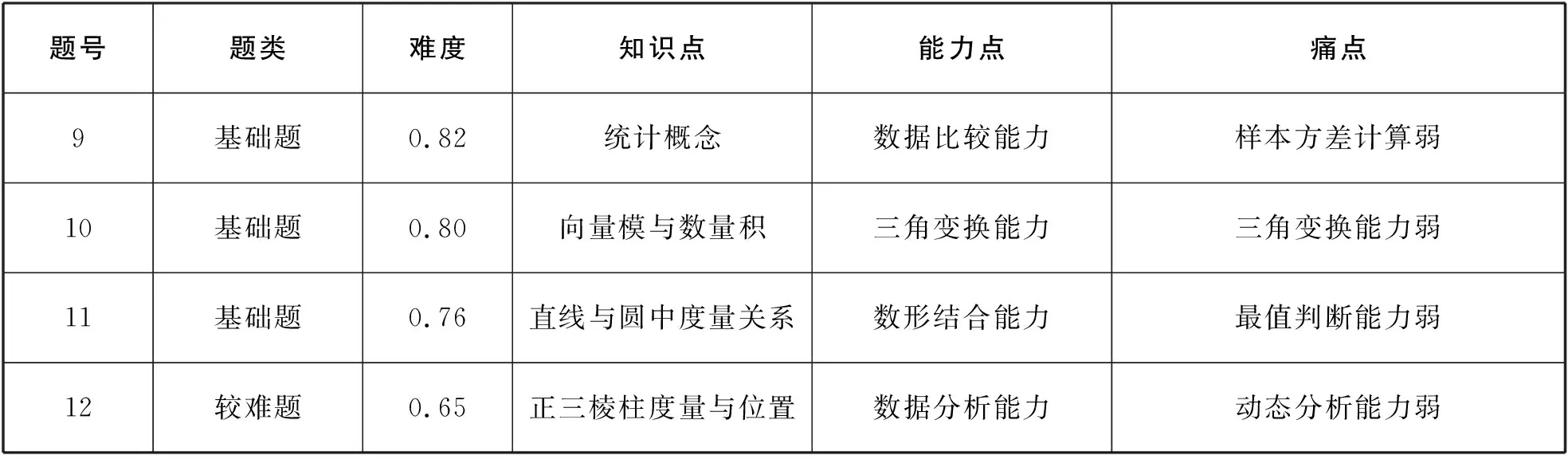
表1 2021年新高考數學多選題
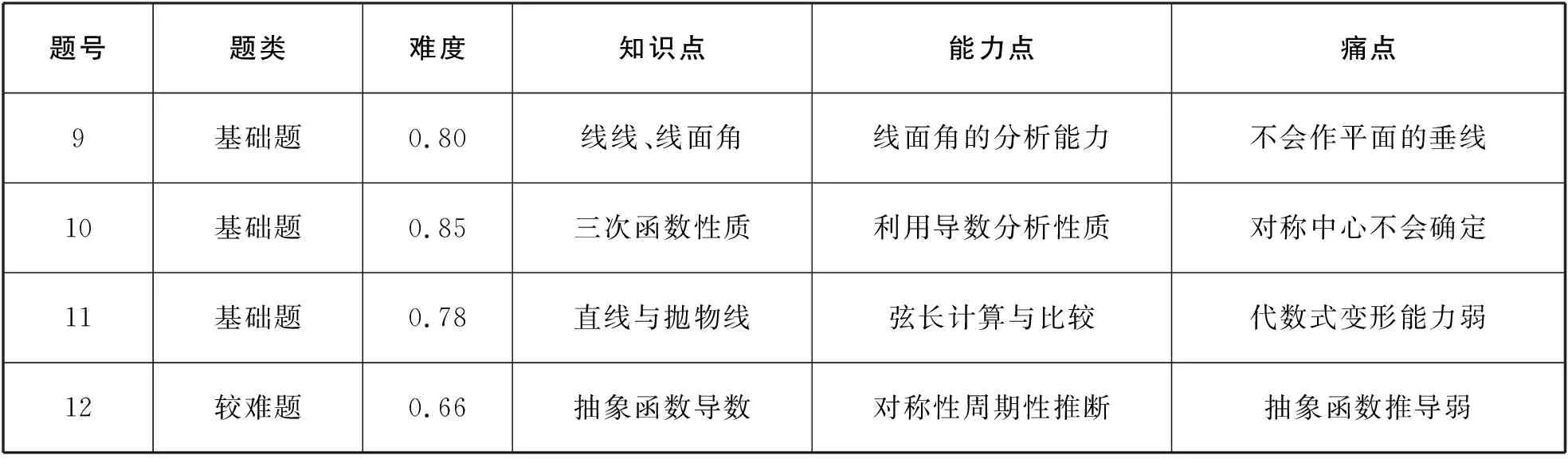
表2 2022年新高考數學多選題
1.2 多選題應試特征
從近兩年新高考數學多選題知識點角度來看,空間圖形、直線與圓錐曲線為必考點,向量、函數導數次之;從能力點角度來看,三角變換與數據分析能力要求高,運算能力次之;從痛點分布來看,多選題能力要求高,數學思維能力弱者痛點多,障礙多.
1.3 數學課堂的教學啟示
一是教學落腳點關注數學基本概念與基本方法,考生只要打好數學基本功就能獲得較好成績;
二是圍繞干擾項的類型進行復習,如條件疏漏(將容易疏漏的條件所產生的結果設計為干擾項);實際背景忽視(細心模擬學生的演算過失和差錯,得到迷惑性較強的干擾項,對提高試題的針對性和鑒別力十分有效);概念混淆(針對學生容易混淆的概念、性質設計為干擾項);題意誤解(讀題不慎,審題不細,誤解題意,由此引發的錯誤結論設計為干擾項);推理錯亂(由不合邏輯地推理而造成的錯誤結果設計為干擾項);思維定式(熟悉的內容,相似的形式,常會令人產生類比與聯想,可能產生負遷移,由此導致的錯誤設計為干擾項).
2.2023年新高考數學多選題的預測
2.1直線與圓錐曲線內容在新高考數學命題中一般都有一大(解答題)二小(客觀題),所以在多選題中必有一題,直線與圓、直線與橢圓、直線與雙曲線、直線與拋物線都有可能,而且考的比較多的是直線與圓錐曲線中的位置關系與數量關系,命題的范圍比較大,因此復習盡可能覆蓋面寬一點.
2.2空間圖形內容在新高考數學命題中一般也是一大(解答題)二小(客觀題),所以在多選題中必有一題,空間直線、平面的位置關系與度量關系都是命題的落腳點,命題的切入點傳統的是正向命題,可以嘗試的是從策略方案角度切入創新,側重于位置關系,因為解答題一般會涉及空間三大角的計算.
2.3數列是高等數學學習的基礎,雖然2021年與2022年多選題中還沒有涉及到,但是數列內容在新高考數學命題中一般會有一大(解答題)一小(客觀題),關鍵是一小放在填空還是選擇題中,數列重點在等差數列、等比數列、特殊數列,前兩項內容在解答題的可能性更大,而特殊數列選準創新點可能會對整份試卷是一大亮點.
2.4函數與導數在新高考數學命題中一般都有一大(解答題)二小(客觀題),所以在多選題中可能會有一題,其內容重點在檢測函數性質應用,導數可能會成為函數應用時的一個工具,為了將創新意識與發散性思維引入高考數學命題,命題的結構與形式會很靈活.
3.2023年新高考數學多選題的模擬
3.1 直線與圓錐曲線
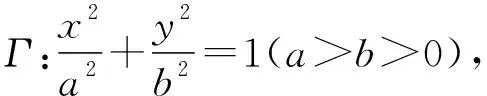
( )
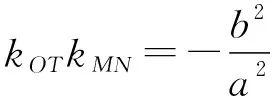
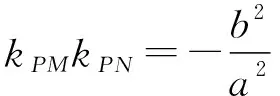
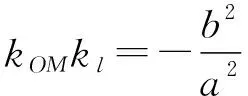
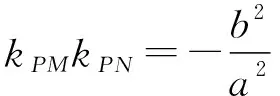
【答案】ABCD
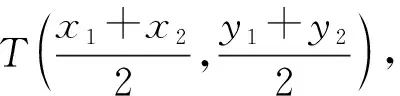
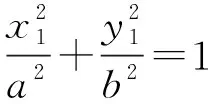
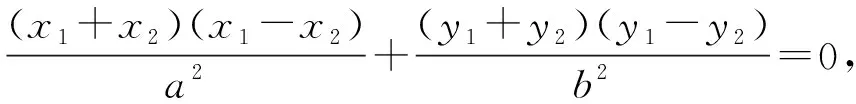
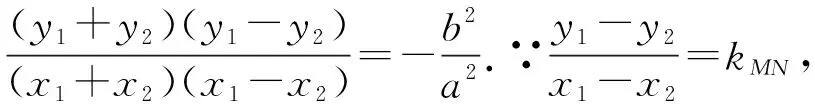
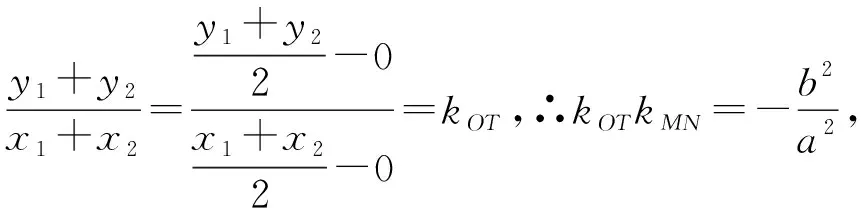
設M(x1,y1),N(-x1,-y1),P(x,y),由M,N,P在橢圓上,得
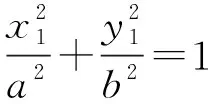
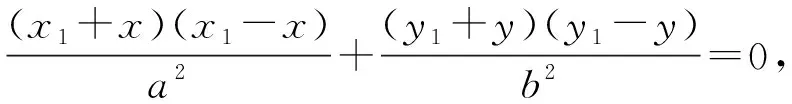
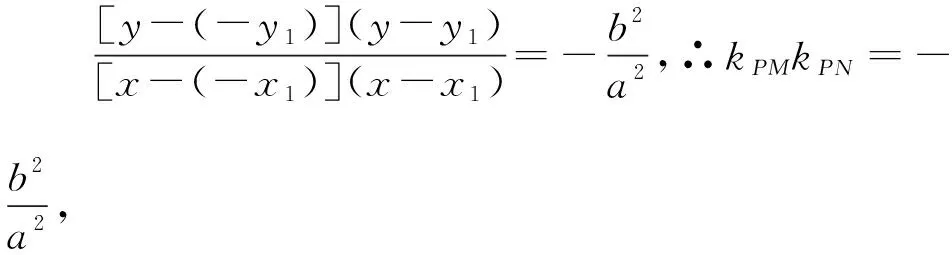
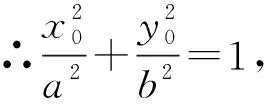
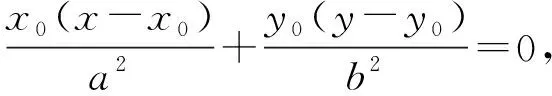
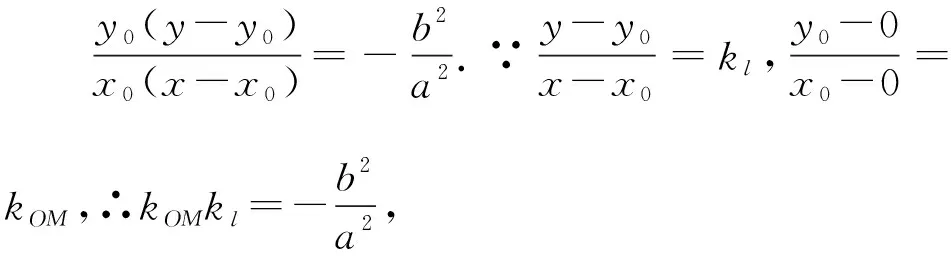
選項D是選項B的一種特殊情形,故選項D同樣正確,
故選ABCD.
【設計意圖】點差法探究發現橢圓的弦斜率與弦中點與原點連線斜率之積的數量關系規律;橢圓內兩條弦,所得到的數量規律與它是一致的;橢圓內的弦移動至相切,得到的數量規律仍不變,此問題反映直線與橢圓位置關系與度量關系中非常重要的性質,是圓錐曲線中的一個經典問題,應試中能夠檢測學生的基本功,很多學生并不知道這一經典,也沒有完全掌握點差法,可能沒有想到這4個命題都是正確的,命題本身結構簡潔整齊,體現數學美.
3.2 空間圖形
在正三棱柱A1B1C1—ABC中,D是C1C的中點,O是A1B與AB1的交點,E是OA的中點,尋找證明EC∥平面A1BD的正確途徑有
( )
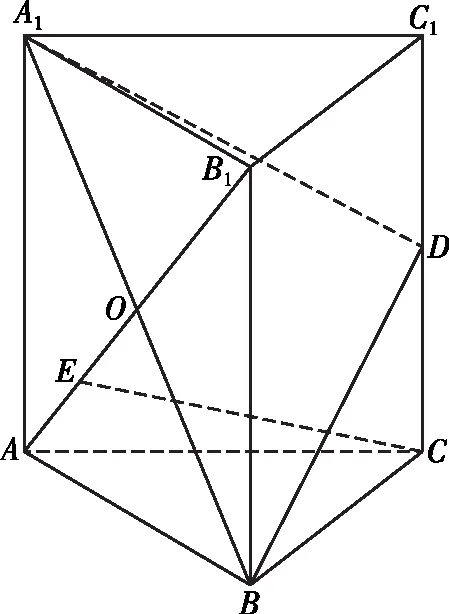
A.選取OA1的中點為F
B.選取B1C與BD的交點為R
C.選取AB的中點為G
D.選取AA1的中點為H
【答案】ABCD
【解析】對于A,如圖1,把EC沿CD方向平行投影光束到平面A1BD上,可得DF,此時點F為OA1的中點,易證四邊形CDFE為平行四邊形,得EC∥平面A1BD,故選項A正確;
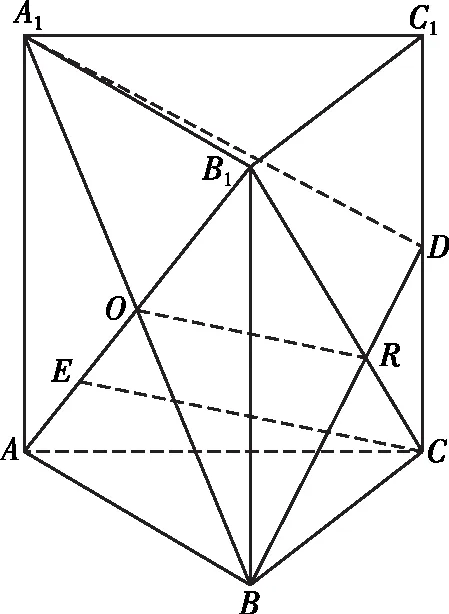
圖1
對于B,如圖2,將B1作為點光源,在平面A1BD內連接OR,其中心投影光束為EC,利用線段成比例證明OR∥EC,得EC∥平面A1BD,故選項B正確;

圖2
對于C,如圖3,把點E沿A1B方向平行投影到平面ABC上,得到點G,則由EG∥A1B,GC∥OD可證平面EGC∥平面A1BD,得EC∥平面A1BD,故選C正確;
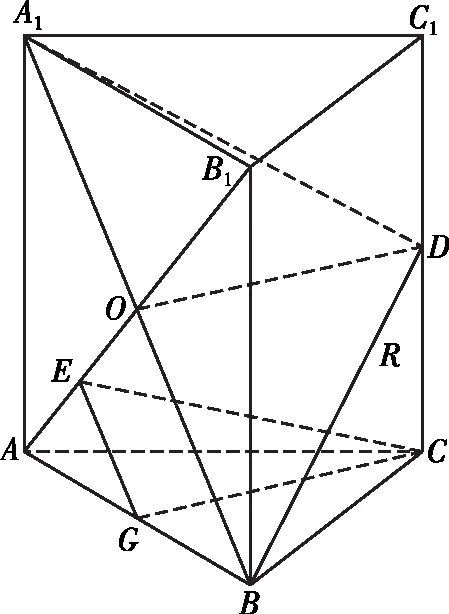
圖3
對于D,如圖4,把點E沿BA1方向平行投影到平面AA1C1C上,得到點H,H為A1A的中點,則由EH∥A1B,HC∥A1D,可證平面EHC∥平面A1BD,得EC∥平面A1BD,故選項D正確.
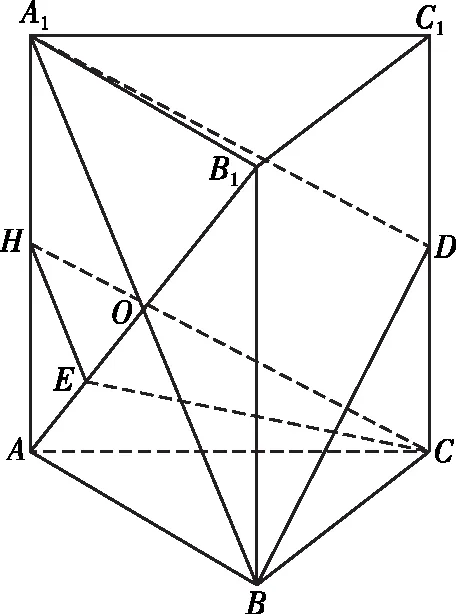
圖4
故選ABCD.
【設計意圖】尋找證明直線與平面平行的途徑,看似簡單,但需要作輔助圖形或輔助線,驗證思維途徑正確性的經驗是:尋找點或線或圖形的投影,一次次通過平移線段CE的位置來進行探索,最后通過邏輯推理完成問題,命題本身語言簡潔,命題角度新穎,從邏輯思維的角度來檢測學生的數學思維,思維量大,沒有運算量,從解題策略與方案優化上命題將是新高考數學命題的一個方向,此命題思路也可以用在證明直線與平面垂直、平面與平面垂直的策略與途徑上,提升思維難度.
3.3 特殊數列
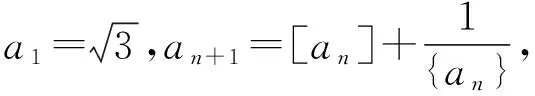
( )
【答案】ABCD

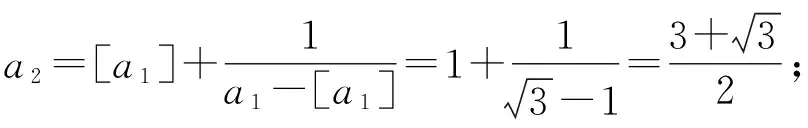
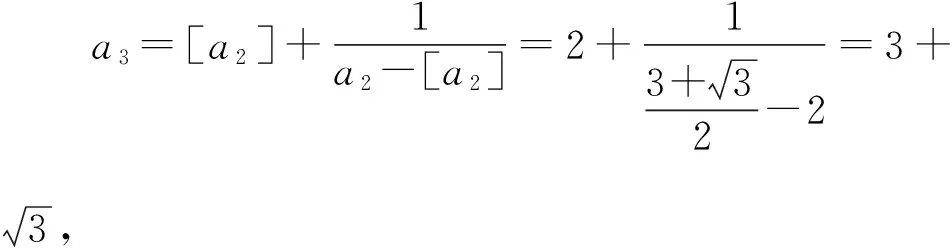
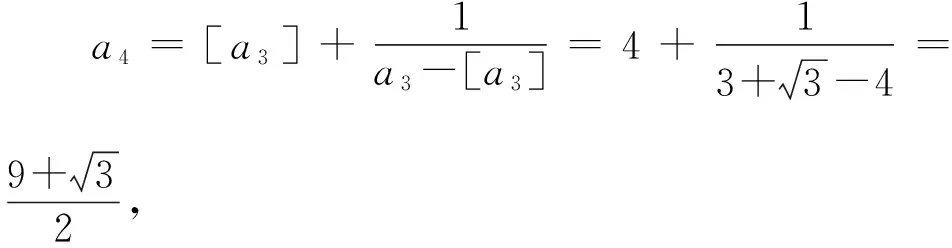
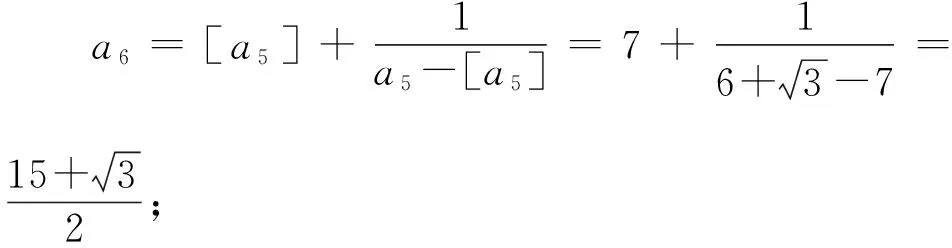
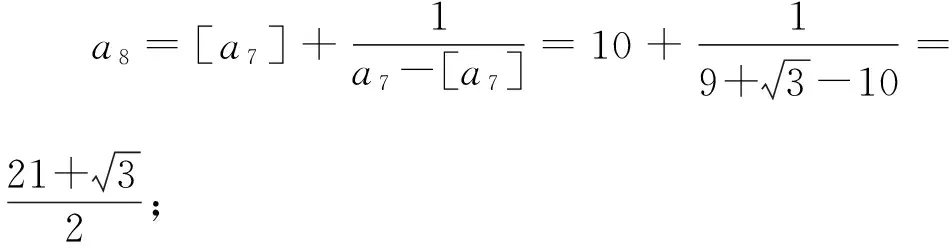
得到下標規律如表所示:

下標(n為奇數項)1357…2n-1an3×0+33×1+33×2+33×3+3…3×(n-1)+3規律3×(1-1)+33×(2-1)+33×(3-1)+33×(4-1)+3…3×(n-1)+3
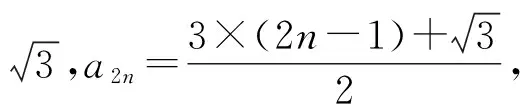
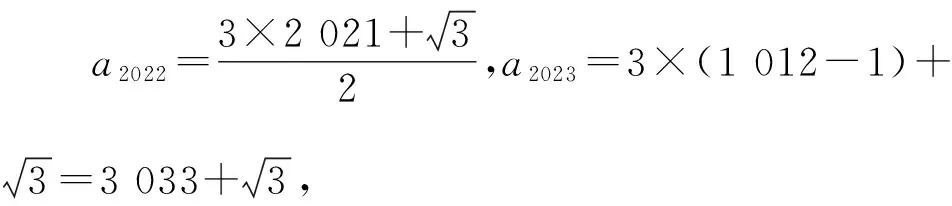
故選ABCD.
證明:當n=1時,命題顯然成立.
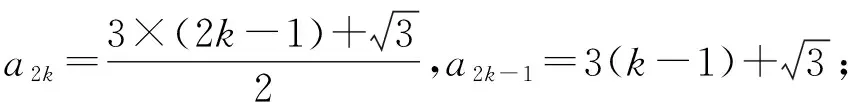
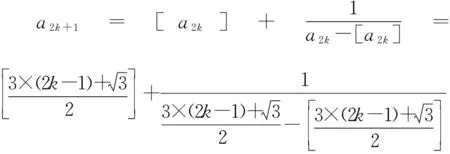
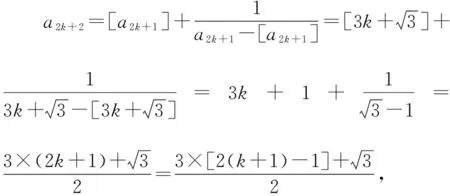
命題也成立,根據數學歸納原理,對任意正整數n,命題都成立.
【設計意圖】遞推思想與遞推能力不僅是數列的重要思想方法,也是科學研究的基本功,取整函數與小數函數雖然在中學數學中使用率較小,但在高等數學中起著十分重要的作用,特殊數列的規律不是十分明顯,必須通過遞推去發現、去歸納、去猜測,由特殊到一般尋找下標規律比較困難,所以此題的難度較大.
3.4 函數導數
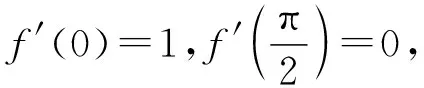
( )
A.學生甲構造函數f(x)=asinx舉一例為f(x)=sinx
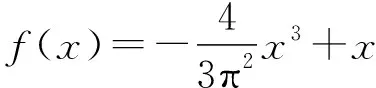
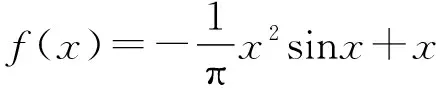
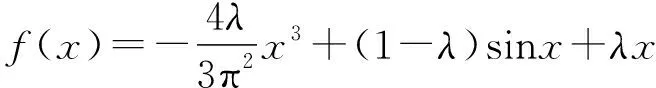
【答案】ABCD
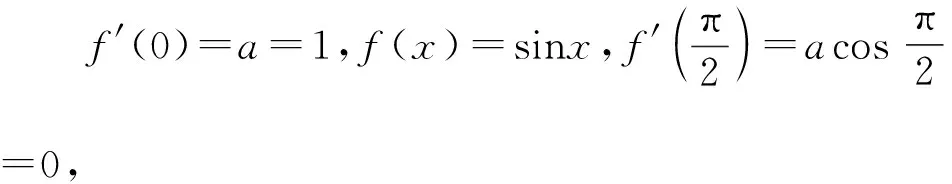
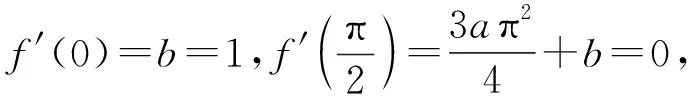
f(x)=ax2sinx+bx,f′(x)=(2axsinx+ax2cosx)+b,為偶函數,f′(0)=b=1,
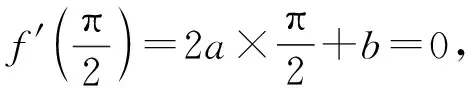
f(x)=ax3+bsinx+cx,f′(x)=3ax2+bcosx+c,f′(0)=b+c=1,
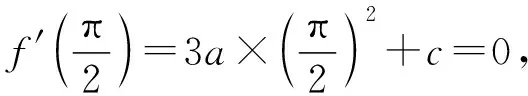
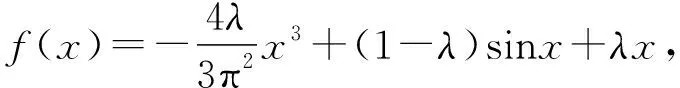
故選ABCD.


