一種求解番茄種植規劃問題的多目標粒子群-生物地理學優化算法

羅 丹 蔣兵兵

1(湖南鐵道職業技術學院軌道交通智能控制學院 湖南 株洲 412000) 2(湖南鐵路科技職業技術學院鐵道供電與電氣學院 湖南 株洲 412000)

0 引 言

番茄作為一個重要農作物,年平均種植面積在70 000公頃以上,占我國產量的90%左右,其出口量占全球貿易量的1/4[1]。在番茄加工期,在番茄生產能力與加工廠的加工能力之間存在嚴重的不平衡。主要表現在番茄采摘季的前后期,由于番茄的產量偏少,造成加工生產線的閑置,使得醬廠的生產效率降低;而在番茄采摘季的中期,番茄的產量明顯偏高超過醬廠的加工能力,造成加工番茄的堆積和變質以致浪費,使得番茄醬的質量下降。在加工期番茄原料的供應不均衡,容易給農戶和企業造成較大的經濟損失,同時也給環境造成一定的污染。因此,番茄種植規劃問題的研究能夠為番茄醬加工企業以及番茄種植戶提供種植規劃方面的理論指導,并產生一定的實際實用價值[2-3]。

在許多發展中國家,農作物的種植規劃正在成為研究的熱點,且越來越多的學者將各種智能優化算法逐漸應用到種植規劃中。生物地理學算法[4](Biogeography-based Optimization,BBO)是一種繼蟻群算法、細菌覓食算法和螢火蟲算法之后的又一個熱門研究算法。該算法被測試在一些性能上表現得比傳統智能優化算法更好,已被成功地應用到經濟負荷調度、旅行商問題和機器人路徑規劃等實際問題中。

本文旨在將具有快速收斂性能的粒子群算法與收斂速率不足的生物地理學算法相結合,采用“取長補短”的方式,結合兩種算法的優勢,提出一種基于粒子群優化的改進生物地理學算法,將該算法在NSGA-Ⅱ中的快速非支配排序法基礎上進行優化,形成基于非支配排序的多目標粒子群-生物地理學算法(Nondominated sorting Biogeography-based Optimization with Particle Swarm Optimization, NSPBO),用于對構建的多目標番茄種植規劃模型進行求解,以期能夠協調各目標之間的關系,獲得最合理的種植規劃方案。

1 多目標番茄規劃模型的構建

以新疆吉木薩爾縣某番茄醬加工廠(企業)的環境參數為例進行多目標番茄規劃模型的建立。本研究主要考慮三個目標的綜合優化:在滿足工藝約束的情況下,一是使得企業經濟損失最小,即使番茄產量達到供應平衡;二是使得種植戶總凈收益最大,即種植戶能夠利用有限的土地獲得盡可能多的收益;三是使得土地利用率最大,即在滿足約束的前提下使十個品種的番茄種植面積最小。

1.1 三個目標函數

(1)目標函數1:企業經濟損失最小。

為了使經濟損失最小、原料浪費最少和生產效率最高,應使番茄日產量與加工廠日產能的誤差的平方和最小:

(1)

式中:D為番茄醬廠的總加工時間;EY為醬廠所有生產線日加工產量;PYj為估計的第j批(即第j天種植的)番茄產量。

(2)

式中:N為種植番茄的品種數目。每個品種的番茄產量Y的向量模型表達式為[15]:

(3)

式中:Yj(i)為第j批(即第j天種植的)i號番茄的實際產量,單位(kg);Y0j(i)為第j批i號番茄的單位面積基本產量;Aj(i)為第j批i號番茄的種植面積,單位m2;S(k)為第k天的光照強度;T(k)為第k天的平均積溫;N(k)為第k天的土壤營養狀況;W(k)為第k天的土壤水分狀況;P(k)為第k天的病蟲害狀況;Mj(i)為第j批(即第j天種植的)i號番茄的實際生長期;M0j(i)為第j批i號番茄的基本生長期;Bpy、Bny、Bty、Bwy和Bsy分別為反映番茄在生長過程中受病蟲害、土壤營養、積溫、土壤水分和光照強度對農作物產量的影響程度;Bsh和Bth分別為反映在生長過程中光照和環境積溫對加工番茄生長的影響程度。

(2) 目標函數2:種植戶總凈收益最大。為使種植戶的凈收益最大化:

(Aj(i)×WRi×WC)]-FARM

(4)

式中:Ci為第i號番茄的總收益/kg;WRi為第i號番茄用水量/m2;WC為水價/m2;FARM為種植戶總的成本。

(3) 目標函數3:土地利用率最大化。即面積最小:

(5)

1.2 目標函數的約束條件

(1) 約束條件1:總的種植面積。

種植規劃方案中,番茄醬廠需要的種植面積不能超過所有種植戶的總面積。因此,十個品種的番茄的總的種植面積應該小于或者等于總面積。

(6)

式中:TPA為番茄醬廠的總種植面積/m2。

(2) 約束條件2:種植面積的地塊信息。番茄醬廠的種植面積是由許多獨立地塊組成,在減少種植時對面積的計算將獨立地塊不再劃分,即每塊地在一天內只能種植一個品種且地塊面積必須全部種植。

Aj(i)=LAND

(7)

式中:LAND為番茄醬廠的地塊信息。

(3) 約束條件3:固形物含量SC。滿足基本要求:

SC(x)≥BSC

(8)

式中:BSC為原料中SC要求的最低含量,單位mg/g。

(4) 約束條件4:番茄紅色素含量HC。滿足基本要求:

HC(x)≥BHC

(9)

式中:BHC為原料中HC要求的最低含量,單位mg/100 g。

(5) 約束條件5:維生素含量。番茄加工對維生素VC含量不得低于基本要求。

VC(x)≥BVC

(10)

式中:BVC為原料中VC要求的最低含量,單位mg/100 g。

1.3 番茄規劃的數學模型

根據上述分析得到約束條件的番茄規劃數學模型,直接求解過程會非常復雜。本文根據罰函數法,即將表示企業損失最小的目標表達式F1進行增廣,將其轉化為無約束數學模型,得到新的F1函數,其數學表達式為:

F1(X,Mk)=min{f1(X)+M1×

max(SC(x)-BSC,0)+M3×max(HC(x)-

BHC,0)+M4×max(HC(x)-BHC,0)}

(11)

式中:M1、M2、M3和M4分別表示懲罰因子。

有上述的描述可以得到為番茄規劃的數學模型:

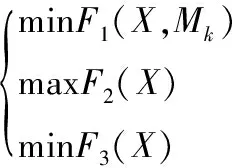
(12)

2 求解番茄種植規劃的NSPBO

2.1 粒子群優化

在標準粒子群優化算法(PSO)中,可用字母變量Xi表示第i個粒子,變量Vi表示其對應的速度,將其每次迭代中獲得的最優個體位置(局部極值)表示為Pi,其中整個迭代過程中的最優個體位置(全局極值)表示為Pg。則粒子的速度和位置更新公式為:

Vi(t+1)=γ(Vi(t)+c1·r1(Pi(t)-Xi(t))+

c2·r2(Pg(t)-Xi(t)))

(13)

Xi(t+1)=Xi(t)+Vi(t+1)

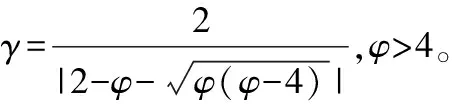
2.2 生物地理學算法

在BBO中,問題的每個解對應每個番茄品種每批的種植面積被稱為一個適宜度指數變量(SIV)。每個解的度量函數值對應每個種植方案的目標函數值被稱為一個適宜度指數(HSI)。生物地理學算法的基本介紹參考文獻[5-6]。BBO的兩個操作算子簡述如下:

(1) 棲息地的遷移操作[7-8]。

根據λi選擇需要遷入的棲息地Xi,確定Xi后;根據μj選擇需要遷出的棲息地Xj,并隨機選擇一個棲息地Xm;然后從Xj和Xm中分別選擇SIV進行混合替代Xi中相應SIV。

(14)

式中:α為加權因子,rrand為隨機數,rrand∈(0,1)。

(2) 棲息地的突變操作[9-10]。突變操作中發生突變的概率計算公式:

(15)

式中:Mmax為最大突變率,Pmax=arg(max(Ps)),s=1,2,…,Smax。然后根據Ms選擇需要突變的棲息地,隨機選擇該棲息地的一個SIV將其用按高斯分布隨機生成的一個量替代[10]。

2.3 NSPBO

BBO算法的收斂速率及精度差但探索能力強[11]。PSO的速度及位置更新操作可以使得粒子的搜索范圍變得愈來愈窄,同時不斷地向最優解靠近,雖然在迭代前期算法收斂很快,但是到后期由于搜索區間的局限性使得粒子可能無法跳出局部極值,這就造成了粒子的搜索能力被大大減弱。為了充分地利用每個操作算子,將PSO的速度及位置更新方式與BBO的操作算子合理地相結合形成一種改進算法,簡稱PSOBBO。其中,BBO每個棲息地信息與PSO的每個粒子位置信息互相對應。

受NSGA-Ⅱ算法的設計原理啟發,將快速非支配排序法與本文算法聯合起來,并用于解決多目標番茄種植規劃等實際問題。將快速非支配排序法與PSOBBO相融合[12],用 PSOBBO的位置和速度更新操作、遷移和突變操作機制代替NSGA-Ⅱ算法的GA的選擇、交叉、變異操作機制,以用于求解具有多目標的番茄種植規劃模型。文中將采用非支配排序的PSOBBO稱為多目標粒子群生物地理學算法(NSPBO)。NSPBO的具體工作步驟如下:

(1) 參數初始化,包括BBO的參數及PSO的參數c1、c2和φ;隨機生成任一棲息地信息X(t0),即算法中的棲息地向量與優化問題的種植方案一一對應。

(2) 根據目標函數計算每個棲息地的適宜度函數值f(X),按降序排序;保存本次的最優適宜度函數值為pbest,獲得pbest的棲息地信息為局部最優個體Pi;保存整個算法運行中的最優適宜度值為gbest,對應的棲息地信息為全局最優個體Pg。

(3) 根據第(2)步的計算方式更新適宜度函數值得到新的f(X),并按降序排列,獲得對應棲息地的物種數目Si,根據余弦遷移模型計算遷入率λ以及遷出率μ,并保存最優解。

(4) 根據文中給出的干擾遷移操作算子式(14)獲得新的棲息地信息U(t)和新的適應度值f(U)。

(5) 根據高斯變異操作選取需要進行突變的棲息地完成變異,并修改對應的棲息地信息V(t),重新計算適應度值f(V)。

(6) 比較棲息地信息。若f(X)比f(V)和f(U)更優,則棲息地信息X(t)不變,若f(V)或f(U)比f(X)更優,則棲息地信息X(t)用U(t)或V(t)替換。

(7) 根據PSO算法的信息更新公式獲得新的棲息地信息,并對pbest、Pi和gbest、Pg進行更新。

(8) 根據參考文獻[12]的計算方式對獲得的解集計算極大極小距離密度,進行快速非支配排序。

(9) 判斷是不是到達最大迭代次數Tmax。如不滿足,則t=t+1,轉到步驟(3);否則輸出優化過程中保存的最優解gbest。

(10) 根據實際需求,從Pareto最優解集中選取最合理的番茄規劃方案。

2.4 性能比較

為了驗證NSPBO應用于番茄規劃問題求解的有效可行性,先選取常用的二維函數進行測試,ZDT系列中的ZDT1、ZDT3,再選取三維函數進行測試DTLZ系列中的DTLZ1、DTLZ2進行性能驗證。

NSPBO算法的環境參數設置如下:最大遷入和遷出率E=I=1.0、Mmax=0.1、c1和c2均為2.0、γ為1.0;不同測試函數的兩個相關環境參數NP和Tmax設置詳見表1,其他算法也是相同的設置。NSPBO算法獲得的Pareto前沿如圖1所示。

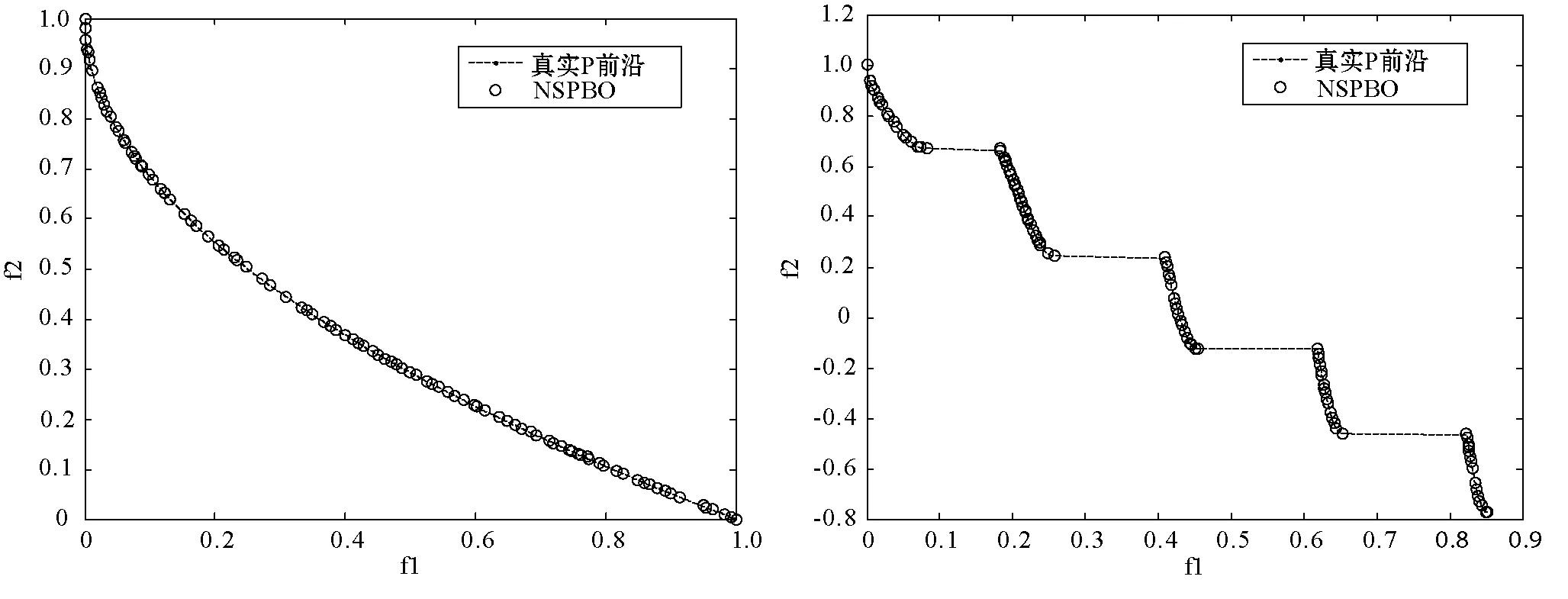
(a) ZDT1 (b)ZDT3

表1 環境參數設置

由圖1、表2和表3測試結果可以看出,本文算法在二維函數的測試上可以將解集收斂到最優,針對具有一定難度的三維函數,NSPBO也能夠收斂到已知的Pareto前沿解集,Pareto前端不論是具有非連續的ZDT3函數還是凸的三維函數DTLZ系列,測試結果表明本文算法NSPBO都可以收斂到圖中的真正Pareto前端上,同時獲得的Pareto前端在分布性上表現較均勻,表明提出的算法是合理和可行的。

表3 四種算法獲得的SP的平均值及方差

為了進一步驗證NSPBO的有效性,與NSGA-Ⅱ[12]、NSPSO[13]、NSBBO[14]進行比較,各算法實驗的參數設置參考文獻[12-14]中的設置,NSGA-Ⅱ算法的交叉因子為0.9、變異因子為0.01,交叉和變異分布參數均為15;NSPSO算法的c1和c2均為2.0,γ為1.0。采用文獻[15]中的世代距離GD和分布性評價指標SP分析MDBBO的有效性,其中GD和SP的兩個評價指標分別表示收斂到Pareto前端的性能和獲得的Pareto前端在空間分布的均勻程度,其值均是越小越好。通過MATLAB 2010b軟件仿真,將四種每個算法分別獨立運行20次,經計算獲得的GD和SP平均值及方差的數據對比如表2所示,表2中用字母A、B、C、D分別表示代替NSPBO、NSGA-Ⅱ算法、NSPSO、NSBBO。

對表2數據進行對比分析可以看出,對于四個測試函數,NSPSO和NSPBO的收斂性指標GD值都比較近似,但從二維函數ZDT1、三維函數DTLZ1和DTLZ2的測試數據來看,NSPBO的GD值是四種算法中數值最小的,NSPBO獲得的數據結果要優于NSPSO,同時NSPBO對三維測試函數DTLZ1、DTLZ2在收斂性上比另外三種算法表現更好。從表3可以看出,對四個測試函數得到的SP值,NSPBO的均值均是最小,表明NSPBO的均勻分布性要優于其他三種算法,同時也表明NSPBO在多目標優化問題上是有效的。

3 仿真與分析

新疆某地區某番茄醬廠提供的部分環境參數為:D為60 d;EY為3 000 000 kg/d;TPA和LAND值由某工廠提供;番茄品種的參數信息參考文獻[15-16],部分參數如表4所示;醬廠對番茄原料中的固形物、紅色素和維生素含量分別為12.16 mg/100 g、5.6 mg/100 g和5.6 mg/100 g。

表4 番茄品種的參數信息

本文將所提出的NSPBO與NSPSO、NSGA-Ⅱ 、NSBBO分別對多目標番茄規劃模型進行求解,以此測試和驗證算法的可行性和有效性。使用MATLAB 2010b 軟件仿真,文中四種算法得到的番茄種植規劃問題的Pareto最優前沿曲線圖和極端解的數據表分別如圖2和表5所示。在每個地塊的面積是固定的情況下,由于地塊的信息中難免有面積一樣的,所以在選擇地塊的時候存在多解。

(a) NSGA-Ⅱ算法 (b) NSBBO

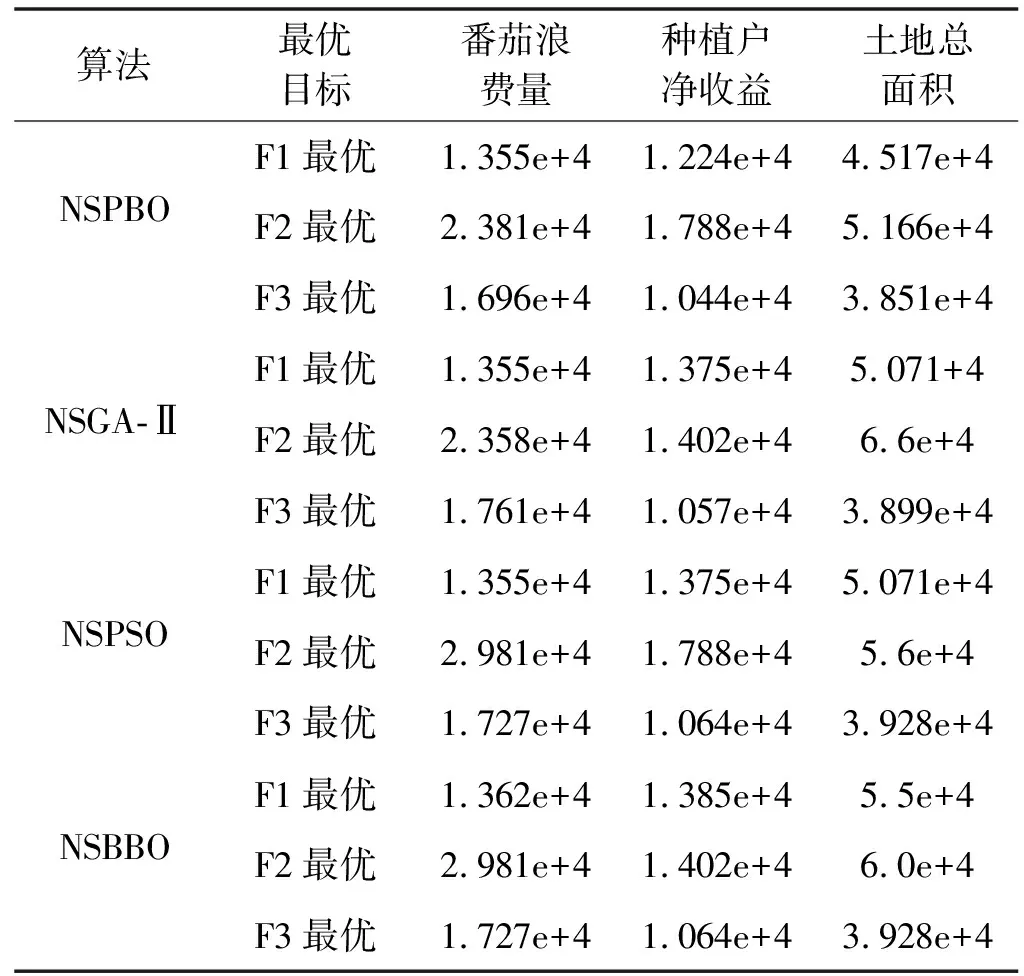
表5 四種算法獲得番茄種植規劃問題的極端解

由圖2(a)可以看出,隨著土地面積的增加,番茄種植戶總收益不增加,而番茄浪費量即企業利潤的損失不斷增加,因此,NSGA-Ⅱ算法較其他算法得到的Pareto最優前沿在空間分布上比較局限,解集的完整性表現最差。而由圖2(d)可以看到,在分布長度的完整性上,獲得的整個Pareto前端要明顯優于圖1(a)和圖1(c),因此,NSPBO的完整性表現較好;從空間分布上看,圖2(d)的解集在整個Pareto前沿的空間分布上表現得更加均勻,要優于圖2(b)和圖2(a)。

同時從表5可以看出,在F1最優的極端解情況下(即番茄浪費量最少),NSPBO和NSGA-Ⅱ、NSPSO在三個優化目標上都能夠獲得相同的極端解,表明在考慮番茄浪費率上都可以獲得最優的番茄種植規劃。在F2最優的極端解情況下,NSPBO和NSPSO都能夠保障種植戶獲得最大凈收入,但NSPBO相比NSPSO雖然在番茄浪費量上增加0.975%,但NSPSO種植面積上比NSPBO要增加8.40%,在這種情況下NSPBO獲得種植方案更加合適。在F3最優的極端解情況下,各算法獲得種植面積極端解都是比較接近的,但NSPBO在番茄浪費量和種植戶收益優化效果更好,在考慮種植面積最優時,NSPBO獲得種植方案要優其他幾種算法。

因此,本文算法與NSPSO、NSGA-Ⅱ和NSBBO進行比較,采用本文算法獲得的Pareto前沿在完整性和分布均勻性上都要表現得更加突出。綜上所述,提出的NSPBO有更好的優化能力,能夠更好地為企業提供適合的番茄種植規劃方案。

4 結 語

番茄醬原料存在長期供應不均衡的情況,而這一現象與番茄種植的規劃相關,因此本文通過對番茄種植規劃進行數學模型,然后應用 NSPBO求解多目標番茄規劃模型,其中番茄規劃模型綜合考慮了經濟因素和環境因素。該算法有機融合了 Pareto 快速非支配排序法和粒子群速度位置更新操作與生物地理學算法遷移和突變操作,增強了算法對多目標問題的優化能力。通過實際案例分析,該方法算法能夠有效地為企業和種植戶提供某一目標優化偏好的種植規劃方案,并與NSPSO、NSGA-Ⅱ和NSBBO進行比較,本文算法NSPBO 的 Pareto 前沿無論在目標空間的分布上還是解集的完整性上都具有更好的表現,能夠更好地實現任一目標偏好。因此,本文算法能夠為多目標番茄種植規劃的求解提供適合的種植規劃方案。