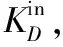基于改進K-Shell的社會網絡關鍵節點挖掘算法

李蜜佳 衛紅權 李英樂 劉樹新

(中國人民解放軍戰略支援部隊信息工程大學 河南 鄭州 450001)

0 引 言

對復雜網絡進行深度挖掘和分析在理論和現實中具有重要意義[1]。社會網絡是復雜網絡的一個領域,包括人際關系網、Twitter網和論文合著網等。社會網絡中的各個節點,由于在網絡中的結構地位以及活躍度的不同,所起的作用也不同,其中有一部分節點對網絡局部或者全局影響較大,這類節點就叫做關鍵節點。通過挖掘社會網絡中的關鍵節點,可以滿足我們的很多實際需求。比如在產品推銷網絡中,商家可以消耗最少的資源實現產品最高效的推廣;在輿論傳播網絡中,政府可以使用最少的干預手段去宣傳輿論或者禁止謠言;在犯罪嫌疑人關系網絡中,警察可以快速鎖定團伙頭目,進而集中警力抓捕。

目前,在關鍵節點挖掘方面,研究人員已經從不同的角度探索了很多算法。在基于鄰居節點中心性的方法中,度中心性的方法用節點的鄰居節點數量來衡量節點重要性,計算復雜度低,但是僅考慮了節點局部重要性,沒有考慮節點的網絡位置及其他全局信息,準確性不高。Chen等[2]提出了一種半局部中心性方法,該方法只統計節點的四層鄰居的信息,比局部中心性的方法更準確且計算復雜度低,適合于大規模網絡,但是由于該方法沒有考慮鄰居節點所處的不同層次,影響了關鍵節點挖掘的準確性。之后,Chen等[3]綜合考慮了度中心性與聚集系數,又提出ClusterRank中心性,該方法適用于大規模網絡,但把網絡視為無向的,與多數現實情況不符。趙曉暉[4]綜合考慮節點的半局部中心性和聚類系數,提出了一種歸一化的局部中心性節點影響力度量算法。Kitsak等[5]認為節點距離網絡核心越近,所產生的影響力也就越大,由此提出K-Shell分解法,該方法計算復雜度低,在分析大規模網絡方面應用較多,但是僅對節點進行粗粒度劃分,準確性不高。對此,嚴沛[6]在K-Shell的基礎上,使用雙向搜索樹方法提高算法準確性。

在基于路徑中心性的方法中,Hage等[7]認為節點的影響力與節點到其他節點的距離有關,提出離心中心性,該算法很容易受到特殊值的影響。Freeman[8]提出接近中心性(Closeness Centrality),節點的緊密度越大,越靠近網絡中心,也就越重要。Freeman[9]提出介數中心性(Betweenness Centrality),將節點的重要性由通過該節點的最短路徑數目來表示,這兩種算法準確度高但計算復雜度也高。與介數中心性僅考慮最短路徑不同,Katz中心性[10]考慮節點對之間的所有路徑,并根據路徑長度對路徑加權,這種算法的時間復雜度也比較高。

在基于特征向量的方法中,Bonacich[10]提出特征向量中心性(Eigenvector Centrality),認為一個節點的重要性要綜合考慮其鄰居節點的數量和質量。Poulin等[11]假設每個節點都在社會網絡中被提名,節點的重要性與節點本身及其鄰居節點被提名次數有關,由此提出一種累計提名中心性(Cumulative Nomination Centrality),該算法比特征向量中心性收斂要快。Google引擎使用的PageRank算法[12]是特征向量中心性的變體,該算法綜合考慮指向該節點的鄰居節點數目和鄰居節點自身的重要性。Lü等[13]提出LeaderRank方法,引入背景節點使原網絡變為強連通網絡,從而替代了PageRank算法中的跳轉概率c,性能較PageRank有較大提升。

基于路徑和特征向量中心性的關鍵節點挖掘算法雖然準確度高,但是普遍時間復雜度高,無法在大規模網絡上進行應用;度中心性、K-Shell分解法等時間復雜度低的算法雖然適用于大型網絡,但是其準確度又不理想,其劃分結果難以滿足精細化節點重要性劃分的實際需求。

基于此,本文對K-Shell分解法進行改進,在分解過程中綜合考慮節點的度數與節點被刪除時所處的迭代層次,以解決K-Shell劃分結果粗粒化的問題。隨后采用一種用微觀結構去替代原有完整網絡的算法,根據改進的K-Shell節點排名提取核心網絡,并結合PageRank值對核心網絡中所有節點做定量分析,找出影響較大的節點,最終形成分層次的重要節點劃分。在三個實際網絡中進行實驗驗證,結果表明本文方法具有較低的時間復雜度,計算結果也更準確。

1 算法設計

圖G的鄰接矩陣A=(aij)N×N,A=(aij)N×N是一個N階方陣,其中:

式中:aij為節點i與j連接。

1.1 K-Shell分解法

Kitsak等[5]指出在度量節點重要性時,需要考慮節點在整個網絡中的位置,他們認為處在網絡核心位置的節點會產生較大的影響力,并提出了K-Shell分解法。

例如,圖1是一個由15個節點和19條邊組成的無權無向網絡圖。

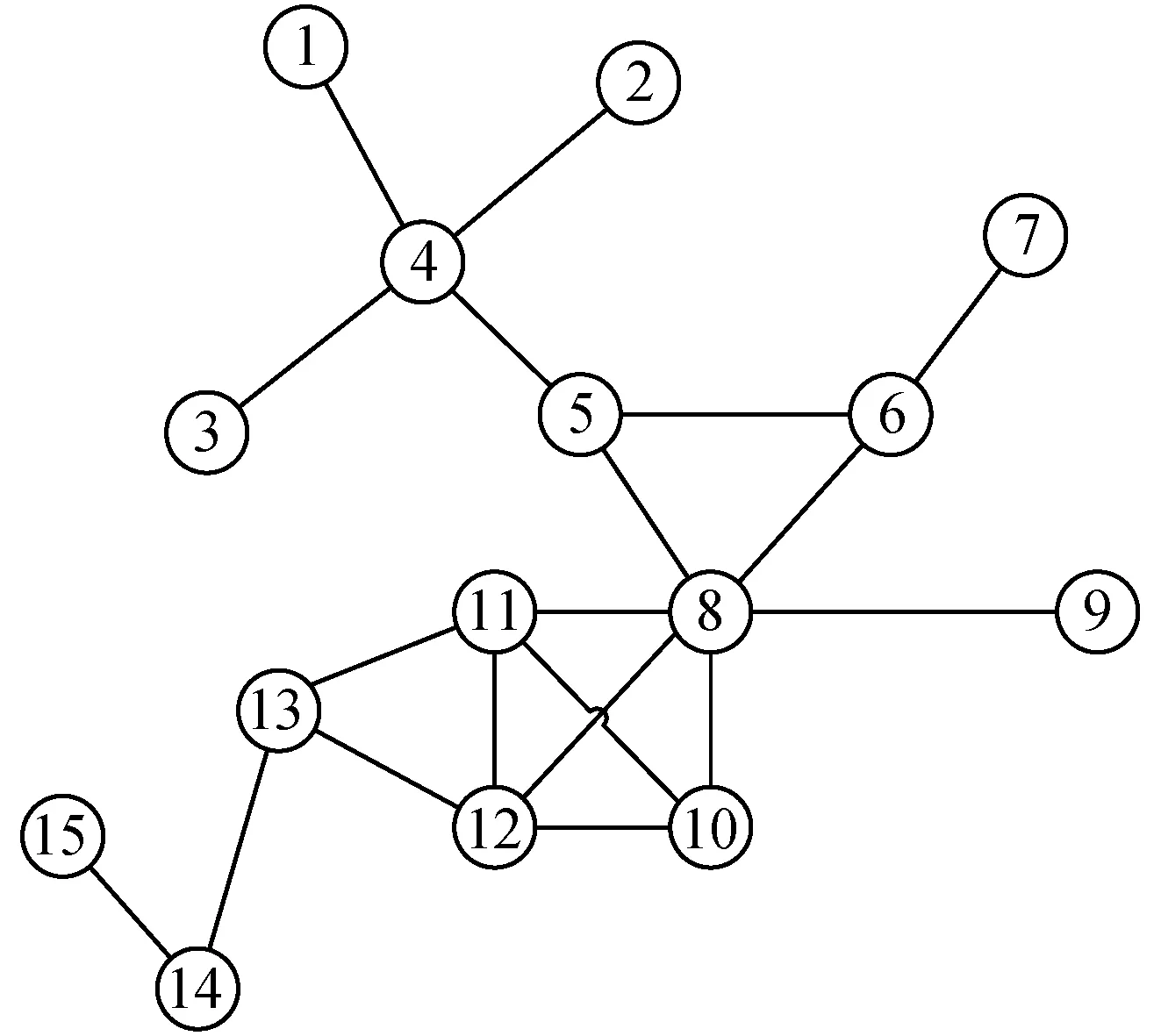
圖1 無向網絡

針對圖1所示的無向網絡,具體分解過程如下:刪除網絡中所有度為1的節點及連邊,記迭代層數為1。觀察剩余網絡中是否仍有度為1的節點,如果有,刪除節點及連邊,迭代層數記作2。循環去除,直至網絡中沒有度為1的節點,此時將所有被刪除節點K-Shell值記作1。依次迭代,刪除網絡中度為2、3、4、5、…的節點,直至所有節點都被刪除。圖2為按照K-Shell分解法對網絡中所有節點的劃分結果。

圖2 K-Shell分解

圖3 SIR模型狀態轉移

對圖1網絡記錄K-Shell分解全過程如表1所示。

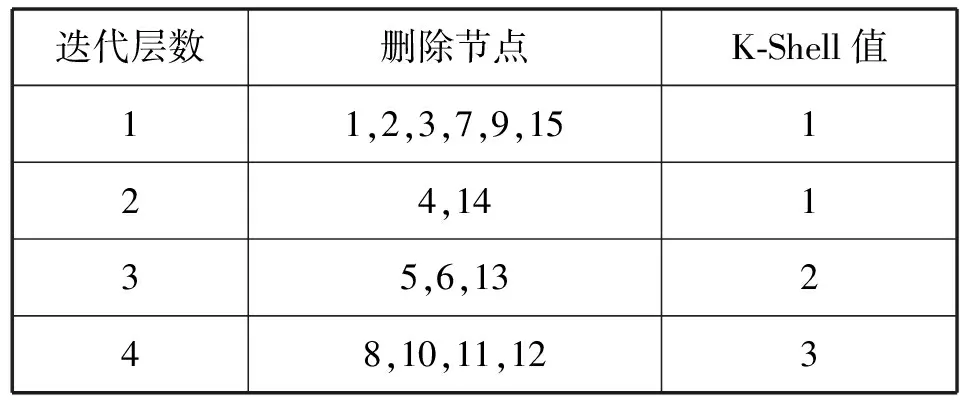
表1 K-Shell分解過程

1.2 改進的K-Shell分解法

K-Shell方法計算復雜度低,在分析大規模網絡方面應用較多,但也存在不足。第一,K-Shell分解法不區分入度與出度,而社交網絡基本都屬于有向網絡[14],節點受關注的程度由節點的入度表示,節點的合群程度由出度表示,忽略入度與出度的不同,會使一些節點以較小的代價通過建立與核心位置節點的單向連邊來提高自身核數,從而導致挖掘結果出現較大偏差。第二,K-Shell分解法屬于粗粒度劃分,把屬于同一層的節點都看作同等地位,忽略了節點度和節點被刪除時所處迭代層數的影響,導致大量節點被劃分到同一層。如在圖2的網絡中,節點1和節點4被K-Shell分解法劃分到同一層,K-Shell值相同,但顯然節點4比節點1重要。

對此,本文對算法作如下改進:

(1) 針對社交網絡多為有向網絡的特點,將傳統的K-Shell在分解過程中不區分節點入度出度的做法,改為僅考慮入度對節點進行剝離。

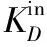
詳細分解步驟為:

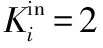
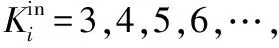
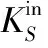
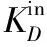
偽代碼如下:

輸入:nodes list V,Links list B。

Ks=1;

n=1;

while(|V|≠0)

add removal node i into set Vk-core(n);

add removal node i into set Vk-core(Ks);

end while

delete node i and related links;

update V and E;

n++;

end while

core++;

end while

1.3 inKD-Pr算法

PageRank算法[12]是谷歌搜索引擎的核心算法。它認為一個節點的重要性取決于指向它的節點的數目和質量。該算法作為有向網絡節點排序最經典的算法,被廣泛應用于對網頁的排序、對社交網絡上用戶的排序等。作為全局性算法,PageRank計算結果較準確,但時間復雜度高于K-Shell分解法。由于兩種算法相關性不大,本文綜合了兩種算法的優勢,構建關鍵節點挖掘模型的步驟如下:

(1) 根據社會網絡相關數據,構建鄰接矩陣。

(2) 用改進的K-Shell分解法對網絡所有節點快速打分。

(3) 按照得分高低,依次刪除外圍大約80%的不重要的節點及其連邊,減小網絡規模。

(4) 對步驟(3)中提取的核心網絡,運用PageRank算法計算出每個節點的p值,并進行歸一化和無量綱化處理。

本文算法框架被稱作inKD-Pr算法。

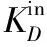
2 評估標準及數據集介紹

2.1 評估標準

本文采用SIR(Susceptible-Infective-Removal)模型[15],將節點的最大傳播力作為節點重要性評價標準。SIR模型是Kermack等提出的傳染病模型中最經典的模型,現在普遍應用于疾病傳播、謠言傳播等領域。

SIR模型將網絡節點分為三類:易感狀態S,指個體可能會被處于感染狀態的鄰居節點感染;感染狀態I,指節點已被感染且具備感染力;免疫狀態R,指節點失去感染其他節點的能力。剛開始傳播時,處在感染狀態I的節點,以β的概率感染處在S狀態的鄰居節點,隨后,處在I狀態的節點以概率γ轉變成為R狀態,不再參與傳染。重復上述步驟直至網絡到達穩態。模型可用微分方程表示如下:

在SIR模型中,全部節點的數量N=S(t)+I(t)+R(t),其中S(t)、I(t)、R(t)分別為在t時刻網絡中三種狀態節點的數量。

不同挖掘算法的優劣可通過各算法挖掘的重要節點在SIR模型上的傳播范圍來衡量。設置一個(組)重要節點為S狀態在SIR模型上進行傳播,觀察最終穩態時處于R狀態的節點數量。如果一種算法的挖掘結果可使網絡流傳播地又快又廣,即可說明該算法挖掘效果優于其他算法。

2.2 數據集

科布倫茨數據資料庫是公布在網上,供從事大規模數據處理的人員用來進行網絡科學及相關領域研究的工具。本文選取了該資料庫三個有向無權的網絡數據集作為實驗網絡,數據集信息如表2所示。

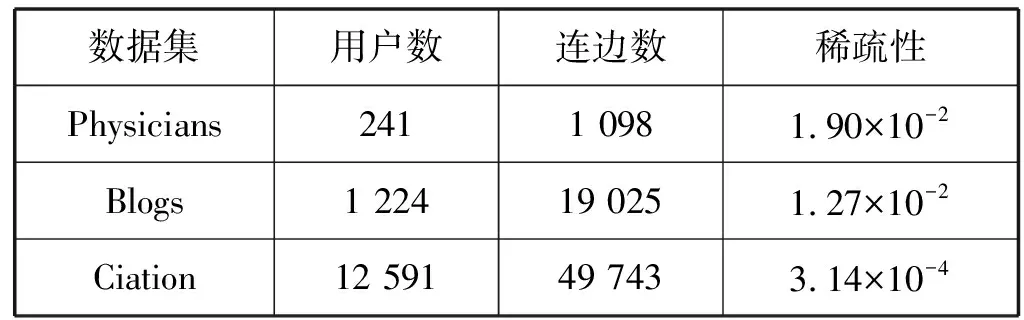
表2 數據集的基本特性

(1) Physicians社交網絡數據集:節點代表醫生,邊表示一位醫生遇到問題會向另一位醫生求助。

(2) Blogs超鏈接數據集:節點代表用戶,邊表示一個用戶鏈接了另一個用戶。

(3) Ciation數據集:節點表示一個機場,邊表示從一個機場到另一個機場的航班。

這三個數據集的基本情況如表2所示,稀疏性表示網絡中任意兩個節點間存在連邊的概率,即網絡中存在的連邊數量占網絡中所有可能連邊數的比例。在有向無環網絡中,網絡的稀疏性=m/[n(n-1)],其中:m為網絡中邊的數目;n為網絡中節點數。

3 仿真驗證

3.1 實驗設計

為了驗證本文方法的有效性,選取3種排序方法對比分析,分別是度中心性、PageRank算法、LeaderRank算法。

本文采用單一節點傳播的方式,分別對排名前k(為了分析方便,設置k=10)的節點進行SIR模型檢測,每個節點都作為單一感染源進行傳播,運行300次取均值,每種算法的有效性由該算法挖掘出的排名前10的節點傳播能力總和來表示。這里將免疫率γ取為0.5。對于感染概率β,如該值太小,很難在一個較小的網絡區域中區分開不同算法[16]。當β非常高,不管是從哪個節點開始傳播,最后傳播范圍都將覆蓋幾乎整個網絡,導致無法區分節點的作用。對此,本文使用一個溫和的感染概率β=0.3。

3.2 實驗結果

如圖4所示,將免疫狀態的節點的累計數量繪制成時間的函數,累計免疫節點隨時間增加,最終達到穩定狀態。在網絡規模較小時(如Physicians數據集),度中心性的表現要優于inKD-Pr算法和PageRank算法,但是度中心性算法的準確率與網絡規模有關,當網絡中節點數增多時,準確率呈現顯著下降趨勢。這種現象與度中心性本身的算法有關,度中心性僅以節點的局部信息作為衡量標準,而沒有考慮節點所處位置、更高階鄰居等因素,這就導致一些邊緣節點可以通過與大量普通節點建立連邊來提高度值,而這樣的算法,在inKD-Pr算法中完全占不到優勢,inKD-Pr算法以節點入度為參考值去提取核心網絡,既刪除了大量非核心節點,同時也確保了一些節點無法通過僅僅依靠增加出度而進入到核心網絡中。Blogs網絡上,度中心性算法和PageRank算法、inKD-Pr算法曲線近乎一致,即由這三種算法挖掘的前10名重要節點在網絡中的傳播能力基本相同。

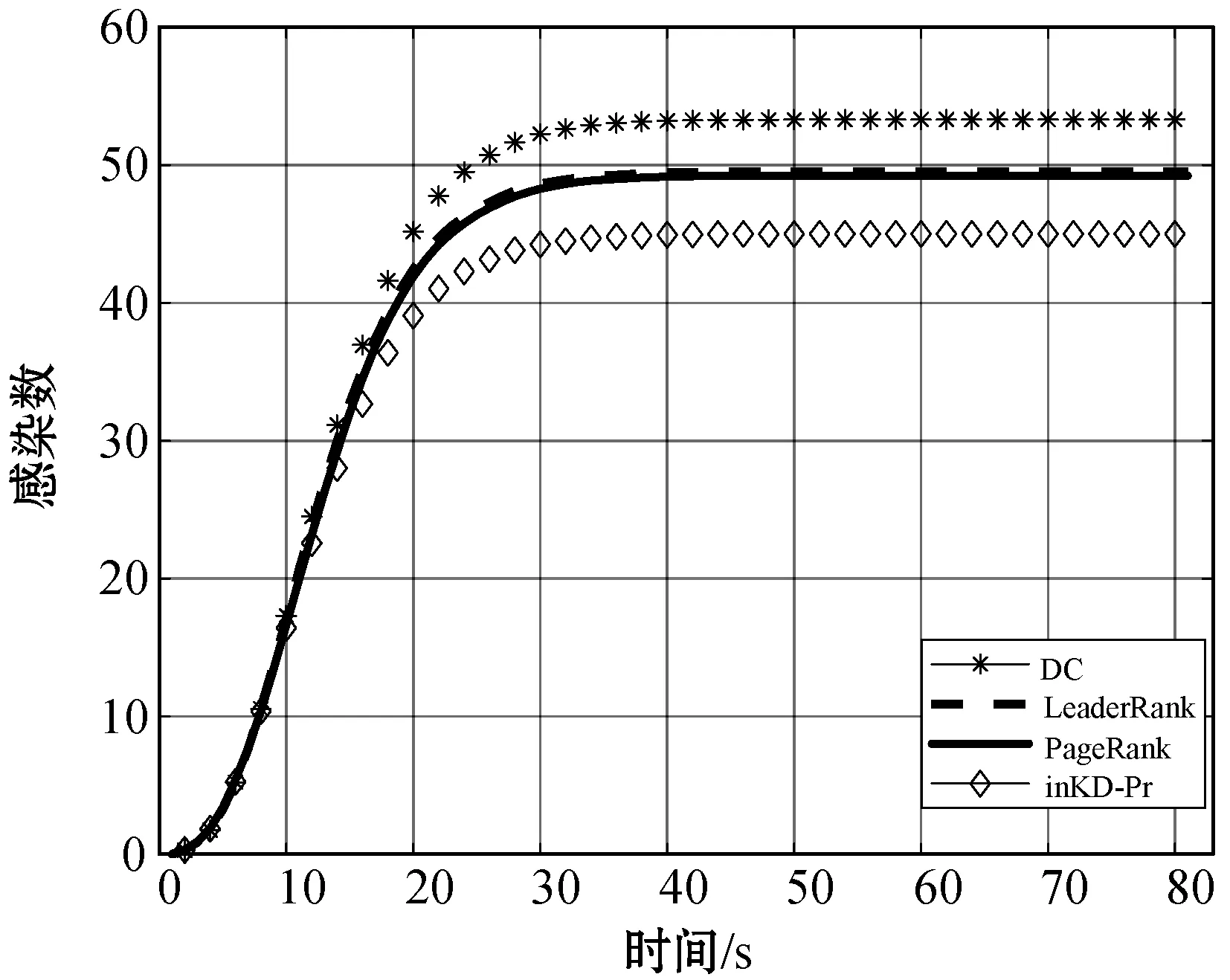
(a) Physicians網絡

LeaderRank算法和PageRank算法在準確度方面的穩定性較佳但算法復雜度高。LeaderRank算法的準確率始終優于PageRank算法,這是因為需要大量實驗才能獲取PageRank算法中的阻尼系數s,且會改變原來的矩陣結構。而LeaderRank[17]在PageRank的基礎上,加入一個與其他節點都有雙向連邊的節點,實現網絡的強連通,以此得到一個無參數的算法。實驗證明,這種算法比PageRank算法更準確。

inKD-Pr算法在網絡規模小的時候準確率比較低,這是因為K-Shell算法對網絡中的節點只能做粗粒度的劃分。節點的K-Shell值越大,節點就越重要[5]。但具體到兩個節點,只有K-Shell值相差很大,比如在10倍以上時,節點影響力才有顯著差距。而在小規模網絡中,節點的K-Shell值相差都不大,這就導致部分重要節點在用K-Shell分解法提取核心網絡時被刪除。在本文的實驗中可以看到,隨著網絡規模變大,這種算法的準確度也越高。在Ciation網絡中,inKD-Pr算法的準確率甚至優于LeaderRank算法,這是因為K-Shell分解法可以有效剔除一些大度節點的干擾。

3.3 準確率分析

本文將各算法挖掘出的Top-10節點與SIR模型挖掘出的Top-10節點進行對比,比值為各算法挖掘Top-10節點的準確率。表3的結果表明,網絡規模越大,度中心性挖掘算法的準確性越低。相比,在不同規模的網絡中,PageRank算法和LeaderRank算法具有更好的穩定性。本文提出的inKD-Pr算法隨著網絡規模增大,準確率也越高。但由于SIR模型每一次傳播到達穩態需要的時間比較長,本文最大只選取節點數為12 000多的社交網絡進行計算。從實驗結果可以預見,網絡規模越大,inKD-Pr算法挖掘重要節點的效果會更好。

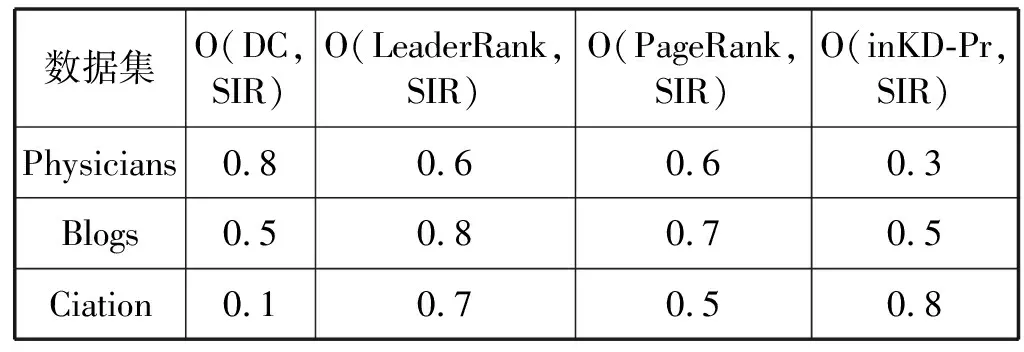
表3 各算法挖掘出的Top-10節點準確率與SIR模型對比

3.4 時間復雜度分析

本文提出的inKD-Pr算法是在K-Shell分解法的基礎上進行改進的,可近似看作O(n),與K-Shell分解法相同。PageRank的計算復雜度為O(mI),度中心性的時間復雜度為O(n),介數中心性的時間復雜度為O(mn),其中:n和m分別為網絡中的節點和邊的數量;I為迭代次數。從表4可以看出,本文所提出的inKD-Pr算法計算復雜度相對較低。

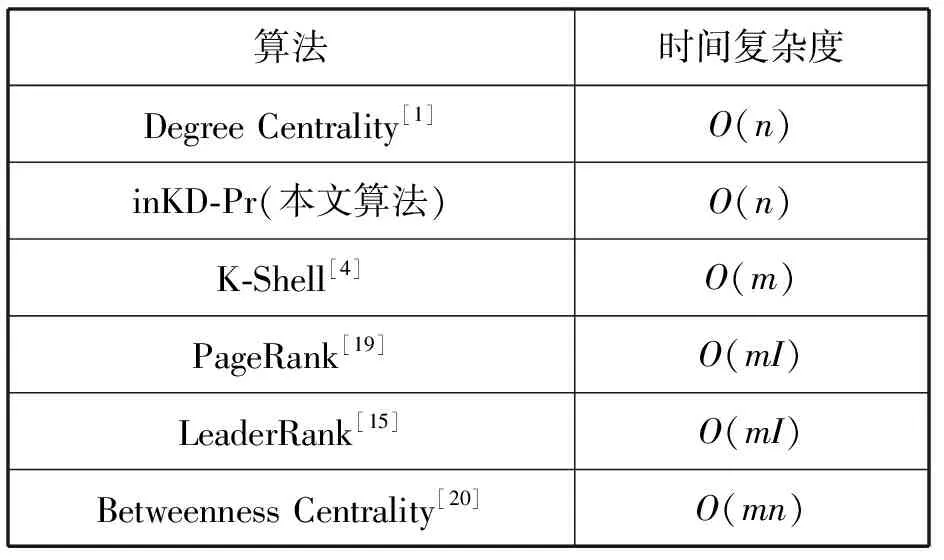
表4 部分重要節點挖掘算法時間復雜度

4 結 語