大范圍網格曲面曲線設計方法及應用

姜曉通,戴 寧,武智磊,楊思遠

(1.常熟理工學院 機械工程學院,江蘇 蘇州 215500;2.南京航空航天大學 機電學院,江蘇 南京 210016)

0 引 言

曲線設計是幾何造型中的一項重要研究內容[1-3],其在自由曲面的設計、交互和編輯中起著重要作用,且經常用于一些高級的幾何操作中,例如曲面求交[4]、曲面裁剪[5]、加工曲面的數控刀具軌跡規(guī)劃[6]等。針對歐氏空間的曲線設計的研究較早,相關的設計理論和算法已趨于成熟。但對于曲面上的曲線設計,因其在設計過程中需要滿足流行約束(曲線位于曲面上),其問題較為復雜,難度較大。近年來,隨著離散網格建模需求的快速增長,如在齒科領域的建模設計需求越來越多,離散網格曲面上的曲線設計逐漸受到人們的關注,因此研究網格曲面上曲線的設計方法具有重要意義和工程應用價值。

網格曲面上的曲線通常由離散的分段線段構成,常見的曲線形式有樣條曲線、測地線、細分曲線等。受流行的約束,其求解難度相對較大。為了處理流行約束問題,現有的網格曲面的曲線設計方法大致可以分為3類:投影法、光順法及參數化法。

投影法先在歐氏空間完成曲線設計,然后依次迭代將曲線投影到網格曲面上。Hofer等[7-8]提出能量最小化的樣條曲線插值方法,將問題表示為具有流行約束的優(yōu)化問題,基于樣條能量和測地能量對樣條曲線進行優(yōu)化,并采用梯度投影法進行求解,該方法可用于網格曲面、參數曲面、隱式曲面,但其投影步驟不能保證一定能計算出理想的投影點,魯棒性較差。Morera等[9]提出一種內蘊投影法來計算流行三角網格上的細分曲線,魯棒性得到了一定的改善,但由于設計測地線計算,時間復雜度較高。金耀等[10]用切平面逼近局部曲面,并將距離約束松弛成用點到切平面的距離,使曲線能夠逐步光順的同時,穩(wěn)步地貼近曲面,從而使投影步驟的魯棒性和可靠性大為提高。投影法實現方式簡單,但是由于需要迭代,使得計算量較大,且對于復雜曲面投影可能存在多解,魯棒性較差。

光順法首先對光滑約束進行松弛,然后在流行約束下以光滑能量為驅動對初始曲線進行光順。Jung等[11]在網格曲面上運用主動輪廓模型演化曲線,在曲面上對曲線進行分段光順,使曲線演化到具有高斯曲率相關特征附近。Lawonn等[12]提出一種網格曲線的拉普拉斯光順算子,通過降低測地曲率來對三角網格上分段曲線進行光順,可以調整光順曲線與其原始形狀的接近程度以及規(guī)定測地線曲率的偏差,但需要對曲線進行多次迭代且無法插值控制點。宋瀅等[13]提出了一種基于多層次優(yōu)化的網格域樣條曲線設計方法,該方法放松了曲線嚴格位于曲面的約束,僅將曲線的離散控制點置于流形空間,并采用內點法的思想,運用基于塊坐標下降法的全局優(yōu)化方法進行數值求解,最后借助局部參數化將曲線段映射到網格曲面。光順法魯棒性較好,曲線也較為光順,但由于需要進行多次迭代且無法插值控制點,因此計算效率低,難以滿足曲線實時交互的要求。

參數化法將曲線所在的設計區(qū)域進行參數化,在參數域內進行曲線設計,并將曲線設計結果映射回網格曲面。Lee等[14]提出了一種“幾何蛇形”曲線作為三角網格模型的特征檢測工具,將曲線所在的局部區(qū)域進行參數化,在參數域內使用能量函數演化曲線從初始位置成功捕獲附近的特征;朱文明等[15]通過對流行網格進行保角參數化,并在參數域內生成細分曲線,可以快速生成網格曲面上的光滑曲線;韓林等[16]使用離散指數映射技術參數化B樣條曲線的控制頂點,實現了網格曲面上B樣條曲線的設計與復用。劉斌等[17]通過離散指數映射參數化技術將源曲線控制頂點映射到切空間,獲得它們的法坐標,按照陣列前后控制頂點法坐標不變的原則,實現了曲線在網格曲面上的陣列。參數化法對于小范圍曲線設計魯棒性較好,計算效率高,曲線設計較為靈活。但當進行大范圍的曲線設計時,大范圍的曲面參數化較為耗時,影響了曲線設計的效率,難以實現曲線的實時編輯,同時大范圍的曲面參數化會導致局部參數化畸變嚴重,甚至出現大面積的“重疊”現象,導致曲線在局部畸變的情況,甚至會引起在曲線設計時求交算法的不穩(wěn)定性問題。另外,參數化方法并不能完全適用于網格曲面存在“虧格”的情況,也限制了參數化方法的適用范圍。

齒科是離散網格曲面應用最為廣泛的領域之一,齒科掃描模型的復雜性及相關建模軟件個性化設計的需求,其對樣條曲線的設計也提出了具體要求,主要有如下特點:

(1)齒科三維掃描模型三角面片個數較多,在曲線設計時需要進行實時編輯,要求曲線設計效率較高,能夠滿足實時交互的需求;

(2)齒科三維掃描模型較為復雜,對曲線設計的精度要求不高,但建模軟件的使用人員在繪制曲線時較為“隨意”,因此對魯棒性提出了較高的要求;

(3)因建模軟件的設計要求,需要基于網格曲線進行個性化建模,因此對樣條線的設計原理提出了具體的要求。

該文針對在齒科建模領域中,對于網格曲線設計在高效性、魯棒性及基于網格曲線個性化建模等方面的要求,提出了一種適用于大范圍網格曲面曲線編輯的參數化設計方法,使用離散指數映射參數化技術,將三維的曲線設計轉換成二維曲線設計,在二維平面內進行基于曲線的建模設計,滿足建模軟件個性化建模的需求。利用分段樣條線替代全局樣條線,分段設計網格曲面樣條曲線,減小參數化區(qū)域,能夠實現在大范圍網格曲面內快速設計曲線,同時將參數化設計方法擴展到虧格網格曲面。針對建模軟件使用人員在建模過程中繪制曲線較為“隨意”,樣條曲線兩型值點間距較大而導致的魯棒性問題,引入兩點間的最近路徑,在兩型值點中加入若干型值點,滿足離散建模軟件對算法魯棒性的要求。針對曲線分段設計時在部分型值點處出現不連續(xù)(尖點)的問題,在型值點處進行局部光順,從而保證曲線的質量。相比其他方法,該算法在效率、魯棒性及適用性等方面具有一定優(yōu)勢,綜合性能較好。

1 離散指數參數化技術

1.1 指數映射及測地極坐標

設Tp是曲面S在p點的切平面,那么指數映射就是從切平面Tp到曲面S上的一個對應關系,記為Tp→S,定義如下:設v是曲面S在p點的一個切向量,過點p作曲面S上與切向量v相切的測地線γ,在此測地線上取一點m,使得從p到m的弧長正好等于v的長度|v|,則定義指數映射exp(v)=m。

指數映射可以看作是曲面到切平面的一種映射,它將曲面上的三維空間上的點映射到二維平面上(見圖1)。對于曲面S上任意一點p,過點p作其切平面Tp,對任一單位向量v∈Tp來說,都唯一存在一條用弧長來參數化的測地線γ,使得γ(0)=p且γ(0)'=v。對于p點的任一鄰域點q來說,都會有唯一的一條測地線通過它。因此,可以使用測地極坐標(ρ,φ)將三維空間點q映射到二維切平面Tp上,其中ρ是p點到q點的測地線距離,φ是v在Tp上的極角,這就是測地極坐標的表示形式,也可以將其看作二維矢量,稱作測地矢量。

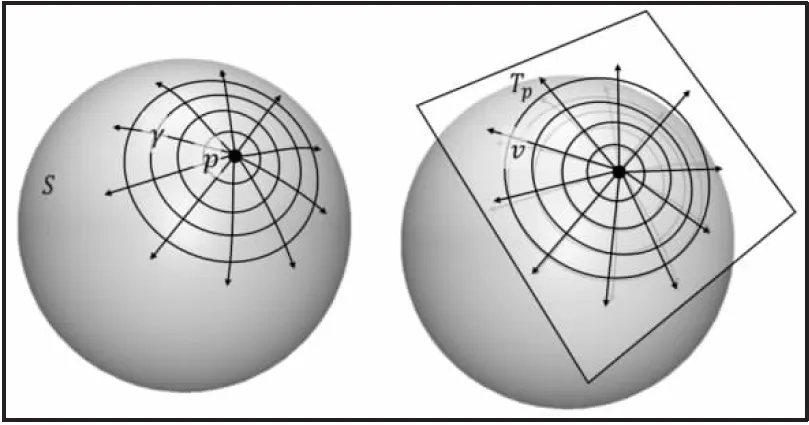
圖1 指數映射

1.2 離散指數映射參數化基本原理

該文采用Schmidt等[18]提出的離散指數參數化技術計算測地矢量,該方法并不直接計算網格曲面上的點到種子點的測地矢量,而是通過Dijkstra算法進行擴散傳播,先記錄每個網格頂點到種子點的路徑并在每個網格頂點上建立局部坐標系,然后對每個網格頂點向其最短路徑上的前一個鄰接頂點作指數映射,最后對Dijkstra算法產生的分段測地矢量進行疊加。

如圖2所示,假設網格曲面上有3個頂點,分別為p、r、q,可以根據指數映射理論計算出p點到r點的測地矢量Up,r和r點到q點的測地矢量Ur,q,則p點到q點的測地矢量Up,r可以表示為:

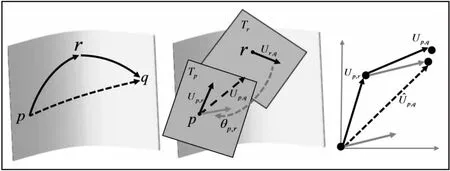
圖2 離散指數映射疊加

Up,q=Up,r+(Up,q-Up,r)

(1)

Up,q≈Up,r+Rot2D(θp,r)Ur,q

(2)

式中,Rot2D為二維旋轉變換矩陣。

對于網格模型上的任意一個頂點q,利用Dijkstra算法生成從種子點p到目標點q的近似測地路徑,利用公式(2)計算得到該路徑中每一個頂點在種子點p所在切平面上的坐標值。由于公式(2)在變換過程中存在誤差,該誤差在從點p到點q的近似測地路徑會累計疊加,因此在進行大范圍網格曲面的參數化或網格曲面較為復雜時,其參數化結果會產生較大畸變,甚至“重疊”現象。但是若不謀求網格全局參數化,只考慮局部映射,其精度是能夠保證的。同時由于離散指數映射無需計算測地線,減小了計算成本,非常適用于三角網格的局部快速參數化,對于分段樣條曲線的設計具有很大優(yōu)勢,能夠滿足曲線編輯實時交互的要求。

2 分段樣條曲線設計

2.1 準均勻B樣條曲線

給定條件①控制頂點:P0,P1,…,Pn;②B樣條曲線基函數的次數k;③節(jié)點矢量:[u0,u1,…,un,…,un+k+1],可以唯一定義k次B樣條曲線為:

(3)

式中,u∈[uk,un+1]。

根據均勻B樣條基函數的遞推定義,可以得到均勻3次B樣條曲線基函數如下:

(4)

準均勻B樣條曲線就是在均勻B樣條曲線的基礎上增加了k+1個重節(jié)點的限制,使其不僅具有均勻B樣條的局部支撐性,即當用戶想要改變型值點的位置,只需重新計算該型值點臨近的樣條曲線即可,而且準均勻B樣條具有Bezier曲線的端點性質,使用戶對曲線在端點處的行為有較好的控制。因此,文中算法采用準均勻B樣條曲線在參數化平面內生成樣條線。

2.2 局部分段樣條曲線

給定一個離散網格曲面S,在網格曲面上依次拾取型值點p0,p1,…,pn,文中算法僅利用最新拾取的三個型值點,在局部參數域內生成分段的準均勻3次B樣條曲線,并對整體樣條曲線進行局部更新,算法主要分3步:

(1)確定參數化區(qū)域。

離散指數映射是一種局部參數化技術,在計算參數化區(qū)域時,需要給定參數化原點和半徑,參數化區(qū)域必須盡可能覆蓋測地B樣條曲線設計區(qū)域。假設在繪制當前樣條曲線時正拾取第i個型值點。

當i=0時,型值點個數為1,無需繪制網格樣條曲線。

當i=1時,2個型值點為p0,p1,此時參數化原點為任意一個型值點,將p0和p1之間的歐氏距離記作|p0p1|,則參數化半徑paraDis=1.4|p0p1|,此時生成的為一段測地直線。

當i=2時,3個型值點為p0,p1,p2,則參數化原點為p1,參數化半徑paraDis=1.4max{|p0p1|,|p1p2|},此時生成的為一段測地樣條曲線,此后用戶繼續(xù)增加型值點,則總是取最后三個型值點pi-2,pi-1,pi生成一段測地樣條曲線,其中參數化原點和半徑的確定方法與上述一致。

(2)二維參數化平面上的樣條曲線設計。

將三個型值點為一組的樣條曲線段所在網格區(qū)域進行參數化后,可以得到型值點的二維UV坐標。根據型值點的UV坐標及非均勻B樣條曲線插值方法可以生成位于參數化平面上的二維樣條曲線,但由于網格曲線通常由離散的分段線段構成,因此需要對樣條曲線段進行采樣。由于采樣點只有坐標信息,沒有網格位置信息,并且型值點和采樣點之間連線與網格的交點未知,因此需要進行計算。給定起點ps和終點pt,計算過程如下:

①若起點ps在網格三角面片面內,計算起點ps和終點pt連線與起點ps所在三角面片相交的邊,并將計算得到的交點pc賦值給ps,更新起點。

②若起點ps在網格邊上,與起點ps所在網格邊共邊的有兩個三角形,判斷起點ps和終點pt連線經過哪個三角形,并確定連線與該三角形相交的邊,并將計算得到的交點pc賦值給ps,更新起點。

③重復上述過程直至到達終點pt。

(3)二維參數化平面到三維網格曲面的映射。

二維平面內的樣條曲線設計完成后,需要將其映射回三維網格曲面。假定在二維參數化網格平面取樣條曲線上任一點為p,點p所在三角面片的三個頂點V0,V1,V2可以定義平面內包圍該點的凸多邊形,用公式可以表示為:

(5)

構造方程組并求解可得到α0,α1,如圖3所示,(α0,α1,1-α0-α1)代表點p相對于三角面片三個頂點的相對位置關系。

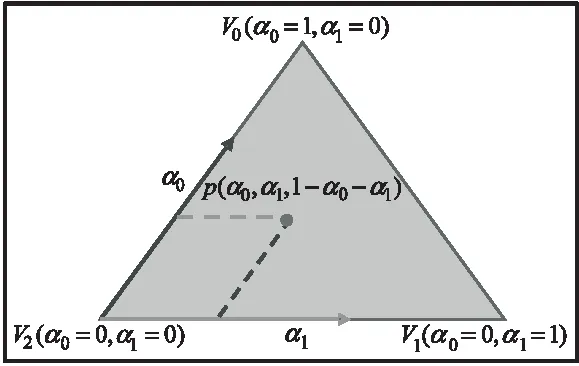
圖3 三角形內一點p相對位置關系

由于離散指數參數化技術并不改變三角面片的形狀,因此利用公式(5)可以將二維參數化平面上三角面片上的任意一點映射回其三維網格上的三角面片上,則點p的三維空間坐標p3可表示為:

(6)

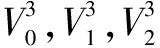
2.3 樣條曲線優(yōu)化

(1)最短路徑優(yōu)化。

在實際工程應用中,用戶在繪制網格樣條曲線時較為“隨意”。當相鄰兩型值點距離過大時會導致參數化區(qū)域增大,而離散指數參數化技術在參數化區(qū)域過大時會產生較大的網格畸變、重疊等現象,從而導致兩型值點之間的樣條線不光滑,甚至樣條線中斷的情況,如圖4(a)所示。為了提高算法的穩(wěn)定性,避免用戶在設計曲線時出現上述情況,引入Dijkstra算法計算兩點間的最短路徑,在兩型值點之間的最短路徑上進行采樣,在采樣路徑上增加型值點的個數,從而有效避免上述情況的出現,如圖4(b)所示。

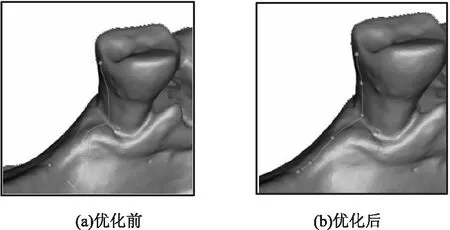
圖4 最短路徑優(yōu)化

(2)局部光順優(yōu)化。

在網格曲面生成樣條曲線時,因為采用分段樣條線策略,因此在型值點處會出現“尖點”,從而降低了曲線的光順性,如圖5(a)所示。針對此問題,文中算法在型值點處進行局部光順。設給定離散網格曲線點列Pi(i=0,1,…,n),該離散點列的能量可表示為:

圖5 局部光順優(yōu)化示意圖

(7)

在對離散點列進行光順時有兩個原則:一是光順后離散點列的能量Ec盡可能小,二是光順后離散點列的偏離盡可能小。綜合以上兩點,給出如下所示的離散點列的加權綜合光順方法:

(8)

式中,Pi(i=0,1,…,n)為光順后的離散點列;Qi(i=0,1,…,n)為光順前的離散點列;Ec為離散點列Pi的能量;α和β為用戶指定的非負常數。如圖5(b)所示,采用上述方法對型值點附近的離散點列進行光順后,曲線的光順性得到了明顯提高。

3 實驗結果與分析

文中算法利用C++語言,在Visual Studio2017環(huán)境下開發(fā),模型顯示是基于VTK圖形庫,在AMD Ryzen 7 5800H處理器主頻為3.20 GHz,16 GB內存的電腦上測試。測試過程中所有的數據都來源于實際掃描數據,驗證算法的有效性與實用性。

3.1 算法的實際設計效果

圖6為文中算法在牙頜模型上的實際曲線設計效果。因采用分段樣條線策略,該算法能夠實現大范圍網格曲面樣條曲線的實時設計。同時在進行曲線編輯時,拖動一個型值點只改變該型值點附近的一段曲線而不會改變整段曲線的形狀,能夠快速對曲線進行編輯修改。

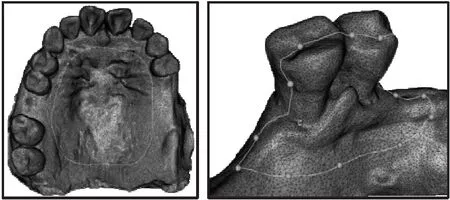
圖6 牙頜模型上的曲線設計

該算法因采用局部參數化進行分段曲線設計,能夠在虧格模型上進行曲線設計。圖7展示了利用該算法在虧格模型上進行的曲線設計,該曲線可以環(huán)繞虧格,而基于全局參數化的曲線設計方法則無法在虧格模型上生成如圖所示的曲線。

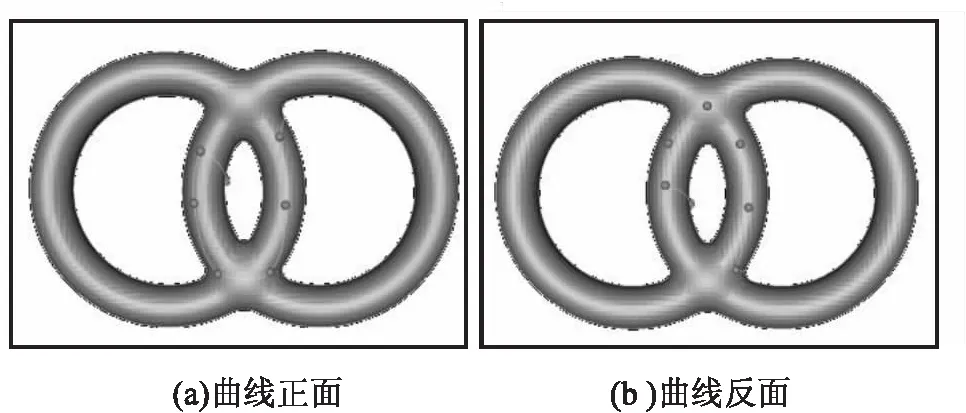
圖7 虧格模型上的曲線設計

3.2 樣條曲線設計效率

在齒科建模工程應用中,曲線設計需滿足實時交互的要求,即曲線設計算法必須高效。為了驗證文中算法的高效性,選擇如圖8所示的4個不同規(guī)模的模型進行測試。

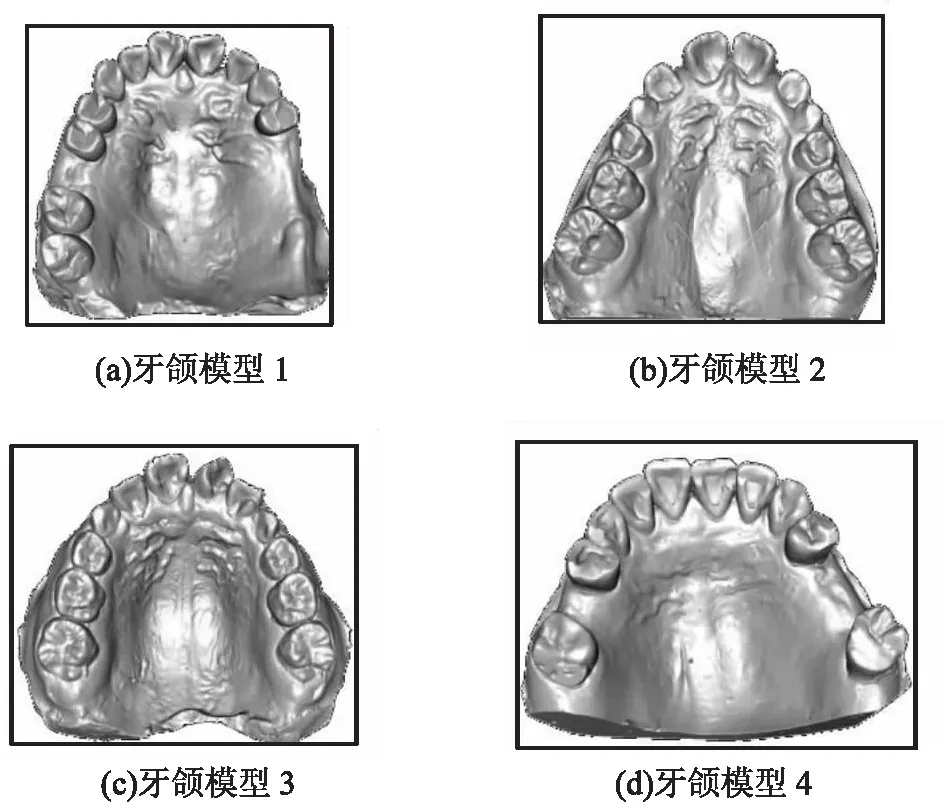
圖8 不同牙頜模型上的曲線設計

在測試過程中,分別在不同模型上選取3個型值點生成樣條曲線,并計算生成這段曲線所需時間。表1為在這些模型上生成曲線所用的時間。

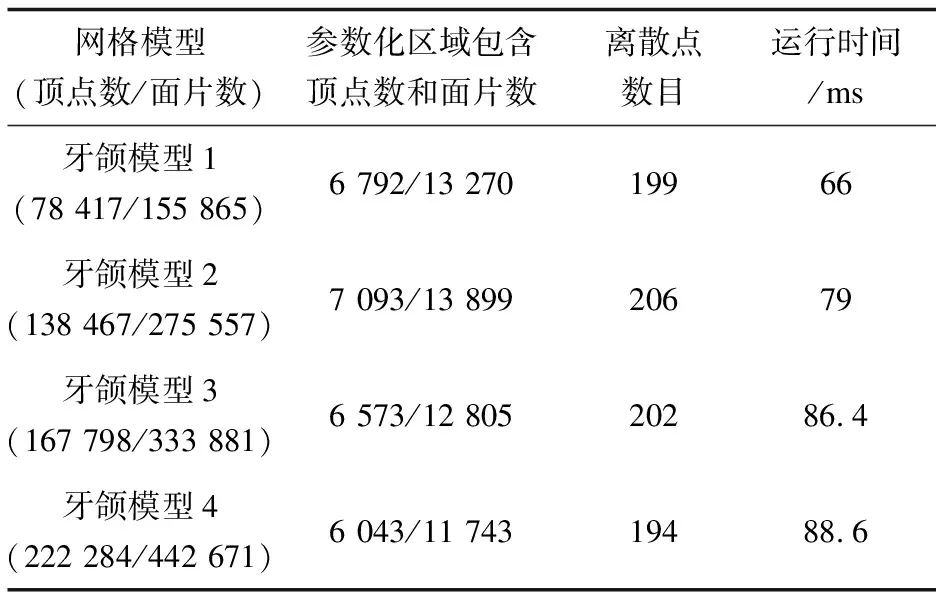
表1 不同的模型上網格曲線的生成時間

從表中可以看出,當樣條曲線離散點數大致相同時,參數化區(qū)域大小(頂點數和面片數)相差不大。但隨著模型頂點數和面片數的增加,運行時間會相應增加。但從表中可以看出網格規(guī)模與算法效率的相關度較小,在網格頂點數為22萬,曲線離散點數為194時,其計算時間僅為88.6 ms,可以滿足實際工程應用中曲線設計實時交互的要求。

圖9為網格頂點不同量級的牙頜模型在模型表面的同一位置上繪制的網格曲線,計算曲線在每一個模型的生成時間,其結果如表2所示。

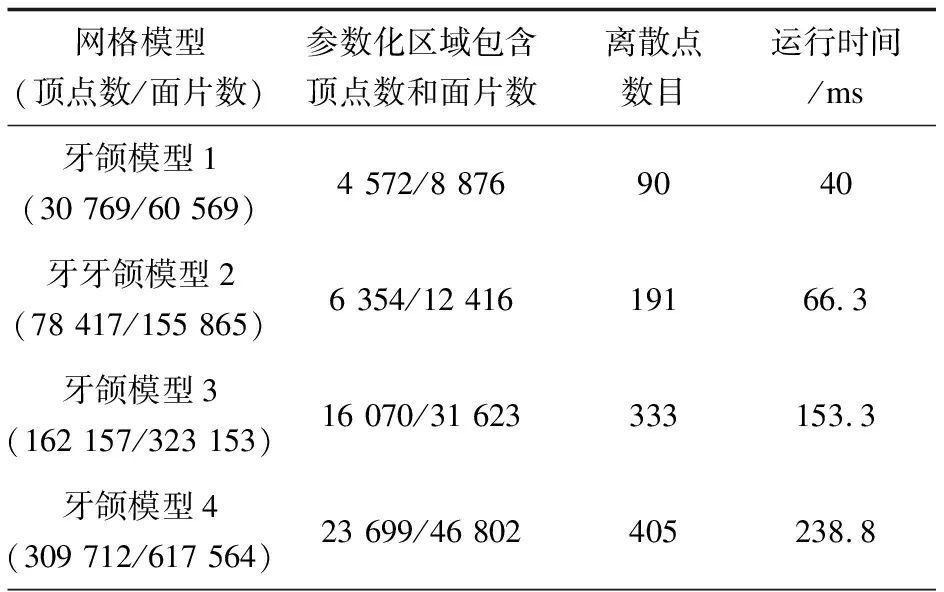
表2 不同規(guī)模的同一模型上網格曲線的生成時間

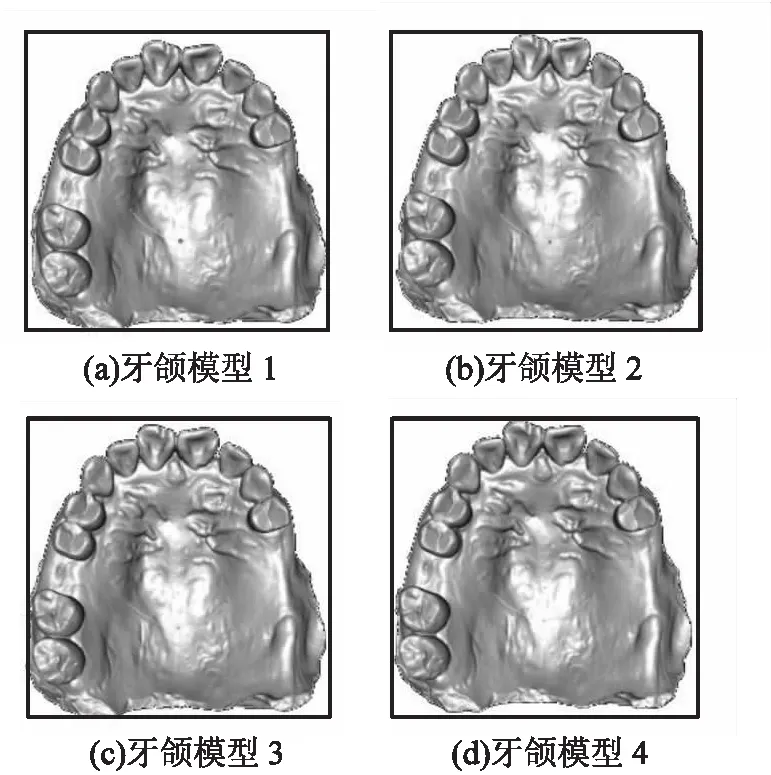
圖9 不同規(guī)模的牙頜模型上同一位置的曲線設計

從表中可以看出,隨著模型頂點量級的增大,參數化區(qū)域大小(頂點數和面片數)會相應增大,導致所生成的曲線包含的離散點數增多,生成曲線的時間也隨之增加,與參數化區(qū)域頂點的個數基本上成正比。

從上述兩個測試實驗可以看出,文中算法的效率主要受局部參數化區(qū)域內網格頂點的數量的影響,局部參數化網格頂點越多,效率越低,而網格模型總頂點數量對算法效率的影響較小,因此文中算法能夠在大規(guī)模網格模型上進行高效的大范圍曲線設計,能夠滿足工程應用的要求。

3.3 實驗對比

文中算法是為滿足網格曲線在齒科建模軟件中的應用而設計,為了驗證算法的效果,從曲線的光滑度、效率、局部編輯性及擴展應用性等方面與文獻[10,13]進行比較與分析,如表3所示。

表3 算法比較

文獻[10,13]的算法都屬于投影法和光順法相結合的算法。在曲線光順度方面,由于該文采用分段樣條曲線進行設計,并對樣條線進行局部光順,因此相比文獻[10,13]的算法,文中算法生成的曲線光順度相對較差,但由于文中算法主要應用于齒科建模軟件中,其對曲線的光順度要求不高,能滿足要求。在效率方面,文獻[10]的算法效率最高,在模型點數3 070,曲線離散點數258的情況下,其運行時間為12.5 ms;文獻[13]的算法和文中算法次之。文獻[13]的算法,在模型點數15 000,曲線離散點數190的情況下,其運行時間為39 ms,而文中算法在模型點數78 417,曲線離散點數199的情況下,其運行時間為63 ms。在局部編輯性方面,由于文獻[10,13]的算法對曲線進行全局光順,因此在改變曲線的一個型值點時,整個曲線都會發(fā)生相應的變化;而文中算法采用分段樣條曲線,因此在進行曲線編輯時,改變曲線一個型值點,其作用范圍只局限于該型值點前后兩個型值點之間的曲線,因此文中算法的局部編輯性更好。在應用擴展性方面,文獻[13]的算法松弛了曲線嚴格位于曲面的約束,因此并不能用于曲線裁剪、基于曲線的個性化建模(圖10所示)等方面;文獻[10]的算法中的曲線嚴格約束于網格曲面上,因此可以應用于曲線裁剪,但在齒科建模軟件中基于曲線的個性化建模中,該算法生成的曲線并不適用;而文中算法因采用局部參數化方法,可以在垂直于樣條線走向的方向上生成一系列具有一定寬度的直線,通過鋪面、抽殼等操作生成具有一定形態(tài)的三維模型(如圖10(b)所示的卡環(huán)),同時算法嚴格約束于曲面,因此可以用于曲線裁剪。

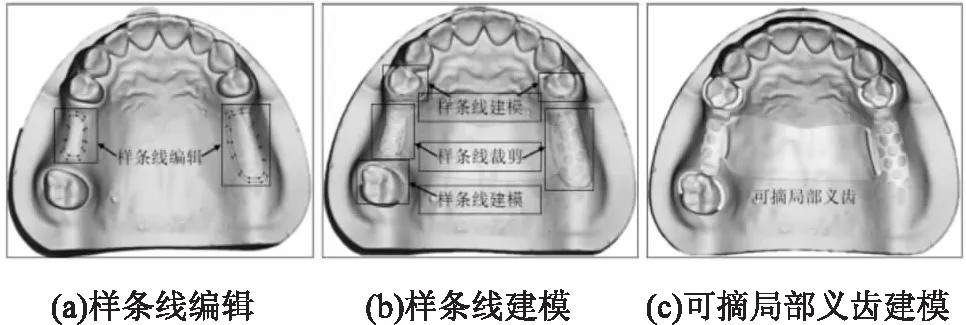
圖10 可摘局部義齒建模

3.4 基于樣條線的建模應用

圖10為文中算法在齒科建模軟件中的應用。圖10(a)為利用文中算法在牙頜模型的不同區(qū)域進行網格裁剪,生成子網格,用于網格模型局部區(qū)域的偏置。圖10(b)為利用文中算法在牙頜模型上進行基于樣條曲線的三維建模,在牙頜模型上生成卡環(huán)、連接體等(沿著樣條曲線方向,具有一定寬度且與原始模型緊密相貼的條狀或半圓柱狀模型),用于可摘局部義齒的設計。圖10(c)為利用文中算法完成的可摘局部義齒的設計。

4 結束語

該文提出了一種基于局部參數化的離散網格曲面樣條曲線設計方法。該方法放松了對樣條曲線全局連續(xù)性的約束,將平面參數域內的全局樣條線設計轉化成在局部區(qū)域內的分段樣條曲線設計。同時引入兩型值點間的最短路徑,解決在樣條線設計過程中,因相鄰兩型值點距離過大而導致算法存在的魯棒性問題,引入局部光順算法,提高網格曲線在型值點附近的光順性。相比于全局參數化的網格曲線設計方法,該方法魯棒、高效,并且能滿足大范圍網格實時編輯的要求,綜合性能較好。

該方法采用局部參數化方法進行曲線設計,其中參數化區(qū)域大小(頂點數和面片數)對曲線設計效率影響較大,而算法所生成的參數化區(qū)域為距離中心點參數化半徑范圍內的所有三角面片,一定程度上造成了計算的浪費,因此如何識別曲線所在網格區(qū)域,從而減小參數化區(qū)域是未來需要研究的工作。