雙變量與條件地震重現期理論及應用

王曉磊，呂大剛，閻衛東

(1.沈陽建筑大學土木工程學院，遼寧，沈陽 110168；2.河北省地震災害防御與風險評價重點實驗室，河北，三河 065201；3.哈爾濱工業大學土木工程學院，黑龍江，哈爾濱 150090)

重現期是具有概率含義的重要概念：對于離散型隨機變量，重現期是服從幾何分布的首次等待次數平均值；對于連續型隨機變量，重現期是服從指數分布的首次等待時間平均值。

重現期概念在一些工程領域已得到了廣泛應用[1?17]。在地震工程領域，重現期是超越某地震動強度參數大小的平均發生時間，也被稱為平均地震重現期(簡稱地震重現期)，已廣泛應用于工程結構抗震設計與評估中：呂大剛等[1]總結比較了中國《建筑抗震設計規范》[2]、中國地震動參 數 區 劃 圖[3]、美 國NEHRP[4]、FEMA 273[5]和SEAOC Vision 2000[6]規定的小震、中震、大震和巨震對應的地震重現期；李慧[7]總結比較了中國、美國、歐洲和日本抗震規范規定的設防目標對應的地震重現期；楊成等[8]基于地震重現期進行了橋梁行車安全易損性分析；王曉磊[9]基于場地危險性生成了我國某核電廠址地震重現期，并進行了核電廠安全殼概率地震風險評估。

目前，地震工程領域的重現期通常指的是單個地震動強度參數超越指定強度大小的重現時間，即基于標量型概率地震危險性分析獲得的單變量地震重現期，無法考慮地震動強度參數間相關性[9?10]。基于上述研究現狀，為了選取具有多個強度參數一致危險性的地震動記錄，DU[10]提出了三類多變量地震重現期概念，包括：同時超越多變量重現期、任一超越多變量重現期和Kendall函數多變量重現期，并詳細研究了基于三類多變量重現期的地震動記錄選取理論方法與現有地震動選取方法的優劣，發現基于Kendall 函數多變量重現期選取的地震動記錄更具有一致危險性[11?12]。DU 僅將多變量重現期在地震動選取方面進行了應用研究，對基于向量型概率地震危險性分析的多變量重現期研究還不深入，同時也沒有涉及條件地震重現期理論與應用方面的研究。在水文工程領域，重現期理論得到了更為深入的發展和應用[13?14]，包括：單變量重現期、多變量重現期和條件重現期等。相較于水文工程，地震工程具有自身理論與應用特點，地震重現期在水文領域多變量和條件重現期基礎上，還需要考慮地震工程理論與應用特點。目前，地震工程領域中向量型概率地震危險性分析理論[18]和條件型概率地震危險性分析理論[19]得到了不斷應用和發展，基于上述研究現狀，需要對基于向量型概率地震危險性分析與條件型概率地震危險性分析為基礎的多變量地震重現期和條件地震重現期理論與應用進行深入研究。

基于目前地震工程領域中重現期的研究現狀，本文提出了考慮地震動強度參數間相關性的雙變量地震重現期與條件地震重現期概念，給出了雙變量地震重現期與條件地震重現期的理論基礎，基于某個算例場地地震危險性信息，計算了雙變量地震重現期與條件地震重現期分布，并對雙變量地震重現期與條件地震重現期進行了應用研究，最后給出了考慮地震動強度參數相關性的雙變量地震重現期與條件地震重現期理論與應用研究展望。

1 地震重現期基本理論

本節首先總結了地震工程領域單變量地震重現期基本理論，然后提出了包含兩個強度參數聯合發生信息的雙變量地震重現期和條件地震重現期概念，并總結了雙變量地震重現期與條件地震重現期基本理論。

1.1 單變量地震重現期基本理論

1.1.1 單變量重現期基本理論

單個隨機變量的累積分布函數可以表示為：

式中：Pr[]為事件發生概率函數；X為隨機變量；x為目標值。

單個隨機變量的余累積分布函數可以表示為：

那么，單變量重現期可以表示為單個隨機變量的余累積分布函數的倒數：

1.1.2 單變量地震重現期基本理論

地震工程領域中地震重現期是針對單個地震動強度參數的重現時間，是單變量地震重現期。參照單變量重現期基本概念，可以構造單變量地震重現期理論公式。首先，進行標量型概率地震危險性分析，基于標量型概率地震危險性分析理論，單個地震動強度參數在指定強度大小下的年平均發生率可表示為：

式中：νi為地震年平均發生率；P{S a(Tj)>sj|m,r,θ}是震級、距離和方向角等參數條件下強度參數S a(Tj)超越sj強度水準的發生概率；fM,R,θ(m,r,θ)為震級、距離和方向角等參數的概率密度函數；sj為指定強度大小。

地震發生通常假設服從指數分布，那么地震動強度參數t年內超越概率可表示為：

式中：λ (sj) 為地震動強度參數超越sj的年平均發生率；N為超越次數；t為統計基準期。

參照上述單變量重現期基本理論，可表示單變量地震重現期理論公式為：

式中，P為地震動強度參數在統計基準期t年內超越概率。

將對數函數 ln(1?P)1t進行泰勒級數展開[20]，取泰勒級數第一項，單變量地震重現期理論公式可簡化為[21]：

1.2 雙變量地震重現期基本理論

1.2.1 雙變量重現期基本理論

假設兩個隨機變量X和Y的累積分布函數可分別表示為：

式中：Pr[]為事件發生概率函數；X和Y為兩個隨機變量；x和y為目標值。

同時，隨機變量X和Y聯合發生的累積分布函數可以表示為：

隨機變量X和Y同時超越的累積分布函數可以表示為：

隨機變量X和Y同時超越的平均發生重現時間可以表示為：

1.2.2 雙變量地震重現期基本理論

在單變量地震重現期理論基礎上，進一步考慮地震動強度參數間相關性，可表示為多變量地震重現期，由于多個地震動強度參數的向量型概率地震危險性分析計算量比較大并且應用還不夠廣泛，本文僅介紹基于兩個參數的雙變量地震重現期概念和理論。基于雙變量重現期理論公式，可構建雙變量地震重現期理論，兩個地震動強度參數聯合發生的超越概率可基于向量型概率地震危險性分析得到，兩個變量的向量型概率地震危險性分析可表示為：

式中：νi為地震年平均發生率；fS a1,S a2(x1,x2|m,r,θ)為震級、距離和方向角等參數條件下兩個強度參數同時超越某強度大小的聯合發生概率密度函數；fM,R,Θ(m,r,θ)為震級、距離和方向角等參數的概率密度函數。

兩個強度參數同時超越的年平均發生率可表示為：

根據地震工程領域中地震動強度參數聯合超越理論，基于式(12)，可以構造地震工程領域雙變量地震重現期的計算公式：

雙變量地震重現期與單變量地震重現期存在以下關系：

式中：TSR(x)和TSR(y) 為單變量地震重現期；TVR(x,y)為雙參數同時超越的地震重現時間，本文指定該重現期為地震工程領域的雙變量地震重現期。

由式(16)可發現，雙變量地震重現期通常大于等于兩個單變量地震重現期。同時，由上述理論陳述可發現：雙變量地震重現期在傳統單變量地震重現期基礎上，考慮了地震動強度參數間相關性。

1.3 條件地震重現期基本理論

1.3.1 條件重現期基本理論

本文僅針對單個條件參數并且預測參數為單個的條件重現期進行分析，該條件重現期可表示為：

式中：F(x|Y≥y) 是 以變量Y≥y為條件的X≤x發生的累積分布函數。

條件概率計算公式可表示為：

式中：Pr(X≥x,Y≥y)為變量X和Y聯合發生概率；Pr(Y≥y)為變量Y邊緣發生概率。

基于條件計算式(18)，可以得到單參數條件重現期另一表達式為：

式中：T′(x,y) 為雙參數同時超越的重現期；TY為單參數超越的重現期。

1.3.2 條件地震重現期基本理論

條件地震重現期可以基于兩種方式獲得：1)基于單變量地震重現期和雙變量地震重現期結果，利用條件發生概率理論公式生成；2)基于條件型概率地震危險性分析，計算強度參數條件超越概率，生成條件地震重現期。

地震動強度參數條件發生概率可由條件型概率地震危險性分析得到，條件型地震發生概率密度函數可表示為：

式中：fS a2|S a1(x2|x1,m,r,θ)為給定條件下的強度參數Sa2條件發生概率密度函數；fM,R,Θ(m,r,θ|,x1)為震級、距離和方向角的條件發生概率密度函數。強度參數條件型超越概率可表示為：

根據地震工程領域中地震動強度參數條件超越理論，基于式(17)，條件地震重現期可表示為強度參數條件型超越概率的倒數：

基于條件概率公式，條件地震重現期與雙變量地震重現期和單變量地震重現期關系可以表示為：

式中：TVR(x,y)為雙變量地震動強度參數同時超越重現期；TSR(y)為單變量地震動強度參數超越重現期。

由上述理論表述，可發現：條件地震重現期在傳統單變量地震重現期基礎上，進一步考慮了地震動強度參數間相關性。

2 單變量、雙變量和條件地震重現期生成步驟

2.1 單變量地震重現期生成步驟

單變量地震重現期可基于標量型概率地震危險性分析結果生成，生成步驟如下(流程圖如圖1所示)：

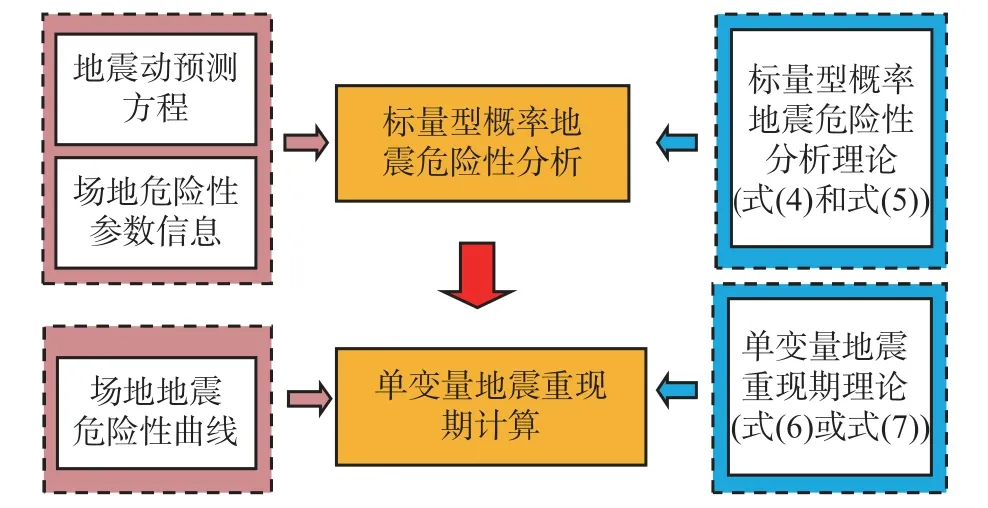
圖1 單變量地震重現期計算流程圖Fig.1 Flowchart of single variable earthquake return period calculation

1)基于場地危險性數據，采用標量型概率地震危險性分析方法生成指定強度參數地震危險性曲線；

2)利用單變量地震重現期理論(式(6)或式(7))，生成指定場地單變量地震重現期。

2.2 雙變量地震重現期生成步驟

雙變量地震重現期可基于向量型概率地震危險性分析結果生成，生成步驟如下(流程圖如圖2所示)：

圖2 雙變量地震重現期計算流程圖Fig.2 Flowchart of bivariate earthquake return period calculation

1)基于場地危險性參數，采用向量型概率地震危險性分析方法(式(13)和式(14))，生成指定強度參數雙變量地震危險性曲面；

2)利用雙變量地震重現期理論(式(15))，生成指定場地雙變量地震重現期。

2.3 條件地震重現期生成步驟

條件地震重現期可以基于以下兩種方式得到：1)基于條件型概率地震危險性分析，直接得到條件地震重現期；2)基于標量型概率地震危險性分析，得到單變量地震重現期，基于向量型概率地震危險性分析，得到雙變量地震重現期，基于條件概率公式，得到條件地震重現期。

條件地震重現期方法1 生成步驟如下(流程圖如圖3(a))所示)：

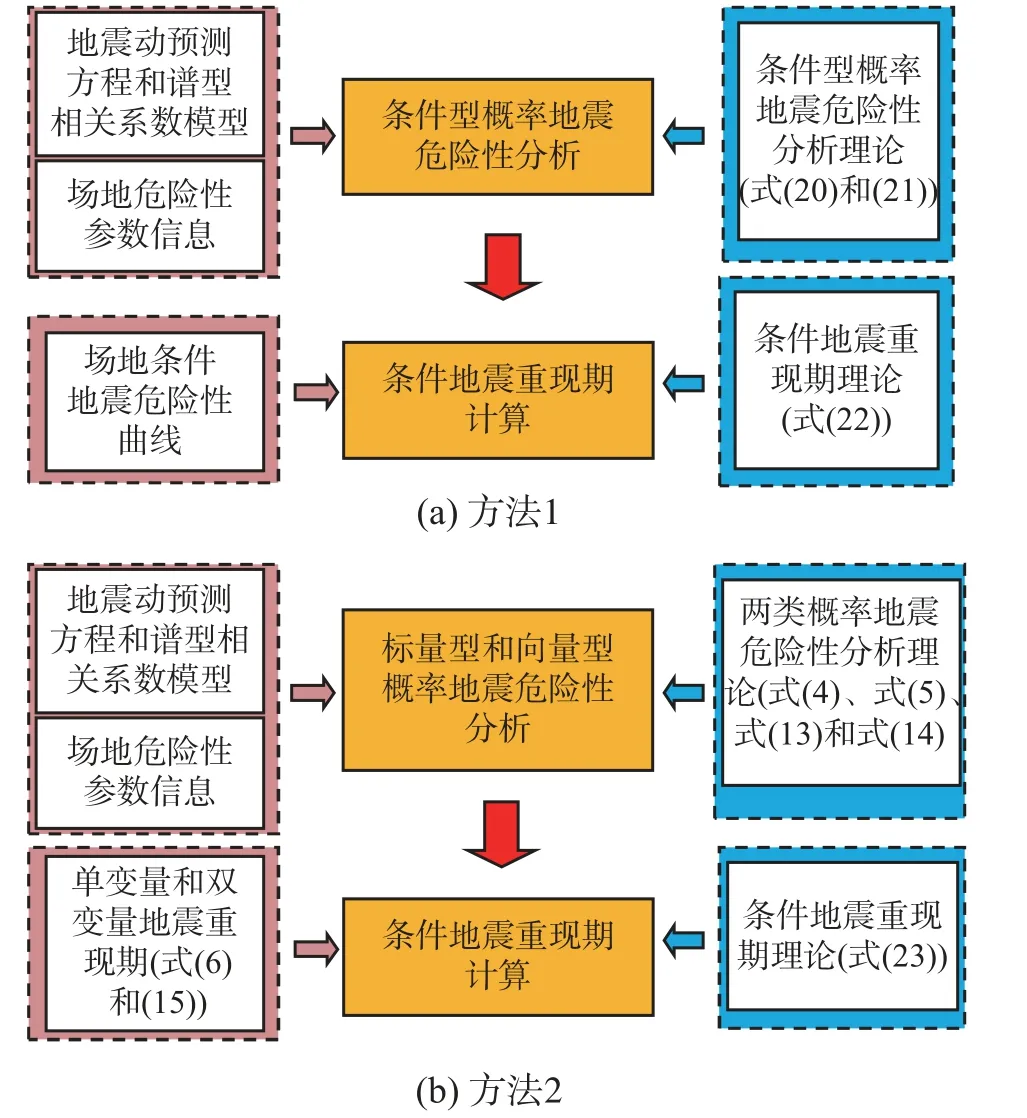
圖3 條件地震重現期計算流程圖Fig.3 Flowchart of conditional earthquake return period calculation

1)基于場地危險性參數信息，采用條件概率地震危險性分析方法(式(20)和式(21))，生成場地指定參數的條件概率地震危險性曲線；

2)利用條件地震重現期生成理論(式(22))，基于條件概率地震危險性曲線，生成指定場地條件地震重現期。

條件地震重現期方法2 生成步驟如下(流程圖如圖3(b))所示)：

1)基于場地危險性參數信息，采用標量型概率地震危險性分析(式(4)和式(5))，生成指定強度參數的標量型概率地震危險性曲線，利用單變量地震重現期生成理論(式(6)或式(7))，基于標量型概率危險性曲線，生成指定場地單變量地震重現期；

2)基于場地地震危險性參數信息，采用向量型概率地震危險性分析(式(13)和式(14))，生成指定強度參數的向量型概率地震危險性曲面，利用雙變量地震重現期生成理論(式(15))，基于向量型概率危險性曲面，生成指定場地雙變量地震重現期；

3)基于條件地震重現期理論(式(23))，利用生成的單變量地震重現期和雙變量地震重現期，得到條件地震重現期。

3 算例廠址地震重現期分析及應用研究

3.1 算例廠址地震危險性參數信息

本文以我國華南地區某核電廠廠址為算例廠址，基于場地危險性參數信息，利用單變量、雙變量和條件重現期分析理論，生成了算例廠址單變量、雙變量和條件重現期分布。該算例廠址包含一個地震統計區(覆蓋范圍N19°～N24°，E109°～E116°)，地震統計區參數如表1 所示。

表1 地震統計區參數值Table 1 Parameter values of seismic statistical zones

該統計區主要包括32 個潛在震源區(如圖4所示)。潛在震源區的主要參數包括：潛在震源區內最大震級、空間分布函數、方向角，上述三個參數及其相應權重取值詳見表2 所示。

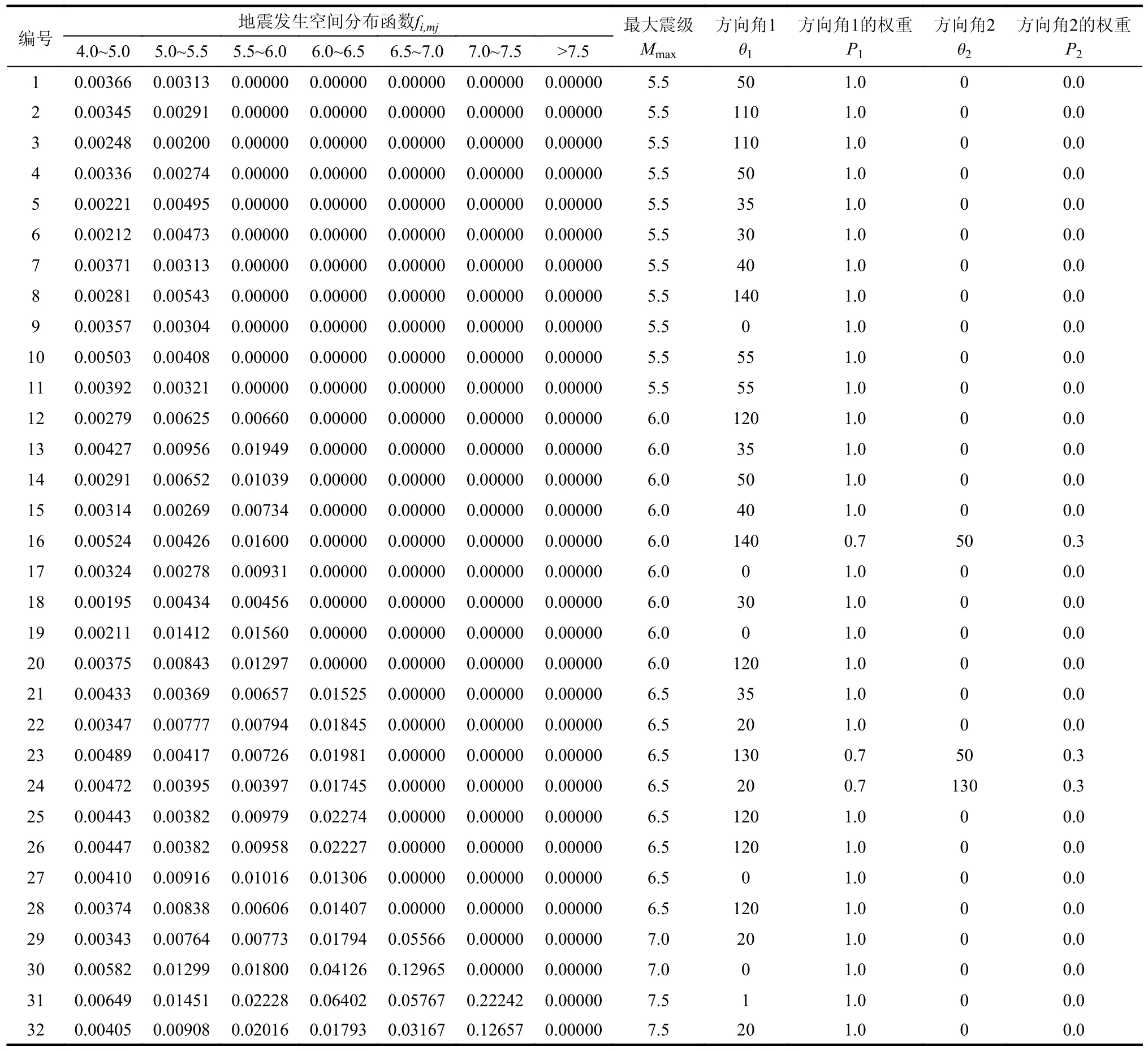
表2 潛在震源區地震活動性參數Table 2 Seismicity data of main potential sources of earthquake

圖4 潛在震源區分布圖Fig.4 Distribution map of seismic potential zones

地震動預測方程采用霍俊榮1989 年博士論文中給出的我國華南地區預測方程[22]，可表示為：

式中：M為震級；R為距離；ε為觀測誤差；σlog(Y)為預測方程的預測標準差；C1、C2、C3、C4和C5為地震動預測方程的系數，相關系數值參見文獻[22]。

3.2 算例廠址標量型概率地震危險性分析與單變量地震重現期分析

3.2.1 標量型概率地震危險性分析

本文選用具有代表性的一些強度參數，包括：PGA、Sa(0.07 s)、Sa(0.24 s)、Sa(0.50 s)、Sa(1.00 s)和Sa(5.00 s)，基于算例廠址場地危險性信息，采用標量型概率地震危險性分析方法，生成了算例廠址地震危險性曲線，如圖5 所示。可發現：不同強度參數地震危險性不同，與地震動預測方程中不同強度參數方程系數不同相關。

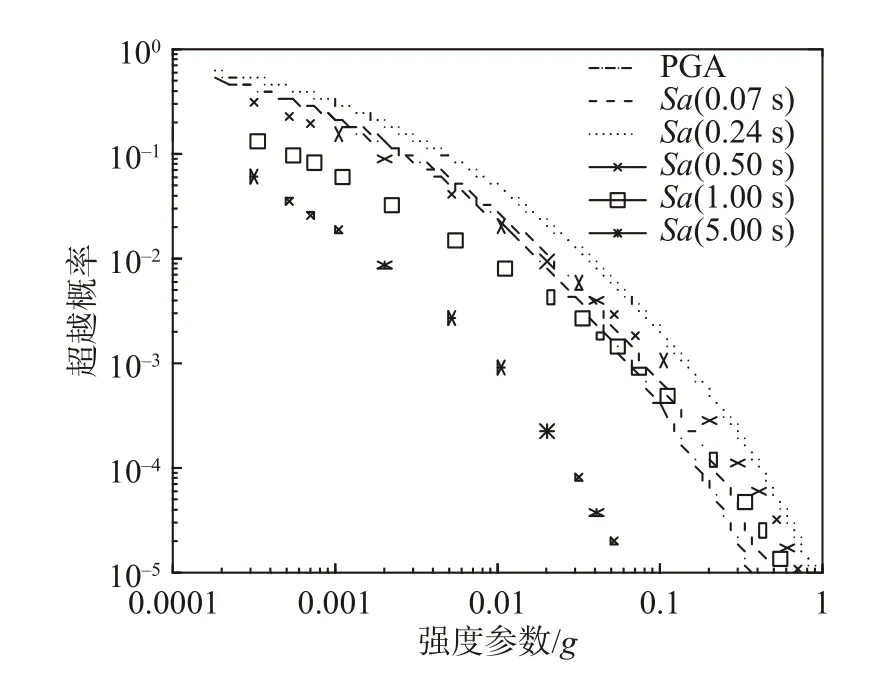
圖5 選定強度參數地震危險性曲線Fig.5 Seismic hazard analysis of selected intensity measures

3.2.2 單變量地震重現期生成

本文選用具有代表性的一些強度參數，包括：PGA、Sa(0.07 s)、Sa(0.24 s)、Sa(0.50 s)、Sa(1.00 s)和Sa(5.00 s)，基于生成的地震危險性曲線，利用式(6)，可得到算例廠址的不同地震動強度參數的單變量地震重現期，如圖6 所示。可發現：不同強度參數單變量地震重現期不同，與不同強度參數地震危險性大小不同相關。

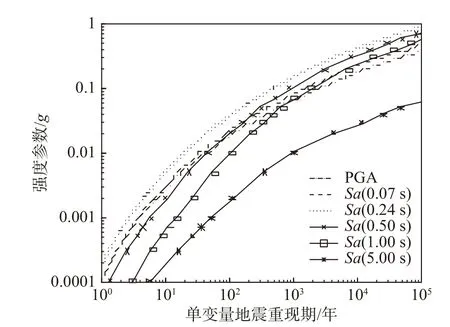
圖6 選定強度參數的單變量地震重現期Fig.6 Single variable earthquake return periods for selected intensity measures

3.3 算例廠址向量型概率地震危險性分析與雙變量地震重現期分析

3.3.1 向量型概率地震危險性分析

向量型危險性分析所用強度參數通常選取結構敏感周期的譜加速度，本文選用某結構[9]的基頻相應周期0.24 s 對應的譜加速度為雙強度參數中的一個參數，另外一個參數選用代表性的Sa(0.07 s)、Sa(0.50 s)、Sa(1.00 s)和Sa(5.00 s)與Sa(0.24 s)組合為雙強度參數，基于算例廠址場地危險性信息，采用向量型概率地震危險性分析方法，生成了算例廠址地震危險性曲面和危險性曲面等高線，如圖7～圖8 所示。分析結果表明：地震危險性曲面和等高線對于不同的強度參數組合結果不同，通常與兩個參數間相關性系數和強度參數危險性程度兩個因素相關。

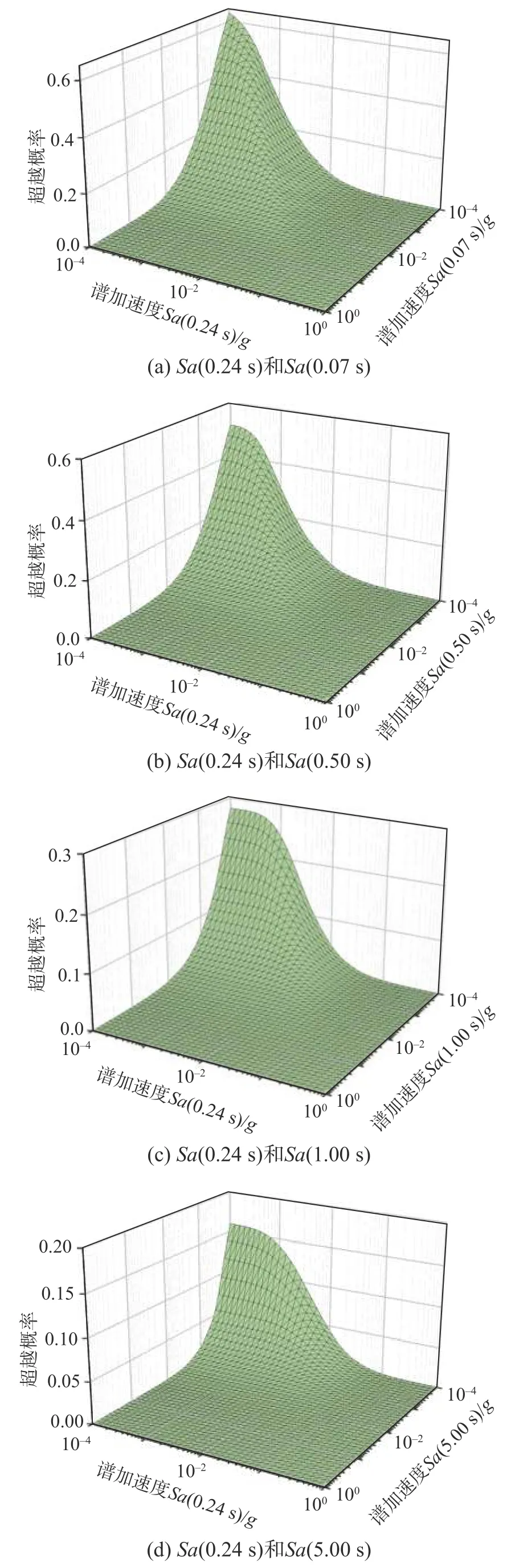
圖7 不同地震動強度參數組合的地震危險性曲面Fig.7 Seismic hazard surface based on combinations of different ground motion intensity measures

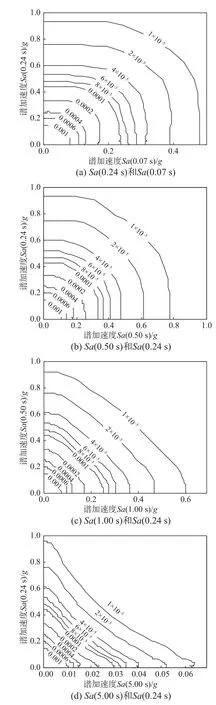
圖8 不同地震動強度參數組合的地震危險性曲面等高線Fig.8 Seismic hazard contours based on combinations of different ground motion intensity measures

3.3.2 雙變量地震重現期生成

基于生成的地震危險性曲面和等高線，利用式(15)，可得到算例廠址的不同地震動強度參數的雙變量地震重現期曲面和等高線，如圖9～圖10所示。分析結果表明：與向量型危險性分析結果類似，雙變量重現期曲面和等高線對于不同的強度參數組合結果不同，通常與兩個參數間相關性系數和強度參數危險性程度兩個因素相關。

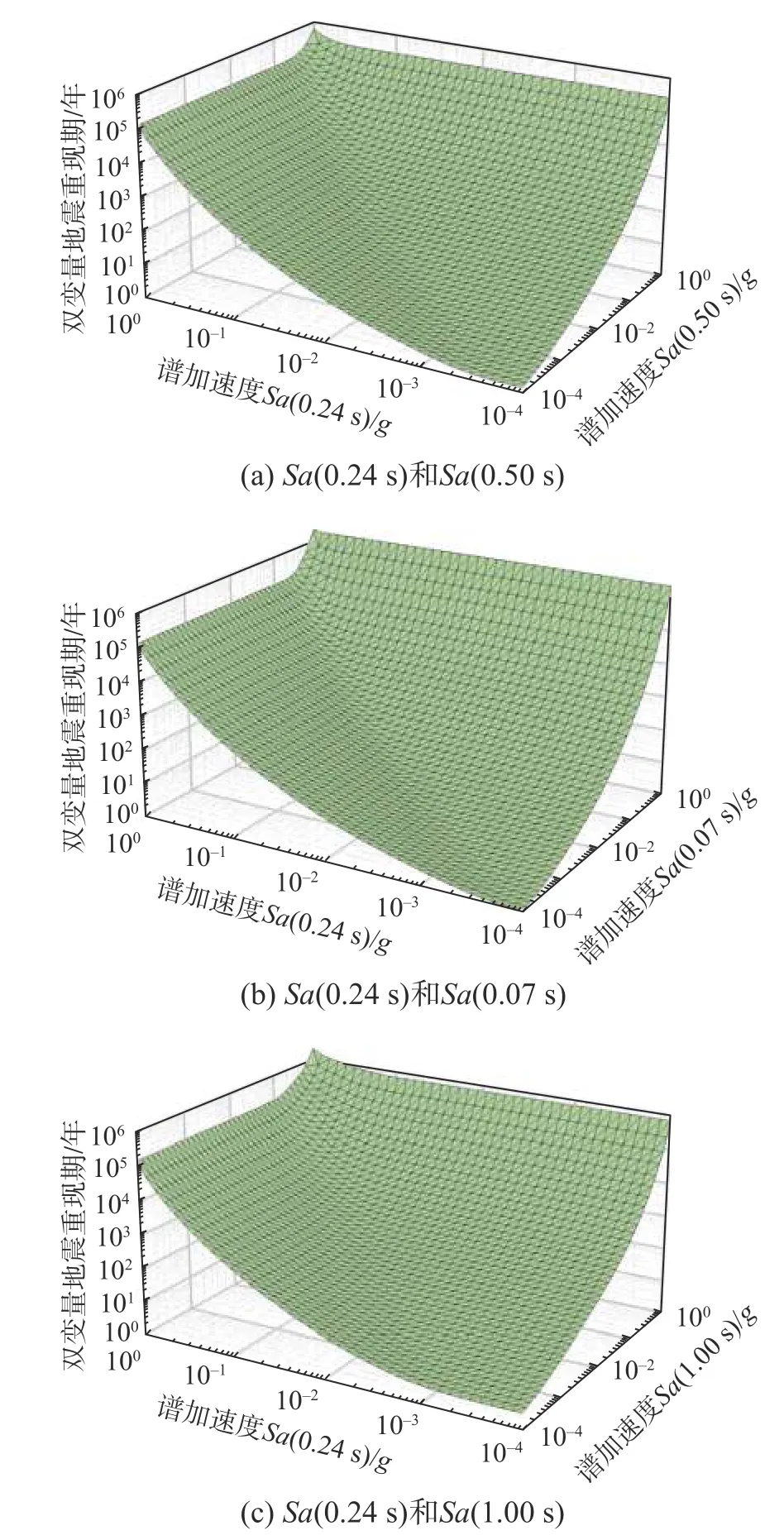
圖9 不同地震動強度參數組合的雙變量重現期Fig.9 Bivariate earthquake return period surface based on combinations of different ground motion intensity measures

圖10 不同地震動強度參數組合的雙變量重現期等高線Fig.10 Bivariate earthquake return period contours based on combinations of different ground motion intensity measures

3.4 算例廠址條件型概率地震危險性分析與條件地震重現期分析

3.4.1 條件型概率地震危險性分析

條件型危險性分析所用條件強度參數通常選取結構敏感周期的譜加速度，本文同樣選用某結構[9]的基頻相應周期0.24 s 對應的譜加速度為條件參數，另外一個預測參數分別選用Sa(0.07 s)和Sa(0.50 s)，基于算例廠址場地危險性信息，采用條件型概率地震危險性分析方法，生成了算例廠址條件地震危險性曲線，如圖11 所示。分析結果表明：條件強度參數越小，相同大小預測強度參數的超越概率越小。

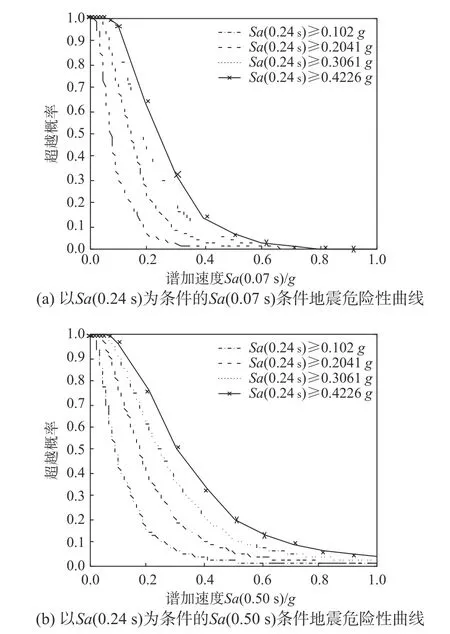
圖11 條件地震危險性曲線Fig.11 Conditional seismic hazard curves

3.4.2 條件地震重現期生成

基于生成的條件地震危險性曲線，利用式(22)，可得到算例廠址的不同地震動強度參數的條件地震重現期(Conditional Earthquake Return Period,CERP)，如圖12 所示。分析結果表明：條件強度參數越小，相同大小預測強度參數的條件地震重現期越大。

圖12 條件地震重現期Fig.12 Conditional earthquake return period

3.5 雙變量地震重現期與條件地震重現期應用研究

3.5.1 地震重現期在向量型場地相關譜生成中應用研究

近年來，針對一致危險譜的保守性，許多學者提出了條件均值譜概念，條件均值譜考慮了不同周期間譜型相關性，與真實地震動反應譜更為接近。但有學者指出，條件均值譜譜型較窄，可能會低估地震危險性水平，提出了多個條件參數的廣義條件均值譜概念。廣義條件均值譜的條件周期有兩個或兩個以上條件參數，本文僅分析兩個條件強度參數的廣義條件均值譜，該廣義條件均值譜也被稱為簡化廣義條件均值譜(Simplied Generalized Conditional Mean Spectra, s-GCMS)。文獻[9]曾提出了兩類簡化廣義條件均值譜概念，其中，第二類簡化均值譜(s-GCMS-II)需要運用雙變量地震重現期確定兩個條件強度參數的大小，第二類簡化均值譜(s-GCMS-II)具體生成步驟詳見文獻[9]。

基于算例廠址數據，生成算例廠址雙變量地震重現期，并得到算例廠址第二類簡化均值譜(s-GCMS-II)，算例廠址的一致危險譜(Uniform Hazard Spectrum，UHS)、條件均值譜(Conditional Mean Spectrum，CMS)和 第 二 類 簡 化 均 值 譜(s-GCMS-II)如圖13 所示。其中，第二類簡化均值譜需要運用雙變量地震重現期概念，Sa(0.07 s)和Sa(0.24 s)的雙變量地震重現期指定為10000 年。

圖13 算例廠址生成的場地相關譜Fig.13 Site-specific spectra of the case site

3.5.2 地震重現期在條件型場地相關譜生成中應用研究

利用條件概率地震危險性分析，可生成條件危險性曲線，基于條件地震重現期相等原則，可生成條件一致危險譜(Conditional Uniform Hazard Spectrum, CUHS)，CUHS 需要運用條件地震重現期概念[9]。

基于算例廠址數據，生成算例廠址條件地震重現期，并得到算例廠址相應于不同條件地震重現期的條件一致危險譜，見圖14 所示。

圖14 條件一致危險譜Fig.14 Conditional Uniform Hazard Spectra

其中，條件一致危險譜需要運用條件地震重現期概念，以Sa(0.24 s)為條件其它強度參數的條件地震重現期指定為2 年等。

4 結論和展望

本文對地震工程領域中地震重現期理論進行了深入研究，提出了雙變量地震重現期和條件地震重現期概念，給出了雙變量地震重現期和條件地震重現期理論基礎，總結了雙變量地震重現期和條件地震重現期生成步驟，生成了算例廠址的雙變量地震重現期和條件地震重現期，最后對雙變量地震重現期和條件地震重現期理論進行了應用研究，得出以下主要結論：

(1)基于向量型(雙變量)概率地震危險性分析(VPSHA)和條件型概率地震危險性分析(CPSHA)分析結果，可生成雙變量地震重現期和條件地震重現期；

(2) VPSHA 和CPSHA 在標量型概率地震危險性分析(PSHA)基礎上考慮地震動強度參數間相關性，使雙變量地震重現期和條件地震重現期在傳統單變量重現期基礎上考慮了地震動強度參數的相關性，可更科學考慮多個強度參數同時發生的聯合發生信息；

(3)提出了雙變量地震重現期和條件地震重現期概念，分析了三個地震重現期間關系，發現：指定參數雙變量地震重現期大于或等于兩個參數各自單變量地震重現期大小，條件地震重現期是雙變量地震重現期和單變量地震重現期之比；

(4)雙變量重現期曲面和等高線對于不同的強度參數組合結果不同，通常與兩個參數間相關性系數和強度參數危險性程度兩個因素相關；

(5)條件強度參數越小，相同大小預測強度參數的條件地震重現期越大；

(6)雙變量重現期和條件重現期可以運用在表示向量型(雙變量)場地相關譜和條件型場地相關譜生成研究中，傳統單變量重現期無法起到描述考慮譜型相關性信息重現期的作用。

未來需要在以下方面進行更進一步研究：

(1)深入開展多變量地震重現期及其條件地震重現期理論研究；

(2)深入開展基于多變量地震重現期和條件地震重現期理論的工程結構精細化地震易損性分析與風險評估研究；

(3)深入開展多變量地震重現期和條件地震重現期在工程結構抗震設計中的應用研究；

(4)深入開展考慮水平和豎向地震動強度參數相關性的雙變量地震重現期、多變量地震重現期和條件地震重現期理論與應用研究；

(5)深入開展考慮主震和余震地震動強度參數相關性的雙變量地震重現期、多變量地震重現期及其條件地震重現期理論與應用研究。