彈簧擺碰撞調諧質量阻尼器減震性能優化研究

王 奇，李宏男,2，張 鵬

(1.沈陽建筑大學土木工程學院，遼寧，沈陽 110168；2.大連理工大學土木工程學院，遼寧，大連 116024；3.大連海事大學交通運輸裝備與海洋工程學院，遼寧，大連 116023)

線性動力吸振器因其結構簡單、便于安裝而被廣泛用于結構的振動控制中[1?2]。為了提高線性吸振器的減振效果，學者們將多種形式的耗能、吸振組件引入其中，例如引入碰撞[3? 5]和內共振[6]。碰撞調諧質量阻尼器(pounding tuned mass damper,PTMD)是在懸掛質量擺(suspended mass pendulum,SMP)基礎上增設限位裝置，通過質量塊與限位器碰撞增加阻尼器的耗能能力。研究表明：PTMD的減震性能優于SMP，并且具有很好的魯棒性[7?9]。彈簧擺(spring pendulum, SP)是用彈簧替代了SMP的擺線，依靠彈簧內共振增加阻尼的吸振能力[10]。在本文作者的工作中[11]，將碰撞阻尼與彈簧擺相結合，提出了一種新型非線性阻尼器，即彈簧擺碰撞調諧質量阻尼器(spring pendulum pounding tuned mass damper, SPPTMD)。SPPTMD 由彈簧擺及限位裝置構成，通過彈簧內共振及質量塊與限位器碰撞耗能。研究結果表明：SPPTMD 具有良好的減震效果。

在振動控制系統的設計中，減振裝置的參數及布置位置的選取對減振效果的影響很大[12?13]，對這些變量進行優化是很有必要的。智能優化算法根據原理不同可分為三類：基于生物學原理的優化算法、基于物理學原理的優化算法和其他類型的優化算法[14]。基于生物學原理的優化算法是對生物進化行為的模擬，包括遺傳算法、人工魚群算法、螢火蟲算法和粒子群算法等。GRECO 等[15]利用遺傳算法，以建設成本和減振率為優化目標，對阻尼器進行了優化。金波等[16]基于改進遺傳算法對粘滯阻尼器的位置及數量進行了優化。張曉峰等[17]和周紅杰等[18]分別采用人工魚群算法和多島遺傳算法，對用于漂浮式風力機振動控制的TMD 參數進行了優化。龍關旭等[19]通過螢火蟲算法和模擬退火算法，對用于大跨斜拉橋振動控制的阻尼器參數進行了優化。王小金等[20]采用粒子群算法對用于高層結構減振的TMD 參數進行了優化。基于物理學原理的優化算法包括模擬退火算法和混沌優化算法等。賴文龍等[21]提出了基于模擬退火算法的阻尼器位置優化。KAVEH 等[22]采用混沌優化算法優化了TMD 的參數。其他算法包括和聲搜索算法、差分進化算法等。NIGDELI和BEKDA?[23]采用和聲搜索算法，以結構頂層加速度傳遞函數最小為優化目標函數，對TMD 的質量、周期和阻尼系數進行了優化。LE-DUC 等[24]將差分進化算法與無梯度全局優化算法結合，對各種類型的磁流變阻尼器參數進行了優化。上述研究均表明，對減振裝置進行優化設計能有效地提高其抑振性能。

盡管已有研究表明：SPPTMD 具有較好的減震性能，但其設計參數(包括頻率比、彈簧內共振系數、碰撞間隙等)尚需進一步優化設計才能達到更好的減震效果。

粒子群算法適合在動態、多目標優化環境中進行尋優計算。與眾多優化算法相比，粒子群算法需要調整的參數較少，算法結構簡單，并且具有更高效的并行計算能力，可以在較短時間搜尋到全局最優[25?26]。另外，粒子群算法對種群數量變化不是十分敏感，尋優性能穩定[27?28]。因此，本文采用魯棒性強并且收斂快的粒子群算法，對SPPTMD 的參數進行優化。以結構最大位移最小為目標函數，并且選取多條地震動驗證了優化后SPPTMD 的減震性能。

1 結構-SPPTMD 系統模型

1.1 SP 減振機理

SP 可認為是一種改進的SMP，即用彈簧代替擺線。SP 具有兩種圓頻率：徑向振動模式圓頻率ωs和擺動振動模式圓頻率ωp(圖1[11])。

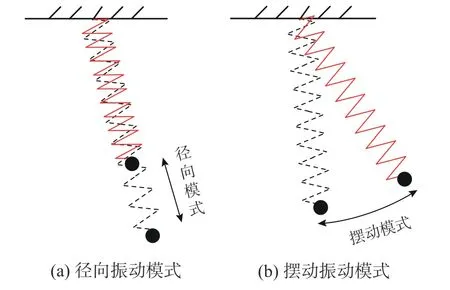
圖1 SP 的振動模式Fig.1 Vibration modes of the SP

研究發現[29]，當滿足特定條件時，兩種振動模式將強烈耦合，振動能量會在兩種振動模式之間不斷傳遞，被稱為內共振現象，根據內共振條件可得彈簧剛度為：

式中：ks為彈簧的剛度；為彈簧內共振系；md為質量塊的質量；g=9.8 m/s2為重力加速度；lo為彈簧在重力作用下的長度：

式中：f為主結構頻率；為阻尼器頻率比。

內共振現象將放大SP 的動力吸振能力，相比于懸掛質量擺，滿足內共振時SP 的減振效率更高。然而，已有SP 仍存在耗能能力不足問題，故引入碰撞耗能模式，提出了彈簧擺碰撞調諧質量阻尼器(SPPTMD)。

1.2 SPPTMD 減振機理

SPPTMD 是在SP 的基礎上增設限位器(如圖2所示[11])，它是依靠SP 及附加質量與限位器碰撞來耗能的非線性吸振器。在結構振幅較小時，附加質量與限位器沒有發生碰撞，SPPTMD 退化為傳統SP；當結構振幅較大時，附加質量與限位器發生碰撞，此時SPPTMD 通過撞擊消耗阻尼器吸收的系統動能。

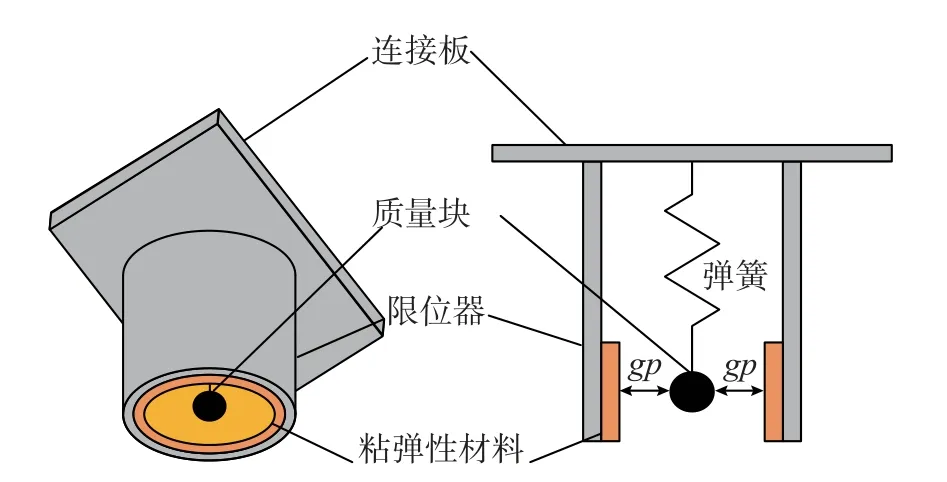
圖2 SPPTMD 示意圖Fig.2 Schematic of the SPPTMD

1.3 結構-SPPTMD 系統模型的建立

假設，SPPTMD 附加在一個n自由度體系的第i個自由度上(如圖3 所示[11])，則結構-SPPTMD體系的運動方程為：

圖3 第i 個自由度上的控制力Fig.3 Controlling forces imposed on the i-th DOF

式中：Ms、Cs和Ks分別為無控結構的質量矩陣、阻尼矩陣和剛度矩陣；x¨(t) 、x˙(t) 和x(t)分別為無控結構的加速度、速度和位移；I為1 的列向量；x¨g為 地 面 加 速 度；L為SPPTMD 的 位 置 向 量；Fs,x和Fc,x分別為附加質量在x方向的恢復力和碰撞力；Fdir為碰撞力方向；xd和yd分別為質量塊在水平和垂直方向的位移；Fs,y和Fc,y分別為附加質量在y方向的恢復力和碰撞力。SPPTMD 的位置向量L可寫成：

由于限位器是環形的，左右兩側都能發生碰撞。碰撞力方向Fdir為：

根據之前的研究，可以得恢復力和碰撞力的公式：

式中：xi為無控結構第i個自由度的水平方向的位移；lori為彈簧原長。

假設質量塊與邊界的間距是gp，根據Hertz 接觸單元和非線性阻尼的碰撞力模型可得SPPTMD的碰撞力為[30]：

式中：β為碰撞剛度；δ為粘彈性材料的相對變形；c為碰撞阻尼。δ和c可由下面2 個公式計算：

式中：ξ為碰撞阻尼比；mi為無控結構第i個自由度的質量。ξ可由下式計算:

2 粒子群算法的優化過程

為解決SPPTMD 參數優化問題，本文以結構最大位移最小為優化目標，以SPPTMD 阻尼比、內共振系數和碰撞間隙為優化變量，采用粒子群算法進行優化設計。粒子群算法最早是由KENNEDY和EBERHART[31]提出的，其基本思想是：每個粒子將其在空間中搜尋到的最優解記為個體極值，將粒子的個體極值在粒子群中共享，找到整個粒子群當前的最優解，并將其記為當前全局最優解。每個粒子根據當前的個體極值及全局最優解來調整粒子的速度和位置，直到找到全局最優解。

粒子群尋優過程如圖4 所示：

圖4 優化流程圖Fig.4 Optimization flow chart

步驟1：初始化粒子群，例如設置粒子群規模、慣性因子、學習因子、優化變量初始值、粒子群更新速度、最大迭代次數；

步驟2：根據目標函數，計算每個粒子的適應度值，尋找個體極值；

步驟3：粒子間共享個體極值，找到當前粒子群的全局最優解；

步驟4：每個粒子根據當前速度、位置、和全局最優值調整下一步的速度和位置；

步驟5：不斷的迭代尋找全局最優值；

步驟6：保存全局最優值及最優參數，尋優過程結束。

本文將有控和無控結構頂點最大位移的比值最小作為優化目標，目標函數為：

式中，D0和D1分別為結構在無控和有控時的頂點最大位移。

3 數值算例分析

3.1 工程實例

以某53.9 m 高的輸電塔為振動控制研究對象。如圖5 所示，輸電塔被簡化為15 個自由度，一階頻率為 1.87 Hz。為了說明優化方法的有效性，本文將優化前、后SPPTMD 的減震效果進行了比較。其中，定義未優化的SPPTMD 頻率比為1，質量比為3%，內共振系數為2，碰撞剛度為17 000 N/m3/2，碰撞間隙為0.05 m，SPPTMD 通過螺栓連接到輸電塔的頂部。對SPPTMD 的頻率比、內共振系數和碰撞間隙進行優化，使結構頂點位移最小。

圖5 輸電塔示意圖Fig.5 Schematic of the transmission tower

定義減震率為：

3.2 地震動選取

為了優化SPPTMD 在I 類、II 類、III 類、IV 類場地中的減震性能，每類場地選取了3 條地震動進行研究，峰值加速度調整為400 cm/s2，地震記錄相關信息如表1 所示，反應譜曲線如圖6 所示。

表1 地震記錄Table 1 Seismic records

圖6 加速度反應譜Fig.6 Acceleration response spectrum

3.3 結果分析

優化結果如表2 所示，表3 列出了結構峰值位移減震情況，由于所選取的地震動較多，文中只給出了4 條地震動作用下結構的位移響應(如圖7、圖8 所示)。

表2 最優參數Table 2 Optimal parameters

表3 減震率Table 3 Vibration reduction ratios

圖7 地震動作用下結構位移時程曲線Fig.7 Displacement time history of the structure under the seismic

圖8 地震動作用下結構位移包絡圖Fig.8 Envelope of displacement of the structure under the seismic

從計算結果可以看出，任何工況下SPPTMD減震率均在36%以上。未優化的SPPTMD 在I 類、II 類、III 類、IV 類場地中的峰值減震率的均值都在40%以上，分別為40.52%、41.96%、43.17%和49.34%，其中IV 類場地中的減震率比I 類場地增加了8.82個百分點。優化后的SPPTMD峰值減震率的均值都在48%以上，分別為48.77%、52.02%、53.41%和62.17%，其中IV 類場地中的減震率比I 類場地增加了13.4 個百分點。

與優化前相比，I 類～IV 類場地中SPPTMD減震率均值分別提高了8.25、10.06、10.24 和12.84個百分點。可見，SPPTMD 的振動控制性能隨著場地類別的提升而提升；優化后，SPPTMD 在IV 類場地中的抑振性能提高的幅度最大。綜上所述，編制的優化程序能夠有效優化SPPTMD 的參數，提升阻尼器的減震性能。

4 結論

為了提高SPPTMD 的振動控制性能，采用粒子群算法對SPPTMD 參數進行了優化，并研究了不同場地地震動作用下SPPTMD 的減震效果，得出了以下主要結論：

(1)對不同場地類別的結構進行振動控制時，SPPTMD 的最優參數也不同，且存在如下規律：場地類別越堅硬，頻率比越低，內共振系數越大。

(2) 場地土越軟弱SPPTMD 的振動控制性能越好，I 類場地減震率最低，IV 類場地減震率最高。

(3)優化后，SPPTMD 減震率有大幅提高，減震率均值最高可達60%，說明編制的優化程序能夠有效優化SPPTMD 的參數。