反彈對撞式沖擊放大器機理研究

武雙雙，金映麗，閆 明，顧西平

(沈陽工業大學機械工程學院，沈陽 110870)

隨著新興技術的快速發展，電子設備逐漸趨于小型化。其中，MEMS(Micro electro mechanical system)器件與集成電路相比具有明顯的優勢，由于質量小、結構緊湊且易于封裝等特點，通常用于可靠性非常高的電信設備、導彈控制系統的關鍵零部件、智能彈藥等，要求其必須能夠在極其惡劣的沖擊環境下可靠的工作[1]。然而，MEMS 器件的可靠性工程仍處于起步階段，尤其是部署在惡劣沖擊環境中的微器件，難免會受到可能導致應力相關故障的沖擊激勵[2]。目前，MEMS 器件上常用的高加速度測試方法主要有軌道炮、氣槍、自由落體實驗、霍普金森桿及半正弦沖擊機等[3]。但因存在尺寸大、成本高、安全性及可重復性差等缺陷而應用不廣。因此，對在傳統跌落沖擊試驗臺上實現沖擊放大的方法展開研究具有重要意義。

早在20 世紀六七十年代，國外已對多質量碰撞沖擊放大方法進行了研究。HART 等[4]和HARTER[5]先后研究了多質量一維碰撞中連續物體質量比對碰撞的影響規律。RODGERS 等[6]研究了多質量成對碰撞的速度放大動力學，提出基于簡單多剛體動力學確定中間物體數量和質量的理論依據，分析了質量比和碰撞恢復系數對速度放大的影響。O’DONOGHUE 等[7]利用多質量碰撞理論產生的速度放大效應對速度放大電磁發生器展開研究，增加質量比和質量數可有效實現速度放大。DUAN 等[8]基于雙質量疊加碰撞，提出一種結構簡單且有效的沖擊機，用于模擬高加速度沖擊環境。KELLY 等[9]為了實現小規模和可重復的高加速度脈沖，研究了一種用于MEMS 高加速度沖擊測試的速度放大器，但僅將速度放大作為沖擊放大的衡量指標。ANDY[10]基于經典碰撞理論對DMSA (Dual mass shock amplifier)的放大過程進行分析與建模，研究了不同參數對二次碰撞速度和加速度的影響。但未考慮二次碰撞過程中的能量損失，導致模型預測的速度變化及加速度值遠遠高于試驗測量值。BERGLUND[11]改進了一種沖擊放大器，用于單軸壓縮中SIFCON 的高應變率測試。DOUGLAS 等[12?13]研究了由DMSA 產生的高加速度對PWB (Printed wiring board)的影響，提供了從簡單的解析閉合形式剛體力學到詳細的非線性動態有限元分析的模型，通過參數化建模，研究了不同設計參數對加速度的影響。但僅采用動態接觸理論進行建模，且未考慮碰撞過程中系統的能量損失。LALL 等[14?15]通過DMSA 提供加速度脈沖，對圓形印刷電路板進行試驗，研究了不同沖擊角度及輔助約束機制對其在高加速度環境下可靠性的影響。

以上文獻對DMSA 進行了不同程度的研究。其中，關于整個沖擊放大過程的理論研究較少，且建模時忽略了能量損失等影響因素，不符合實際情況。本文采用經典碰撞理論與動態接觸理論相結合的方法，引入碰撞恢復系數(考慮能量損失)，建立了反彈對撞式沖擊放大器運動學模型，理論上推導出沖擊放大臺加速度及其放大倍數計算公式，研究了預留間隙、彈力繩剛度對二次碰撞加速度響應的影響，并通過沖擊試驗對理論模型進行了驗證。

1 反彈對撞式沖擊放大器裝置

1.1 工作原理

反彈對撞式沖擊放大器的工作原理為：基于自由落體獲得初始速度，利用跌落臺首次撞擊基座波形發生器后跌落臺的反彈速度作為沖擊激勵載荷，作用于沖擊放大器，使放大臺獲得更大的加速度響應。系統結構如圖1 所示。

圖1 反彈對撞式沖擊放大器裝置Fig.1 Rebound collision type shock amplifier device

反彈對撞式沖擊放大器底座固定在跌落臺上，隨跌落臺做自由落體運動。當跌落臺與基座波形發生器碰撞(一次碰撞)后反彈向上運動。此時，放大臺由于慣性在彈力繩的作用下繼續向下運動，與反向運動的跌落臺發生二次碰撞。由于放大臺質量遠小于跌落臺質量，使得放大臺產生很大的速度改變；又因二次碰撞時間極短，導致產生了遠遠大于一次碰撞的沖擊加速度。

1.2 結構模型

沖擊放大器結構如圖2 所示，主要由底座、導向柱、彈力繩、橫梁、橡膠波形發生器、放大臺、緩沖圈及其它附屬部件組成。其中，緩沖圈主要用來吸收碰撞過程中的能量，改善多次碰撞問題；放大臺用來放置被測物體；改變波形發生器厚度可調節碰撞的持續時間；彈力繩用來平衡放大臺的重力，使其懸浮；導向柱保證沖擊放大器隨沖擊試驗臺沿垂向運動。

圖2 沖擊放大器結構圖Fig.2 Structure of shock amplifier

2 運動學模型分析

反彈對撞式沖擊放大器隨跌落臺從高度h處開始做自由落體運動，與基座波形發生器發生一次碰撞。假定豎直向上為正方向，考慮碰撞過程中的能量損失，由動量守恒可得：

式中：m0為基座質量；m1為跌落臺質量；v0為一次碰撞前基座速度且v0=0 m/s；v1為一次碰撞前跌落臺速度且，g為重力加速度，h為跌落高度；為一次碰撞后基座速度；為一次碰撞后跌落臺速度；e1為跌落臺與基座的碰撞恢復系數，取值范圍為0～1。聯立式(1)、式(2)可得：

式中，?v1為一次碰撞中跌落臺的速度變化量。

由于基座波形發生器為半正弦波形發生器(表面有凸起)，產生的波形近似為半正弦波。假設碰撞產生的波形為理想半正弦，則一次碰撞后跌落臺的加速度為：

式中，?t1為一次碰撞過程中的碰撞持續時間。

記從一次碰撞開始到放大臺與跌落臺碰撞(二次碰撞)前的運動位移為s1，運動時間為?t1+t2。由機械運動學知識可知，該運動過程可簡化為單自由度彈簧質量系統，可得：

式中：

式中：v2為一次碰撞前放大臺速度，且滿足v2=v1=；k3為單根彈力繩剛度，彈力繩總數為4 根。

記跌落臺反向向上運動與放大臺碰撞前跌落臺的位移為s2，運動時間為t2，由勻變速直線運動可知：

當跌落臺與放大臺發生二次碰撞時，跌落臺向上運動位移與放大臺向下運動位移之和為初始時放大臺與底座之間的距離，即滿足：

式中，d為初始時放大臺和底座之間的距離，稱為預留間隙。

聯立式(6)～式(9)可得：

由于整個碰撞過程極其短暫(毫秒級)，?t1+t2趨近于零，則式(10)可改寫為：

整理可求得t2為：

則二次碰撞前跌落臺的速度為：

放大臺速度為：

為了獲得較高的加速度峰值，假設二次碰撞發生在一次碰撞結束的瞬間，則該碰撞過程的運動學方程為：

式中：m2為放大臺質量；為二次碰撞前跌落臺速度；為二次碰撞前放大臺速度；為二次碰撞后跌落臺速度；為二次碰撞后放大臺速度；e2為跌落臺與放大臺的碰撞恢復系數，取值范圍為0～1。由式(15)可得：

由于底座安裝的波形墊是圓形橡膠平墊(表面無凸起)，產生的波形類似于三角波。假設跌落臺與放大臺碰撞產生的波形為理想三角波，則二次碰撞放大臺加速度為：

由于m0>>m1，m1>>m2，將式(3)、式(12)～式(14)代入式(18)可得：

結合式(5)可得加速度放大倍數n為：

式中，?t2為跌落臺與放大臺碰撞中的持續時間。

以上是涉及經典碰撞接觸理論[10,16 ? 19]的研究內容，假設碰撞接觸是瞬間完成的，以碰撞恢復系數表示碰撞前后的速度變化。而動態接觸理論[12]則認為碰撞接觸過程是連續的，充分考慮碰撞過程中的接觸變形和接觸力的變化。

為了更準確的描述碰撞接觸的過程，結合動態接觸理論，將跌落臺與基座的碰撞過程簡化為單自由度彈簧-質量系統，跌落臺與放大臺的碰撞過程簡化為雙自由度彈簧-質量系統。通過求解單自由度、雙自由度彈簧-質量系統，可得一次碰撞持續時間?t1、二次碰撞持續時間?t2分別為：

式中：k1為基座波形發生器剛度；k2為沖擊放大器底座波形發生器剛度。

由圓柱形橡膠波形發生器剛度公式可得：

式中：k為橡膠波形發生器剛度；N為橡膠材料沖擊剛度與靜剛度比值，由文獻[20]可知N取值范圍為1～3，本文N取2.5；E為橡膠波形發生器彈性模量；A為橡膠波形發生器橫截面積；r為橡膠波形發生器厚度。結合式(23)可求得k1和k2：

式中，HS 為橡膠的硬度值。

將式(21)代入式(19)、式(20)可得：

由式(24)、式(25)可知，放大臺的加速度及其放大倍數與跌落高度h、彈力繩剛度k3、預留間隙d、跌落臺質量m1、放大臺質量m2、波形發生器剛度k1、k2及碰撞恢復系數e1、e2等均有關，它們之間的關系是非線性的。這里將放大臺的加速度作為沖擊放大效果的衡量指標，以下僅對預留間隙d、彈力繩剛度k3兩個主要參數對沖擊放大效果的影響展開理論性分析。

2.1 預留間隙對沖擊放大效果的影響

在沖擊激勵下，放大臺加速度與預留間隙主要存在以下3 種關系：

1)當預留間隙等于零，即d=0 時，放大臺與跌落臺處于臨界接觸狀態，未發生連續碰撞，此時不具有沖擊放大效應。

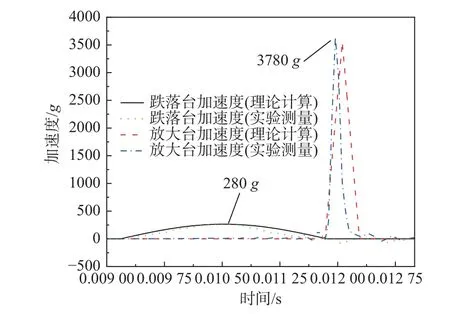
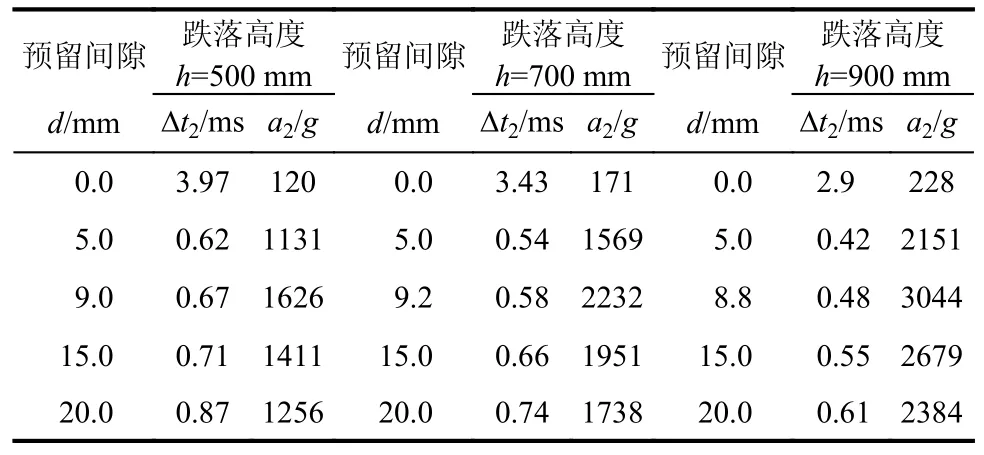
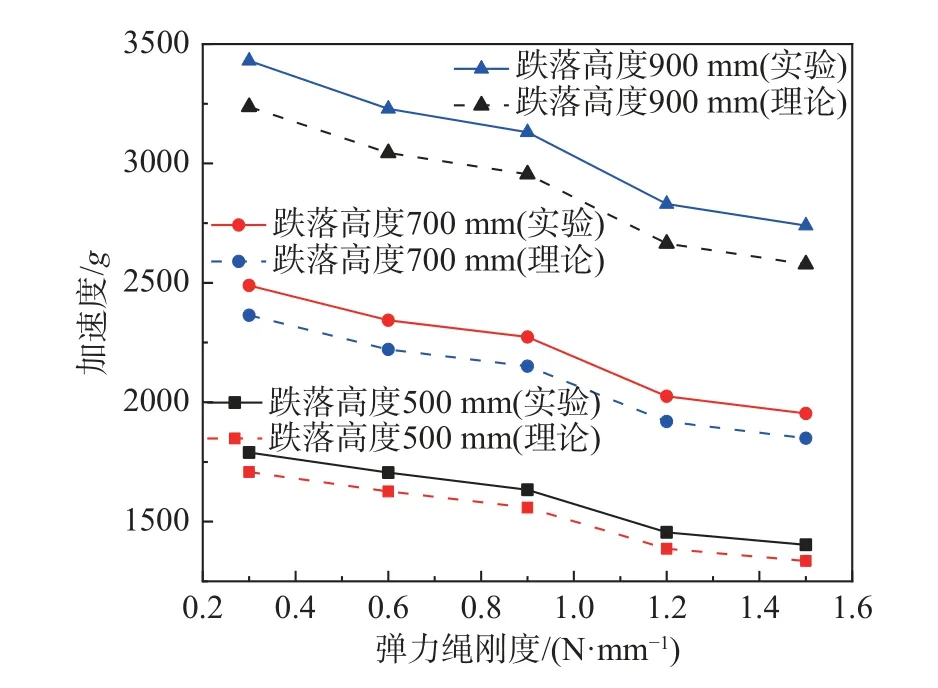
2)當預留間隙小于理想預留間隙，即d

若二次碰撞發生在一次碰撞壓縮階段，則放大臺加速度與預留間隙之間的關系式為：

若二次碰撞發生在一次碰撞回彈階段，則放大臺加速度與預留間隙之間的關系為：

式中：?t1lx為在理想預留間隙下跌落臺與基座的碰撞持續時間；dlx為理想預留間隙。

由式(26)可知，在跌落高度一定下，當預留間隙小于理想預留間隙時，若二次碰撞發生在一次碰撞壓縮階段，放大臺加速度隨預留間隙的增加逐漸減小，二者呈負相關。由式(27)可知，若二次碰撞發生在一次碰撞回彈階段，放大臺加速度隨預留間隙的增加逐漸增加，二者呈正相關。

3)當預留間隙等于理想預留間隙，即dlx/v1=?t1lx時，放大臺加速度理論計算公式為：

由式(28)可知，當預留間隙為理想預留間隙時，放大臺加速度幅值最大。

4)當預留間隙大于理想預留間隙，即d>dlx時，放大臺加速度理論計算公式見式(19)，即：

由式(29)可知，在跌落高度及彈力繩剛度等參數一定下，當預留間隙大于理想預留間隙時，放大臺加速度隨預留間隙的增加逐漸減小，二者呈負相關。綜上，為了達到最佳的沖擊放大效果，應將預留間隙盡量保持在理想預留間隙附近。

2.2 彈力繩剛度對沖擊放大效果的影響

為了計算簡便，假定彈力繩剛度是恒定的，即滿足胡克定律。實際情況下，放大臺在彈力繩的拉力作用下，速度略有減少，放大臺與跌落臺碰撞前的實際速度為：

假設預留間隙為理想預留間隙，則放大臺加速度與彈力繩剛度的關系見式(28)。由式(28)可知，當跌落高度一定時，放大臺加速度隨彈力繩剛度的增加逐漸減小。因此，在沖擊放大裝置的設計中，理論上可選取較小彈力繩剛度，以提高沖擊放大效果。

3 反彈對撞式沖擊放大方法實驗驗證

為了驗證反彈對撞式沖擊放大方法理論計算的正確性，設計如圖2 所示的實驗裝置，實驗整體布局如圖3(a)所示，電源線接頭強沖擊實驗布置如圖3(b)所示。分別對預留間隙、彈力繩剛度對放大臺加速度的影響展開研究。

圖3 實驗裝置布局方式Fig.3 Layout of experimental equipment

已知跌落臺質量為410 kg，放大臺質量為6 kg，基座橡膠波形發生器硬度為90，半徑為100 mm，厚度為10 mm，底座橡膠波形發生器硬度為80，半徑為75 mm，厚度為5 mm。由于跌落沖擊試驗機底座傾斜及導桿與跌落臺之間存在較大摩擦，故實際重力加速度小于理論重力加速度，經試驗測量取0.53g。由于沖擊試驗機底座的空氣彈簧和液壓阻尼緩沖器的作用，跌落臺與基座碰撞時能量損失較大，導致e1相對于e2偏小，實驗測得碰撞恢復系數e1=0.4，e2=0.72。實驗過程中的加速度曲線如圖4 所示。

圖4 跌落高度h=1000 mm 加速度時間曲線Fig.4 Acceleration time curve with drop height h=1000 mm

由圖4 可知，在跌落高度為1000 mm 下，當預留間隙為10 mm 時，跌落臺加速度波形接近于理想半正弦波，放大臺的加速度波形接近于理想三角波，驗證了理論假設的正確性。實驗測得跌落臺加速度幅值約為280g，放大臺加速度幅值約為3780g，加速度放大約13.5 倍。跌落臺與基座碰撞持續時間?t1為2.68 ms，放大臺與跌落臺碰撞持續時間?t2為0.44 ms。理論計算放大臺加速度誤差為7%左右，滿足誤差要求，故理論計算與實驗結果具有較好的一致性。

3.1 預留間隙對放大臺加速度的影響

分別選取500 mm、700 mm 和900 mm 三種跌落高度，研究放大臺加速度隨預留間隙變化的規律。其中，當跌落高度為500 mm 時，v1=2.28 m/s，?t1=3.97 ms；當跌落高度為700 mm 時，v1=2.7 m/s，?t1=3.43 ms；當跌落高度為900 mm 時，v1=3.06 m/s，?t1=2.90 ms，取預留間隙9.0 mm，9.2 mm，8.8 mm為理想預留間隙。不同預留間隙下的加速度理論計算結果見表1，理論與試驗結果的對比如圖5 所示。

表1 不同預留間隙下加速度理論計算值Table 1 Theoretical calculation of acceleration under different elastic drop gaps

圖5 預留間隙對加速度幅值的影響Fig.5 Influence of drop gap on peak acceleration

由表1 及圖5 可知，當跌落高度一定時，放大臺加速度隨預留間隙的增加先增大后減小，即存在一個理想預留間隙，使放大臺加速度取最大值。當預留間隙小于理想預留間隙時，二次碰撞發生在一次碰撞期間，跌落臺與放大臺碰撞時速度(一次碰撞后的回彈)未恢復到最大，導致二次碰撞的加速度較小；隨著預留間隙向理想預留間隙靠近，跌落臺的速度隨之增加，二次碰撞的加速度也逐漸增大；當預留間隙等于理想預留間隙時，跌落臺速度達到最大，此時產生的加速度也最大；當預留間隙大于理想預留間隙時，放大臺開始做勻減速直線運動，速度減小，此時二次碰撞的加速度也逐漸減小。

當跌落高度為900 mm 時，理想預留間隙為8.8 mm，放大臺加速度理論計算值為3044g，試驗測量值為3220g，相對誤差為5.5%，滿足誤差要求。且同一預留間隙下，跌落高度越大，放大臺加速度增加越明顯。因此，在沖擊機跌落高度的允許范圍內，可盡量選取理想預留間隙及較大的跌落高度，以獲得更高的沖擊加速度。

3.2 彈力繩剛度對放大臺加速度的影響

分別選取500 mm、700 mm 和900 mm 三種跌落高度，調節預留間隙為理想預留間隙，研究放大臺加速度隨彈力繩剛度變化的規律。其中，當跌落高度為500 mm 時，v1=2.28 m/s，?t1=3.97 ms；當跌落高度為700 mm 時，v1=2.7 m/s，?t1=3.43 ms；當跌落高度為900 mm 時，v1=3.06 m/s，?t1=2.90 ms。不同彈力繩剛度下的加速度理論計算結果見表2，理論與試驗結果的對比如圖6所示。

表2 不同彈力繩剛度下的加速度理論計算值Table 2 Theoretical calculation of acceleration under different elastic rope stiffness

圖6 彈力繩剛度對加速度的影響Fig.6 Influence of elastic rope stiffness on acceleration

由表2 及圖6 可知，當跌落高度一定時，隨著彈力繩剛度增加，放大臺加速度幅值逐漸減小。主要原因是隨著彈力繩剛度的增加，放大臺與跌落臺碰撞時的速度逐漸減小，導致二次碰撞過程中放大臺的速度變化量也變小，進而產生的加速度也逐漸減小。當跌落高度為900 mm 時，彈力繩剛度由0.3 N/mm 增加到1.5 N/mm，放大臺加速度理論計算值由3237g逐漸減小到2578g，試驗測量值由3440g逐漸減小到2830g，加速度變化相對較慢。且同一彈力繩剛度下，跌落高度越大，放大臺加速度也越高。因此，在沖擊放大器的設計中，可選取較小的彈力繩剛度及較大的跌落高度，以實現更高的沖擊放大效果。

4 結論

為了在傳統跌落沖擊試驗臺上獲得更大的沖擊加速度，提出一種結構簡單、操作方便、成本較低及試驗可重復性高的反彈對撞式沖擊放大器。采用經典碰撞理論與動態接觸理論相結合的方法，引入碰撞恢復系數(考慮能量損失)，推導出放大臺加速度及其放大倍數計算公式，對其工作機理展開研究，主要得出以下結論：

(1)放大臺加速度及其放大倍數與跌落高度h、彈力繩剛度k3、預留間隙d、跌落臺質量m1、放大臺質量m2、波形發生器剛度k1、k2及碰撞恢復系數e1、e2等均有關，它們之間的關系是非線性的。

(2)反彈對撞式沖擊放大器能夠將跌落臺加速度放大13.5 倍，沖擊放大臺上產生的最大加速度高達3780g，理論計算誤差約為7%，滿足誤差要求，驗證了理論模型的有效性和可靠性。因此，該理論模型可用于定量地研究系統參數對沖擊加速度的影響，為反彈對撞式沖擊放大器的設計及優化提供理論支撐，進一步用于指導試驗。

(3)當跌落高度一定時，隨著預留間隙的增大，放大臺加速度呈先增大后減小的趨勢，即存在一個理想預留間隙，使得放大臺加速度達到最大。且同一預留間隙下，放大臺加速度隨跌落高度的增加明顯增大。因此，設計沖擊放大裝置時，在沖擊機跌落高度的允許范圍內，可盡量選取理想預留間隙及較大的跌落高度，以獲得更高的沖擊加速度響應。

(4)當跌落高度一定時，隨著彈力繩剛度增加，放大臺加速度緩慢減小。小剛度彈力繩對放大臺具有一定的沖擊放大效果，但與預留間隙相比，彈力繩剛度對放大臺加速度的影響較小。