基于改進HybridA*的非完整約束機器人路徑規劃算法研究

田雨　林松　房殿軍　江競宇

摘要：為了實現單舵輪AGV在物流場景下的精準自主導航，針對基于HybridA*算法搜索的路徑容易貼近障礙物的缺陷和算法在路徑平滑后可能與障礙物沖突的問題，本文提出一種基于改進HybridA*的非完整約束輪式移動機器人路徑規劃方法。對于路徑搜索部分，將距離場地圖引入啟發式函數，以提高搜索效率，并保持搜索路徑遠離障礙物；對于路徑平滑部分，將優化問題轉化為二次規劃問題，通過邊界約束保證避障效果。在ROS平臺上仿真實驗的結果表明，該路徑規劃方法可有效用于非完整約束系統，為單舵輪AGV自主導航的準確運動奠定了路徑智能規劃的基礎。

關鍵詞：非完整約束機器人；路徑規劃；改進HybridA*；二次規劃

中圖分類號：TP242.2 文獻標志碼：A doi：10.3969/j.issn.1006-0316.2023.03.010

文章編號：1006-0316 （2023） 03-0063-09

Path Planning of Robot with Nonholonomic Constraint based on Improved Hybrid A* algorithm

TIAN Yu1，LIN Song1，FANG Dianjun1，2，JIANG Jingyu1

（ 1.School of Mechanical Engineering， Tongji University， Shanghai 201804， China;

2.Qingdao Sino-German Institute of Intelligent Technologies， Qingdao， 266000， China ）

Abstract：In order to achieve precise autonomous driving of the single steering wheel automated guided vehicle （AGV） in logistics scene， this paper proposes a path planning method for wheeled mobile robots （WMRs） with nonholonomic constraint based on improved Hybrid A* algorithm， so that the problems of original Hybrid A* algorithm on obstacles avoidance could be solved. For the path-search part， a distance field is introduced into the heuristic function， which could improve the searching efficiency and keep the search path away from obstacles. For the path-smoothing part， a quadratic programming problem is described to guarantee the obstacle avoidance through boundary constraints. The results of simulated experiments on ROS show that the method proposed could be effectively applied to nonholonomic constrained robots， and could lay the foundation for the accurate movement of single steering wheel AGV on autonomous navigation.

Key words：robot with nonholonomic constraint；path planning；Hybrid A* algorithm；quadratic programming

AGV（Automated Guided Vehicle，自動引導車）作為一種無人操作的智能化搬運設備，在制造業生產、倉儲物流等作業環節中發揮著重要作用。其中，單舵輪AGV具有底盤結構簡單、驅動方式簡明、成本低廉等優點，在工業物流領域被大量應用，但對該類型的AGV進行路徑規劃及其運動控制時，需要額外考慮車輪的非完整約束條件，讓機器人在給定運動路徑下始終保持車輪無滑動滾動的狀態[1]，才能使其在自主導航時保證較高的可控運動精度。如果能為單舵輪AGV自主導航規劃出合理、可達、無碰撞的全局路徑，就可降低軌跡跟蹤控制的難度，顯著提高AGV的運行效率和軌跡跟蹤精度，以此為AGV自主導航的準確運動提供技術支撐。

由國內外相關研究可知，考慮非完整約束系統的路徑規劃方法主要包括曲線插值方法、采樣方法、最優控制方法和機器學習方法[2]。其中，曲線插值和采樣方法由于具備較高的求解速度，是目前實際運用最為廣泛的方法，也更符合AGV的低算力特點和高實時性要求，因此是本文的主要研究方向。Dolgov等[3]提出的HybridA*算法，便是此類考慮非完整約束的早期典型算法，該算法由A*算法改進而來，通過輪式底盤可實現的曲線軌跡來進行節點拓展，滿足輪式車輛的非完整約束。隨后，部分學者以該方法為基礎算法，從不同角度提出了改進方法。任秉韜等[4]設計了可變半徑的RS（Reeds- Shepp）曲線，增加了搜索靈活性；Saeid等[5]引入可見性圖來引導節點擴展，大大降低了擴展節點的數量；還有其他文獻[6-8]在HybridA*基礎上提出不同的子節點拓展方式、啟發函數或節點搜索策略，以提高搜索效率。

另一方面，通過原始HybridA*算法搜索出的路徑存在包含不必要的轉彎和曲率不連續的問題，這在實用中還有待進一步平滑優化。Dolgov[3]采用梯度下降法對HybridA*算法搜索出的路徑進行平滑，此后也有文獻[7-9]采用了基于梯度下降的數值優化方法來對圖搜索出的路徑進行平滑后處理。然而，采用梯度下降法優化得到的路徑無法保證無碰撞，需要反復修改優化目標，直到通過碰撞檢測[7]。此外，HybridA*算法還存在初始搜索的路徑太過貼近障礙物的現象，這不僅不利于AGV的行駛，也會壓縮路徑平滑優化的空間，增加路徑平滑的優化難度。

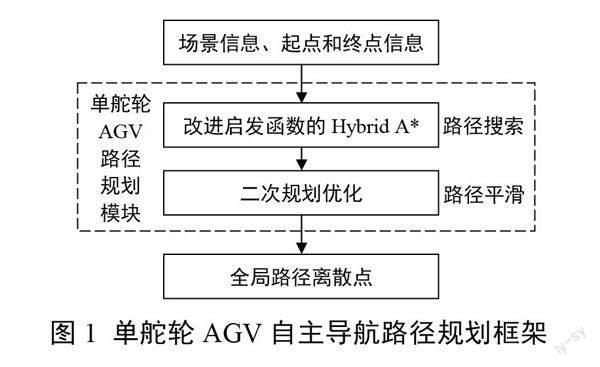
針對以上問題，本文在HybridA*算法的路徑搜索過程中引入距離場，通過動態調整距離閾值和修改啟發式函數的形式，使得初始搜索路徑遠離障礙物；在平滑后處理中，將優化問題描述為二次規劃問題，以線性約束的形式保證優化后路徑的無碰撞性，最終得到適合單舵輪AGV的自主導航路徑規劃方法。其規劃框架如圖1所示。

1 路徑搜索

1.1? HybridA*算法原理

傳統A*算法是一種基于柵格化地圖的圖搜索算法，它的目標是搜索出一條與障礙物無碰撞的距離最短路徑。在柵格地圖中，算法從起點出發，并以此為初始節點，不斷擴展節點周圍的子節點，并且選擇代價函數總值最小的子節點作為下一個搜索點，不斷往復，直至到達終點。公式為：

f（n）＝g（n）＋h（n）? ? ? ? ? ? ? ? ? ?（1）

式中：g（n）為累計代價函數，物理意義是從起始節點到當前節點的累計距離；h（n）為啟發式函數，物理意義是當前節點到目標節點的預估距；f（n）為代價函數，代表在途經當前節點這一條件

下的路徑預估總距離。

核心原理為：

（1）不斷尋找f（n）值最小的無碰撞節點進行擴展。如圖2（a）所示，在初始節點0的周圍，優先擴展無碰撞節點1；

（2）如新節點已經被擴展過，則通過比較g（n）的方式選擇更優路徑。如圖2（b）所示，雖然2節點的f（n）值小于3節點，會被優先擴展，但0－1－3路徑得到的g（n）值小于0－1－2－3的路徑，因此，當3節點擴展后，2節點會被廢棄。

采用這樣的思路，可以將搜索方向引導向預估總路徑最短的方向，而并非沒有目標的依次遍歷，因此可以高效率搜索到總距離最短的無碰撞路徑。

不難看出，A*算法最初的目標是路徑長度最短，因而代價函數主要考慮距離因素；如果在代價函數引入其他因素，則可以得到滿足實際需求的路徑，如時間最優、能量最優等。

HybridA*與A*的算法基本思路相似，區別點主要是拓展節點的方式和代價函數的組成。

在拓展節點部分，A*算法可以向臨近柵格直接擴展，如圖3（a）所示；HybridA*算法則考慮了車輛的非完整約束，子節點位置為車輛以R的轉彎半徑行進l的距離后所在的位置，如圖3（b）所示。

在啟發式函數部分，HybridA*算法對同一個節點用兩種不同的方式計算，取兩種計算方式結果的較大值作為啟發代價。

第一種計算方式考慮非完整約束但忽略障礙物，計算當前節點與目標節點間符合運動學約束的最短路徑，在車輛允許倒車時，一般通過計算RS曲線得到。RS曲線是在無障礙物情況下滿足車輛運動學約束（起點位姿、終點位姿、最小轉彎半徑、允許倒車）的距離最優曲線，如圖4所示。

第二種計算方式為考慮障礙物但忽略非完整約束，計算當前節點與目標節點間的無碰撞最短路徑，一般通過A*等圖搜索算法計算得到。第二種計算方式在障礙物較稠密的區域能夠產生更良好的效果[3]。

此外，HybridA*算法還會在每拓展n個節點時計算該節點到目標位姿的RS曲線，如果曲線與環境障礙物無碰撞，則直接采納該路徑作為剩余路徑，結束搜索過程。這可以減少拓展的節點數量，大大提升搜索效率。完整的Hybrid A*算法流程如圖5所示。

1.2 啟發式函數改進

為使搜索出的路徑遠離障礙物，引入距離場地圖[10]思想，其原理是將柵格地圖基于廣度優先搜索的思想進行遍歷，得到每個柵格點和最近障礙物的距離，被障礙物占據的柵格數值為1，距離障礙物越遠則數值越高。原始柵格地圖和由此生成的距離場地圖對比如圖6所示。

本文所涉及的物流場景一般不具備開闊空間，在該種環境下只考慮障礙物但忽略非完整約束的啟發函數往往效果更優，因此本文舍棄了計算RS曲線作為啟發式函數的部分，而是只對障礙物進行考慮。引入了距離場系數后的啟發式函數可表示為：

式中：Xi為A*算法搜索得到的從當前節點n到目標節點所途徑的總共k個節點中的第i個節點； 為與該節點對應的障礙物距離代價函數； 為該節點對應的距離場數值；K為大于1的安全距離閾值。

式（3）可理解為，節點與障礙物的距離小于閾值時，賦較大的代價值；節點與障礙物的距離大于閾值時，代價值隨距離的增大而減小。

為了驗證啟發式函數的改進效果，本文在ROS Rviz平臺上建立仿真障礙地圖，分別以路徑搜索中較常見三種情況（S型連續彎、U型彎、長直線避障）設定初始位姿和目標位姿進行路徑搜索實驗，如圖7所示。其中，完整障礙地圖尺寸為30 m×20 m，搜索分辨率0.1 m，因而搜索柵格尺寸為300×200；三次實驗的始末位姿已在圖中標出。可以看出，改進后的路徑能夠相較原路徑離障礙物更遠。

在此基礎上，為定量分析改進算法的性能，本文在該地圖上隨機設定起始位姿和目標位姿進行50次重復實驗，箱型圖結果如圖8所示。箱型圖是一種體現數據分布情況的統計圖，其中箱體部分的紅線代表數據中位數（Q2）位置，箱體實線上界與下界分別代表數據上四分位數（Q3）和下四分位數（Q1）；箱體外部的藍色圓圈代表大于Q3－1.5×（Q3－Q1）或小于Q1－1.5×（Q3－Q1）的值，被稱作離群值；箱體虛線上界和下界分別為未離群的最大值和最小值。

圖8中表征兩種算法結果區別的規劃路徑相對長度差為：

式中： 為兩種算法規劃路徑的長度差； 為原算法規劃出的路徑長度； 為改進算法規劃出的路徑長度。

由圖8可以看出，相較于原始HybridA*算法，改進算法在搜索路徑時拓展節點的個數更少、算法總用時更短，在考慮了距離場地圖生成的額外開銷下，總體計算效率仍更優。需要注意的是，為保證顯示尺度，圖8（a）（b）中出現的離群值僅用虛線代替，未標注正確位置，但離群數據中改進算法的結果仍相較原算法效率更高。此外，改進算法搜索的路徑長度在大多數情況下會略大于原始算法的搜索結果，這是考慮了安全避障、放棄距離最優的合理結果，與預期相符。

2 路徑平滑

上述路徑搜索算法能夠粗略得到一條符合非完整約束的可達路徑，但存在不必要的拐彎、路徑曲率變化不夠連續等問題。本文將其描述為標準二次規劃問題，借以來對路徑作進一步平滑處理：以軌跡的距離代價和曲率代價作為優化目標，把原始離散點與障礙物的距離引入約束條件，以保證優化后的軌跡不會與障礙物發生碰撞，最后進行優化求解。

二次規劃問題是一種特殊的非線性規劃問題，其數學模型可表示為：

式中：X為由所要優化的變量構成的矩陣；Q為二次型代價構成的矩陣；c為線性代價構成的矩陣；D為X的可行域。

考慮到由線性約束構成的可行域一定是凸集；而當Q矩陣為半正定矩陣時，目標函數為凸函數。同時滿足上述兩個條件時，該問題為凸二次規劃問題，問題的局部最優解即為全局最優解，因此可以較方便地通過數值方法求得最優解。

2.1 約束條件

二次規劃的目標是對路徑搜索得到的路徑離散點進行進一步優化，對于每一個離散點Pi，用三個變量{xi， yi， di}進行描述，因此對于初始搜索路徑上的n個離散點，應共有3n個變量。如圖9所示。

di為優化后的位置相對原始位置在路徑法線方向上的偏移距離；（xi0， yi0）為離散點原始坐標； 為離散點的朝向，即笛卡爾坐標系中該離散點指向下一離散點的射線與x軸的夾角。

有位置約束：

式中：（ ，? ）為離散點Pi優化后的坐標。

為保證偏移后的離散點不會與障礙物發生碰撞，對偏移量 增加線性約束，其中 的約束上下界 和 根據與障礙物的實際距離計算得到，如圖10所示，滿足：

2.2 優化目標

對離散軌跡點的優化目標有兩個，一是使其減少不必要的拐彎，二是保證路徑的平滑性，避免曲率突變。因此代價函數應包含兩部分，即距離代價和離散曲率代價，分別對應兩個優化目標。

對于第一目標，一般來說，離散點間距之和越小，說明路徑軌跡越直，拐彎越少，同時路徑總長度越短，因此描述為距離代價，建立函數為：

式中： 為距離代價函數； 為距離代價權重； 為離散點間距。

對于第二目標，主要考慮軌跡離散點的離散曲率和曲率的變化率，其中，離散曲率之和越小，說明路徑的平均離散曲率越小；離散曲率的變化率之和越小，說明曲率越連續，兩者都會對路徑的平滑性產生影響。

首先考慮離散曲率的計算方式。如圖11所示，對于在圓弧上的三個離散點，假設離散點間距s近似相等，構造Pi+1相對PiPi+2對稱的輔助點P'i+1，則可由△Pi+1OPi+2和△P'i+1Pi+2Pi+1的相似關系推導得到：

式中： 為Pi處的離散曲率。

在優化函數中為了保持二次形式，將其簡化，得到：

式中： 為離散曲率代價函數； 為離散點處的曲率： 為曲率的變化率； 和 分別為曲率和曲率變化率對應的權重系數。

綜合式（9）和式（13），得到：

式中： 為優化問題的代價函數。

綜上，便將路徑平滑問題描述成一個標準的二次規劃問題，本文將約束條件和優化目標以稀疏矩陣的形式表達，采用OSQP開源求解器進行求解。

2.3 平滑效果

本文針對圖7（b）II所示的初步搜索路徑，采用不同的權重系數進行路徑平滑，對應的路徑離散曲率折線圖如圖12所示，平滑效果如圖13所示。

從圖12可以看出，初始搜索路徑中包含大量折線尖點，說明初始路徑的離散曲率突變劇烈；而二次規劃優化后的路徑有效改善了初始搜索路徑的形狀，減少了不必要的拐彎，并盡可能拉直，大大降低了路徑的離散曲率。

此外，對比三種不同權重的二次規劃優化結果也可以看出，權重系數的取值會影響路徑的特性。利用這一優化算法，本文在該地圖上隨機設定起始位姿和目標位姿，選用不同的平滑權重系數進行50次重復實驗。

系數選取如表1所示，箱型圖結果如圖14所示。

圖14（a）（b）中，分布越靠下方，說明路徑越平滑；圖14（c）為平滑后路徑與初始搜索路徑的長度差，距離差在大于0的前提下越大，說明平滑后路徑的距離越短，“拉直”效果越好，其表達方式為：

式中： 為平滑后路徑與初始搜索路徑的長度差； 為初始路徑長度（對照組）； 為平滑路徑長度。

通過對比s1、s2兩組權重的實驗結果可以看出，Wsmo2的增大可以使路徑更平滑；結合圖13的實驗結果分析，Wsmo2的增大還可以使曲率的變化更加連續。而s3/s4與s1/s2相比的區別在于引入了Wdis，從圖14可以看出，Wdis的引入會縮短路徑的長度，對路徑的“拉直”效果更好，但隨著Wdis的增加，路徑曲率最大值會明顯增大，這會導致局部曲率偏大。

考慮上述三個系數對路徑形狀的影響后，本文在該尺度地圖上最終選擇的權重系數比值為Wdis：Wsmo1：Wsmo2＝0.04：1：10，選取不同目標點進行全局路徑規劃實驗，最終效果如圖15所示。可以看出，本文所提出的基于改進HybridA*的非完整約束機器人路徑規劃方法在各種障礙場景中均能規劃出平滑且無碰撞的全局路徑。

3 結論

本文針對傳統HybridA*算法在應用于非完整約束機器人全局路徑規劃時路徑容易貼近障礙物的缺陷，和算法在路徑平滑后可能與障礙物沖突的問題，將全局路徑規劃分為路徑搜索和路徑平滑兩部分進行算法改進。

其中，在路徑搜索部分，采用HybridA*圖搜索方法，在搜索的啟發式函數部分引入距離場地圖，使搜索路徑遠離障礙物并提高搜索效率；在路徑平滑部分，將平滑問題構建成二次規劃問題進行求解，通過約束優化后路徑離散點的極限位置以保證路徑的無碰撞性，并基于向前差分的思想引入表征曲率變化率的優化代價，進一步提升路徑的平滑程度。

在基于ROS平臺的仿真實驗結果表明，本文提出的全局路徑規劃算法可有效應用于非完整約束AGV，能夠同時保證避障和路徑平滑性，并基本滿足系統的實時性要求，為AGV自主導航的精準運動奠定了基礎。

參考文獻：

[1]譚躍剛. 非完整機器人的原理與控制[M]. 北京：科學出版社，2011.

[2]李柏，張友民，邵之江. 自動駕駛車輛運動規劃方法綜述[J]. 控制與信息技術，2018（6）：1-6.

[3]Dolgov D，Thrun S，Montemerlo M，et al. Path Planning for Autonomous Vehicles in Unknown Semi-structuredEnvironments[J]. The International Journal of Robotics Research，2010，29（5）：485-501.

[4]任秉韜，王淅淅，鄧偉文，等. 基于混合A～*和可變半徑RS曲線的自動泊車路徑優化方法[J]. 中國公路學報，2022，35（7）：317-327.

[5]Saeid S，Duong-Van N，Klaus-Dieter K. Guided Hybrid A-Star Path Planning Algorithm for ValetParking Applications[C]. Beijing， China：2019 5th International Conference on Control， Automation and Robotics，2019：570-575.

[6]Tu K.，Yang S.，Zhang H.，et al. Hybrid A* Based Motion Planning for Autonomous Vehicles inUnstructured Environment[C]. Sapporo， Japan：2019 IEEE International Symposium on Circuits and Systems，2019：1-4.

[7]陳鑫鵬，徐彪，胡滿江，等. 一種基于等步長分層拓展的混合A～*路徑規劃方法[J]. 控制與信息技術，2021（1）：17-22，29.

[8]齊堯，徐友春，李華，等. 一種基于改進混合A～*的智能車路徑規劃算法[J]. 軍事交通學院學報，2018，20（8）：85-90.

[9]Kurzer K. Path Planning in Unstructured Environments： A Real-time Hybrid A* Implementation for Fast and Deterministic Path Generation for the KTH Research Concept Vehicle[D]. Stockholm：KTH Royal Institute of Technology，2016.

[10]Lau B，Sprunk C，Burgard W. Improved updating of Euclidean distance maps and Voronoi diagrams[C]. IEEE/RSJ International Conference on Intelligent Robots & Systems. IEEE，2010.

收稿日期：2022-12-15

作者簡介：田雨（1997－），男，天津人，碩士，主要研究方向為機械制造及其自動化，E-mail：tianyu9741@163.com。*通訊作者：林松（1957－），男，四川廣元人，工學博士（德），主要研究方向為產品研發方法及其智能設計、虛擬產品生產及其數字孿生、智能裝置及其人機協調、技術系統可靠性及其安全設計，E-mail：slin@tongji.edu.cn。