破除思維定式 明晰概念圖像
2023-08-19 02:14:58林品玲葉誠理
中學數學研究 2023年8期
林品玲 葉誠理

近年來的高考和各地質檢中,經常出現三角函數圖象與性質中求ω的取值范圍問題,通常在選填壓軸題位置出現,學生解題中可能存在一定的困難,按照原有的思維定式造往往成求解范圍的偏差.如何破除解題障礙,本文就這一類問題學生中產生的常見錯誤展開分析,并提煉出相應的解題策略,以饗讀者.
1.錯看函數零點
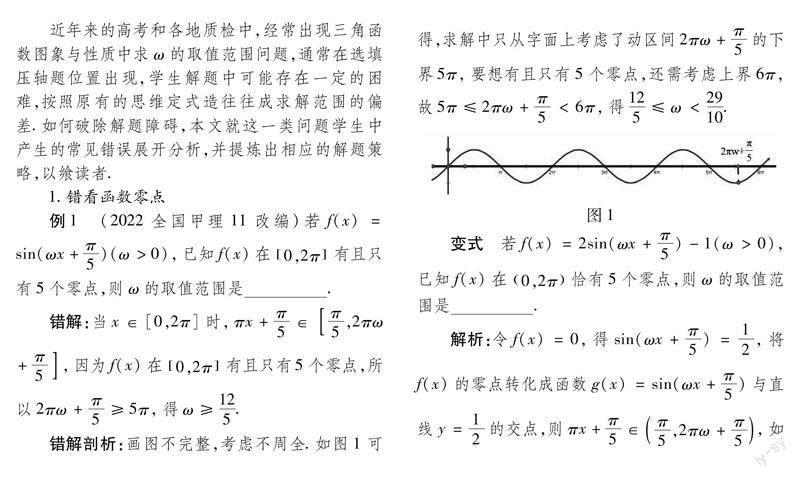
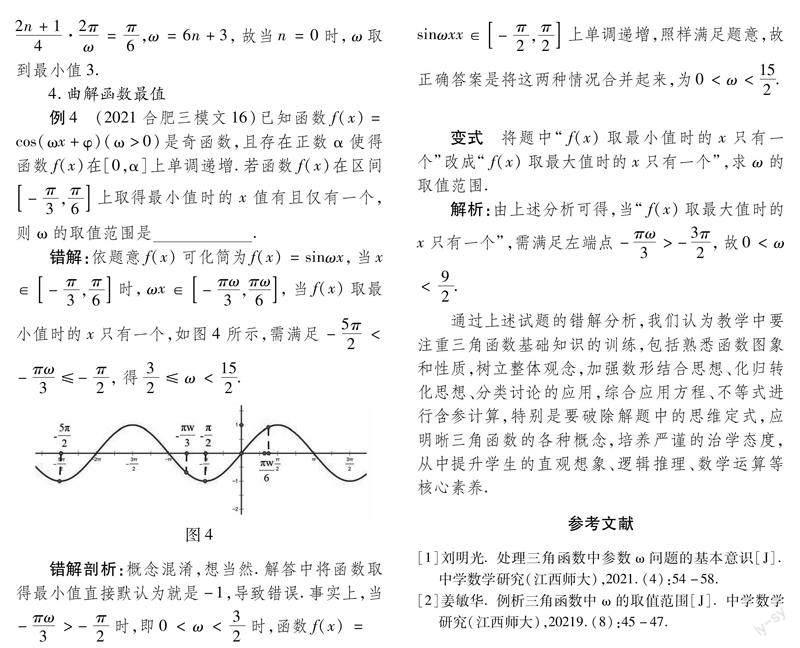
例1 (2022全國甲理11改編)若f(x)=sin(ωx+π/5)(ω>0),已知f(x)在0,2π有且只有5個零點,則ω的取值范圍是 .
錯解:當x∈[0,2π]時,πx+π/5∈π/5,2πω+π/5,因為f(x)在0,2π有且只有5個零點,所以2πω+π/5≥5π,得ω≥12/5.
通過上述試題的錯解分析,我們認為教學中要注重三角函數基礎知識的訓練,包括熟悉函數圖象和性質,樹立整體觀念,加強數形結合思想、化歸轉化思想、分類討論的應用,綜合應用方程、不等式進行含參計算,特別是要破除解題中的思維定式,應明晰三角函數的各種概念,培養嚴謹的治學態度,從中提升學生的直觀想象、邏輯推理、數學運算等核心素養.
參考文獻
[1]劉明光. 處理三角函數中參數ω問題的基本意識[J]. 中學數學研究(江西師大),2021.(4):54-58.
[2]姜敏華. 例析三角函數中ω的取值范圍[J]. 中學數學研究(江西師大),20219.(8):45-47.
猜你喜歡
中學數學雜志(2022年6期)2022-11-18 14:26:15
中學數學雜志(2022年6期)2022-11-17 23:05:58
中學數學雜志(2022年6期)2022-11-14 19:02:07
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學數學雜志(2022年6期)2022-09-05 08:09:54
小哥白尼(野生動物)(2022年6期)2022-08-17 08:05:28
小哥白尼(野生動物)(2022年4期)2022-07-16 03:37:32
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小哥白尼(野生動物)(2022年2期)2022-06-01 06:21:20
小哥白尼(野生動物)(2022年1期)2022-04-26 14:01:18

