基于粒子群優化的噴施無人機PID 控制*
姜舒涵 ,龐 濤 ,張新悅 ,周彥君 ,王萌謀 ,曹湘雨 ,梁靖賢 ,應安青
(四川農業大學機電學院,四川 雅安 625000)
0 引言
中國自古以來便是農業大國,有悠久的農耕歷史。農業灌溉中,藥物噴施始終是重中之重。在如今的噴施作業中,人工作業仍占有很大比重。然而,對于大面積耕地來說,人工噴施效率低下、農藥利用率低、成本高[1]。近年來,隨著綠色農業、精準農業的需求不斷提高,國內農業逐步向機械化、自動化、規模化、多樣化、精細化方向發展,轉向“高產、優質、高效、安全、生態”的發展方式,致力于建設“優質、安全、生態”的現代農業,因此正迫切需要高效率、低污染、自動化機械裝備[2]。目前,高速發展的無人機技術能夠很好地代替大面積的人工噴施,可以提高效率,降低成本[3]。但現如今的噴施無人機在動態復雜環境下,仍存在施藥響應不夠精確快速、穩定性欠佳等問題[4]。
基于以上現狀,本文設計了一種基于粒子群優化的噴施無人機PID 控制方法,能根據具體操作環境,實時調節藥液泵轉速,實現不同環境下施藥量的最優化控制,進而有效減少農藥浪費,提高農藥利用率。在此基礎上,將該系統與傳統PID 控制及GA 算法優化PID 控制系統進行比較,分析三者在噴施系統控制上的性能,以期為構建精度高、穩定性強的無人機噴施系統提供技術支持。
1 被控系統數學模型的建立
獲得準確的數學模型是開展動態環境下噴施無人機藥液泵控制的前提。在無人機噴施系統中,可將藥液泵供藥視為一種時變壓力的穩壓供水系統。穩壓供水系統通過調節變頻器改變水泵的供水量,從而達到穩定水壓的目的,其機理[5]是從恒壓供水演變而來,分為壓力上升階段和恒壓階段。其中,壓力上升階段是一階慣性環節,恒壓階段為純滯后環節。因此,供藥系統模型可表示為[6-8]:
式中,G1——供藥系統傳遞函數;T1——供藥系統的慣性時間常數;k1——供藥系統的增益;τ——供藥系統的時滯常數;s——拉普拉斯變換域中的頻率,是一個復數變量;np——傳遞函數輸入,即供藥系統中離心泵的轉數;p0——傳遞函數輸出,即供藥系統的出口壓力。
變頻器和藥液泵電機可近似為等效時間常數T2的一階慣性環節,可表示為:
式中,G2——調速系統傳遞函數;T2——調速系統的慣性時間常數;k2——調速系統的增益;s——拉普拉斯變換域中的頻率,是一個復數變量;fc——傳遞函數輸入,即供藥系統中變頻器的輸入頻率;nm——傳遞函數輸出,即供藥系統中電機的轉速。
系統中其他控制及檢測環節與供藥系統的時間常數相比可以忽略,可以看作一個比例環節:
式中,G3——其他系統傳遞函數;k3——其他系統增益。
設定噴施系統采用離心泵供給藥液,則該系統中電機的轉速等于離心泵的轉速,因此整個供藥系統的模型可以表示為上述3個環節的串聯模型,即:
式中,G——系統傳遞函數;k——系統的總增益。
在一定范圍降頻、參數變化小等工況中,可以認為系統模型是一階慣性加時滯的模型,但當系統處于升頻或參數變化較大、較快的過程中,系統模型變為二階慣性加時滯模型,其結構較為復雜。本文選擇系統處于升頻狀態,因此系統模型為二階慣性加時滯模型,模型傳遞函數為[7]:
2 基于PSO算法的PID控制系統設計
2.1 PID控制
P I D 控制系統由被控對象和控制器構成[6],PID 控制器由比例單元(Proportional)、積分單元(Integral)和微分單元(Differential)構成。PID 控制器根據設定值r(t)和實際輸出值c(t)偏差,通過比例、積分、微分的運算得到控制量,進而對控制對象進行控制。PID控制系統原理框圖如圖1所示。

圖1 PID 控制系統原理框圖
PID 控制是比例、積分、微分控制規律的線性組合,其輸入輸出關系表示為:
式中,Kp為比例系數;Ti為積分時間常數;Td為微分時間常數;r(t)為被控對象設定值;c(t)為實際值;e(t)為系統誤差;u(t)為控制器的輸出量。
積分系數為:
微分系數為:
通過拉普拉斯變換,可得PID 控制器的傳遞函數為:
式中,U(s)為輸出函數,E(s)為輸入函數。
噴施系統具有非線性、滯后性和時變性的特點,需要實時整定Kp、Ki、Kd三個參數,但傳統的PID 控制參數不可動態調節,且依賴人為經驗。因此,本次研究首先采用GA 算法優化PID 控制,實現對PID 參數的實時更正。
2.2 GA算法優化PID控制
遺傳算法(Genetic Algorithm, GA)是一種自適應全局尋優算法[8]。其基于達爾文生物進化論的自然選擇和遺傳學機理,對自然界中生物的遺傳和進化過程進行計算機模擬,搜索問題的最優解。GA 算法流程圖如圖2所示。
圖2 GA算法流程圖
在噴施系統的GA-PID 控制研究中,以電機轉速的真實值和預設值之差e(t)、響應曲線的超調量pos、上升時間tr和峰值時間ts構建目標函數:
式中,w1、w2、w3、w4為權重。
通過GA 算法的優化程序和參數調整,得到PID參數Kp、Ki、Kd的最優解,相較于傳統的PID 控制,噴施系統的穩定性、快速性和準確性均得到提高。
本次研究不僅設計出GA 算法優化的PID 控制器,還將PID 控制和粒子群優化算法相結合,對PID控制參數進行更精確的調整,以達到精度高、穩定性好的噴施控制效果,進而實現精準噴施。
2.3 基于改進PSO算法的PID控制器設計
2.3.1 粒子群算法
粒子群算法(Particle Swarm Optimization, PSO)為智能優化算法,是通過模擬鳥群覓食行為而發展起來的一種基于群體協作的搜索算法[9]。PSO 能夠解決非線性、不可微和多峰值等復雜系統的優化問題,具有自適應能力強、收斂速度快且易于實現的優點,適用于噴施系統PID 控制器的參數整定。粒子群算法的表示如下,在N維的搜索空間中,總粒子數為n,粒子i的空間位置表示為:
第i個粒子的速度表示為:
將每個粒子的位置代入目標函數,即可計算出適應值fi,根據適應值的大小衡量粒子空間位置Xi的優劣。第i個粒子目前搜索到的最優位置表示為:
粒子群目前搜索到的最優位置表示為:
粒子不斷更新自己的位置和速度,其變化公式如下所示:式中,ω為粒子的慣性權重;c1、c2為學習因子;r1、r2為在區間(0,1)上均勻分布的隨機數;分別為粒子i在t時刻和t+1 時刻的速度,分別為粒子i在t時刻和t+1時刻的位置。
粒子的自我認知部分為:
粒子的社會認知部分為:
粒子的社會認知部分反映粒子和整個粒子群的信息交流[10]。一般情況下,學習因子c1=c2=2,慣性權重ω取0.9。
2.3.2 改進PSO算法優化PID控制
PSO 算法具有計算效率高、算法簡單的優點,但容易陷入局部極值。在PSO 算法中,慣性權重ω體現粒子以前速度對當前速度的影響,較大的慣性權重有利于全局搜索,較小的慣性權重有利于局部搜索。因此,需要調整合適的慣性權重,平衡PSO 算法的全局搜索和局部搜索的能力[11]。本文選用自適應慣性權重的改進方法,對于噴施系統的PID 控制,適應度越小,距離最優解越近,選用局部搜索;適應度越大,距離最優解越遠,選用全局搜索[12-14]。自適應慣性權重的調整公式為:
式中,ωmin和ωmax為預先設定的最小慣性系數和最大慣性系數。
t時刻所有粒子的平均適應度為:
t時刻所有粒子的最小適應度為:
改進PSO 算法可以有效搜索不同區域,得到全局最優解。
噴施系統的PID 控制器由Kp、Ki、Kd三個參數決定,則PID 控制器的參數優化是三維函數的優化問題[15-17]。基于改進PSO 優化算法的PID 控制流程如下:
1)初始化參數,設置粒子數量、變量個數、學習因子、慣性權重、迭代次數等參數;
2)隨機初始化粒子所在的位置和速度;
3)計算出每一個粒子的適應度,本研究選用ITAE指標作為適應度函數,其定義為:
4)更新每個粒子的速度和位置,并進行調整;
5)重新計算粒子的適應度,并進行比較;
6)通過更新粒子的位置和速度,得到全局最優的粒子;
7)若達到迭代次數,則結束循環;若未達到迭代次數,則返回步驟4。
基于改進的PSO 算法可實現PID 控制器的參數優化,適用于噴施系統的PID控制。
3 算例驗證及實例求解
為了驗證控制效果,采用MATLAB 搭建了控制仿真系統。基于PSO 的PID 控制系統設計流程如圖3 所示,該系統下文中采用PSO-PID 表示。根據已構建的噴施水泵數學模型,在Simulink 中搭建PSO-PID仿真模型,如圖4所示。

圖3 基于PSO的PID 控制系統設計流程圖

圖4 Simulink中搭建PSO-PID 仿真模型
分別基于PID、GA-PID、PSO-PID 控制算法,對以上系統進行仿真實驗。首先,設定水泵電機轉速目標量為500 rad/s,PSO 算法的參數選擇如下:種群規模為100;最大迭代次數為50 次;最小適應值為0.01;慣性權重最大值為0.9,慣性權重最小值為0.1;學習因子為0.2;維數為3,得到PSO 最優個體適應值曲線和Kp、Ki、Kd優化曲線,如圖5、圖6 所示。為了驗證該參數的普遍性,在不改變控制參數的前提下,設定目標量為1 400 rad/s 與2 500 rad/s 再次實驗,分別得到目標量為500 rad/s、1 400 rad/s、2 500 rad/s的控制曲線對比圖,分別如圖7、圖8、圖9 所示。

圖5 最優個體適應值

圖6 Kp、Ki、Kd優化曲線

圖7 目標量為500 rad/s的控制曲線對比圖

圖8 目標量為1 400 rad/s的控制曲線對比圖
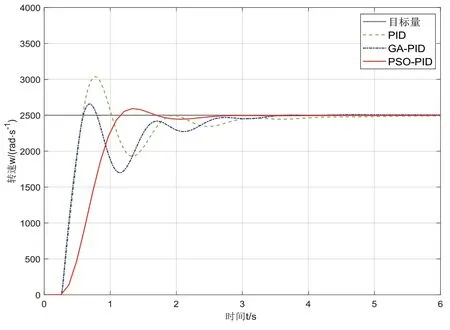
圖9 目標量為2 500 rad/s的控制曲線對比圖
由圖5 可知,目標量為500 rad/s 時,在第46 次迭代找出了該適應度函數的最優適應度,值為158.970 4。由圖6可知,最佳個體Kp值為0.206 8;Ki值為0.155 98;Kd值為0.044 685。為消除隨機因素的影響,根據目標量為500 rad/s 時的參數,設定目標量為1 400 rad/s 與2 500 rad/s 再次實驗。由圖7~9 可知,PID的調節時間長且超調量大,GA-PID 的調節時間較長且超調量較大,PSO-PID 的性能均優于PID 和GA-PID 控制。
表1 展示了3 次控制實驗中,不同目標量控制算法的平均性能指標對比。由此可見,PID 的平均調節時間為2.688 s,GA-PID 的平均調節時間為2.396 s,PSO-PID 的平均調節時間為1.037 s;PID 的平均超調量為21.52%,GA-PID 的平均超調量為6.25%,PSOPID的平均超調量為2.83%。

表1 三個不同目標量控制算法性能比較
綜上所述,PSO-PID 的平均調節時間更短,達到穩態值更快,且超調量更小,穩定性更強,因此噴施水泵供水控制系統基于粒子群優化的PID 控制效果最優,可應用于噴施無人機控制系統。
4 結論
1)課題組提出了一種基于PSO 的噴施無人機控制方法,能夠實現動態環境下的噴施無人機控制。
2)MATLAB 仿真表明,基于PSO 算法優化的PID 控制在水泵供水控制中的平均調節時間最短、達到穩態值最快、超調量最小且穩定性相對最強,通過PSO-PID 可以實現無人機智能噴施系統中的最優控制效果。
3)通過構建PSO 噴施水泵數學模型,基于PSO算法優化的PID 控制穩定性及動態性能較好,可以很好地克服傳統PID 以及GA-PID 算法出現的穩定性以及穩定性較差的問題,可有效提高實際噴施過程中的噴施效率。

