基于Kriging代理模型的環形網狀天線展開過程規劃

楊癸庚，衛鑫鵬，2，樊 浩，湯奧斐，孔令飛，李鵬陽

(1. 西安理工大學機械與精密儀器工程學院，西安 710048；2. 中國電子科技集團公司第三十九研究所，西安 710065)

0 引 言

環形網狀天線具備口徑大、收納率高、面密度小等優點,是目前大型可展開天線的理想結構形式,已被應用于電子偵察、空間通信、導航等領域[1-4]。由于受到航天運載工具限制,在衛星發射階段,天線處于收攏狀態并固定在火箭整流罩內,當衛星進入預定軌道后,天線展開至工作狀態。環形網狀天線的展開過程是一個受鉸鏈摩擦、鉸鏈間隙、索網張力、驅動索柔性等多種因素影響的非線性時變過程[5-6],天線能否在軌順利展開決定著航天器任務的成敗。因此,對環形網狀天線的展開過程進行合理規劃,是保證其正常工作的重要前提。

在環形網狀天線展開過程規劃方面,李團結等[7]提出了“勻加速-勻速-勻減速”的展開過程規劃,該方法存在展開角加速度不連續問題,導致天線受到較大的沖擊。Li[8]進一步提出了基于五次多項式的展開過程規劃,該方法可以在一定程度上減小加速度沖擊。為了進一步減小沖擊,張逸群等[9-10]采用Bezier函數描述驅動繩索的收納過程,通過優化設計驅動繩索的收納過程實現天線展開角加速度峰值最小。然而,上述方法均基于運動學分析對天線進行展開過程規劃,當考慮天線實際展開過程會受到鉸鏈摩擦、索網張力、驅動索柔性等多種非線性因素的影響時,基于運動學的規劃在天線的實際展開動力學響應中仍然可能存在較大的沖擊[11-12]。因此,有必要進行基于動力學分析的天線展開過程規劃。

高精度動力學分析模型是進行基于動力學分析的天線展開過程規劃的前提。在環形網狀天線動力學建模與分析方面,Li等[13]基于多體系統動力學的Lagrange方法,將內部索網張力等效為彈簧力,建立了環形網狀天線的展開過程動力學模型,該方法將索網張力等效為線性彈簧力,導致建模精度不足。文獻[14-15]從能量角度出發,分別針對圓環形和橢圓環形網狀天線,推導了天線展開過程中索網彈性勢能與展開角之間的非線性關系,該方法能夠合理分析張緊索網對桁架鉸鏈的作用力,但是難以描述展開初期索網的松弛狀態。為此,Zhang等[16-17]采用彈性懸鏈線單元實現了索網結構松弛-張緊狀態的統一描述,研究了展開過程中桁架鉸鏈受到的索網張力變化規律,并通過實驗驗證了索網張力分析方法的正確性。此外,文獻[11]建立了考慮鉸鏈摩擦、索網張力及驅動繩索柔性的環形網狀天線展開動力學模型,實現了綜合考慮多種非線性因素的展開過程動力學分析。總之,隨著動力學模型中考慮的因素越來越全面,建模精度越來越高,計算也會越來越耗時。若采用高精度動力學模型進行天線展開過程規劃,雖然能夠滿足精度要求,但勢必會導致總體優化過程因計算成本高而難以實現。因此,如何在保證計算精度的條件下提高優化效率是實現基于動力學分析的環形網狀天線展開過程規劃的關鍵。

代理模型技術是解決高精度分析模型計算耗時問題的有效途徑[18-24]。目前常用的代理模型包括響應面模型[18]、徑向基模型[19-20]、Kriging模型[21-24]等。各種代理模型中,Kriging模型適用于解決計算耗時大的黑箱問題,已在多個領域廣泛應用。因此,本文將基于Kriging模型開展環形網狀天線的展開過程動力學分析及展開過程規劃研究。

本文基于Kriging模型建立環形網狀天線展開過程動力學分析的代理模型,基于動力學代理模型提出非自適應和自適應兩種優化策略對天線的展開過程進行最優規劃,并通過案例分析研究不同優化策略的優化效果和計算效率。

1 環形網狀天線展開過程規劃問題

1.1 展開過程動力學模型

環形網狀天線結構主要由環形桁架、索網結構和驅動繩索系統組成,索網結構在預張力的作用下張拉成形,環形桁架為索網結構提供邊界支撐,如圖1所示。

圖1 環形網狀天線整體模型

環形桁架由一系列基本的平行四邊形單元組成,每個平行四邊形單元由兩個橫桿、兩個豎桿、1個粗斜桿和1個細斜桿組成,如圖2所示。驅動繩索通過導向滑輪和空心斜桿貫穿于整個環形桁架中。驅動電機通過收納驅動繩索改變四邊形單元對角線長度,從而實現環形桁架的展開。

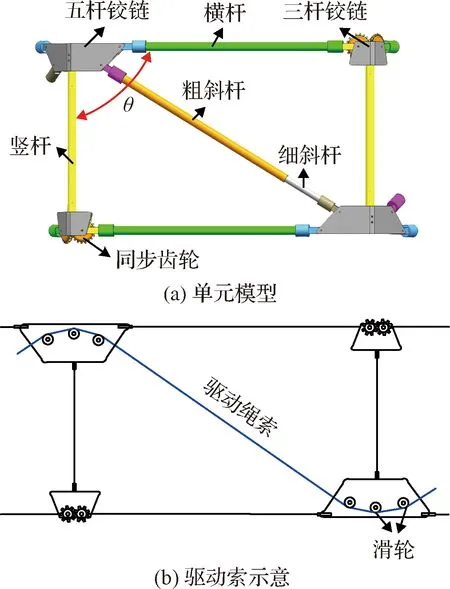
圖2 平行四邊形單元

天線展開過程中,環形桁架的桿件和鉸鏈的彈性變形較小,可視為剛體單元[15]。與環形桁架相比,驅動繩索的柔性較大,將驅動繩索離散為多個小圓柱體單元,小圓柱體單元之間采用Bushing力連接,Bushing力的計算公式如下

(1)

驅動索在運動過程中需要經過導向滑輪以確保在整個展開過程中驅動索與斜桿不發生干涉,驅動索與滑輪之間的相互作用采用接觸力進行約束。展開過程中滑輪的彈性變形可以忽略不計,也視為剛體單元。

綜上,基于拉格朗日乘子法建立同時考慮鉸鏈摩擦、驅動繩索柔性和索網張力的天線系統展開過程動力學模型如下

(2)

式中:q為系統的廣義坐標;M,C,K分別為系統的質量陣、阻尼陣和剛度陣;λ為拉格朗日乘子;Φ(q)為系統的約束條件;Φq為約束條件的雅克比矩陣;Q為系統受到的廣義力。廣義力Q可表示為

Q=Ff(t)+Fc(t)

(3)

式中:Ff(t)為系統受到的摩擦力,其大小由各個鉸鏈處的摩擦系數決定;Fc(t)為張拉索網結構作用在桁架鉸鏈上的時變外載荷,Fc(t)可通過文獻[16]中的松弛索網找形方法確定。

1.2 展開過程規劃問題

天線展開過程中,電機通過收納驅動繩索改變平行四邊形單元的對角線長度,從而驅動整個環形桁架實現展開。根據文獻[10],驅動索長度的收納過程可采用Bezier函數描述,通過合理設計Bezier函數的控制點參數可以獲取天線的最優展開軌跡。

為減少天線在展開過程中受到的沖擊力并降低驅動能耗、減少系統驅動成本,本文將展開角加速度峰值和驅動功率峰值最小化作為設計目標,建立基于動力學分析的天線展開過程規劃優化模型(P-I)如下

(4)

需指出,yθ(x)和yp(x)需要基于式(2)對環形網狀天線進行展開過程動力學分析得到。由于環形網狀天線的動力學模型中包含了鉸鏈摩擦、索網張力、驅動索柔性等多種非線性因素,其動力學響應的求解過程耗時非常大,而優化模型(P-I)的尋優過程又需要對動力學模型進行多次調用,這將導致優化過程難以實現。為此,本文基于動力學代理模型對環形網狀天線的展開過程進行最優規劃。

2 基于Kriging代理模型的展開過程規劃

2.1 Kriging代理模型

Kriging模型對于非線性程度較高的分析設計問題具有較好的擬合精度,可表示為[23]

(5)

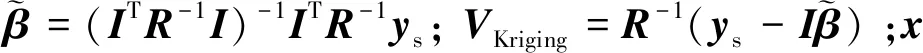
根據優化模型(P-I),環形網狀天線的展開過程動力學分析的輸入設計變量為描述驅動索收納過程的Bezier函數的控制點參數x,輸出目標函數為展開角加速度峰值yθ(x)和驅動功率峰值yp(x)。因此,基于Kriging模型構建環形網狀天線展開過程動力學代理模型的流程如下:

1) 確定設計變量樣本集。采用拉丁超立方試驗設計方法[24]獲得天線展開過程的控制點參數樣本矩陣X。

2) 確定響應樣本集。調用展開過程動力學模型,獲取設計變量樣本集X對應的展開角加速度峰值和驅動功率峰值的響應值,響應樣本集可表示為

Y=[yθ,yp]

(6)

式中:yθ為展開角加速度峰值響應樣本集;yp為驅動功率峰值響應樣本集。

3) 確定樣本集。用于構造Kriging代理模型的樣本集為S=[X,Y]。

4) 構建代理模型。基于樣本集S,根據式(5)構建環形網狀天線展開過程動力學分析的代理模型,可表示為

(7)

2.2 優化策略

根據樣本點的獲取方式不同,可將天線展開過程規劃的優化策略分為非自適應策略和自適應策略兩種類型。

2.2.1非自適應策略

基于非自適應策略的天線展開過程最優規劃流程如圖3所示。具體實現過程如下:

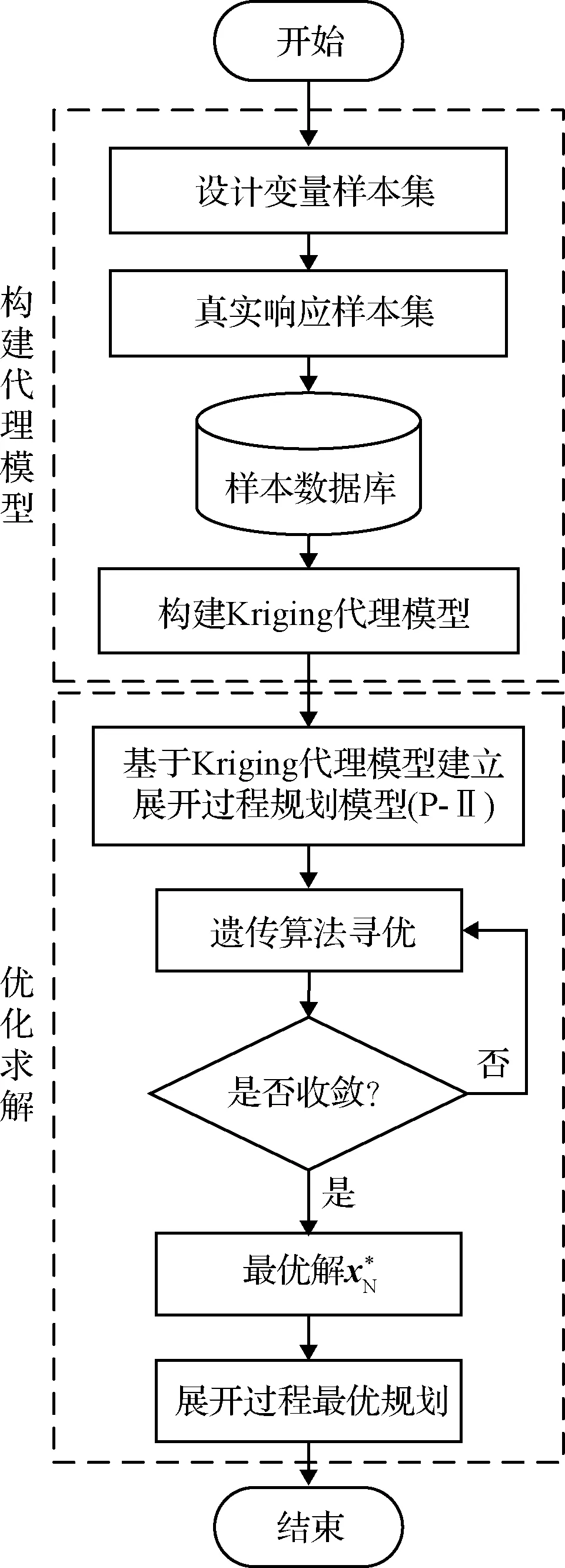
圖3 基于非自適應策略的展開過程規劃流程

1) 采用第2.1節的方法,基于Kriging模型構建環形網狀天線展開過程動力學分析的代理模型。

2) 將優化模型(P-I)中的隱式目標函數更新為Kriging代理模型,則優化模型(P-I)可轉化為模型(P-II)

(8)

3) 采用遺傳算法對優化模型(P-II)進行全局尋優,直到滿足收斂條件為止。

5) 輸出天線展開過程最優規劃結果。

基于非自適應策略的天線展開過程規劃方法中,需要一次性采集足夠多的初始采樣點,才能保證Kriging代理模型的擬合精度,進而確保優化結果的有效性。

2.2.2自適應策略

為了在滿足精度的條件下,減少樣本點數目,進一步提高優化效率,提出基于序列采樣方式的自適應優化策略。基于自適應策略的天線展開過程最優規劃流程如圖4所示。具體實現過程如下:

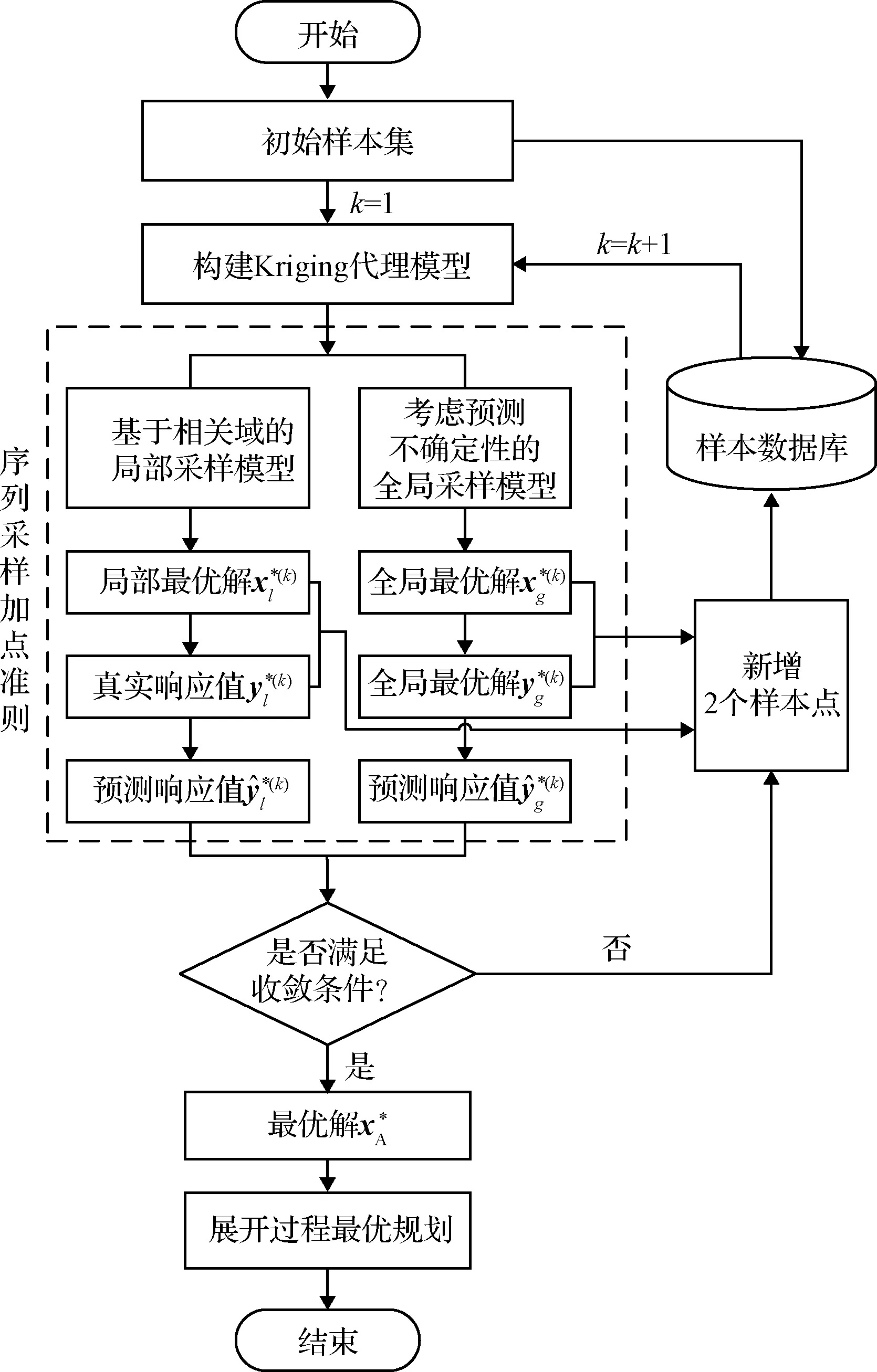
圖4 基于自適應策略的展開過程規劃流程

1) 確定初始樣本集。采用拉丁超立方試驗設計方法獲取N0個初始樣本點,并保存到樣本數據庫。初始樣本點數量N0取為

(9)

2) 基于當前的樣本數據庫,采用第2.1節的方法,基于Kriging模型構建環形網狀天線展開過程動力學分析的代理模型。

3) 構建序列采樣的加點準則。采用平衡局部與全局尋優的方法,分別建立局部采樣模型和全局采樣模型,獲取2個新增采樣點。

(1) 對于第k個迭代步,建立基于相關域的局部采樣模型(P-III)如下:

(10)

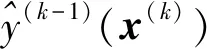
(11)

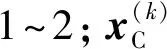
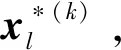
(12)

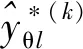
(2) 對于第k個迭代步,綜合考慮Kriging模型的預測方差和設計點與已有樣本點之間最小距離來構建全局采樣模型,全局加點準則函數可表示為

|i=1,2,…,ns}

(13)

基于此,建立考慮預測不確定性的全局采樣模型(P-IV)如下

(14)

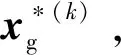
(15)

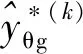
4) 判斷當前迭代步的局部采樣點是否滿足收斂條件。若滿足收斂條件,則執行步驟5);若不滿足,則令k=k+1,并重復步驟2)～步驟4),直到滿足收斂條件為止。為了保證目標函數迭代收斂且在最優解附近代理模型精度足夠高,收斂條件為

(16)

式中:上標(k-1)和(k)分別表示第(k-1)次迭代和第k次迭代的結果,ε1,ε2,ε3,ε4為收斂精度。

6) 輸出天線展開過程最優規劃結果。

3 算例分析

3.1 模型參數

本文對圖1所示的環形網狀天線進行展開過程動力學建模與展開過程規劃,該天線由6個平行四邊形單元組成,天線展開態口徑為1 m、高度為0.3 m、前后網面焦距為0.45 m。該天線模型中,桿件的材料為碳纖維,其彈性模量為150 GPa,密度為1.8×103kg/m3;鉸鏈、同步齒輪和滑輪的材料為鋁合金,其彈性模量為72 GPa,密度為2.7×103kg/m3;索網材料為芳綸纖維,其彈性模量為20 GPa,密度為1.685×103kg/m3;驅動繩索為鋼絲繩,其彈性模量為150 GPa,密度為7.85×103kg/m3。

基于第1.1節的動力學模型,采用ADAMS軟件建立環形網狀天線的展開過程動力學仿真模型。仿真模型中,以圖1所示的一個豎桿為固定端,設定各個鉸鏈之間的摩擦系數為0.1,驅動索與滑輪之間的摩擦系數為0.01。

本例中,天線的展開周期為tp=10 s[25],選用10階Bezier函數描述驅動索收納長度的變化規律。根據角速度和角加速度的連續性條件[10],10階Bezier函數所需要的控制點參數變量數目為5個。基于此,一旦給定一組控制點參數,即可通過調用動力學仿真模型得到天線展開過程的展開角加速度時程數據和驅動功率時程數據,進而可提取出整個展開過程中的展開角加速度峰值和驅動功率峰值。在電腦配置為CPU 3.70 GHz、內存16 G的條件下,單次調用動力學分析模型的計算耗時約為17 min。若直接采用優化模型(P-I)進行環形網狀天線展開規劃,尋優過程需要大量的搜索才能找到全局最優解,往往需要成千上萬次調用動力學分析模型,總體優化過程的計算成本會非常高甚至難以實現[20]。因此,有必要采用基于代理模型的優化策略進行環形網狀天線的展開過程規劃。

3.2 基于非自適應策略的展開過程規劃

采用第2.2.1節的非自適應策略對天線的展開過程進行最優規劃。

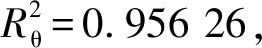
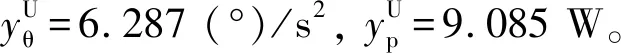
非自適應策略的優化結果如表1所示,與文獻[10]相比,本文方法得到的天線展開角加速度峰值及驅動功率峰值分別下降了1.64%和18.41%。因此,與運動學規劃相比,基于動力學分析的天線展開過程最優規劃可以進一步減小展開角加速度峰值和驅動功率峰值。

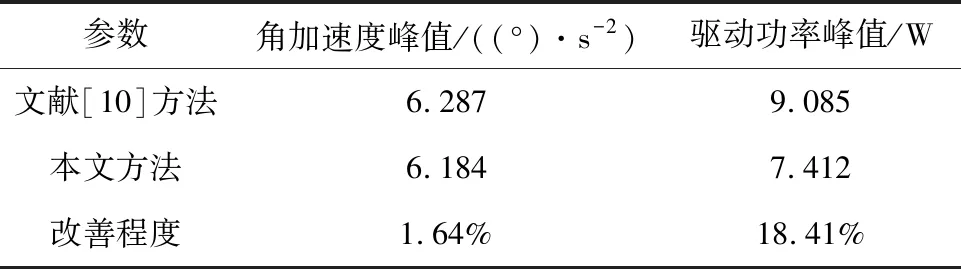
表1 非自適應策略的優化結果

3.3 基于自適應策略的展開過程規劃

為了在滿足精度的條件下,進一步提高優化效率,采用第2.2.2節的自適應策略對天線的展開過程進行最優規劃。

根據式(9),初始樣本點數目取為N0=21。同樣將基于運動學規劃方法[10]得到的控制點參數x0作為設計變量初始值。取收斂精度εi=0.001(i=1～4)整個優化過程經過11次迭代達到收斂條件,目標函數的迭代曲線如圖5所示。可知,整個優化過程中,對動力學仿真模型的調用總次數僅有43次。

圖5 自適應策略的目標函數迭代曲線

自適應策略的優化結果如表2所示,與文獻[10]相比,本文方法得到的天線展開角加速度峰值及驅動功率峰值分別下降了2.18%和18.93%。

表2 自適應策略的優化結果

3.4 結果對比

非自適應策略和自適應策略的優化結果及計算效率對比情況如表3所示。可知,在目標函數改善方面,兩種優化策略得到的結果很接近,自適應策略得到的展開角加速度峰值僅降低了0.55%,驅動功率峰值僅降低了0.63%。在計算效率方面,自適應策略對動力學仿真模型的調用次數從非自適應策略的160次減少到了43次,計算效率提高了73.12%。

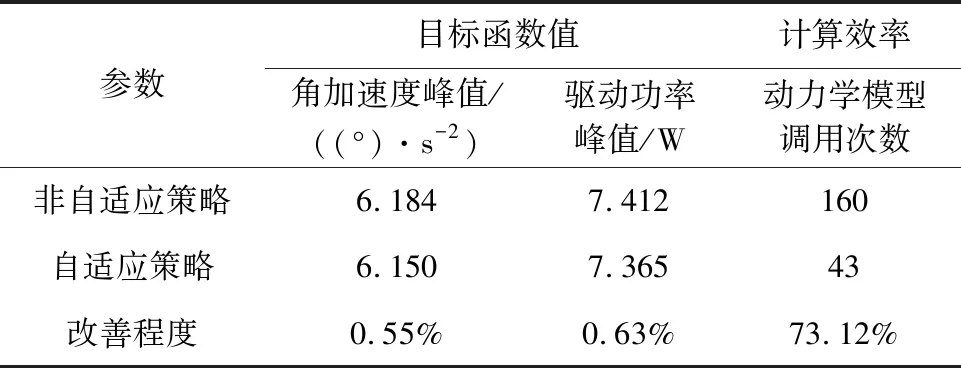
表3 不同優化策略結果對比

(17)

式中:tp為天線的展開周期,本例中tp=10 s。

將式(17)中的驅動索收納長度最優規劃作為輸入,對天線進行展開過程動力學分析,可得到天線展開過程的最優響應。優化后的天線展開角響應情況如圖6所示,驅動功率變化情況如圖7所示。

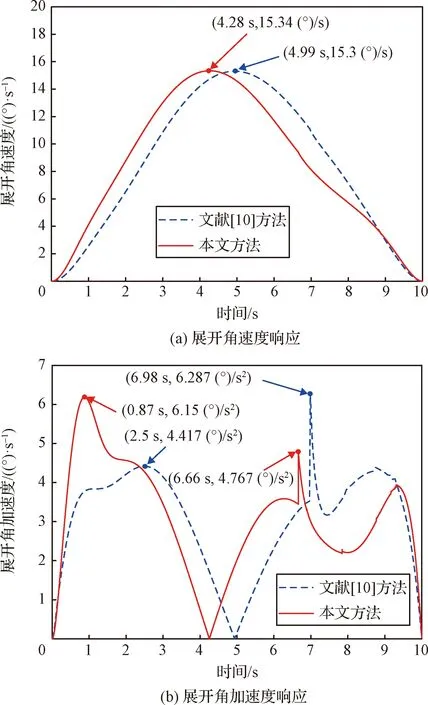
圖6 優化后的天線展開角響應情況

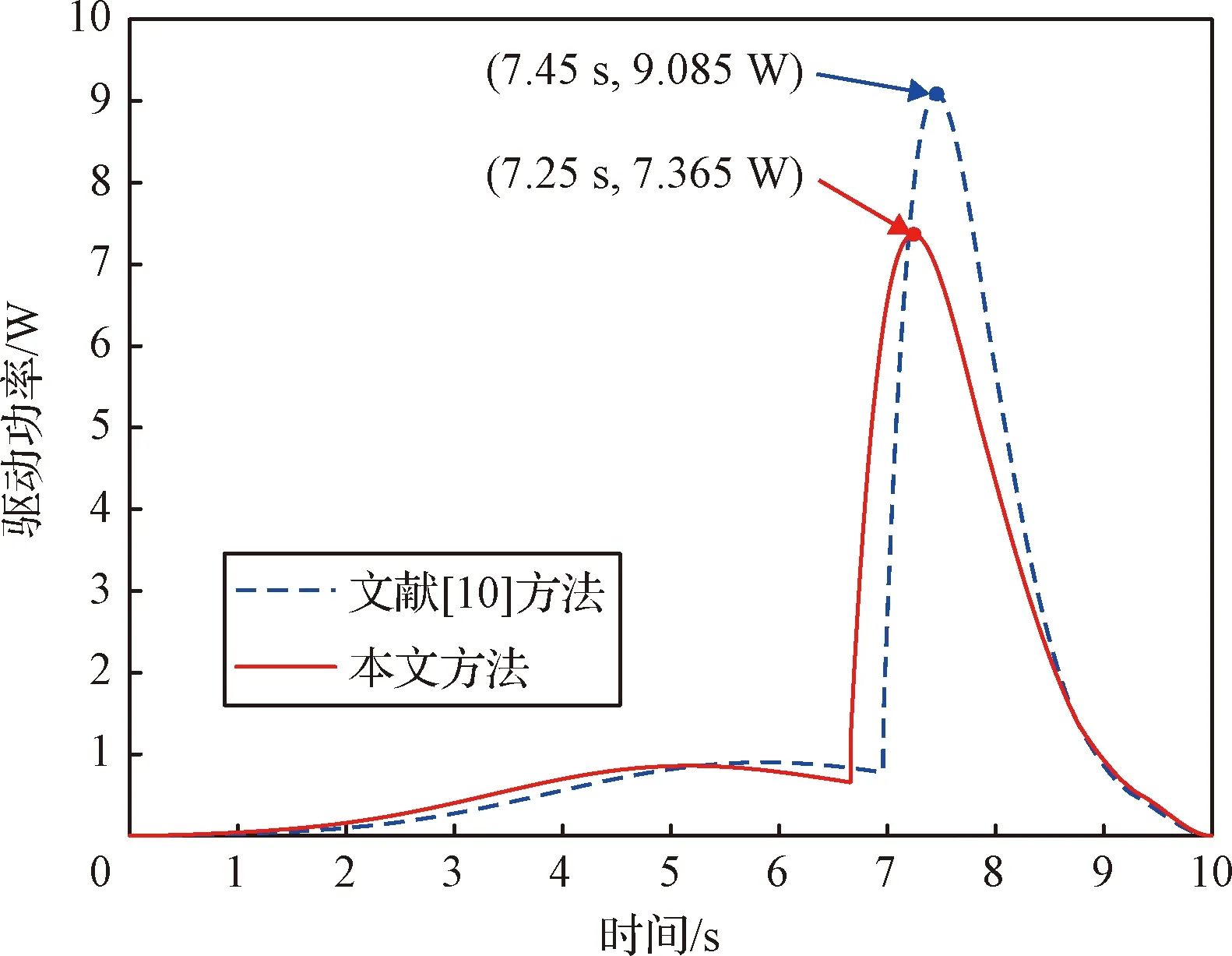
圖7 優化后的驅動功率變化情況

由圖6(a)可知,優化后天線展開角呈現先加速、后減速的運動規律,減速階段的起始時刻由優化前的4.99 s提前至4.28 s。由圖6(b)可知,加速展開階段的展開角加速度峰值比優化前增大,減速階段的角加速度峰值比優化前減小,整個過程的角加速度峰值由6.287 (°)/s2降低至6.150 (°)/s2。

由圖7可知,優化后驅動功率的變化過程均可分為兩個階段:1)索網結構松弛階段,該階段驅動繩索需要克服運動副的摩擦阻力,驅動功率隨著展開過程的先加速、后減速運動規律也呈現出先逐漸增大再減小的趨勢;2)索網結構逐漸張緊到天線完全展開階段,該階段驅動繩索需要克服摩擦阻力和索網張力的共同作用,由于該階段索網對桁架的作用力呈現先增大再減小規律[16],天線的展開速度則逐漸減小直到速度為零時完全展開,所以該階段驅動功率也呈現先增大再減小為零的趨勢。整個展開過程中,驅動功率的峰值從優化前的9.085 W降低至7.365 W。

4 結 論

本文提出了一種基于動力學分析的環形網狀天線展開過程規劃方法。基于Kriging模型構建了環形網狀天線展開過程動力學分析的代理模型,并提出了展開過程規劃的非自適應和自適應兩種優化策略。研究結果表明:

1) 通過構建環形網狀天線展開過程動力學分析的代理模型,有效解決了高精度動力學模型在展開過程規劃中帶來的高計算成本問題,實現了基于動力學分析的展開過程規劃。

2) 在傳統運動學規劃方法的基礎上,基于動力學分析的環形網狀天線展開過程規劃方法可以進一步降低天線的展開角加速度峰值和驅動功率峰值。

3)通過對比非自適應和自適應兩種優化策略可知,自適應策略減少了高精度動力學模型的調用次數,能夠在保證最優解附近代理模型精度的條件下大幅度提高優化效率。

綜上所述,基于動力學分析的環形網狀天線展開過程規劃方法可為環形網狀天線實現小沖擊、低能耗展開提供一定的實際指導作用。