基于復合材料理論的混凝土內多離子擴散模型

田壯，肖官衍，金偉良，夏晉，程新

(浙江大學 建筑工程學院，浙江 杭州 310058)

在自然環境中，氯離子侵蝕引起的鋼筋腐蝕是造成混凝土結構耐久性能下降的主要原因之一[1].濃度差引起的離子擴散是驅動有害介質侵蝕的重要因素，而離子擴散系數決定混凝土內部離子的擴散速率.

混凝土作為典型的多孔材料，離子通過孔隙內部的溶液傳輸.離子的擴散系數受到溶液中離子擴散系數和混凝土內部孔隙結構的影響.溶液中離子傳輸的本質是帶電粒子傳質的過程，因此離子擴散系數和溶液的電導率有關[2].混凝土的孔隙液中通常存在Cl-、SO42-、Na+、OH-、Ca2+、K+等多種陰陽離子，所有種類的離子共同決定孔隙液的電導率，影響孔隙液中任意一種離子的擴散速率[3]；因此，有必要考慮離子種類和濃度對離子擴散系數的影響.

混凝土是由水泥漿、骨料和界面過渡區（ITZ）構成的多相復合材料.混凝土內部的孔隙結構一方面受到水泥漿中孔隙及其空間分布的影響，另一方面與混凝土中骨料的分布有關[4].盡管骨料較致密，但骨料和水泥漿之間形成的ITZ具有較高的孔隙率.需要考慮混凝土各相相內孔隙結構的差異對混凝土內部離子擴散系數的影響.

基于多相復合材料理論的混凝土內部多離子的傳輸已成為當前混凝土內部離子傳輸研究的重點，在數值模擬領域中取得了進展[5-7].關于混凝土內部離子擴散系數的理論模型研究，Thomas等[8-12]將混凝土視為均質材料，提出單相模型.還有部分學者考慮混凝土構成組分的影響，提出由水泥漿和骨料構成的兩相模型[13-17]以及由水泥漿、骨料和ITZ構成的三相模型[18-19].這些模型中通常僅考慮單一離子擴散的情況，沒有關注多種離子傳輸時離子種類和濃度對離子擴散系數的影響.

為了解決上述問題，本文基于Nernst-Einstein方程以及離子的濃度和電導率的關系，研究溶液中離子種類和濃度對擴散系數的影響.根據通用有效介質（GEM）理論，探究考慮骨料、ITZ和水泥漿各相相內孔隙結構的混凝土內離子擴散系數.提出基于多相復合材料理論的混凝土內部多離子擴散預測模型.以常見的有害介質氯離子為例，采用該模型對其在混凝土內部的離子擴散系數進行預測，與試驗數據比較，驗證模型的有效性.

1 多離子傳輸離子擴散系數

離子在混凝土內部傳輸的本質是帶電粒子在多孔介質的孔隙內部的溶液中傳質的過程.根據Nernst-Einstein方程可知，多離子傳輸時溶液中離子的擴散系數[20]為

式中：Dliq,k為溶液中第k種離子的擴散系數，R為理想氣體常數，T為熱力學溫度，Lk為電導率的分項系數， σliq 為溶液的電導率，zk為第k種離子電荷數，F為法拉第常數，cliq,k為溶液中第k種離子的濃度.

電導率的分項系數Lk可由下式[20]計算：

式中：Ik和I分別為離子傳輸過程中第k種離子形成的電流和總電流.

離子在溶液中傳輸可以視為導體中電荷的運動：

式中：S為導體截面積，E為電場強度.

溶液的電導率[21]為

式中：σliq,k為第k種離子對應的溶液分項電導率，λk為第k種離子的當量電導率，λ0,k為第k種離子的無限稀釋溶液電導率，Gk為第k種離子的導電系數.

在電場強度相同的情況下，導體內電流密度和電導率成正比.根據式(3)可知，第k種離子對應的電流為

則有

聯立式(1)、(4)、(5)和(7)，考慮多離子擴散，溶液中離子的擴散系數為

當只考慮單離子擴散時，往往忽略離子濃度對擴散系數的影響，式（8）可以簡化為

為了研究多離子傳輸對溶液內離子擴散系數的影響，分以下2種情況對離子擴散系數進行討論：1)考慮單離子的擴散；2)考慮多離子的擴散.以含氯離子的溶液為例，Cl-的電導率參數為zkλ0,k=7.64×10-3S·m2/mol，Gk= 0.548 (mol/L)-0.5[22].

為了探究模型的有效性，將考慮單離子和多離子擴散時溶液內的氯離子擴散系數的計算值和試驗值進行比較[3,23-25].為了針對不同種類的氯鹽統一比較，采用等價氯離子濃度.以同樣為1 000.0 mol/m3的NaCl和BaCl2溶液為例，NaCl溶液中由于Na+和Cl-的濃度以及電荷數的平方均相同，根據式(8)有，即濃度為1 000.0 mol/m3的NaCl溶液中Na+和Cl-可以換算成濃度為2 000.0 mol/m3的等價氯離子.在BaCl2溶液中，由于Cl-和Ba2+濃度分別為2 000.0和1 000.0 mol/m3，同時Ba2+的電荷數平方為Cl-的4倍.根據式(8)有

濃度為1 000.0 mol/m3的BaCl2溶液中Ba2+和Cl-可以換算成濃度為6 000.0 mol/m3的等價氯離子.

如圖1所示，僅考慮單離子擴散，氯離子擴散系數恒為2.00×10-9m2/s，和稀溶液中的氯離子擴散系數2.03×10-9m2/s高度符合[26].考慮多離子擴散，當等價氯離子濃度較低時，氯離子擴散系數接近2.00×10-9m2/s.氯離子擴散系數隨著等價氯離子濃度的上升而持續下降，當等價氯離子濃度從1.0 mol/m3上升至1 000.0 mol/m3時，氯離子擴散系數下降了大約25%.試驗數據表明，氯離子擴散系數隨著等價氯離子濃度的上升而持續下降.當等價氯離子濃度從1.0 mol/m3上升至1 000.0 mol/m3時，氯離子擴散系數下降了16%；因此，溶液中離子濃度對擴散系數有著明顯的影響，兩者為負相關關系.

圖1 溶液中離子擴散系數模型預測結果和試驗數據的比較Fig.1 Comparison of predicted results of ion diffusion coefficient model in solution and experimental data

2 基于多相復合材料理論的混凝土內部離子擴散系數

混凝土是由水泥漿、ITZ和骨料構成的多相復合材料，而離子主要通過各相相內的毛細孔中的溶液進行傳輸.混凝土內部離子的擴散系數計算可以分為以下2個步驟.1)根據毛細孔內部的溶液中離子擴散系數和混凝土各相相內的毛細孔孔隙率，分別計算水泥漿、骨料和ITZ內部的離子擴散系數.2)通過計算獲得的混凝土各相相內離子擴散系數及各相體積分數，得到混凝土內部離子擴散系數.

2.1 基于多相復合材料理論的離子擴散系數模型

關于兩相復合材料的性質計算，Mclachlan等[27]提出GEM理論模型：

式中：φ為高電導率相介質的體積分數，σl、σh和σm分別為低電導率相介質、高電導率相介質和復合材料的電導率，texp為指數參數，φc為臨界體積分數.

式（10）的解析解[28]為

根據式(1)，有[28]

式(10)可以改寫為[28]

式中：Dl、Dh和Dm分別為低擴散系數相介質、高擴散系數相介質和復合材料內部離子擴散系數.

式（14）為基于GEM理論的復合材料內部的離子擴散系數模型.若Dl= 0，則

在GEM理論模型中，指數參數texp及臨界體積分數φc的取值與構成復合材料的介質的形狀大小等因素有關.texp和φc隨著介質的形狀變化，會對復合材料的Dm產生影響.關于texp的取值，Mclachlan等[27,29]采用連續滲流理論研究發現，絕大部分復合材料中texp的取值為1.46～2.00，指出較高的texp意味著介質的形狀較極端.Luo等[30]研究薄片狀的介質，指出針對這種介質的texp一般大于2.0.關于φc的取值，Lin等[31]針對球狀介質進行研究，指出φc高度依賴于介質的形狀，當形狀為正球形時，φc的取值最大.Li等[32]利用模擬的方法，指出φc和多孔材料中孔隙的連通度呈現線性關系.Xu等[33]利用連續滲流理論研究發現，在介質的形狀分別為四面體、六面體和球體等情況下，φc為0.15～0.29.

由于φc和texp的變化范圍較大且會影響Dm，對φc和texp與Dm之間的關系進行探究.

當Dl=0時，texp=1.5～5.5（φc=0.2）和φc=0.1～0.9（texp=2）對Dm的影響如圖2所示.如圖2（a）所示，當φ相同時，Dm隨著texp的增加而減小，即texp和Dm為負相關關系.如圖2（b）所示，當φ相同時，Dm隨著φc的增加而減小，即φc和Dm為負相關關系.

圖2 不同參數取值時復合材料內部離子擴散系數的變化Fig.2 Variations of ionic diffusion coefficient in composite with different parameter values

在GEM理論模型中，Dh/Dl影響Dm的計算結果.當Dl較小時，可以將Dl簡化為0，但是需要規定合理的簡化范圍.假定φ為0.2～0.9（texp=2，?＞φc=0.18），當不將Dl簡化為0時，設Dl=1且Dh=n，在n從10上升到1010的情況下，復合材料內部的離子擴散系數記為Dm1；當將Dl簡化為0時，設Dl=0且Dh=n，在n從10上升到1010的情況下，復合材料內部的離子擴散系數記為Dm2.如圖3所示為Dm1/Dm2隨著n的變化.

圖3 各相擴散系數取值不同時復合材料內離子擴散系數的變化Fig.3 Variations of ionic diffusion coefficient in composite with different diffusion coefficients in phases

如圖3所示，當φ=0.2且n=10時，在條件1的情況下，Dl=1，Dh=10，Dm1=1.84；在條件2的情況下，Dl=0，Dh=10，Dm2=0.022 7.在2種條件下，Dm1/Dm2=81.10，若將Dl簡化為0，則會造成計算結果的巨大差異.Dm1/Dm2隨著n的增大而逐漸減小，當n=108時Dm1/Dm2=1.02，2種條件下的Dm近似相等.當φ=0.1（φ＜φc=0.18）時，在條件1的情況下，Dm1隨著n的增加而緩慢增長，并逐漸趨于穩定；在條件2的情況下，Dm2恒為0，且和n無關.

綜上所述，texp和φc對Dm的影響明顯，呈現負相關關系.當φ＞φc且Dh/Dl＞108時，可以將Dl簡化為0；當φ＜φc時，不可將Dl簡化為0，否則Dm恒為0.

2.2 水泥漿、ITZ和骨料內部離子擴散系數

由于骨料較致密離子的傳輸難以進行，骨料中離子擴散系數通常簡化為0[4-5].水泥漿和ITZ均是多孔介質，因此可以視為由高擴散系數相介質（毛細孔內部溶液，其中離子擴散系數取水溶液中的離子擴散系數，例如室溫下氯離子在無限稀釋溶液中的離子擴散系數為2.03×10-9m2/s）和低擴散系數相介質（固相，值得注意的是水泥漿的固相中存在孔隙，例如C-S-H凝膠孔，因此離子擴散仍然可以進行）組成的兩相復合材料，采用GEM理論模型對水泥漿內部離子擴散系數進行求解[28].Christensen等[34]研究指出，當水泥漿中的毛細孔孔隙率φcem＜ 0.4時，texp= 5.8.φcem和水灰質量比mw/mc及水泥漿的水化程度m有關[35]：

水泥漿的最終水化程度[36]為

根據式（17）的計算可知，當水灰質量比為0.2～0.55時，水泥漿水化完成后φcem均小于0.4，則texp取5.8.根據研究可知，水泥漿的臨界體積分數φc=0.18[37]，代入式(14)可得

式中：Ds,k、Dliq,k和Dcem,k分別為水泥漿固相、毛細孔內部溶液以及水泥漿中第k種離子的擴散系數.

毛細孔內部溶液和水泥漿固相中的離子擴散系數差異較大，令Ds,k/Dliq,k=p，式（18）的解析解為

關于ITZ的texp和φc，Bentz等[38]研究指出可以直接取水泥漿中的參數，則ITZ中的離子擴散系數為

式中：DI,k為ITZ中第k種離子的離子擴散系數，φI為ITZ的毛細孔孔隙率.

2.3 混凝土內部離子擴散系數

水泥漿和骨料之間形成ITZ，可以看作骨料被ITZ相包裹，將骨料和ITZ視為骨料-ITZ相.骨料形狀簡化為球體，可以采用Bruggeman非對稱介質理論（該理論是GEM理論的特殊形式[27]）計算骨料-ITZ相內的離子擴散系數DI-A,k：

式中：φITZ和φA分別為ITZ和骨料的體積分數.

骨料-ITZ相散布在水泥漿中，將混凝土簡化為兩相復合材料，可以采用GEM理論計算混凝土內部離子擴散系數.目前，對于混凝土的GEM理論參數研究較少，但是根據Xu等[33]的數值模擬研究可知，在三維空間中，當介質形狀為球體時，texp=2，φc=0.29.令骨料-ITZ相和水泥漿中離子擴散系數的比值q=DI-A,k/Dcem,k，則混凝土內部離子擴散系數Dcon,k為

3 離子擴散系數預測模型的建立

擴散預測模型的建立過程分為以下3個步驟.1)計算多離子傳輸時毛細孔內部溶液中離子的擴散系數Dliq,k.2)通過Dliq,k、φcem 和φI ，分別計算Dcem,k和DI,k.3)通過混凝土各相相內離子擴散系數及各相的體積分數，計算得到混凝土內部離子擴散系數.

1)毛細孔內部溶液中的離子擴散系數.根據式(8)可知，多離子傳輸時毛細孔內部溶液中離子的擴散系數為

2)混凝土各相相內離子擴散系數.由于骨料較致密，通常考慮孔隙率和離子擴散系數為0.水泥漿和ITZ為多孔介質，根據式(16)、(17)可知，φcem和mw/mc有關：

相較于水泥漿，ITZ的毛細孔孔隙率較大.根據以往的理論研究和試驗結果[28,39-40]，取1.5倍的φcem ：

將式(26)～(28)代入式(19)、(21)，水泥漿和ITZ內部離子擴散系數Dcem,k和DI,k分別如下：

根據式(20)、(22)可知，mφcem和mφI分別為

3)混凝土內部離子擴散系數.根據式(23)、(30)可知，骨料-ITZ相內部離子擴散系數DI-A,k為

φA可以通過混凝土配合比獲取，φITZ受到骨料級配曲線及ITZ厚度tITZ的影響[41]，

式中：φr為骨料粒徑為dr的骨料的體積分數.

將式(29)、(33)代入式(24)，考慮多離子擴散時，混凝土內部離子擴散系數為

根據式(25)可知，mVI-A為

建模流程如圖4所示.模型計算過程中須輸入離子的無限稀釋溶液電導率λ0,k、離子的導電系數Gk、cliq,k、p、mw/mc、ITZ厚度tITZ及骨料級配曲線.當只考慮單離子擴散時，毛細孔內部溶液中的擴散系數Dliq為

圖4 混凝土內多離子擴散模型的建模流程圖Fig.4 Modeling flow chart of diffusion model of multi ions in concrete

水泥漿和ITZ內部離子的擴散系數分別如下：

混凝土內部離子的擴散系數為

4 模型驗證和分析

為了探究離子擴散預測模型的有效性，驗證了Yang等[41]的氯離子擴散系數測定試驗，并將模型得到的計算結果和試驗結果進行比較.試件是直徑為100 mm、厚度為50 mm的圓柱體，如圖5所示.試件的水灰質量比為0.4，骨料的體積分數分別為0、10%、20%、30%和40%.骨料的級配曲線如表1所示.表中，wr為骨料粒徑為dr的骨料的質量分數，由于本試驗中僅存在一種細骨料，可以忽略骨料的密度變化，此時體積分數等于質量分數，即φr=wr.在試驗過程中，混凝土試件的兩端分別放置質量分數為3.0%（濃度約為500 mol/m3）的氯化鈉溶液和300 mol/m3的氫氧化鈉溶液，混凝土孔隙液飽和.在試驗過程中，待陽極池中氯離子通量穩定時，測量混凝土內部氯離子的擴散系數.另外，tITZ取值為20 μm.

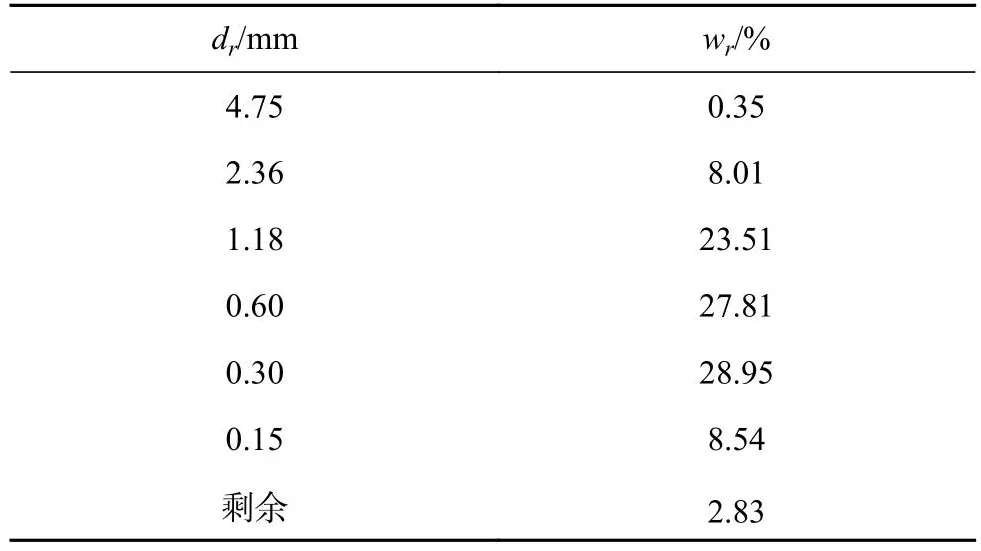
表1 骨料級配Tab.1 Grading of aggregate

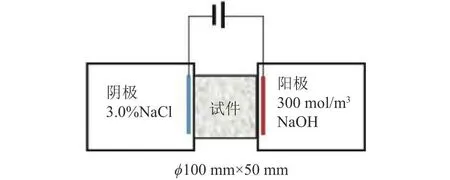
圖5 氯離子擴散系數測定試驗裝置的示意圖Fig.5 Schematic diagram of chloride ion diffusion coefficient measurement experiment

模型中參數取值如下：λ0,Cl-=7.64×10-3S·m2/mol和GCl-=0.548 (mol/L)-0.5[22]，cliq,Cl-=cliq,Na+=500 mol/m3，p=1×10-5[28]，mw/mc=0.4，tITZ=20 μm.

當僅考慮單離子擴散時，根據式(37)計算可知，毛細孔內部溶液中的氯離子的擴散系數Dliq,Cl-= 2.00×10-9m2/s.根據式(38)、(39)計算可知，水泥漿和ITZ內部的氯離子擴散系數分別為Dcem,Cl-=3.07×10-12m2/s，DI,Cl-=14.38×10-12m2/s.DI,Cl-約為4.7倍的Dcem,Cl-，較符合文獻[4,42,43]中DI,Cl-/Dcem,Cl-≈5的研究結果.根據式(40)計算可知，混凝土內部氯離子擴散系數Dcon,Cl-隨骨料體積分數的變化如圖6所示.Dcon,Cl-隨著φA的上升而減小，φA從0上升到40%，Dcon,Cl-減少了37%.此時，Dcon,Cl-的計算值約為試驗值的1.5倍.

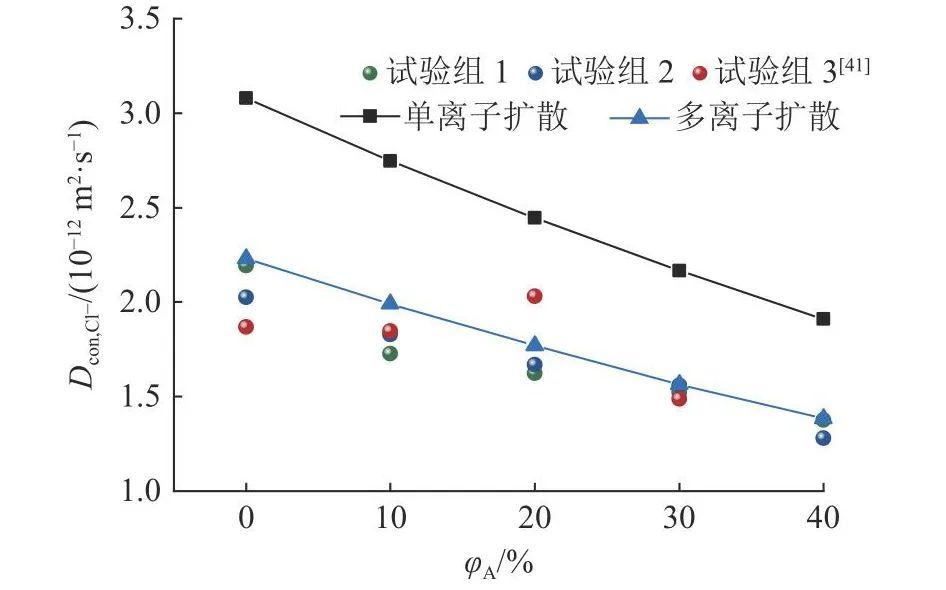
圖6 氯離子擴散系數計算值和實驗值的對比Fig.6 Comparison of calculated values and test values of chloride ion diffusion coefficient

當考慮多離子擴散時，將濃度為500.0 mol/m3的氯離子和鈉離子代入式(35)計算.與僅考慮單離子擴散相比，氯離子的擴散系數下降了大約25%，該計算結果更加符合試驗值.

將本文模型和表2中的兩相[13-17]及三相[18-19]離子擴散系數模型進行對比，結果如圖7所示.表中，φl和φh分別為基體和基底體積分數，Dcem和DI分別為水泥漿和ITZ內的離子擴散系數，ε為ITZ厚度與骨料半徑的比值.圖中，模型1～5為兩相模型，模型6、7為三相模型.兩相模型的計算過程分成以下2步.1)將水泥漿中的毛細孔溶液和固相分別視為高擴散系數相介質和低擴散系數相介質，計算水泥漿中的離子擴散系數.2)將水泥漿和骨料分別視為高擴散系數相介質和低擴散系數相介質，計算混凝土內部的離子擴散系數.三相模型無法根據模型自身計算水泥漿和ITZ內部離子的擴散系數，采用本文模型得到Dcem,Cl-=3.07×10-12m2/s，DI,Cl-=14.38×10-12m2/s.

表2 擴散系數模型的概述Tab.2 Overview of diffusion coefficient model

圖7 不同氯離子擴散系數模型的預測值對比Fig.7 Comparison of prediction result of different chloride ion diffusion coefficient models

結果表明，除模型3以外，利用其余的兩相模型計算得到的氯離子擴散系數遠高于實驗值.模型3的計算值大約為試驗值的2倍，存在較大的差距.三相模型7中離子擴散系數隨著骨料體積分數的增加而上升，和試驗結果相反.相較于兩相模型，本文模型的計算結果和試驗結果更接近，計算結果更合理.本文提出的模型可以通過混凝土中的離子種類和濃度，計算水泥漿和ITZ內部的離子擴散系數.傳統的三相模型需要通過其他模型或實驗數據，得到水泥漿中的離子擴散系數.

5 結 論

（1）根據GEM理論和Nernst-Einstein方程以及離子濃度和電導率的關系，建立基于多相復合材料理論的混凝土內部多離子擴散預測模型.

（2）離子濃度和擴散系數為負相關關系，考慮離子濃度的影響有利于提高離子擴散預測模型的精度.

（3）采用GEM理論，計算復合材料內部離子擴散系數.當高擴散系數相介質的體積分數大于臨界體積分數，且高擴散系數相介質和低擴散系數相介質的內部離子擴散系數比值大于108時，可以將低擴散系數相介質內部離子擴散系數簡化為0.當高擴散系數相介質的體積分數小于臨界體積分數時，不可將低擴散系數相介質內部離子擴散系數簡化為0，否則復合材料內部離子擴散系數的計算結果恒為0.

（4）本文提出的離子擴散系數模型相較于傳統的兩相模型，該模型的模擬結果和試驗結果更接近，計算結果更合理.相較于三相模型，該模型可以通過離子的種類和濃度直接計算混凝土內部的離子擴散系數.