圓錐曲線問題中“非對稱韋達定理”的處理策略*
2023-08-26 03:45:06福建省南安五星中學362300莊津津
中學數學研究(江西) 2023年9期
福建省南安五星中學 (362300) 莊津津
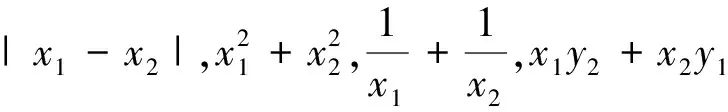
一、典例分析
基于下述典型問題,我們多個角度進行分析,介紹圓錐曲線問題中“非對稱韋達定理”的幾種常見的處理策略.
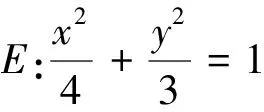



在上述解題過程中,我們通過重建坐標關系,把非對稱性結構轉化成韋達定理的結構,實現整體代入求解.
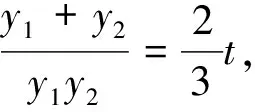

評注:解法一,借助從特殊到一般,先猜想后證明,用分析法轉化不對稱運算為對稱運算,回歸韋達定理.解法二利用點在橢圓上尋找并重建坐標關系.解法三、四,通過韋達定理進行消元減元,減少變量個數,從而達到化簡目的.上述的四種解法都是“非對稱”韋達定理的常見解題方法.通過上述例題我們也能感受到,消參方法和直線方程形式的選擇,對后續的計算處理將產生不同的影響,計算量也存在較大差異,需根據問題的特征,合理進行選用.
二、類題賞析
為體驗上述四種方法在解決此類問題的應用,我們提供下述三道習題,供讀者賞析.
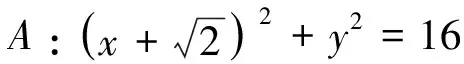
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
兒童故事畫報(2019年5期)2019-05-26 14:26:14
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12

