基于卷積循環神經網絡的混凝土壩變形預報

蔣佳彤, 李明偉, 尚憲朝, 耿敬

(1.黑龍江大學 水利電力學院,黑龍江 哈爾濱 150006; 2.哈爾濱工程大學 船舶工程學院,黑龍江 哈爾濱 150001; 3.海洋石油工程股份有限公司, 天津 300452)

大壩運行過程中,在防洪、發電、航運、灌溉等方面發揮著重要的作用,大壩的運行狀況也關乎著周邊環境的生命安全、生態安全和財產安全。由于混凝土壩具有抗震性好、安全、泄洪方便等優點,在我國得到了廣泛的應用[1]。變形是目前公認能夠有效綜合反映大壩運行狀態的典型效應量[2],建立有效、精準的變形監測模型,研究混凝土壩在運行過程中的變形規律,加強混凝土壩變形的安全監測是壩工事業的重點內容。

傳統的監測模型是假設大壩的變形效應量與各個影響因素之間呈線性關系,而實際上,大壩的變形效應量與各個影響因素之間呈復雜的非線性關系,降低了模型的預測性能。隨著人工智能理論的發展,人工神經網絡(artificial neural network,ANN)由于具有很強的非線性映射能力和自適應學習能力,在大壩變形分析中得到了較為廣泛的應用[3-4]。ANN在處理不確定性及非線性等問題上顯現出巨大的優勢,但其具有收斂速度慢、易陷入局部最優、網絡結構難以確定等問題[5]。

近年來,深度神經網絡因具有更強大的特征學習能力得到了高速發展和廣泛使用[6]。卷積神經網絡(convolutional neural network,CNN)由于具有局部連接和權值共享等特點,已成為深度學習領域中最成功的算法之一,在處理時間序列數據的問題中,常將卷積神經網絡與循環神經網絡相結合使用。門控循環單元神經網絡(gate recurrent unit,GRU)是循環神經網絡的特殊形式,模型簡單,參數少且不容易過擬合,可充分挖掘時間序列數據的非線性關系,在各個領域取得了不錯的效果。Gupta等[7]提出了基于CNN和GRU的方法,建立分析顧客行為的自動化系統,結果表現良好;周海南[8]建立了基于GRU和CNN的水位智能預測模型,實現了內河水位的預測;趙兵等[9]提出了基于注意力機制的CNN-GRU模型,來實現短期電力負荷的預測;Yu等[10]提出了一種基于CNN與GRU相結合的菇房多點溫濕度預測方法,并取得較高的預測精度;趙全明等[11]提出了CNN-GRU集成深度模型,用于預測玉米根區不同深度土壤含水量,提供灌溉依據。

本文針對大壩變形時間序列的強非線性,設計了基于CNN和GRU的深度學習組合模型,提出了CNN-GRU混凝土壩變形預測方法。

1 CNN-GRU大壩變形預測模型構建

1.1 卷積神經網絡

卷積神經網絡[12]具有權值共享和局部連接的特點。權值共享是指其中某個神經元的權值參數可以與其他神經元共享,減少了參數。局部連接是指卷積層的節點不再與前一層所有的節點連接,而是與部分節點進行連接,可減少神經網絡的參數個數。由于卷積神經網絡具有的這2種特點使得模型訓練速度提高,有效地避免過擬合。

CNN的卷積層是卷積神經網絡的核心部分,卷積層的輸入可以是輸入層的輸入數據,也可以是經過池化處理后得到的數據。卷積過程為:

ci=f(ci-1?fi+bi)

(1)

式中:ci-1為卷積層的輸入矩陣;fi為卷積核的權矩陣;bi為偏置值;f(x)為激勵函數,以提高CNN的非線性能力。

池化層也稱為下采樣層,用來降低上一層的空間維度,使其結果參數減少,增加了網絡的稀疏性,但網絡深度并不改變,可在一定程度上防止網絡過擬合。一般采用平均值池化法或最大值池化方式得到特征圖。CNN的全連接層在卷積神經網絡的最后,防止局部連接的特征丟失,將經過卷積和池化后學習到的特征結果進行組合與推斷,形成利于分類的特征,最后將結果輸出,運算過程與淺層的神經網絡的運算方式相同。

1.2 門控循環單元

門控循環單元是循環神經網絡的一種特殊形式,是長短時記憶網絡LSTM的一種變體,旨在解決標準RNN梯度爆炸或丟失問題,同時保留長期序列信息。GRU[13]是基于 LSTM 的結構基礎,把LSTM的3個門結構簡化為2個門結構,即刪除遺忘門,保留重置門和更新門,使得參數量減少,具有更簡單的模型結構,減少訓練時間,提高模型計算效率。GRU的內部結構如圖1所示。

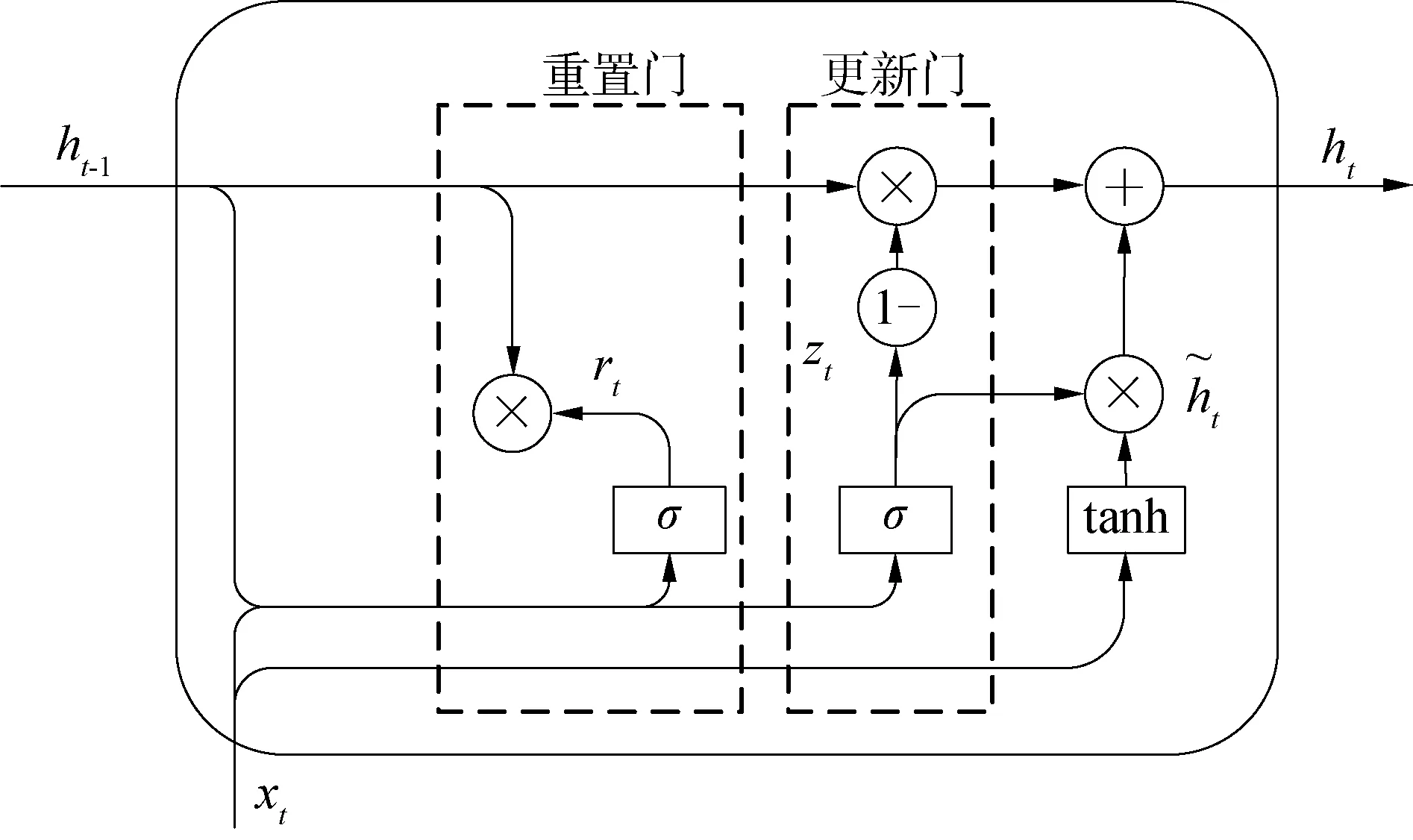
圖1 GRU網絡結構Fig.1 GRU network structure

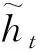
rt=σ(Wr[ht-1,xt])

(2)

(3)

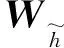
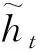
zt=σ(Wz[ht-1,xt])

(4)

(5)

式中:zt表示更新門;Wz表示更新門權重矩陣。

1.3 CNN-GRU變形預測模型

為了對大壩變形情況進行精準預測,本文將卷積神經網絡與門控循環單元相結合,建立基于CNN-GRU的混凝土壩變形監測模型。

1.3.1 確定各層參數

本文旨在利用CNN提取大壩監測數據的空間相關特征,再送入GRU層進一步挖掘變形序列變化趨勢,因此使用一維卷積神經網絡。

1)輸入層。為了耦合影響大壩變形的特征信息,充分挖掘這些特征的時間、空間特征規律,將大壩的歷史變形量和相關的特征數據構成一個新的時間序列特征向量,作為CNN-GRU變形預測模型的輸入數據。

2)CNN層。CNN層主要對大壩的歷史變形數據進行特征提取,使用一維卷積神經網絡挖掘大壩變形監測數據的空間相關特征,再送入GRU層進一步提取變形序列變化趨勢。經過反復優化模型,將卷積層數定為2,卷積核的數量定為16,大小為6時模型精度最高。選擇最大池化法對提取的高維特征進行降維,將提取的特征作為GRU層的輸入。

3)GRU層。主要負責從CNN層所提取的特征中學習變形的變化規律,經反復優化,構建1層GRU結構時可達到最好預測效果,激活函數采用Tanh,最后通過全連接層處理,反歸一化后得到大壩變形預測值。

1.3.2 激活函數的選擇

混凝土壩變形量與變形因子之間具有復雜的非線性關系,需要在神經網絡模型中添加激活函數引入非線性,使神經網絡模型能夠更好地學習變形量與變形因子之間的非線性關系。常用的激活函數主要有sigmoid函數、Tanh函數、Relu函數[15]等。

Sigmoid函數是在神經網絡模型中最常用的激活函數,函數輸出值(0,1),在函數圖像斜率大的地方,類似神經元的敏感區,在函數圖像兩側的平緩區,類似神經元的抑制區。Sigmoid函數由于涉及很多冪運算,所以計算時較繁瑣,會增加模型的訓練時間。同時,在深度神經網絡結構中,涉及的參數較復雜,容易造成梯度消失和梯度爆炸問題。ReLu函數在近幾年中比較普遍用,在正區間內有效地解決了梯度消失問題。而且ReLu函數沒有指數運算,可極大地提高計算速度。但ReLu函數在反向傳播過程中,如果輸入為負時,梯度完全為0。且ReLu函數不是以0為中心的函數,在使用時,容易導致權重更新緩慢。Tanh函數,也叫雙曲正切函數,函數以0為中心,輸出值(-1,1)。Tanh函數相較于Sigmoid函數收斂速度較快,在本文中,采用Tanh函數作為激活函數。

2 混凝土壩工程實例預測

為驗證CNN-GRU模型的預測精度,本文以實際混凝土壩工程為例,進行分析研究。根據已有的大壩理論知識[16],大壩變形監測中主要考慮由水壓、溫度以及時效引起的變形,在本文中,影響混凝土壩變形量的水壓分量取上游水位H、H2、H3;溫度分量取sin(2πkt/365)、cos(2πkt/365)、k=(1,2),t為從起始日開始的累計天數;時效分量取θ、lnθ,其中θ=0.01t。因此,混凝土壩變形量與影響因素之間的函數關系為:

(6)

本文選取該壩其中某一測段的264期監測數據,以1～234期數據作為訓練樣本,235～264共30期數據作為測試樣本。為評價CNN-GRU變形預測模型的性能,分別建立了BP神經網絡模型、CNN模型、LSTM模型和GRU模型進行對比分析,各模型的預測值和殘差值見圖2、3。

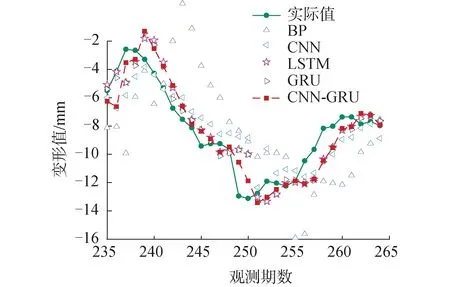
圖2 模型的預測值和實際值對比Fig.2 Comparison between predicted and actual values of the model

由圖2實際值的變化曲線可看出,大壩變形序列波動變化較劇烈,主要呈非線性變化,具有很強的變化隨機性。如果用單純的統計變形模型很難實現變形值的精確預測。在所有預測曲線中,BP神經網絡模型偏離實際變形值最大,誤差較大。而基于CNN-GRU的預報模型相對于其他3種模型的預測效果更好。從整體預測趨勢看,大壩變形值在第245期以后出現較大波動,此時,BP和CNN網絡模型所得的預測值與大壩實際變形趨勢的誤差較大。LSTM模型和GRU模型預測精度相比于前2種模型更接近實際值,但是仍存在較大誤差。而CNN-GRU模型結合CNN和GRU的優勢,能有效地學習輸入數據中的特征和規律,更好地預測出大壩變化曲線,誤差最小。

由圖3的殘差對比可以看出,BP神經網絡模型的最大殘差為-8.181 9,最小殘差為-0.281 1;CNN神經網絡模型的最大殘差為-4.216 6,最小殘差為0.082 2;LSTM神經網絡模型的最大殘差為-3.137 3,最小殘差為0.036 8;GRU神經網絡模型的最大殘差為-3.254 9,最小殘差為-0.098 9;而本文提出的CNN-GRU神經網絡模型的最大殘差為2.509 8,最小殘差為-0.064 5,且能保證更好的全局預測精度,更有利于提高大壩的變形預測精度。綜合分析結果表明,CNN-GRU模型在大壩變形預測中取得了更好的預測效果。

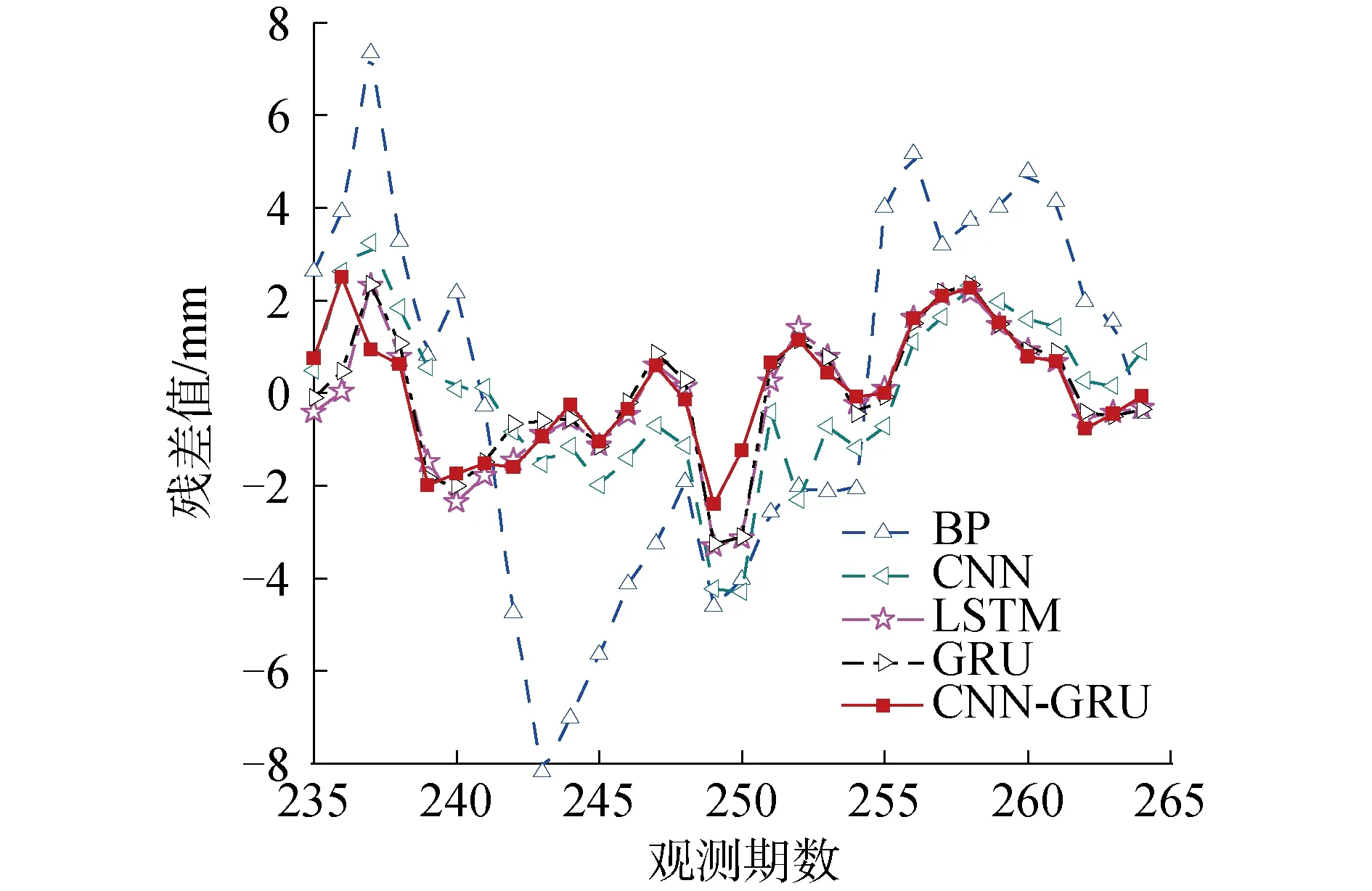
圖3 模型的預測殘差對比Fig.3 Comparison of prediction residuals of models

為了進一步比較所建模型對大壩變形預測的準確性和穩定性,本文選取均方根誤差(root mean square error,RMSE)、平均絕對誤差(mean absolute error,MAE)、平均絕對百分誤差(mean absolute percentage error,MAPE)作為模型性能評價的指標。評價指標表示預測數據的誤差情況和相對偏離程度,值越小表示預測效果越好、預測精度越高。

(7)

(8)

(9)

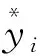
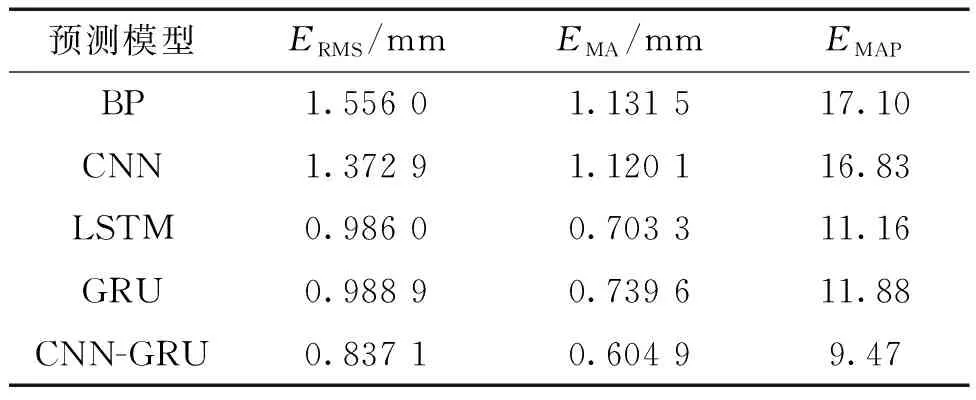
表1 不同預測模型的性能指標對比Table 1 Comparison of performance indicators of different prediction models

從表1中可以看出,相比于BP、CNN、LSTM和GRU預測模型,CNN-GRU的ERMS分別降低了0.718 9、0.535 8、0.148 9、0.151 8;EMA分別降低了0.526 6、0.515 2、0.098 4、0.134 7;EMAP分別降低了7.63、7.36、1.69、2.41。由此可知,CNN-GRU模型的預測值與實際大壩位移變形值更加接近,預測效果更好,能夠更好地預測大壩位移的變化趨勢。從整體預測趨勢看,預測值在第245期以后出現較大差異,為更詳細比較各模型預測性能,將預測結果列于表2。

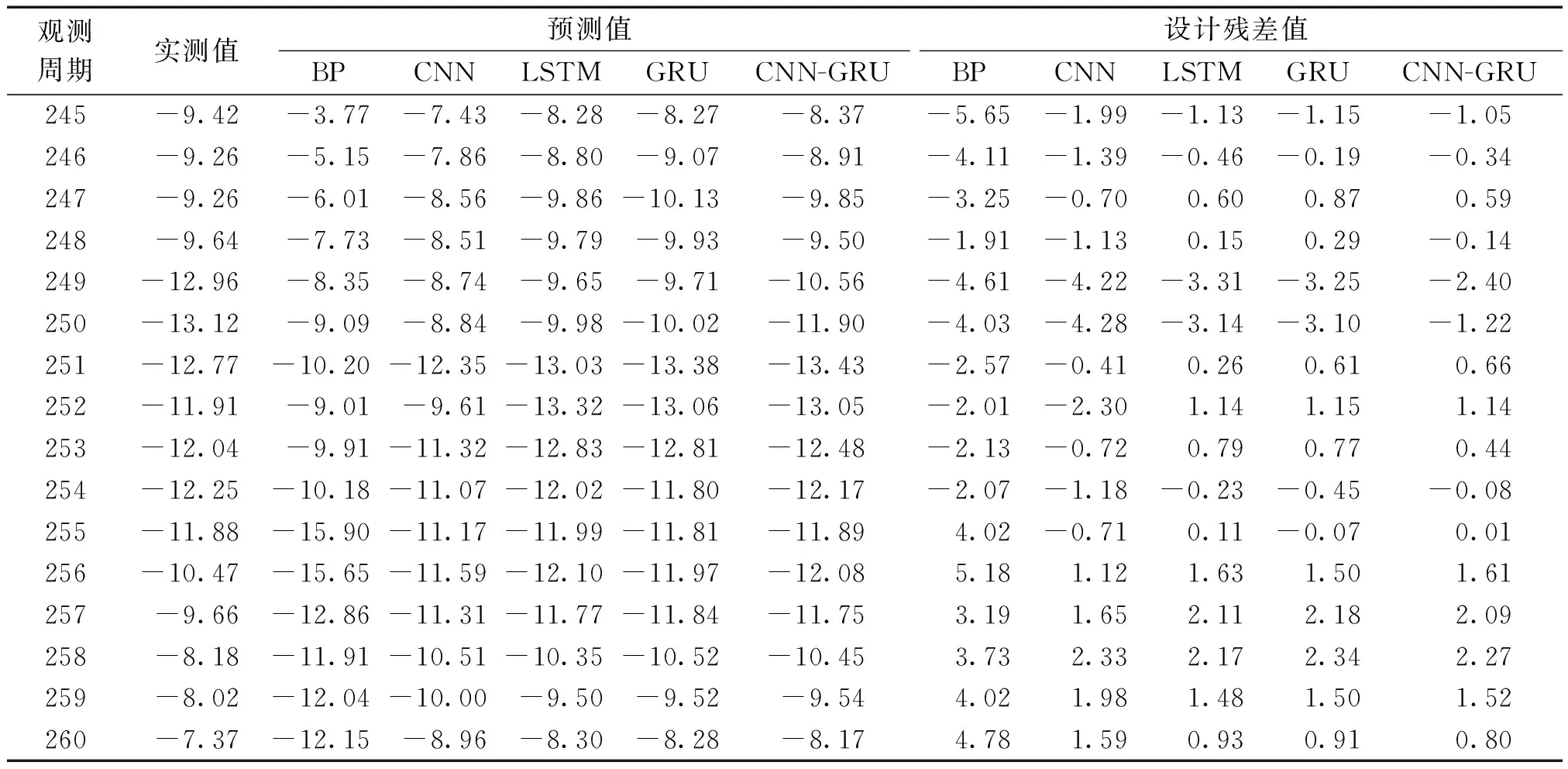
表2 模型部分預測結果Table 2 Model part prediction results mm

由表2可得出,在變化波動幅度較大這幾期,BP神經網絡模型所得的預測值誤差最大,很難準確預測出大壩實際變形趨勢;CNN模型預測值比實際值偏小,誤差較大;LSTM模型和GRU模型預測精度相比于前2種模型更接近實際值,但是仍然存在誤差較大的情況;而CNN-GRU模型能更好地預測出大壩變化曲線,誤差最小。由此可得,在不同模型預測值差異較大的15期數據中,CNN-GRU的預測結果精度最高。綜合分析結果表明,CNN-GRU模型在大壩變形預測中取得了更好的預測效果。

3 結論

1)本文建立的基于CNN-GRU的混凝土壩變形預測模型,充分利用了CNN和GRU的優勢,深度挖掘數據在時間和空間上的特征規律,更好地預測大壩變形量與各影響因素之間的非線性關系。

2)工程實例表明,該模型與BP神經網絡模型、CNN模型、LSTM模型、GRU模型相比,本文的方法能夠獲得更高的大壩變形量預測精度,預測值與大壩實際變形值更接近,是一種更先進的大壩變形預測模型。

3)本研究建立的大壩變形監測模型,除可應用于混凝土壩外,還可以研究拓展應用于其他壩體結構,可為大壩智能管理系統提供技術支撐。