基于Archard理論的浮動密封結構磨損特性試驗研究*

高俊峰,李 偉,靳衛華,吳 磊,明 友

(合肥通用機械研究院有限公司,安徽 合肥 230031)

0 引 言

目前,管線平板閘閥已經被廣泛應用于燃氣管線、輸油管線等長距離傳輸管線中。該閥門的關鍵密封結構主要包括:閥桿動密封結構和浮動閥座-閘板密封結構[1]。其中,閘閥的磨損壽命在極大程度上取決于浮動閥座-閘板密封副(簡稱:浮動密封結構)的耐久性。在長距離輸送管線上及產油量較大時期,原油的沖刷、雜質的累積以及復雜的幾何結構設計,都會導致閘閥浮動密封結構磨損嚴重,使其密封結構失效,導致事故頻發[2]。

目前,ABAQUS仿真分析軟件[3]已廣泛被研究人員用于處理各行各業中的高度非線性問題。國內外學者利用該仿真分析技術,在各領域開展了對密封結構壽命預測的研究。

SCHMIDT T等人[4]在Archard磨損模型的基礎上,運用有限元軟件的二次開發能力,計算了某O型圈的磨損量。XIN Li等人[5]采用有限元方法,對環形密封結構件進行了研究,發現隨著時間的推移,密封面體積量逐漸減小,使密封結構的密封接觸壓力先快速下降,然后趨于平穩。馮占榮等人[6]利用有限元法,對硬密封球閥密封性和應力情況進行了分析,以解決某閥門的泄漏問題。孔翔等人[7]建立了金屬密封結構的有限元模型,并通過優化結構參數,解決了密封結構的泄漏問題。常凱[8]利用Archard磨損模型及ANSYS的分析模塊,得到了模擬磨損的分析方法。張志宏[9]利用ABAQUS仿真模擬技術,對89式重機槍的身管進行了磨損研究,分析得到了子彈發射多次后,其總磨損量的計算模型。何帥旗[10]也利用ABAQUS仿真分析技術,對管線平板閘閥的閥桿動密封結構進行了磨損分析,并對密封結構的磨損壽命進行了預測。

很多學者利用有限元軟件進行了密封結構磨損規律的研究,但大多數的研究針對的是結構間全接觸磨損規律的研究,很少有研究人員對結構間磨損過程中存在不完全接觸的情況進行研究,因而對結構間不完全接觸磨損的評價方法也較少。

因此,為了滿足企業的需求,研究浮動密封結構的磨損特性,并提出合理的磨損評價方法十分必要。

綜上所述,筆者利用有限元法和磨損試驗法,對浮動密封結構進行磨損壽命預測研究;提出一種RMS作為評價浮動密封結構失效的指標,對閘板不同啟閉速度和密封面寬度與密封面的磨損量關系進行分析,以期為工程中密封結構的維護提供一定的參考。

1 閘閥密封結構

密封結構是任何一種閥門都必不可少的組成部分[11,12]。浮動密封結構是管線平板閘閥中的重要密封結構。目前,平板閘閥在各行各業中的需求量呈現逐年上升的勢頭[13]。

浮動密封結構示意圖如圖1所示。

由圖1可知:該密封結構主要包括閘板、浮動閥座、彈簧孔及密封結構的密封面。其中,z向為流體流向,y向為閘板開啟方向。

在彈簧預緊力與流體壓力的作用下,閥座向z向運動,使密封面與閘板壓緊形成密封比壓。

2 磨損基本理論與理論模型

2.1 Archard磨損理論

Archard磨損理論是研究摩擦學問題十分經典的理論[14]。Archard磨損理論描述了磨損體積與材料硬度、滑行距離和載荷的關系。其表達式如下:

(1)

式中:V為磨損體積;W為載荷;S為滑行的距離值;H為接觸中較軟物體材料硬度;k為無量綱參數。

其中:分析一般磨損問題時,k為10-8～10-4;分析嚴重磨損問題時,k為10-4～10-2。

而在80%的磨損問題研究中,對磨損深度的分析極其重要[15-17]。因此,筆者將式(1)改寫為:

(2)

式中:A為實際接觸面積;h為磨損深度。

由于壓強可表征為p=W/A,則式(2)可改寫為:

(3)

工程上,磨損量常被認為是時間上的積累量。因此,可對等式兩邊進行時間求導。速度可表示為v=dS/dt,則式(3)可改寫為:

(4)

通過積分求得磨損的深度如下:

(5)

2.2 材料的本構模型

在閘閥的啟閉過程中,浮動密封結構密封面發生磨損的原因,主要是由于流體介質壓力對密封結構產生沖擊,引發了交變載荷;密封結構的摩擦作用會使密封面產生升溫效應。

因此,筆者使用在材料熱軟化、應變以及應變率方面具有強關聯性的Johnson-Cook模型為本構方程。其表達式如下:

(6)

式中:σ為材料在加工過程中的流動應力;A為材料的屈服強度;B為材料的極限強度;c為應變敏感率;n為應變硬化指數;m為溫度敏感系數;ε0為參考應變速度;Tr為參考溫度;Tm為材料的熔點。

2.3 接觸屬性設置

接下來,筆者需要研究浮動密封結構的密封面在啟閉過程中的磨損情況。

筆者需要先定義浮動閥座和閘板零件的接觸屬性:在浮動閥座和閘板間的接觸方式方面,將法向的接觸屬性設置為“硬”接觸;而在切向方向,在平板閥門啟閉過程中,彈簧的預緊力和密封面寬度對接觸面的相互摩擦具有重要影響。

因此,根據庫侖摩擦定律對摩擦因數進行設置,其表達式如下:

(7)

式中:τf為接觸面位置的摩擦剪切壓力;σn為浮動閥座和閘板之間的正壓力;τmax為接觸面位置的最大摩擦剪切壓力;μ為摩擦因數。

2.4 材料失效準則

筆者采用剪切失效模型對工件材料失效方式進行研究。

等效塑性應變值參數D的表達式如下:

(8)

當網格單元節點上的等效塑性應變值參數D超過1時,可以判定磨損工件因失效發生分離。此處的網格單元將會被刪除[18,19]。

2.5 ALE方法

筆者采用ALE方法對有限元模型進行求解。

ALE方法大大提高了計算精度,可以確保數值仿真分析計算結果的可靠性。筆者在數值仿真分析過程中,用每一個時間步對浮動密封結構的網格進行重構;磨損的物體基于上一個時刻時的網格進行自動網格重構,避免了在磨損過程中因為網格畸變而導致計算精度下降或出現計算錯誤的情況。

ALE方法主要基于以下3個方程:

1)質量守恒方程(連續性方程)

方程如下:

(9)

2)動量守恒方程(平衡方程)

方程如下:

(10)

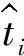
3)能量守恒方程

方程如下:

(11)

式中:E為單位質量上的能量,J/kg;qi為熱通量,J/m2。

3 基于ABAQUS的仿真分析及試驗驗證

筆者采用某公司代號Z943Y-300Lb的高壓管線平板閘閥,提取其浮動密封結構中的相關結構三維實體模型,如圖2所示。

圖2 密封結構三維實體模型圖

筆者通過試驗得到試驗數據,試驗各項參數與仿真模型一致。其中,浮動閥座、閘板的材料為F6a+WC。

零件的力學性能參數如表1所示。

表1 零件的相關參數

浮動密封結構的三維實體模型圖如圖3所示。

圖3 浮動密封結構三維實體模型圖

在圖3中,閥座密封面厚度為0.5 mm,密封面寬度為5 mm,閘板的厚度為100 mm,閘板上流體介質的最大開度為153 mm,密封接觸面的摩擦系數為0.2。

筆者根據浮動密封結構的幾何結構特點,選取浮動閥座對稱結構中5個具有代表性的區域進行磨損情況研究分析。其中,5個具有代表性的區域總節點數為43個,每個代表性區域的節點數分別為7個。

接下來,筆者針對每一個代表性區域節點的磨損特性進行研究分析。

密封面上的特征節點及其周圍節點位置如圖4所示。

圖4 節點位置示意圖

3.1 密封結構的有限元模型

為了避免不重要特征對數值模擬的影響,筆者對密封結構進行簡化處理,在滿足實際工況的前提下,對密封接觸面結構磨損進行求解。

在進行有限元網格劃分時,為了確保數值模擬結果的準確度,需將密封接觸面的網格節點對齊,對接觸位置進行局部網格細化。

筆者采用Hyper mesh軟件對密封結構進行網格劃分。密封結構的有限元模型如圖5所示。

圖5 密封結構網格模型

在進行網格劃分時,網格的總數量對密封面上節點的磨損量影響較大。為確保網格的無關性,筆者根據磨損過程中具有代表性節點N1868的磨損量和網格數量的關系,確定網格的數量。

網格無關性驗證如圖6所示。

圖6 網格無關性驗證

圖6中,可在確保仿真分析結果準確性的前提下節約運算資源,最終確定網格數量為1.2×105。

3.2 邊界條件和載荷設置

筆者對浮動閥座端面節點3個方面的自由度均施加固定約束。

浮動閥座邊界設置如圖7所示。

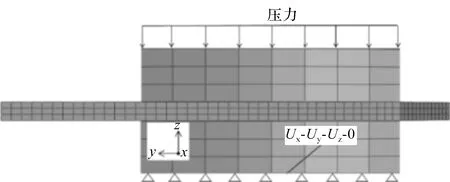
圖7 浮動閥座邊界設置

筆者在閘板x正方向上施加循環的位移載荷,單次往返的位移行程為306 mm;在閘板y方向設置固定約束,z方向自由;在流體介質的等效模型x和y方向上施加固定約束,z方向上自由,并且在z方向施加交變壓力載荷,方向為負。

閘板邊界設置如圖8所示。

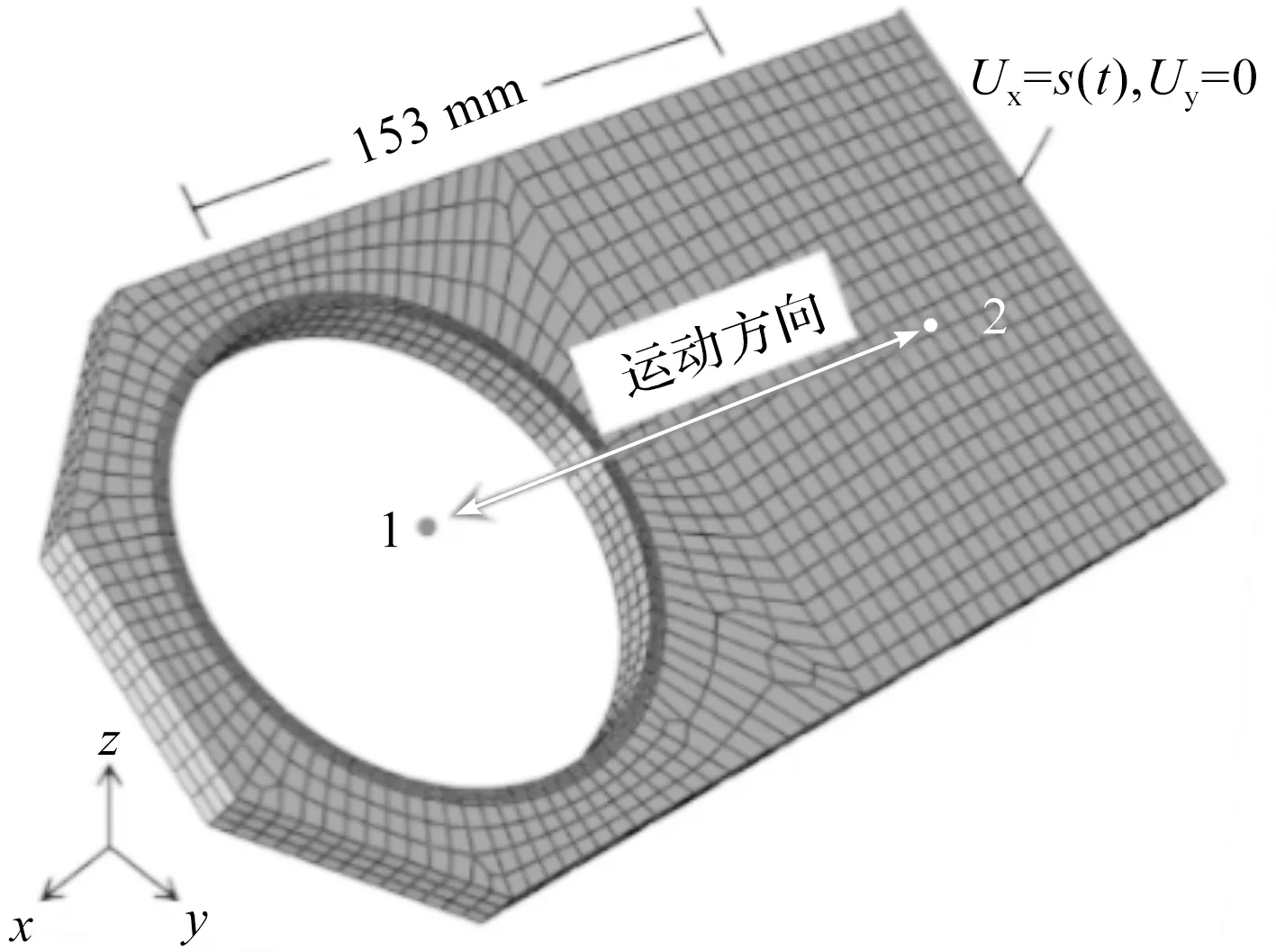
圖8 閘板邊界設置

圖8中,筆者設置閘板的邊界條件,沿著x方向為位移載荷。其中,點1到點2為閘閥開啟方向(點2到點1為關閉方向)。

p(t)表示如下:

(12)

式中:p(t)為施加在流體等效模型上在-z方向上的壓力,kN;t為運動時間,s。

3.3 仿真分析結果與試驗驗證

筆者將閘板啟閉速度和密封面寬度分別設置為153 mm/s和5 mm。

不同時刻下,密封面上特性節點的磨損情況如圖9所示。

圖9 總體磨損情況

由圖9可知:隨著浮動密封結構啟閉次數的增加,浮動閥座密封面上代表性節點(N1868～N4948)的磨損量趨于一致。而其他的代表性節點(N5498～N6708)的磨損量不相同且磨損量較小。

在浮動密封結構的磨損初期,磨損量較小,但是隨著磨損次數的不斷進行,磨損量不斷增加。浮動密封結構的RMS與浮動密封結構的啟閉次數近似呈線性關系。

磨損量評價函數如下:

(13)

式中:i為特征節點編號;Wi為在第i個特征節點處的磨損量,mm。

筆者采用仿真分析與磨損試驗結果相對比的方法,驗證磨損失效評價模型的準確性。其條件為:當RMS>0.5 mm時,密封功能失效。

代表性節點仿真分析與磨損試驗結果對比圖如圖10所示。

圖10 磨損量對比圖

由圖10可知:當啟閉速度為153 mm/s,且密封面寬度為5 mm時,浮動密封結構失效前的最大啟閉次數為1 445次;

通過磨損試驗,可測得浮動密封結構失效前的最大啟閉次數為1 396次。仿真分析和磨損試驗結果誤差僅為3.51%。

綜上所述,試驗結果不僅驗證了仿真分析模型及其結果的正確性,而且驗證了流體等效模型的合理性。

4 密封結構磨損特性分析

4.1 啟閉速度的影響

筆者采用控制變量法,將密封面寬度設置為5 mm,并分別設置閘板啟閉速度V1為102 mm/s、V2為153 mm/s、V3為306 mm/s,以探究不同啟閉速度對浮動密封結構磨損特性的影響規律。

在閘閥的不同啟閉速度下,浮動密封結構中各代表性節點的磨損量分別如圖11所示。

圖11 總體磨損情況

由圖11可知:當密封面的磨損量達到0.2 mm,閘板的啟閉速度為V1、V2和V3時,所需要的啟閉時間分別為280 s、620 s和820 s;

N1868～N5498區間內的磨損量趨于一致,且RMS隨啟閉次數的增加而增大,近似呈線性變化趨勢;N6048～N6708區間內的磨損量較小,且趨勢各不相同。

不同啟閉速度下,各區域各節點的平均磨損量如圖12所示。

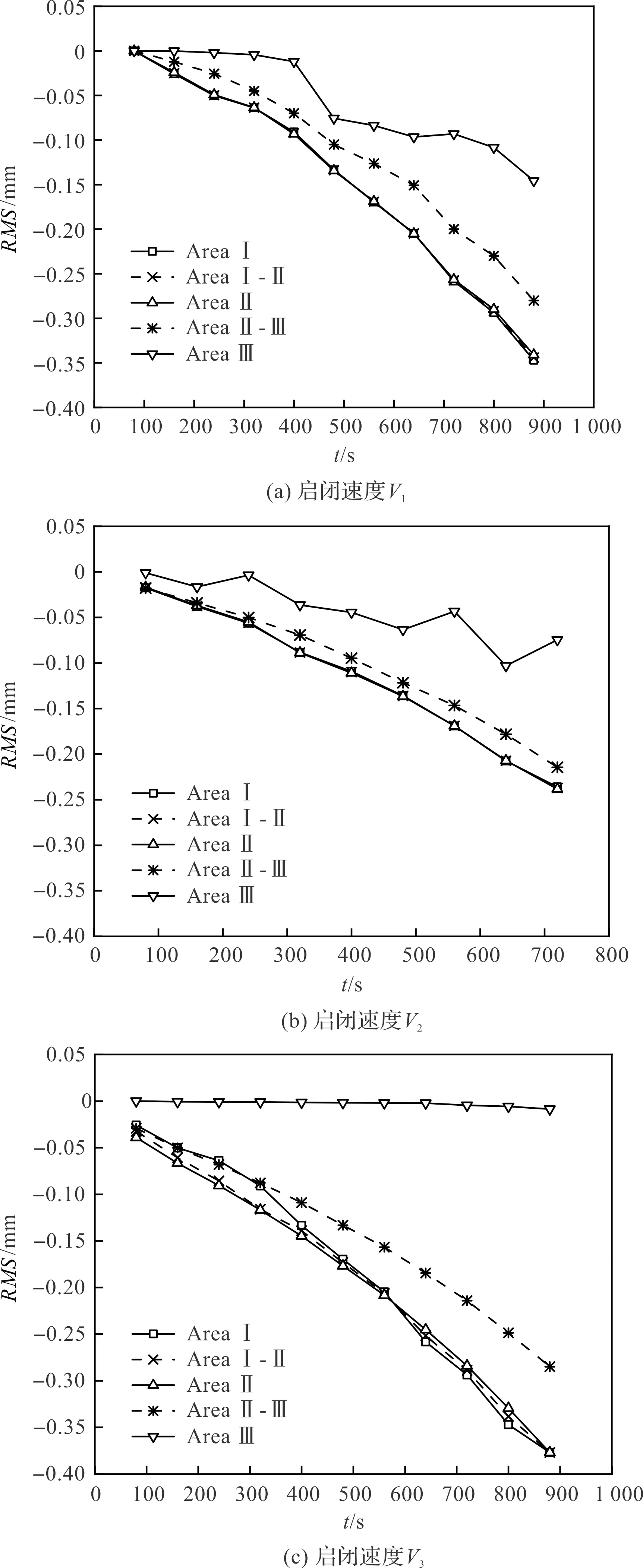
圖12 各區域平均磨損情況

由圖12(a,b)可知:啟閉速度為V1、V2時,區域Ⅰ和區域Ⅱ的磨損變化趨勢基本一致,呈近似線性變化且磨損量較大;區域Ⅲ的磨損量呈先慢后快再慢的趨勢;區域Ⅰ—Ⅱ和區域Ⅱ—Ⅲ的磨損趨勢一致,且前者較后者的磨損量更小。

由圖12(c)可知:啟閉速度為V3時,區域Ⅰ、區域Ⅰ—Ⅱ和區域Ⅱ的磨損變化趨勢基本一致。但開啟次數達到500次時,區域Ⅰ的磨損量大于區域Ⅱ;區域Ⅲ的磨損量較其他區域磨損量更小;區域Ⅱ—Ⅲ的磨損量呈快速下降趨勢,磨損量大于區域Ⅲ,且小于其他區域。

在不同啟閉速度下,典型區域的磨損輪廓圖如圖13所示。

圖13 典型區域磨損輪廓

由圖13(a～d)可知:浮動密封結構中,區域Ⅰ、區域Ⅰ—Ⅱ、區域Ⅱ和區域Ⅱ—Ⅲ在不同啟閉速度下,經過大量啟閉磨損后,最終密封面輪廓曲線不一致;其中,啟閉速度為V1、V2、V3時,其相關磨損量都依次增大。

由圖13(e)可知:在啟閉速度V1下的磨損量基本保持不變;其中,徑向距離在151 mm和156 mm時,啟閉速度V2比啟閉速度V3的磨損量小。

筆者利用最小二乘法對啟閉速度進行回歸分析,得到了不同速度下的磨損均值,如圖14所示。

圖14 磨損壽命與啟閉速度關系曲線

由圖14可知:在局部區間,隨著啟閉速度的增加,浮動密封結構的磨損壽命呈現先增加后降低的變化趨勢,且存在局部最優解。該浮動密封結構最優的啟閉速度為210 mm/s。

U(V)表示如下:

U(V)=-0.000 833·V2+0.349 7·V+4

(14)

式中:U(V)為密封結構磨損壽命,次;V為閘板啟閉速度,mm/s。

4.2 密封面寬度的影響

當啟閉速度為153 mm/s時,筆者設置密封面寬度b1為4 mm、b2為5 mm、b3為6 mm,探究不同密封面寬度對浮動密封結構磨損壽命的影響規律,并闡明密封面上不同區域的磨損機制。

在閘閥不同密封面寬度下,浮動密封結構中各代表性節點的磨損量分別如圖15所示。

由圖15(a～c)可得:N1868至N5498區間內的磨損量趨于一致,且RMS隨啟閉次數的增加而增大,呈近似線性變化趨勢;

N6048至N6708的磨損量較小,且其變化趨勢各不相同。

在不同密封面寬度下,各區域的各節點RMS如圖16所示。

圖16 各區域均方根磨損量

由圖16可知:在節點b1、b2、b3時,各區域的磨損變化趨勢基本一致,呈近似線性變化趨勢,且磨損量逐漸增加。

在節點b1和b3時,區域Ⅰ—Ⅱ、區域Ⅱ—Ⅲ和區域Ⅲ的RMS磨損變化趨勢基本一致且數值較小;然而在節點b2時,區域Ⅲ的RMS變化趨勢較為復雜。

不同密封面寬度的磨損輪廓圖如圖17所示。

圖17 典型區域磨損輪廓

由圖17可知:節點為b1、b2和b3時,磨損輪廓基本一致。當密封面磨損量值相同時,隨著密封面寬度的增加,啟閉次數也隨之增加。

筆者利用最小二乘法對3種不同密封面寬度下的磨損均值進行回歸分析,擬合結果如圖18所示。

圖18 磨損壽命與密封面寬度關系曲線

密封結構磨損壽命U′(b)表達式如下:

U′(b)=72·b2-435·b+1 802

(14)

式中:U′(b)為密封結構磨損壽命,次;b為密封面寬度,mm。

由圖18及式(14)可知:在局部區間內,隨著浮動密封結構上的密封面厚度不斷增加[20,21],浮動密封結構的磨損壽命始終呈現增大的趨勢。

5 結束語

為了解決閘閥工作過程中,因密封接觸面磨損而導致的密封失效問題,筆者采用ALE方法和Archard磨損模型,推導了浮動密封結構啟閉后的接觸面磨損厚度變化情況,運用ABAQUS軟件對其進行了摩擦動力學分析,并采用試驗測試數據對仿真結果的準確性進行了驗證。

研究結果表明:

1)浮動密封結構磨損試驗的測試結果與仿真結果吻合度在96%以上,全局磨損量均方根的評價指標較為合理;

2)浮動密封結構的密封面上區域Ⅰ和區域Ⅱ相較于其他區域的磨損量更大,這會使局部區域泄漏量過大,導致密封結構失效,因此,需要在設計或制造時重點關注該情況;

3)隨著啟閉速度的增加,浮動密封結構在局部區間上的磨損壽命呈現先增加后減小的趨勢,當啟閉速度為210 mm/s時,該密封結構磨損壽命最大;

4)浮動密封結構的磨損壽命隨著厚度的增加而增加,因此,在浮動密封結構設計時可適當增加密封面寬度。

筆者后續的研究方向是:根據浮動密封結構的磨損特性,擬采用響應面優化設計方法或拉丁超立方采樣(Latin hypercube sampling,LHS)方法,以浮動密封結構磨損壽命為優化目標,對浮動密封結構參數進行優化設計。