山地地貌地表溫度的深度學習空間模擬

鮑舒琪,張成福,馮霜,賀帥,苗林

(內蒙古農業大學 沙漠治理學院,呼和浩特 010000)

0 引言

地表溫度(land surface temperature,LST)與氣溫通過陸氣作用相互影響,氣溫變化會引起地表溫度的變化,直接影響土壤水熱過程,從而影響植被生長和枯枝落葉的分解等一系列生態過程[1]。目前主要通過遙感技術獲取大范圍地表溫度,能夠獲取實時數據,且分辨率高成本低,但不能用來預測氣候變化規律及響應[2]。李召良等[3]在地表溫度遙感反演方法研究進展中表明衛星遙感是獲取區域或全球尺度地表溫度時空分布的主要手段,但衛星傳感器只能拍攝實時數據,不能預測未來地表溫度的時空變化。

深度學習(deep learning,DL)算法具有強大的非線性映射能力與學習能力,廣泛應用于較復雜生態環境的模擬預測。Shatnawi等[4]采用非線性自回歸外生人工神經網絡模型成功模擬和預測了約旦北部2000—2016年間的地表溫度變化。蘇揚等[5]用多時相特征連接卷積神經網絡雙向重建模型(MTFC-CNN)重建軌道間隙區域的地表溫度值,其效果優于傳統的樣條空間插值和時間線性回歸方法。張義崢等[6]基于降尺度殘差網絡構建了美國密蘇里州的地表溫度深度學習模型,其降尺度效果優于經典傳統方法且穩定性更強。

下墊面的地形起伏狀況是影響地表溫度分布特征的重要因素,其復雜的自然地理環境使得地表溫度在空間與時間上存在差異性[7-8]。肖堯等[9]在復雜地表地表溫度反演研究進展中表明由于山地地貌地形起伏大、空間異質性強,出現長時序數據獲取難、地表溫度反演難等問題,導致大部分觀測站架設在平坦地區,大多數地表溫度反演算法建立在地面平坦、地形因素影響小的區域。山地地表溫度的反演需要將地形因素融入到算法,而深度學習方法能夠學習山地地形因素與地表溫度的非線性關系特征,準確模擬山地地區的地表溫度。

內蒙古大青山位于半干旱區,相對高差大,不同坡向植被分布差異較大。本文的研究目的是利用深度學習方法模擬預測該山地地表溫度的空間分布特征,并基于深度學習模型分析特定地形和植被條件下地表溫度的變化規律,以期為研究全球氣候變化對山地水熱過程和植被的影響提供一種定量的分析方法。

1 研究方法

1.1 研究區概況

內蒙古大青山位于陰山山脈中段,海拔高度在960～2 322 m之間。大青山山體呈現東西走向,北坡較平緩,有交錯分布的低山丘陵和盆地與內蒙古高原相連,南坡陡峭,為剝蝕堆積形成的構造斷裂地形[10]。大青山位于溫帶大陸性半干旱季風氣候區,區內有山地森林、灌叢和草原植被,是土默川平原及黃河上中游地區重要的水源補給區。

1.2 數據來源與預處理

數據包括ASTER DEM 30 m高程數據、2019—2021年5—9月生長季的MODIS產品數據(表1)和氣象數據。經輻射定標和大氣校正等預處理的MOD09A1、MOD11A2、MOD13A1產品數據來源于NASA網站(https://ladsweb.modaps.eosdis.nasa.gov/)。ASTER GDEM 30 m高程數據來源于地理空間數據云(http://www.gscloud.cn/)。氣象數據來源于中國氣象數據網(http://data.cma.cn/)的6個氣象站點的氣候資料數據集。

表1 MODIS產品計算公式

用NASA提供的MRT(MODIS Reprojection Tool)軟件對MODIS數據進行分層處理,提取LST、歸一化植被指數(normalized difference vegetation index,NDVI)、地表反照率等數據,用ENVI、ArcGIS軟件進行計算、重投影、格式轉換及圖像鑲嵌裁剪。

用ArcGIS軟件的空間分析工具基于高程數據計算海拔、坡度、坡向等地形因子數據。用ArcGIS軟件的反距離插值法將6個氣象站點數據插值為與研究區像元大小一致的空間柵格圖像,與研究區環境因子的各像元相對應。用ArcGIS軟件的投影變換功能將所有空間數據統一坐標系為WGS 1984 UTM、空間分辨率為500 m。

1.3 地表溫度的環境因子重要度分析

選擇影響LST的環境因子構建模型時,為防止數據集中存在大量冗余數據增加算法的成本,避免過度擬合,使用特征選擇算法挑選與目標變量高度相關的特征變量,能有效提高算法的性能[11-12]。本文在構建LST模型之前,運用決策樹(decision tree,DT)構造算法中的分類回歸樹(classification and regression tree,CART)[13],對可能引起LST變化的環境因子(如氣溫、海拔、植被蓋度等)進行特征重要度分析,選取特征貢獻度較大的因子進行LST模型構建。

1.4 深度學習模型的構建

1)深度學習方法介紹。深度學習本質是利用多層的非線性信息處理來進行監督或無監督的特征提取和轉換,并進行模式分析和分類,可以通過多層學習訓練獲得更高層的特征信息[14]。深度學習神經網絡由輸入層、一個或多個隱藏層、輸出層和每層中的神經元組成,每個神經元有一個權值和偏置對應上一層的神經元,輸入層神經元數量為輸入特征變量的數量,輸出層的神經元數量為訓練過程中給予神經網絡的輸出數量,隱藏層神經元數量和隱藏層數量的正確選擇取決于輸入輸出關系的復雜程度[15]。

2)LST模型構建。本研究在數據科學管理軟件Anaconda的Jupyter notebook平臺,利用以Tensorflow 2.0為后端的深度學習庫Keras進行模型的構建運行與測試。

從環境因子(如氣溫、海拔、NDVI等)和LST的空間柵格圖像上隨機選取1 200個樣本點,提取2019—2021年3年數據共3 600個樣本作為模型數據集。以決策樹模型選取的環境因子作為輸入層數據集,LST作為輸出層數據集建立深度學習模型。輸入層數據集的70%劃分為訓練集,20%劃分為測試集,10%劃分為預測集。模型的激活函數設置為Relu,優化器選取RMSprop。經多次訓練后,確定藏層、神經元個數和迭代次數,構建最優LST模型。

3)模型評估。用回歸損失函數均方誤差(mean squared error,MSE)和平均絕對誤差(mean absolute error,MAE)評估模型預測值與真實值之間的差距,衡量模型模擬性能和預測精度。MSE用來評價數據的變化程度,MSE值越小說明模型預測具有更好的精確度,MAE可以準確反映實際預測誤差情況。

4)單個因子對LST空間變化的分析。在已構建的深度學習模型基礎上,將待分析的單個環境因子設置為若干等級,同時將其他環境因子固定為區域均值(表2),以此計算LST隨這一因子的變化規律。

表2 各環境因子均值表

研究區NDVI空間范圍在0.14～0.91,等級間距設置為0.05;日均氣溫空間值范圍在14.18～20.57 ℃,等級間距設置為0.25 ℃;海拔空間范圍在960～2 322 m,等級間距設置為50 m;地表反照率空間范圍在0.06～0.21,等級間距設置為0.01;坡度空間范圍在0°～66.5°,等級間距設置為5°。

5)不同植被覆蓋情景下LST空間變化對于單個因子的響應。為分析各環境因子在不同植被覆蓋度下對LST分布的影響,本文根據《土壤侵蝕分級標準》中的植被覆蓋度分級標準,設定4種NDVI情景模式:NDVI為0.2(低植被覆蓋)、0.4(中低植被覆蓋)、0.5(中等植被覆蓋)和0.8(高植被覆蓋)。基于構建的LST深度學習模型,分析在不同植被覆蓋情景下,LST隨各個影響因子的變化規律,同樣設置其他特征變量為均值(表2)。

2 結果與分析

2.1 環境因子重要度分析

選取對LST空間分布變化有影響的7個環境因子(平均氣溫、高程、坡度、坡向、剖面曲率、NDVI和地表反射率),經決策樹模型篩選出相對貢獻率較高的因子為平均氣溫、坡度、地表反照率、海拔和NDVI(貢獻率分別為0.008、0.087、0.09、0.227、0.588),相對貢獻率較低的因子為剖面曲率和坡向因子(貢獻率均為0)。環境因子重要度見圖1。

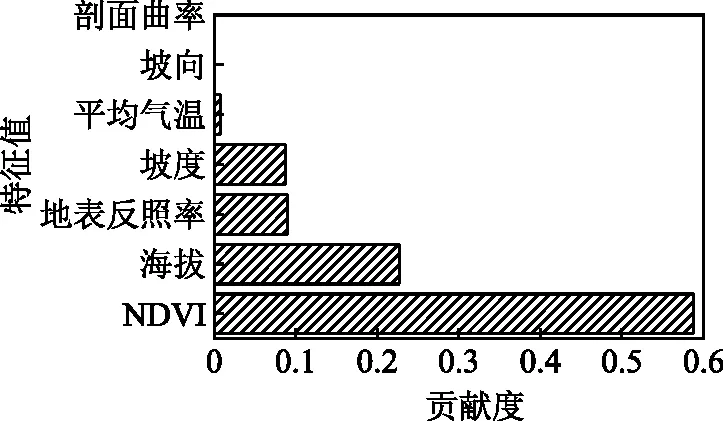
圖1 地表溫度空間分布的環境因子貢獻度

2.2 深度學習模型預測精度

圖2為模型預測模擬的LST值與觀測值對比圖。預測結果表明模型精度最高(MAE為0.60 ℃,MSE為0.65 ℃)的隱藏層個數為3層,訓練迭代次數為30 000次。圖2(a)表明預測值與觀測值對比較吻合,構建的深度學習模型能很好地預測模擬LST的變化趨勢,預測值與觀測值的變化波動規律一致,模型預測結果較準確。由圖2(b)可知深度學習模型預測的LST值與LST觀測值散點分布較集中,比較貼合在相關線附近,且散點圖決定系數R2為0.89,說明深度學習構建的LST模型預測模擬效果較好,擬合效果較優,擬合穩定性較高。因此使用深度學習方法對LST進行模擬具有一定的可靠性。

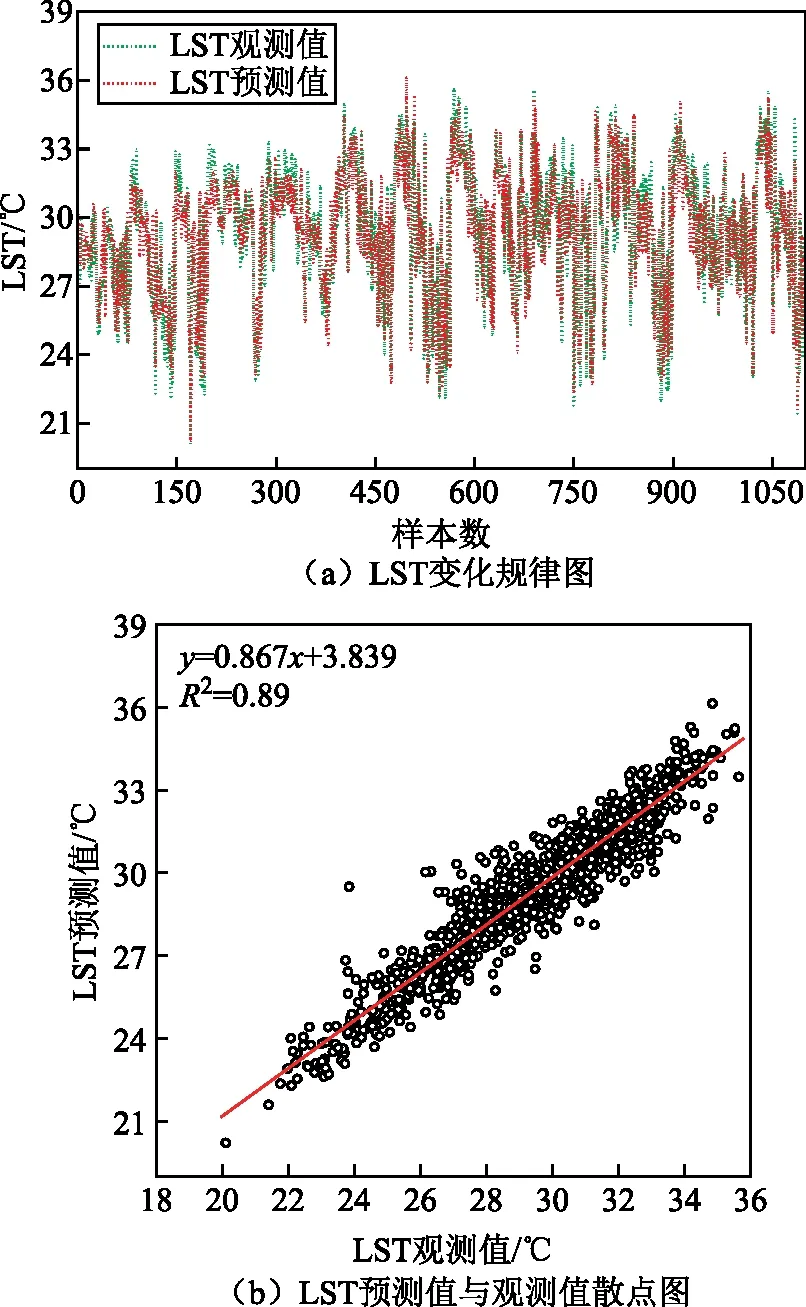
圖2 模型預測模擬的地表溫度值與觀測值對比圖

2.3 地表溫度空間分布的模型預測分析

圖3是2021年LST的觀測值與預測值空間分布圖。對比發現觀測值與預測值的空間分布特征相近,每段LST區間分布區域都較為吻合,且地表溫度最低值僅相差0.32 ℃,最高值僅相差0.83 ℃,模擬值比觀測值空間分布較清晰。研究區西部、北部和南部地帶LST最高(30.5～37.36 ℃),因其位于大青山山腳,海拔相對較低且植被覆蓋較小(NDVI低于0.5);中部區域LST最低(20.38～28.5 ℃),因其是呼和浩特大青山主要山體部分,海拔高且植被覆蓋大(NDVI達0.7);由于其余地帶海拔介于上述兩個地帶之間,LST為28.5～30.5 ℃。

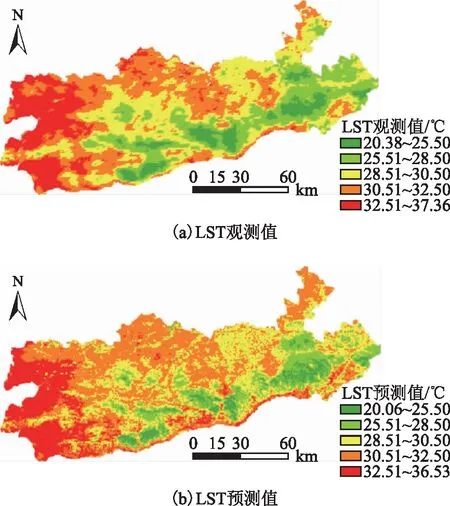
圖3 地表溫度預測值與觀測值的空間分布對比圖

2.4 單一控制變量下LST隨環境因子的變化分析

NDVI與LST的決定系數R2為0.95;隨NDVI增加LST呈下降趨勢,NDVI每增加0.1時LST降低1.41 ℃(圖4(a))。平均氣溫與LST的決定系數R2為0.86;隨平均氣溫的增加LST呈上升趨勢,平均氣溫每增加1 ℃時LST上升0.33 ℃(圖4(b))。海拔與LST的決定系數R2為0.85;隨海拔高度的增加LST呈下降趨勢,海拔高度每增加50 m時LST減小0.18 ℃(圖4(c)),在海拔1 600 m以上的LST下降速率較大。坡度與LST的決定系數R2為0.61;隨坡度的增大LST整體呈下降趨勢,坡度每增加1°時LST下降0.23 ℃(圖4(d)),在45°以下坡度的LST下降速率較小,在45°以上坡度的LST下降速率較大。地表反照率與LST的決定系數R2為0.88;隨地表反照率的增加LST呈上升趨勢,地表反照率每增加0.01時LST升高0.02 ℃(圖4(e))。

圖4 地表溫度隨單一控制變量變化的規律圖

2.5 不同植被覆蓋情景下LST隨影響因素的變化分析

圖5是4種NDVI情景下模擬LST隨單一環境因子的變化規律,表3是圖5中每個線性曲線的函數參數信息表。圖5(a)是在4種NDVI的情景下模擬LST隨平均氣溫(14.5～20.5 ℃)單一變量下的變化情況。隨NDVI增加,LST隨平均氣溫上升而增加的增速呈下降趨勢。當NDVI為0.2時,LST增加速率為0.52 ℃/℃;NDVI為0.4和0.5時,LST增加速率分別為0.09 ℃/℃和0.31 ℃/℃;NDVI為0.8時,LST增加速率為0.04 ℃/℃(圖5(a)、表3)。在NDVI為0.2情景下,LST受平均氣溫影響較其他情景模式明顯,隨著平均氣溫的增加,LST在32.53～35.38 ℃之間逐漸升高,而在NDVI為0.4和0.5兩種情景模式下,LST受平均氣溫影響差異性較小。

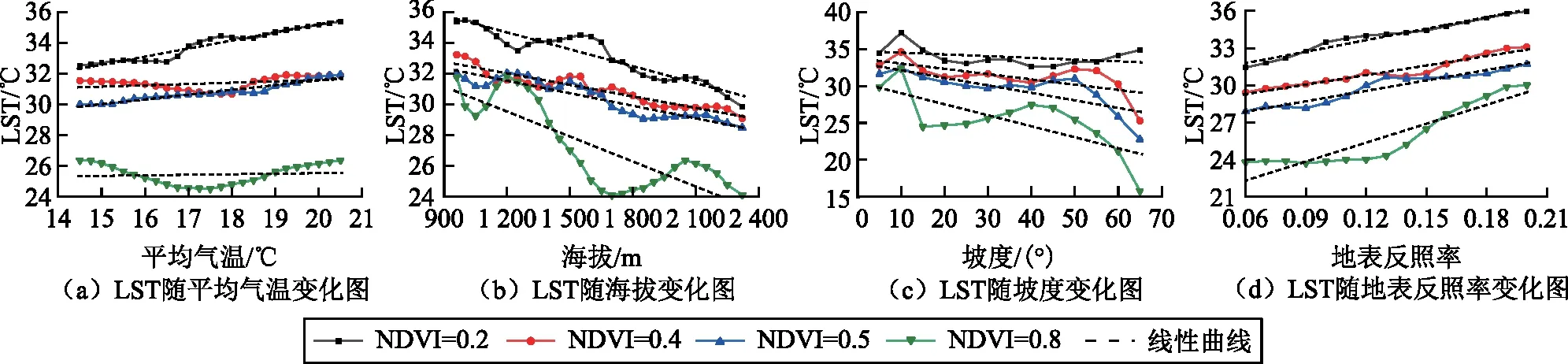
圖5 地表溫度在不同植被覆蓋情景下隨平均氣溫、海拔、坡度、地表反照率的變化規律圖

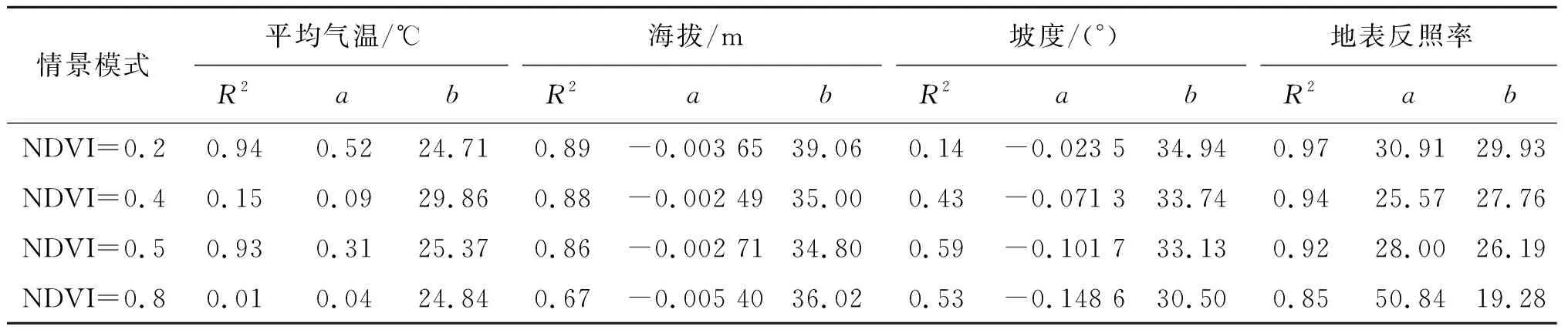
表3 地表溫度在不同植被覆蓋情景下隨平均氣溫、海拔、坡度、地表反照率變化的線性函數參數表

圖5(b)是在4種NDVI情景下模擬LST隨海拔(960～2 322 m)單一變量下的變化情況。隨NDVI增加,LST隨海拔增大而下降的降速呈先下降后增大趨勢。NDVI為0.2時,LST下降速率為0.18 ℃/50 m;NDVI為0.4和0.5時,LST下降速率分別為0.12 ℃/50 m和0.14 ℃/50 m;NDVI為0.8時,LST下降速率為0.27 ℃/50 m;在海拔1 200 m高度出現最大值31.87 ℃,在1 500 m以上高度LST下降至最低,這是因為在研究區海拔較低處是比較平坦的城郊山腳地區,地表植被覆蓋較小,地表吸收的太陽輻射能量較多,地表溫度較大,在研究區海拔較高處則是大青山山體部分,植被覆蓋度較大,地表吸收的太陽輻射能量就越少,使地表溫度越低。

圖5(c)是4種NDVI情景下模擬LST隨坡度(0°～65°)單一變量下的變化情況。隨NDVI增加,LST隨坡度增大而下降的降速呈增大趨勢。當NDVI為0.2時,LST下降速率為0.02 ℃/(°);NDVI為0.4和0.5時,LST下降速率分別為0.07 ℃/(°)和0.10 ℃/(°);NDVI為0.8時,LST下降速率為0.15 ℃/(°)。

圖5(d)是4種NDVI情景下模擬LST隨地表反照率(0.06～0.21)單一變量下的變化情況。隨NDVI增加,LST隨地表反照率增大而增加的增速呈先下降后增大趨勢。NDVI為0.2時,每增加0.1地表反照率LST增加0.31 ℃;NDVI為0.4和0.5時,每增加0.1地表反照率LST分別增加0.26 ℃和0.28 ℃;NDVI為0.8時,每增加0.1地表反照率LST增加0.51 ℃。

3 討論

3.1 深度學習方法對山地地表溫度空間分布的模擬精度

本研究使用深度學習方法模擬了內蒙古大青山地表溫度的空間分布,得到了很好的模擬結果,表明該方法模擬復雜地貌下地表溫度空間分布具有可行性。本研究使用決策樹算法對環境因子進行特征重要度分析。與汪子豪等[16]基于BP神經網模擬地表溫度時不對輸入層數據進行篩選的研究結果(RMSE為0.98 ℃)相比,使用決策樹算法減少了輸入變量的數據冗余,提高了模擬精度。使用深度學習方法構建LST模型時,需要選擇合理的輸入因子、適當的隱藏層節點數以及訓練次數才能獲得較高的模型精度[17]。

基于深度學習對地表溫度的模型構建多在地形平坦區域研究[18-19],而在高山地區由于其復雜的地形情況,利用深度學習是否能準確估算模擬高山地區的地表溫度的研究較少。

3.2 環境因子與山地地表溫度的關系

地表溫度的時空分布特征受氣象溫度、植被覆蓋和地形地貌等多個環境因素的共同影響,且這些環境因素之間也相互作用,使得地表溫度在區域尺度上的時空分布狀況具有一定的復雜性和差異性[20]。研究區東南部海拔高、坡度陡、植被覆蓋度高共同導致地表溫度最低;北部和西部區域海拔低、坡度平緩、植被覆蓋度低共同導致其地表溫度較高。在以往的研究中更多的是簡單分析了地表溫度與環境因子的相關性特征[21-22],未考慮到其他環境因素的潛在影響,而本文在分析地表溫度隨某一環境因子的變化規律時,利用深度學習方法控制其他環境因子為均值,使結果更具有準確性。

本研究發現,影響大青山地表溫度的主要環境因子有NDVI、海拔、地表反照率、坡度和氣象站平均氣溫,其中影響最大的因子是NDVI,其次是海拔和坡度,而坡向影響最小,這與羅瑤等[23]的研究結果一致。NDVI是地表溫度影響最大的環境因子,LST隨NDVI的增大而降低,是由于植物可以吸收和轉化太陽輻射從而降低地表溫度[24]。本研究中LST隨地表反照率的增大而升高,表明地表反照率在15%～28%之間時,地表溫度隨反照率的增大而升高;地表反照率大于40%時,地表溫度隨反照率的增大而減小[25],本文由于大青山的地表反照率范圍在0.06～0.21之間,地表反照率非常小,所以僅出現了地表溫度隨地表反照率增大而升高的情況。在大青山復雜的地貌環境條件下,其特殊的地形因子(海拔、坡度、坡向等)也是影響地表溫度的重要環境因子,在地表溫度的空間分布特征中有著直接或間接影響。不同地形因子對地表溫度的影響存在差異,大青山海拔與地表溫度的關系不是簡單的線性關系,LST隨海拔的增大而降低,在海拔1 600 m以上LST下降明顯。這是由于在對流層海拔越高大氣吸收的地表長波輻射能量越少,大氣儲存的熱量越低氣溫就越低,從而影響地表與空氣之間的熱交換[26]。坡度與坡向主要因其不同坡度坡向條件下坡面吸收的太陽光照的大小不同,從而影響坡面LST的大小[27]。LST隨坡度的增大而降低,在0°～45°時LST下降速度較小,在45°以上時LST下降速度顯著。造成這種現象的原因是不同坡度的太陽入射強度和反射率不同,導致地表吸收的能量不同,由于險坡吸收的太陽輻射較小,導致LST較小。本研究發現,坡向因子與LST之間的關系不明顯,這可能與本研究使用的MODIS數據分辨率較大不能夠反映當地坡向變化有關。今后在使用深度學習方法模擬山地空間溫度變化時,應考慮選擇空間分辨率更高的數據。

地表溫度受下墊面及氣候環境中多種因素的共同影響,是多種因子相互作用的結果,本文由于數據的獲取難度以及研究水平的局限性僅選取了部分因子進行訓練,但在選擇影響因子進行模型訓練過程時是否還有更多的有效因子還未被驗證,在后續研究中將充分考慮多種環境因子進行模型的構建。

4 結束語

本文基于環境因子數據集利用深度學習算法模擬預測了大青山LST的空間分布,并分析單一環境因子和植被變化情景下各環境因子與LST的關系,得到如下結論。

1)通過決策樹模型運算發現,植被覆蓋NDVI對LST的貢獻度最大(0.588),其次是海拔(0.227)、坡度(0.087)、地表反照率(0.09)和平均氣溫(0.008),最低的是剖面曲率(0)和坡向(0)因子。

2)利用深度學習神經網絡構建的LST模型精度MAE達0.60 ℃,MSE達0.65 ℃;預測模擬的決定系數R2達0.89。

3)LST隨NDVI的增加而降低,NDVI每增加0.1時LST下降0.41 ℃;LST隨平均氣溫增加而升高,增加速率為0.33 ℃/℃;LST隨海拔升高而降低,下降速率為0.18 ℃/50 m;LST隨坡度增大而降低,下降速率為0.23 ℃/(°);LST隨地表反照率增大而增加,地表反照率每增加0.01時LST升高0.31 ℃。

4)隨NDVI的增大,LST隨平均氣溫上升而升高的速率呈下降趨勢,隨海拔升高而下降的速率呈先減小后增大的趨勢,隨坡度增加而下降的速率呈增大趨勢,隨地表反照率增大而升高的速率呈先減小后增大的趨勢。