基于遺傳算法的垃圾轉運集裝箱密封條優化設計

周志勇, 沈海紅, 黃長纓, 郭玉文, 張 歐, 蔡永華

(1.現代汽車零部件技術湖北省重點實驗室,湖北 武漢 430070; 2.汽車零部件技術湖北省協同創新中心,湖北 武漢 430070; 3.武漢理工大學 汽車工程學院,湖北 武漢 430070; 4.上海環境物流有限公司,上海 201900)

0 引 言

隨著中國城市化進程加速,各大城市正面臨著垃圾量增加、垃圾中轉站收運壓力大、垃圾收運處理成本高等問題,合理解決垃圾轉運問題已成為城市工作的一個重點[1-2]。上海市垃圾轉運主要應用聯運式專用集裝箱進行,由于集裝箱密封條自身結構的限制以及各種復雜工況和反復開關門的影響,密封條使用一段時間后會存在永久變形,集裝箱工作時存在滲漏現象。因此,必須首先應用RT2000慣導對箱體移動軌跡和運行工況進行追蹤記錄和分析,以便分析密封條受力情況;然后測量箱體和密封條的尺寸,并進行模擬分析。

國內外已有學者對密封條結構形狀優化設計展開研究。文獻[3]針對汽車尾門處的漏水問題,應用ANSYS分析軟件,對尾門密封條展開研究,并對尾門密封條形狀進行優化,為解決尾門漏水問題提供可行的方法;文獻[4]針對傳統密封系統結構簡單、局部受力大等問題,通過研究密封過程的性能要求,提出一種變截面密封條優化設計的方法以滿足車門密封中各種性能要求;文獻[5-6]利用ANSYS軟件對密封條進行結構分析,通過密封條應力變形分析,對密封條的結構尺寸進行重新設計,使密封條的壓縮負荷滿足設計目標要求;文獻[7]針對傳統有限元分析難以對多參數問題同時優化,提出聯合多軟件的多目標優化方法,通過仿真分析,對密封條進行優化設計,并得到壓縮負荷與接觸寬度最優的密封條結構;文獻[8]研究了密封橡膠薄膜的應力狀態,并對薄膜的各參數進行了計算求解。

針對密封條結構優化設計,很多學者開展了有限元仿真分析研究,但是,聯合神經網絡遺傳算法對其進行優化研究相對較少。文獻[9]針對液膜密封直接測試較難實現的問題,提出基于BP神經網絡的性能監測方法,利用實驗數據訓練BP神經網絡得到最優BP神經網絡模型;文獻[10]針對傳統測試方法對密封端面識別準確率較低、識別速度慢的問題,提出了一種基于遺傳算法改進的密封狀態進行識別的方法。

本文基于上海市虎林路碼頭濕垃圾聯運式專用集裝箱用密封條進行研究。首先應用分析軟件對原密封條應力狀況展開研究,然后應用神經網絡遺傳算法對密封條展開優化設計,最后分析對比優化密封條的各項性能,擬有效解決集裝箱滲漏問題。

1 優化算法及結構仿真

1.1 原密封條結構分析

原集裝箱密封條其截面為上部呈山峰狀,中間開有一個24 mm×16 mm(長×寬)矩形槽,兩側有倒刺形狀的凸起,倒刺為邊長4 mm的正三角形,共10 個倒刺,原密封條分析圖如圖1所示。該密封條的總寬度為40 mm,總高度為54 mm,上層部分的最低端距離矩形槽的頂端為10 mm。

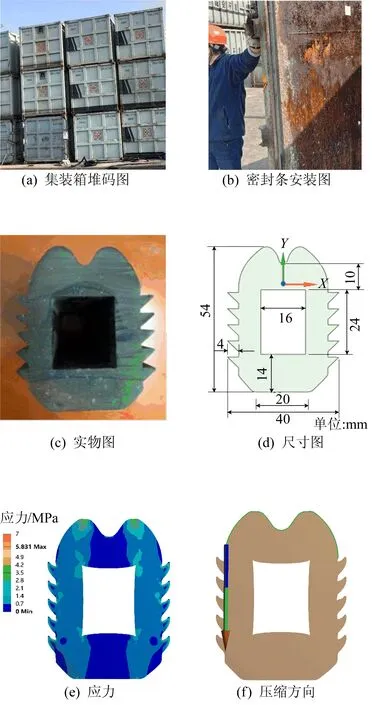
圖1 原密封條分析圖

所研究轉運集裝箱的腔內高度為2 m,轉運垃圾量約為17 t,轉運垃圾裝載高度為1.7～1.8 m,濕垃圾比重約為0.8。垃圾轉運集裝箱為水平式橫關門,考慮到垃圾轉運集裝箱在轉運過程中存在傾斜、慣性力等作用,取1.5的安全系數,此時箱門受力約為38.10 kN。根據CJ/T 496—2016《垃圾專用集裝箱》中7.6.3多式聯運垃圾專用集裝箱的密封性要求,箱門所受平均壓強為箱門受力上下端壓強的平均值,此時箱門受力約為38.22 kN,平均壓強約為0.105 MPa。故取受力較大值38.22 kN為箱門密封合緊力設計標準。

應用ANSYS分析軟件,對原密封條進行仿真模擬實驗。選擇原密封條為三元乙丙材料,并設置4對接觸對,選擇位移壓縮,壓縮量為8 mm,門與箱體間隙為11 mm,對密封條進行關門測試仿真,并得到仿真結果。由圖1可知,壓縮力為22 240 N時,最大應力為5.83 MPa;接觸力為22 240 N時,接觸應力為1.00 MPa,接觸長度為29.1 mm。

考慮到密封條的使用壽命,密封條壓縮后內部最大應力應當盡可能小;為應對門框上可能存在的異物,密封條與門框的接觸長度應當盡可能長,以便包裹住異物。

1.2 BP神經網絡算法

BP神經網絡包含輸入層、隱含層、輸出層3層,是一種誤差反向傳播、信號向前傳遞的多層前饋神經網絡。前向傳遞信號時,由輸入層經隱含層處理,最后至輸出層,得出神經網絡[11-13]。訓練步驟如下:① 初始化;② 隱含層輸出;③ 輸出層計算;④ 誤差分析;⑤ 權值更新;⑥ 判斷算法是否結束,否則返回步驟②。

1.3 遺傳算法

遺傳算法(genetic algorithm,GA)是通過自動獲取和積累有關信息,自適應控制搜索過程并求得最佳解,是一種高效的方法,起源于對生物模擬研究[14-16]。主要步驟如下:① 初始化;② 計算個體的適應度;③ 按適應度值所決定的規則選擇下一代個體;④ 交叉操作;⑤ 變異操作;⑥ 滿足停止條件,輸出結果,否則轉入步驟②。

1.4 材料模型

為計算求解方便,在對超彈性材料的應力應變分析中,采用Mooney-Rivlin模型描述超彈性材料的特性。本文采用應變能密度函數W表征超彈性材料的特性,對其求應變分量的一階導數[17],即

(1)

其中:S為第二類Piola-Koshy Hoff應力張量;W為應變能函數;E為Lagrange應變張量。應變能函數W表示為:

W=(I1,I2,I3)

(2)

其中,I1、I2、I3為應變不變分量。

(3)

其中,Cij為常數,且滿足C00=0。應變不變量I1、I2、I3為:

(4)

其中:J為體積比;λi為主拉伸率,與應變εi的關系為:

λi=1+εi

(5)

聚脂橡膠TPEE具有不可壓縮性,當其在受到外載荷時體積不變,受力前后的體積比為 1∶1,即J=1。式(4)可以簡化為:

(6)

應變能函數W可以表示為:

W=C10(I1-3)+C01(I2-3)

(7)

其中:I1、I2為應變張量的主不變量;C10、C01為Mooney-Rivlin材料常數。式(7)是在工程中廣泛應用的Mooney-Rivlin材料模型,可以用來描述絕大多數超彈性材料的力學特性。根據式(5)、式(6),可推導出TPEE材料的主應力σi和主伸長率λi之間的關系為:

(8)

對TPEE材料試片進行單軸拉伸實驗,由于是單向拉伸,另外2個方向的主應力均為0,即

σ2=σ3=0

(9)

TPEE材料具有不可壓縮性,因此有:

(10)

則式(8)可變形為:

(11)

根據式(7),可得:

(12)

由式(11)、式(12)可得:

(13)

取

(14)

則式(13)可以簡化為:

Y=C10+C01X

(15)

根據單軸拉伸實驗,可得出TPEE材料試片變形和所受載荷的變化關系,由該變化關系計算出一系列拉伸率λ1和與其對應的應力σ1的值,再根據拉伸率和對應的應力值計算出式(15)中的X和Y,將所有X和Y通過MATLAB軟件擬合成一條直線,則C10為該直線的截距,C01為該直線的斜率,因此可對密封條的材料屬性進行設置。

2 密封截面結構參數優化

2.1 密封條截面優化

本文目標是在保證接觸力足夠的情況下,通過對密封條的結構形狀進行優化來降低密封條的接觸應力,增加密封條的接觸長度,密封條的結構形狀優化可通過優化密封條的形狀、高度、寬度等參數來進行實現,經過優化分析,確定最合理的設計方案[18]。密封條結構優化問題可描述為:

minF(X)

(16)

X={x1,x2,…,xn}

(17)

s.t.Ri(X)≤0,i=1,2,…,n

(18)

aj≤xj≤bj,j=1,2,…,n

(19)

其中:F(X)為目標函數;Ri(X)為約束函數;ai、bj分別為設計變量的上、下限。

根據對密封條仿真受力變形的分析,并結合工程實際經驗,選取密封截面結構形狀編號m、寬度t、高度T3個變量為優化參數。對于相同材料制成的密封條,在壓縮量相同的情況下,壓縮負荷F和應力σ是截面形狀編號m、厚度t、高度T的函數,即F=f1(m,t,T),σ=f2(m,t,T)。利用加權和的辦法,可將此多目標問題轉化為一個單目標優化問題,構造如下目標函數:

g=λ1F+λ2σ

(20)

其中,λ1、λ2為權值。根據密封條實際運行工況進行分析,考慮到F與σ的相對大小及相互重要性,分別取λ1=0.3、λ2=0.7,此比例最能反映密封條性能[19]。因此,密封條的結構優化問題轉化為對參數k、t、T進行優化,得出目標函數g的最小值。

通過仿真模擬計算和分析,取5種性能相對較好的截面形狀密封條進行研究優化,截面圖如圖2所示。

圖2 密封條截面形狀

由于密封條截面薄厚不均,且相對復雜,各變量取值范圍的界定變得困難。結合工程設計經驗歸納總結出各變量取值范圍,具體的變量類型與取值范圍見表1所列。

表1 截面優化變量

為避免全排列數據量大,計算復雜,消耗時間長,因此采用正交設計法進行設計。m、t、T取5組數據,可采用L25(53)水平法來進行計算分析,然后通過有限元分析法計算數據F和σ,結果見表2所列。

2.2 神經網絡訓練、基于遺傳算法截面優化結果

本研究利用3層BP神經網絡進行計算和分析,其中輸入神經元數取3,分別對應m、t、T。根據神經網絡的結構近似分析方法原理[20],取隱層神經元數為5,輸出神經元數為2,結構如圖3a所示。神經網絡輸出結果如圖3b可知,由圖3b可知,此神經網絡基本實現了所要逼近的非線性函數的功能。

圖3 神經網絡與遺傳算法

通過遺傳算法進行優勝劣汰的結構參數優化篩選運算。本文取群體大小為30、交叉率Pc為0.4、變異率Pm為0.2。經過多代進化,得到優化結果m=3、t=4.4 mm、T=64 mm,此時,F=8 125 N、σ=0.28 MPa,采用有限元軟件對優化結果進行對應設計參數的計算,計算結果為F=7 712 N、σ=0.32 MPa,相對誤差分別為5.1%、14.0%。進化迭代曲線如圖3c所示。

2.3 性能對比

優化前后密封條各參數對比如圖4所示。原密封條最大應力為5.83 MPa,等壓縮量時的壓縮力為22 240 N。

圖4 優化前后密封條各參數對比

由圖4可知,優化后密封條最大內應力為3.53 MPa,相比優化前降低39.4%,等壓縮量時的壓縮力為7 712 N,相比優化前降低65.3%,且接觸長度增加18.6 mm,密封壓力0.18 MPa。

3 裝車實驗

3.1 壓力驗證

為了驗證有限元分析的準確性和有效性,對密封條實際裝車關門后的密封壓力進行測量,采用型號為LLW與LW的富士壓敏紙進行測試。將密封條劃分為18段區域采集。壓敏紙安裝及測量結果示意圖如圖5所示。

圖5 壓敏試紙安裝及測量結果示意圖

通過色卡對比,密封條水平段的實測壓力為0.188 MPa,與上述有限元分析的密封壓力0.180 MPa基本一致,也高于設計安全壓力0.105 MPa。

3.2 密封性實驗

研究組首先進行了密封條的水密性實驗。對集裝箱進行了注水實驗,將水注入集裝箱內并達到集裝箱的2/3高度,此時實驗裝載質量約為23.22 t(正常運行裝載質量約為18 t),靜置72 h后無滲漏,且密封條無明顯的擠壓變形,水密性實驗如圖6a所示。隨后進行垃圾裝車實驗,裝載4車濕垃圾加1車餐廚垃圾,放置24 h后無滲濾液出現。優化后的密封條裝車實驗表現較好,裝車實驗如圖6b所示。

圖6 密封性實驗

4 結 論

本文針對垃圾轉運集裝箱存在滲漏的情況,對密封條進行了有限元分析,通過神經網絡遺傳算法對密封條的結構形狀進行優化,并進行裝車實驗驗證,主要結論如下:

1) 通過優化設計密封條的幾何特征和尺寸,能解決集裝箱存在滲漏的情況。

2) 形狀3在壁厚為4.4 mm、高度為64 mm時,壓縮負荷和應力都能達到目標函數要求。

3) 優化后密封條的最大內應力降低39.4%。

4) 優化后密封條等壓縮量的壓縮力降低65.3%。