蠟燭火焰耦合振蕩的研究

方 蓮, 宋家樂, 王雅萍, 潘 剛, 蘇一恒, 林彤彤

(1.合肥工業大學 基礎部,安徽 宣城 242000; 2.合肥工業大學 土木與水利工程學院,安徽 合肥 230009; 3.合肥工業大學 計算機與信息學院,安徽 合肥 230601)

0 引 言

彼此鄰近的蠟燭燃燒時能觀察到振蕩的火焰,這種振蕩可以相互耦合,產生豐富的動力學行為。20世紀40年代至今已有多篇文獻對蠟燭火焰的振蕩與不穩定性、蠟燭間距不同對應的2種同步模式、拓樸結構耦合系統的振蕩模式、同相與反相同步振幅衰減和相位差、蠟燭火焰的頻率和相位特性等內容進行探討[1-9],但在影響蠟燭耦合振蕩因素上的結論仍存在一定的爭議,需要進一步研究討論。

本文在已有研究的基礎上,探討不同直徑的2組全同蠟燭火焰之間的耦合振蕩情況,得出2組全同蠟燭同相和反相振蕩與距離的關系、振蕩頻率與蠟燭組間距之間的關系、蠟燭組直徑不同對耦合范圍的影響,并結合實驗仿真情況討論熱輻射、熱對流在耦合中的作用,明確了熱對流是蠟燭耦合振蕩的主導因素,并從渦動力學角度對耦合振蕩機理給出解釋。

1 理論分析

2組蠟燭火焰之間有3種可能的傳熱形式,即熱擴散、熱對流和熱輻射,其中熱擴散的影響微弱[3],因此考慮蠟燭火焰振蕩主要是熱對流和熱輻射共同作用的結果。

根據能量守恒和氧平衡方程,對于單組蠟燭火焰振蕩,其振蕩過程的方程表達如下:

(1)

(2)

其中:C為系統的比熱容;h為表面傳熱系數;T0為外部環境溫度;T為火焰溫度;β為單位體積石蠟的燃燒產熱;a為燃料供給率;n為蠟燭振子火焰中的氧濃度;E為活化能;R為摩爾氣體常數;σ為玻爾茲曼常數;n0為外部環境中的氧濃度;n為蠟燭火焰中的氧濃度;k為通過對流供氧的速率;ω1為溫度變化的特征頻率;ω2為氧濃度變化的特征頻率。

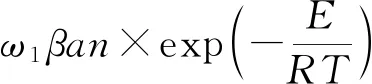
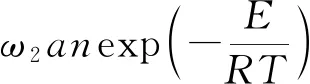
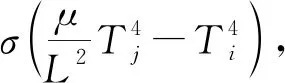
(3)

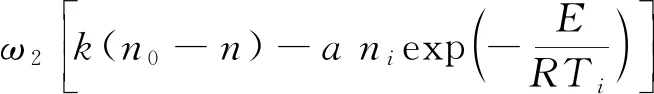
(4)

其中:μ為與氣體的光吸收速率相對應的常數;i,j=1,2且i≠j。

為便于數值計算和仿真,將上述方程去量綱化:

最終得到:

(5)

(6)

其中:i,j=1,2且i≠j;ui為第i組蠟燭組的火焰溫度的無量綱化表示;vi為第i組蠟燭組周圍氧氣濃度的無量綱化表示;ε為與特征時間常量有關的一個常數;au、av為與燃料供給速率有關的量;σ0為與玻爾茲曼常數有關的常量;c為與能量有關的常數;μ0為耦合強度,μ0=μ/L2。

分析可知,耦合振蕩主要與燃料供給率a和耦合強度μ0相關。常溫常壓下,蠟燭根數越多,蠟燭直徑越大,則燃料供給率a越大,相應的au、av越大,振蕩也就越強烈;耦合強度μ0則隨著蠟燭組間距L變大而逐漸變小。

利用MATLAB軟件對方程(5)、(6)進行時序仿真,結果如圖1所示。圖1中,縱、橫坐標的量均無量綱,下同。圖1a、圖1b所示分別為“3+3”蠟燭組的同向振蕩和反向振蕩的仿真時序圖。

圖1中,當蠟燭組中蠟燭根數為3時,應當選取au=37、av=3.7。

圖1仿真結果表明:蠟燭組間距較小時產生同相振蕩,蠟燭組間距較大時產生反相振蕩;此外,耦合振蕩還與外部環境、蠟燭種類等因素有關。

2 實驗探究

2.1 實驗裝置與條件

為了進一步探究耦合振蕩的影響因素,本文設計了一系列實驗。實驗中所用到的物品包括多種蠟燭、燃燒實驗箱、滑軌、高速攝像機(千眼狼2F04C,中國富煌君達公司)、長焦球面反射鏡、計算機等。實驗裝置及數據處理系統示意圖如圖2所示。

圖2 實驗裝置及數據處理系統示意圖

為使單組蠟燭振子的火焰可以聚攏為一束并形成振蕩,實驗中采用多支蠟燭捆綁方式,以蠟燭之間空隙最小的軸對稱或中心對稱形狀進行排布,以保證蠟燭火焰最為緊密,最大限度地減小燭芯間距。同時,為了避免周圍空氣擾動的影響,在蠟燭組外圍設置屏蔽裝置。由于屏蔽裝置較大而實驗時間很短,屏蔽裝置對實驗的影響可以忽略不計。

實驗在常溫常壓下、無風的燃燒實驗箱中進行,2個蠟燭組可以通過水平滑軌上的移動改變相互之間的距離。

2.2 實驗過程

實驗內容主要分為以下4個部分:

1) 采用不同種類蠟燭,對不同燭心間距的蠟燭火焰高速攝像,確定蠟燭種類、耦合情況和變化范圍。結果表明,選取較小直徑的蠟燭(6 mm),在中心間距20～90 mm范圍內進行實驗,可以較好地滿足實驗要求。

2) 在蠟燭組之間設置薄膜,并初步判斷傳熱形式。在2個蠟燭組之間引入一塑料薄膜,阻斷了熱對流影響后,仍能觀察到耦合振蕩現象;而引入錫紙膜,阻斷了熱對流和熱輻射的影響后,則完全觀察不到耦合振蕩的現象。這初步表明耦合振蕩是熱輻射與熱對流共同作用的結果。

3) 研究2組3根全同蠟燭振子(下文稱為“3+3”)的耦合振蕩。通過調節2個蠟燭組中心間距,從20 mm增加至90 mm,以2 mm為步幅進行多組重復實驗。

4) 繼續做“4+4”“5+5”“6+6”蠟燭組的多組實驗,觀察不同直徑蠟燭組的耦合振蕩現象。

下文以“3+3”為例,并附以“4+4”的相關數據進行對比。

3 實驗結果與分析

3.1 實驗結果

高速攝像機以500幀/s的幀率進行實驗拍攝,并利用Origin軟件進行圖像處理,得到的數據及圖像分別見表1所列和圖3、圖4所示。其中:表1所列為“3+3”“4+4”蠟燭組耦合情況與距離的關系;圖3所示為“3+3”蠟燭組振蕩頻率與蠟燭組間距的關系;圖4a、圖4b分別為“3+3”蠟燭組同向振蕩與反向振蕩對應的亮度時序圖,圖4c、圖4d分別為“4+4”蠟燭組同向振蕩與反向振蕩對應的亮度時序圖。

表1 “3+3”“4+4”蠟燭組耦合情況與距離的關系

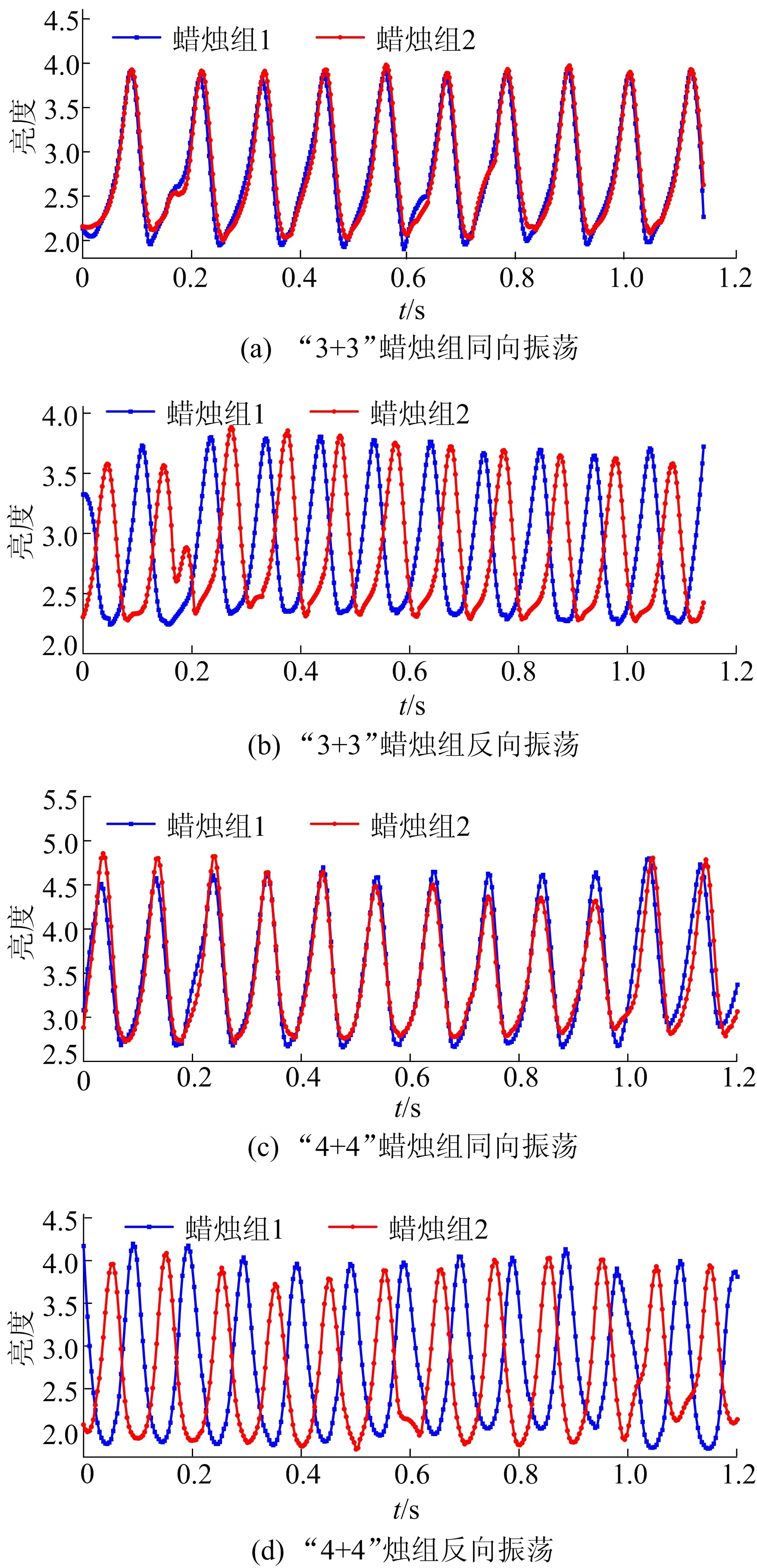
圖3 “3+3”蠟燭組振蕩頻率與蠟燭組間距的關系

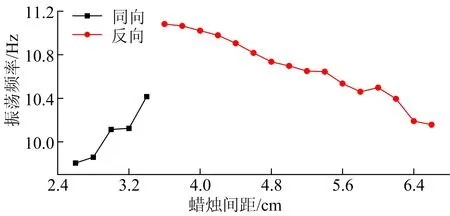
圖4 “3+3”“4+4”蠟燭組同向和反向振蕩對應的亮度時序圖

對上述數據進行分析,可得到以下結論。

1) 兩組蠟燭距離較近時,會出現同相振蕩的行為;兩組蠟燭距離較遠時,會出現反相振蕩的行為;兩組蠟燭距離超出一定范圍時,兩組蠟燭振蕩不相關。這是由于耦合強度μ0=μ/L2,當L增大時,μ0減小所致。在仿真中改變μ0的值,可以得到相應的同相或反相振蕩,如圖1a中μ0=0.50和圖1b中μ0=0.01時的情況。

2) 在同相-反相-不相關的變換交界處,會出現2種模式之一或波動的現象。這證明耦合的變化是連續的,可以用連續函數表示。

3) 在其他實驗條件一定的情況下,蠟燭直徑越大,蠟燭根數越多,相應的燃料供給率a就越大,振蕩的耦合范圍就越大,振蕩頻率也越快,表1和圖4均可得到此結論。

4) 對于不同種類的蠟燭,雖然耦合情況隨間距變化的規律一樣,但其并不完全相同。這主要是由于所選蠟燭種類不同導致燃料供應率a不同所致。

5) 以“3+3”為例,兩組蠟燭的振蕩頻率與蠟燭組間距的關系為:當2個蠟燭組間距L≤30 mm時,產生同向振蕩,振蕩頻率隨距離的增大呈遞增趨勢;當35 mm≤L≤60 mm時,產生反向振蕩,振蕩頻率隨距離的增大呈遞增趨勢,如圖3所示。

以上結論與方程(5)、(6)計算的結果相對應,說明仿真結果與實際變化趨勢一致。

3.2 熱對流在蠟燭火焰耦合振蕩中的作用

為討論熱輻射和熱對流對蠟燭火焰耦合振蕩的作用,嘗試在仿真中忽略輻射耦合項或對流散熱項,再觀察仿真中蠟燭耦合振蕩的情況。方程(5)、(6)忽略輻射耦合項、對流散熱項對應的時序仿真圖如圖5所示。

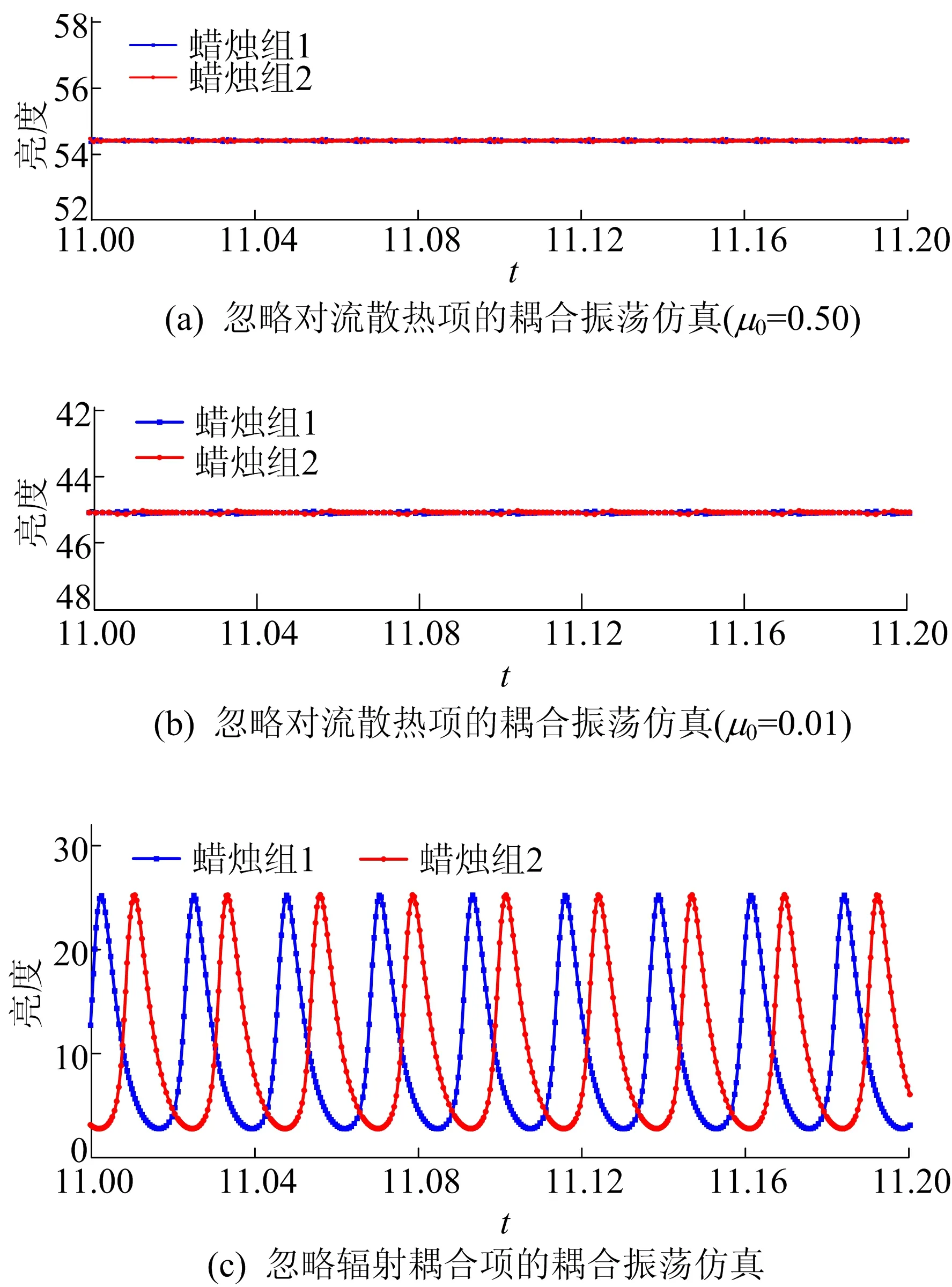
圖5 方程(5)、(6)忽略輻射耦合項、對流散熱項的時序仿真圖

從圖5a、圖5b可以看出,在仿真中忽略對流散熱項,則耦合振蕩無法產生,仿真曲線近似一條直線。

從圖5c可以看出,在仿真中忽略熱輻射耦合項,蠟燭組仍然存在耦合振蕩。

熱輻射在耦合振蕩過程中的作用體現在輻射耦合項上。當蠟燭組間距變化時,通過改變μ0值,熱輻射能夠在一定耦合范圍內調節兩組蠟燭的振蕩相位差和振蕩頻率,但熱輻射本身不足以使蠟燭組產生耦合振蕩。

對于熱對流和熱輻射的共同作用,文獻[3]研究認為熱輻射是影響傳熱的主要因素。仿真結果表明:熱輻射在耦合中確實起到一定的作用,但并非占據主導作用,熱對流才是影響蠟燭耦合振蕩的主要因素。

為了更直觀地探究熱對流的影響,本文研究了耦合振蕩蠟燭組周圍流場的特征。目前準確觀測流場數值特征較為困難,因此采用紋影法[10]對蠟燭周圍流場進行拍攝以定性分析。

紋影法拍攝的同相、反相振蕩模式下的蠟燭流場如圖6所示,反相振蕩流場中的鈍體如圖7所示。

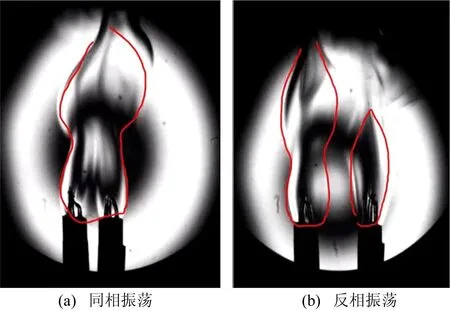
圖6 紋影法拍攝的蠟燭組振蕩火焰流場

圖7 反相振蕩流場中的鈍體

通過觀察流場,可以發現:

1) 從圖6a可以看出,同相振蕩的兩蠟燭組流場相融合,中間無明顯的外界空氣影響,此時2個蠟燭組的振蕩與捆綁在一起的1個蠟燭組的振蕩相類似。

2) 從圖6b可以看出,反相振蕩的兩蠟燭組之間的流場較為獨立,中間有明顯的外界空氣。這部分空氣基本不隨著蠟燭火焰的振蕩而上下運動。反相振蕩流場類似于卡門渦街[9]。兩者的相似之處是2個反向旋轉剪切層的渦流方向,且這2種流場都涉及到剪切層的結構從對稱過渡到交錯的過程。此外有研究表明[8],從同相振蕩到反相振蕩的轉變通常在雷諾數在幾十到幾百之間發生,這也與卡門渦街的理論范圍較為相似。因此可以認為中間的外界空氣充當了鈍體的阻礙作用,如圖7紅色部分所示。

3) 在同相振蕩時,蠟燭火焰外邊緣包絡接近于同步,且內邊緣包絡幾乎為豎直的線條;反相振蕩時,蠟燭火焰外邊緣包絡存在一定的相位差,且內邊緣包絡多為彎曲的線條。

3.3 耦合振蕩的機理解釋

從渦動力學的角度,對蠟燭火焰耦合振蕩機制進行探究。單組蠟燭火焰振蕩的機制可以解釋為:周圍的低密度熱氣體在浮力的作用下向上加速,在火焰外部形成薄剪切層;剪切層從火焰底部開始向上卷成一個環形渦;環形渦不斷增強,逐漸使火焰變形,形成細頸形;細頸折斷,導致火焰夾斷;分離的火苗在環形渦的帶動下上升,其余部分進入下一周期循環,如圖8所示。

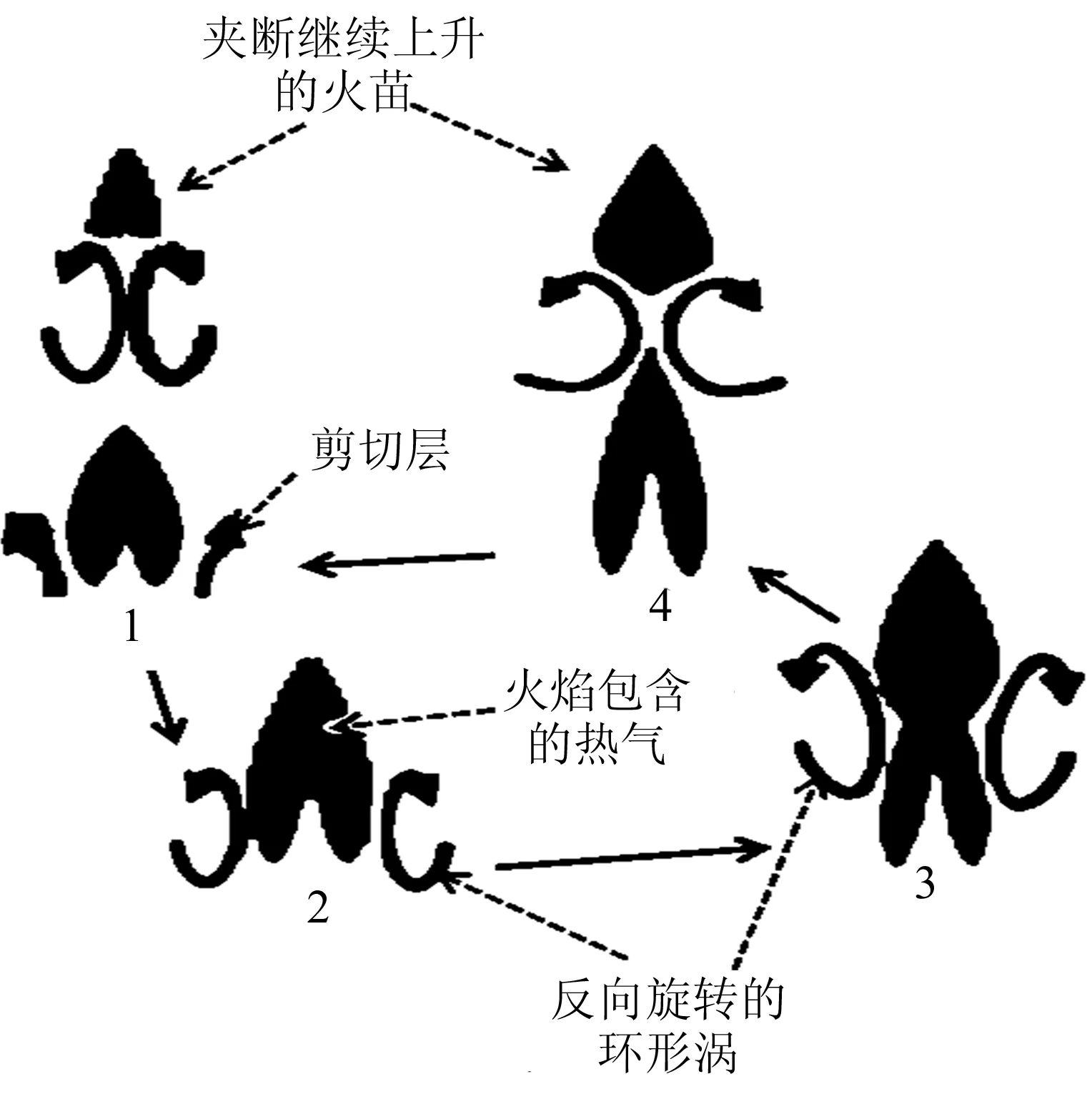
圖8 單組蠟燭振子火焰周期性振蕩

同相振蕩蠟燭火焰的剪切情況如圖9所示。從圖9可以看出,2組同相振蕩蠟燭火焰的剪切情況與單組蠟燭振子的剪切情況極為相似,環形渦旋的卷起均出現在2個火焰的振蕩模式中。

圖9 同相振蕩蠟燭火焰的剪切情況

以上研究表明,對于單組蠟燭火焰振蕩的機理可以推廣到2組蠟燭火焰的振蕩中。

在上述討論的基礎上,可以進一步解釋同相與反相振蕩的機制。“3+3”蠟燭組1個周期內同向與反向振蕩的連續圖如圖10所示。

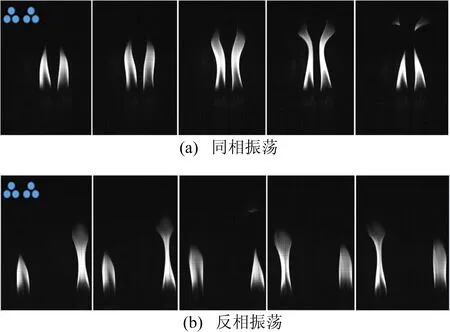
圖10 “3+3”蠟燭組1個周期內耦合振蕩連續圖

在2個蠟燭組構成的系統中,火焰同相振蕩時,2個火焰的內外邊緣都發生變形,但內邊緣變形小于外邊緣;當火焰收縮到最小高度時,它們又回到最初的位置。在每個振蕩周期中,2個火焰的發光部分從初始態開始同時向上伸長,直到達到最高火焰高度,火焰尖端的一部分被切斷,最終變成煙霧,之后2個火焰同時收縮并恢復到初始狀態,如圖10a所示。

2個蠟燭組外剪切層的渦旋同步對稱脫落,在外層剪切層上形成的旋渦的大小隨著向上移動而逐漸增大。當這些旋渦向上移動時,它們同時拉長火焰表面直至達到最大火焰高度,此時這些旋渦相互接觸,從而擠壓2個火焰尖端的邊緣,形成一團氣流。這種旋渦的不斷形成和運動導致火焰表面的反復伸長和收縮,從而產生同相振蕩。

當火焰反相振蕩時,一個火焰達到最高火焰高度時,另一個火焰處于最低火焰高度的位置,如圖10b所示。

火焰的內邊緣出現周期性變形,而外邊緣則出現較小的波動。在外部和內部剪切層上都發生了旋渦脫落,一個振蕩火焰周圍形成的渦位于另一個振蕩火焰周圍形成的渦的上方。這種旋渦脫落的方式沿著火焰的內部剪切層,從而導致火焰的交替伸長和收縮。內部剪切層上的旋渦移動速度略快于外部剪切層,旋渦的內部由于周圍熱空氣的自然對流而獲得更多的流動速度,而外部由于周圍冷空氣而獲得更低的流動速度,導致內部和外部的渦量有所不同,內部的渦量大于外部的渦量,從而產生反相振蕩。

4 結 論

本文著重對兩組全同的蠟燭振子耦合振蕩進行了實驗和理論研究。

1) 借助高速攝影技術,對蠟燭振子耦合振蕩進行了研究。隨著蠟燭組間距的改變,輻射耦合項不斷變化,熱輻射能夠在一定耦合范圍內調節2組蠟燭的振蕩相位差和振蕩頻率,從而影響耦合振蕩。

2) 通過紋影法拍攝流場,對熱對流耦合進行了研究。在蠟燭的耦合振蕩中,熱對流起到主導作用。借助同相、反相振蕩模式下蠟燭火焰流場特性的差異,可以定性判斷耦合的狀態。

3) 基于渦動力學理論解釋了耦合振蕩的機理。振蕩模式的仿真結果和流場的分析結果與實驗現象一致,與實驗結果吻合較好。