鋼筋混凝土矮塔斜拉橋地震易損性分析

王國慶, 何沛祥, 鄭 攀, 何程瑞偉

(合肥工業大學 土木與水利工程學院,安徽 合肥 230009)

易損性曲線描述了構件在給定地震動強度條件下,結構地震需求超越結構特定損傷狀態的條件概率。大量研究結果表明,結構不確定性參數會對橋梁地震響應和損傷概率造成影響[1-3],但是過多考慮結構參數不確定性將會耗費大量的時間用于有限元模型的非線性時程分析。因此,一些研究者利用代理模型結合實驗設計方法或抽樣方法建立易損性曲線,文獻 [4-7] 研究表明,該種方法能夠在保證計算結果精度的情況下,大幅縮短計算所需的時間。本文采用神經網絡與均勻設計法相結合的方式建立構件的易損性曲線。在獲取構件易損性曲線后,如何獲取橋梁系統的易損性曲線成為相關研究的焦點[8-9]。根據串聯模型系統的失效概率公式,系統易損性曲線求解關鍵在于聯合失效概率的求解。采用Copula函數建立多維聯合分布時,不需限制邊緣分布函數的類型,能夠靈活方便地構造多維聯合分布,因此,該函數具有更廣泛的適用性和可擴展性,已經被廣泛應用于金融[10]、水利[11]、防災減災等領域。文獻[12-13]將Copula函數與系統易損性相結合,但主要應用于受力較簡單的梁式橋,對于受力更復雜的矮塔斜拉橋的相關研究較少。因此,本文引入Copula函數,研究矮塔斜拉橋的系統易損性曲線,并與一階界限法[8]比較,驗證該方法的可行性與適用性。

1 神經網絡方法與Copula函數介紹

1.1 基于神經網絡的橋梁地震易損性計算方法

人工神經網絡是一種模擬人類神經細胞工作的抽象數學模型,用于模擬一些無法用數學公式嚴格推導的數學問題。基于人工神經網絡與均勻設計法相結合的易損性計算方法如下所述。

1) 選取試驗方法、結構不確定性參數和地面運動記錄,并將其組成橋梁地震動樣本。

2) 采用非線性時程分析法獲取構件的地震響應。

3) 將步驟1)和步驟2)中的數據進行配對,組成神經網絡訓練樣本。

4) 調整神經網絡參數和結構,直到預測結果精度達到要求。

5) 利用訓練好的神經網絡對隨機抽樣的橋梁地震動樣本進行預測,并建立易損性曲線。

1.2 基于Copula函數的系統易損性分析理論

Copula函數、聯合分布函數和邊緣分布函數之間存在著必然邏輯關系,任何聯合分布函數均可由Copula函數和邊緣分布函數復合而成[14],即

F(x1,x2,…,xn)=

C(F1(x1),F2(x2),…,Fn(xn))

(1)

其中:F(x1,x2,…,xn)為聯合分布函數;C(·)為Copula函數;Fi(xi)為邊緣分布函數。

橋梁結構系統可以看成由多個構件組合而成的串聯系統。串聯系統的失效概率Psys計算公式為:

…+(-1)n-1Pijk…

(2)

其中:Pi為系統中第i個構件單獨失效的概率;Pij為系統中第i個構件和第j個構件同時失效的概率;n為系統中所有可能失效構件的數目。

對于橋梁系統易損性曲線,可采用Copula函數求解各個構件之間的聯合分布函數(概率)。式(2)中引入Copula函數后,系統的失效概率為:

(-1)n-1C(Pi,Pj,Pk,…)

(3)

求得構件失效概率和構件之間的Copula函數后,采用式(3)便可算出系統失效概率,從而得到系統易損性曲線。

2 計算實例

2.1 矮塔斜拉橋概況及有限元模型

某在建鋼筋混凝土矮塔斜拉橋跨徑為(80+150+80) m,主梁采用三向預應力混凝土截面梁,跨中梁高為5.6 m,支點梁高為4.0 m。主墩為雙肢薄壁墩,單肢矩形截面尺寸為15.0 m×1.8 m。過渡墩為雙柱矩形墩,截面尺寸為2.0 m×3.0 m。主塔采用塔高為26.5 m的獨柱矩形塔,截面尺寸為3.0 m×5.0 m。全橋呈扇形雙索面布置96根斜拉索。1/2實例橋梁示意圖如圖1所示。

圖1 1/2實例橋梁示意圖

基于OpenSees軟件平臺對該橋梁進行有限元建模與分析。已有研究表明,主梁在地震作用下不易發生損壞,基本維持在彈性工作范圍之內,因此本文采用無非線性行為的彈性梁單元對主梁進行建模。斜拉索采用Truss單元模擬,過渡墩和主墩的力學行為采用基于纖維截面的非線性梁柱(Nonlinear Beam Column)單元模擬。纖維截面主要劃分為3部分,其中保護層混凝土和核心混凝土采用Concrete04本構模型,普通鋼筋采用Steel02本構模型。

橋梁結構形式為塔墩梁固結體系,邊墩支座通過給零長度單元賦予理想雙折線彈塑性材料的方式模擬,斜拉索索力的施加通過賦予對應單元初始應變的方式來模擬。構件有限元模擬示意圖如圖2所示。

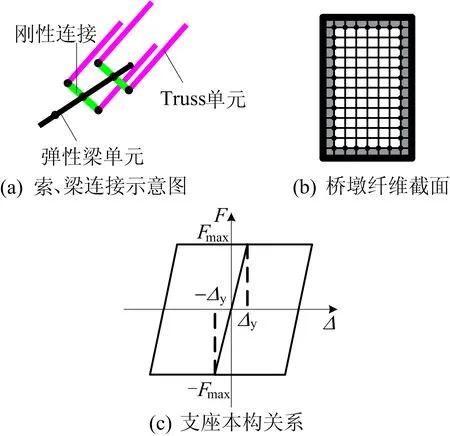
圖2 構件有限元模擬示意圖

2.2 設計變量和均勻設計方法

根據歷史震害調查資料,橋墩和支座是易于發生損壞的構件[15],應給予重點關注。因此,本文選取支座、過渡墩和主墩作為研究對象。為考慮結構參數不確定性影響,選取過渡墩核心混凝土峰值應力(fc1,core)、過渡墩核心混凝土峰值應變(εc1,core)、主墩核心混凝土峰值應力(fc2,core)、主墩核心混凝土峰值應變(εc2,core)和普通鋼筋彈性模量(Es)5個材料不確定性參數作為隨機變量。將5個隨機變量劃分為15水平,選取U15(155)均勻表進行實驗設計,共獲得15組橋梁樣本。隨機變量的對數正態分布參數見表1所列。

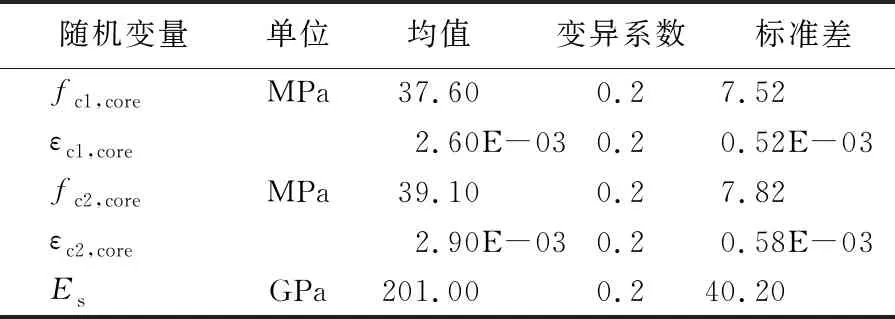
表1 5個隨機變量對數正態分布參數

2.3 地震動選取及損傷指標劃分

同一結構在不同地震波作用下的非線性時程分析結果存在較大差異[16],因此要保證時程分析結果的可靠性,應選取符合橋址場地條件和橋梁設計參數的地震波。現階段地震波主要來源于人工生成地震波和歷史地震波數據庫,本文根據文獻[17]給出的設計反應譜,從太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center,PEER)數據中匹配天然地震波。綜合考慮地震動持時、震中距等因素,最終選取15條天然地震波用于后續計算。地震波反應譜及均值反應譜曲線如圖3所示。

圖3 15條天然地震波反應譜及均值反應譜曲線

結構在地震作用下會進入彈塑性受力狀態,并發生不同程度的破壞,為便于對橋梁在地震作用下的破壞程度進行區分,常根據損傷指標的取值范圍將結構劃分為輕微破壞、中等破壞、嚴重破壞和完全破壞4種損傷狀態。本文選取支座位移μ作為支座損傷指標,根據設計文件和文獻[17]可得單向、雙向活動支座最大縱向允許位移為150 mm。支座4種損傷狀態的定義見表2所列。

表2 支座損傷狀態劃分結果

過渡墩和主墩作為壓彎構件,需同時承擔軸向壓力和地震作用下的水平剪切力,根據其受力特點,本文選取使用較為廣泛的截面彎曲曲率作為其損傷指標。截面曲率需要通過彎矩-曲率分析獲取,本文采用XTRACT軟件對過渡墩和主墩墩底截面進行建模和分析。過渡墩截面的彎矩-曲率關系曲線如圖4所示。

圖4 過渡墩截面彎矩-曲率關系曲線

根據XTRACT軟件的截面彎矩-曲率分析結果,可以得到過渡墩和主墩不同損傷狀態下的截面曲率φ取值范圍。過渡墩和主墩4種損傷狀態的劃分結果見表3所列。

表3 過渡墩和主墩損傷狀態劃分結果 單位:10-3/m

2.4 非線性時程分析及神經網絡構建

將15條天然地震波分別調幅至0.1g～1.0g(增量0.1g),并與15組橋梁樣本進行隨機配對,即可獲得150組橋梁地震動樣本。對150組橋梁地震動樣本進行非線性時程分析,得到用于神經網絡訓練的初始數據。為確保訓練的神經網絡具有足夠的精度,本文基于TensorFlow平臺進行多次試算確定網絡結構,最終選取神經元數分別為50、25的雙隱含層神經網絡,并以Relu作為其激活函數。有限元計算值和神經網絡預測值的散點圖如圖5所示。從圖5可以看出,數據點接近直線y=x,表明神經網絡預測結果具有較高的精度。

圖5 3種構件響應預測值與計算值對比

3 橋梁構件與系統易損性曲線建立

3.1 橋梁構件易損性曲線

概率地震需求模型(probabilistic seismic demand model,PSDM)是在非線性動力時程分析方法的基礎上,對結構響應進行回歸分析而衍生的一種易損性曲線建立方法。假設構件地震需求D和構件抗震能力C服從對數正態分布,根據易損性的定義可得出構件地震損傷概率Pf計算公式[18]為:

(4)

其中:D|IM為在地震動強度IM下的構件地震需求;βC、βD|IM分別為抗震能力和地震需求標準差。

采用指數函數描述D與IM之間的關系為:

lnD|IM=blnIM+lna

(5)

其中,a、b為線性回歸參數。將式(5)代入式 (4)中,Pf可進一步表示為:

(6)

由式(5)、式(6)可知,要求得構件易損性曲線,需要對D|IM與IM進行對數線性回歸分析,本文選取常用的地面峰值加速度(peak ground acceleration,PGA)作為IM,對每級PGA下的不確定性參數進行抽樣,并用神經網絡預測構件的響應值,將預測響應值與IM進行對數擬合,即可得到式(6)所示的關系式。3種構件的D與IM的線性回歸方程見表4所列。

表4 3種構件的D與IM線性回歸方程

圖6 3種構件易損性曲線

從圖6可以看出:在PGA為0.1g時,支座發生輕微破壞和中等破壞的概率分別為53.2%、31.1%,發生嚴重破壞和完全破壞的概率分別為3.0%、1.0%;主墩發生輕微破壞和中等破壞的概率分別為9.3%、1.2%,發生嚴重破壞和完全破壞的概率為0;過渡墩未發生任何狀態的破壞。在4種損傷狀態下,支座的損傷超越概率均最大,表明支座是最容易發生破壞的構件。值得一提的是,雖然不同構件在不同損傷狀態下的損傷超越概率均隨著PGA的增加而增加,但其各自增長速率不同。易損性曲線增速的快慢能夠在一定程度上反映構件抗震延性的強弱。支座發生輕微、中等破壞概率的增速較快,發生嚴重、完全破壞概率的增速較慢;主墩發生輕微、中等和嚴重破壞概率的增速相差不大,發生完全破壞概率的增速較慢;過渡墩易損性曲線的增速均較慢。綜合考慮損傷發生難易程度和抗震延性強弱,支座均為抗震能力最差的構件,其次為主墩,而過渡墩的抗震性能較好,在不同強度的地震作用下發生完全破壞的概率均較低。

3.2 橋梁系統易損性曲線

橋梁作為一個由若干構件有機組合而成的復雜結構系統,單一或部分構件的破壞或損傷往往不能夠代表整個橋梁系統的破壞或損傷。已有研究結果表明,若以單一構件的破壞或損傷來代替橋梁系統的破壞或損傷,則會高估橋梁系統的抗震能力。因此,若要更加全面地評估橋梁系統在不同強度地震作用下的損傷狀態,則需找到一種能夠合理反映橋梁構件與橋梁系統之間關系的數學模型。

由于一階界限法便于理解和使用,被廣泛應用于實際工程中,本文采用一階界限法驗證Copula函數建立易損性曲線的合理性。當橋梁結構系統為串聯系統,且各個構件之間的失效模式為正相關時,一階界限法估計的橋梁系統失效概率Psys可表示為:

(7)

其中:i=1,2,…,n;Pi為構件失效概率;n為研究范疇內構件總數。

由式(3)可知,當系統中有3個構件時,系統失效概率公式為:

Psys=P1+P2+P3-C(P1,P2)-C(P1,P3)-

C(P2,P3)+C(P1,P2,P3)

(8)

Copula函數種類眾多,采用Akaike信息準則(Akaike information criterion,AIC)可對Copula函數進行優度比選[13]。輕微破壞狀態下,支座與過渡墩之間的17種Copula函數優選結果如圖7所示。

圖7 輕微破壞下支座與過渡墩之間的Copula函數優選結果

圖7中,180Copula函數為其對應Copula函數旋轉所得,Copula函數與180Copula函數之間的關系見文獻[20],Copula函數的表達式見文獻[10]。

根據AIC,模型的擬合優度值越小,表明擬合效果越好。從圖7可以看出,在輕微破壞狀態下,支座與過渡墩之間的Copula函數中,Student Copula函數的擬合優度值最小,因此采用Student Copula函數。支座與過渡墩的Student Copula函數的圖像如圖8所示。圖8中,P支座、P過渡墩分別為支座、過渡墩輕微破壞的概率。采用AIC計算得到輕微破壞狀態下各構件之間的最優Copula函數,見表5所列。表5中:參數1表示構件之間的相關程度;參數2為Copula函數的自由度。

表5 輕微破壞下構件之間最優Copula函數及其參數

圖8 輕微破壞下支座與過渡墩Student Copula函數圖像

在獲得各構件之間的最優Copula函數后,將單個構件的損傷概率代入對應的Copula函數,即可得到構件之間聯合失效概率。將單個構件的損傷概率和構件之間的聯合失效概率代入式(8)可得系統的失效概率。在4種損傷狀態下,由Copula函數與一階界限法計算所得系統易損性曲線的對比如圖9所示。

圖9 4種損傷狀態下橋梁系統2種方法易損性曲線對比

從圖9可以看出,在4種損傷狀態下,由Copula函數計算得到的系統失效概率處于一階界限法計算結果的包絡范圍內,驗證了采用Copula函數建立系統易損性曲線的合理性。在輕微、中等、嚴重和完全破壞4種損傷狀態下,由Copula函數計算所得的失效概率與一階界限法下界的最大差值分別為0.7%、0.6%、2.5%、1.4%,與一階界限法上界的最大差值分別為7.8%、6.8%、14.3%、2.6%。從一階界限法的計算公式可知,上、下界分別表示構件之間完全不相關和完全相關情況下的系統失效概率。采用Copula函數計算得到的系統失效概率與下界的差值較小,表明構件之間的相關性較強,若采用下界表示系統失效概率,則會在一定程度上高估橋梁的抗震能力。

4 結 論

本文針對常見混凝土矮塔斜拉橋進行地震易損性分析,采用均勻設計法與神經網絡相結合的方式建立構件易損性曲線,并引入Copula函數計算基于串聯模型的橋梁系統易損性曲線,得到如下結論:

1) 對于構件易損性,在本文研究的支座、過渡墩和主墩3種構件中,支座在地震作用下最容易發生破壞,應給予重點關注;其次易出現破壞的構件為主墩,相較于輕微、中等、嚴重破壞,主墩發生完全破壞的概率較低;過渡墩出現破壞的概率最低,為安全儲備最大的構件,具有良好的抗震能力。

2) 對于系統易損性,采用Copula函數計算所得的系統易損性曲線介于一階界限法的上、下界之間,驗證了該方法計算易損性曲線的正確性。采用Copula函數計算所得系統失效概率與一階界限法上、下界差值最大分別為14.3%、2.5%,顯然更接近一階界限法的下界,表明橋梁系統各構件之間具有較強的相關關系。

3) 作為一種求解聯合分布函數的重要方法,Copula函數適用于受力較復雜的矮塔斜拉橋結構。采用該方法能夠獲得較精準的系統失效概率值,而非一階界限法所得的失效區間,可為工程抗震評估和結構設計人員提供有價值的參考。