組合式飛行器多體動力學建模與飛行力學特性

杜萬閃, 周洲*, 拜昱, 張志林, 王科雷

(1.西北工業大學 航空學院, 陜西 西安 710072; 2.中國兵器工業第203研究所, 陜西 西安 710061)

0 引言

為了使無人飛行器實現高續航性能和高機動性能的設計目標,組合式多體飛行器作為一種新概念飛行器被提出,相關的研究和試驗[1-15]在近現代航空發展史上逐步展開。組合式多體飛行器由多個單體無人機(以下稱飛行單元)通過翼尖鉸接組合而成。該構型飛行器具有較大展弦比,擁有很高的氣動效率和結構安全性;其翼尖連接采用鉸接約束,可以阻止彎矩的傳遞,有利于輕量化設計;保留了飛行單元的機動性和靈活性,兼具組合整體與分散集群的雙重優勢[1-2]。組合式多體飛行器因這些優勢在眾多領域中具有重大應用價值,特別是作為一種續航高效的臨近空間飛行器。國外極光飛行科學公司于2008年設計的Z型太陽能無人機[3]由3個單體無人機通過翼尖連接而成,晝夜飛行時通過Z型變體方式來減小電能消耗與提高太陽能能量轉換效率;Suenaga等[7]設計的翼尖鏈翼飛行器由多個小型無人機通過翼尖可釋放的鉸鏈連接而成,該飛行器以O型折疊在箱子里,通過降落傘在高空中投放,投放后其自行展開,并分離成多個小型無人機單獨執行飛行任務。國內Meng等[8]氣動彈性研究室針對多機組合式飛行器進行研究,分別于2018年12月和2019年4月成功進行雙機和三機首飛測試。此后,針對組合式多體飛行器的研究相對較少,尤其是在動力學特性分析方面。

組合式飛行器呈現出多剛體、多自由度的特點,在變形運動時會較大程度地改變氣動外形,因此不能像常規飛行器那樣將其視為單個剛體進行飛行動力學建模,而是需要建立一種包含變形自由度的飛行動力學模型。Montalvo等[12-13]基于Newton-Euler方法和非線性升力線模型對Meta Aircraft多種變體形態下的動力學特性進行了研究分析。Kothe等[14-15]基于Kane方法建立了變構型的多體飛行器動力學模型,并進行了閉環飛行試驗。文獻[16-19]基于擬坐標形式的Lagrange原理建立了包含變形自由度的動力翼傘、仿生變形飛行器等多體系統動力學模型,均取得較好的仿真效果。文獻[8-11]針對 7自由度雙機組合式飛行器展開飛行力學特性研究,其結論表明組合式飛行器存在對稱變形的相對運動特征。然而隨著鉸接單體數量的增加,組合式飛行器在飛行力學行為上會表現出不對稱的相對運動特征,甚至出現多重運動特征耦合的復雜運動形式。組合式三體飛行器相比于雙體飛行器可表現出不對稱的運動特征,更具典型性和可延拓性。本文針對組合式三體飛行器進行多體動力學建模和飛行力學特性分析,研究其在相對運動過程中的對稱運動和不對稱運動特征,以此更加全面地反映組合式飛行器的飛行力學特性信息。

本文采用擬坐標形式的Lagrange原理,針對組合式三體飛行器推導建立了8自由度動力學方程,利用計算流體力學(CFD)方法建立考慮氣動耦合效應的組合式飛行器氣動力數據庫,通過算例將所建模型與ADAMS軟件的仿真結果進行對比驗證。在此基礎上進行配平及飛行力學特性研究,分析比較組合式飛行器在不同配平狀態的動力學特性,最后基于串級PID控制方法進行增穩控制研究,可為多體飛行器的設計分析提供指導和參考。

1 組合式飛行器模型描述

如圖1所示,組合式三體飛行器由三個飛行單元組合而成,相鄰飛行單元間的翼尖連接采用鉸接約束,保留2個相對滾轉自由度。本文建模時不考慮機翼柔性影響,假設每個飛行單元均為剛體,圖1中整個組合式飛行器可劃分為3個剛體分別進行分析,中間的剛體記為飛行單元a,左側的剛體記為飛行單元b,右側的剛體記為飛行單元c。上述多剛體模型中飛行單元a具有6個自由度,飛行單元b和c相對于a各有1個自由度,即相對滾轉自由度,整個剛體模型共有8個自由度。該模型可以完整地描述飛行單元b、c與a的相對運動,反映飛行器實際的飛行工況。

圖1 組合式三體飛行器示意圖

1.1 坐標軸系定義

為了便于對多體飛行器進行運動描述和受力分析,引入如下坐標軸系:選取地面參考點Oe作為原點,依據右手定則建立鉛垂地面固定坐標軸系Oexeyeze,其中Oeze軸鉛垂向下;選取飛行單元a、b、c的質心作為原點分別建立機體坐標軸系Oaxayaza、Obxbybzb、Ocxcyczc,機體坐標軸系隨多體飛行器機體一起運動,具體如圖2所示。

圖2 組合式三體飛行器坐標軸系示意圖

1.2 擬坐標和擬速度描述

針對圖1所示的組合式三體飛行器8自由度模型,選取下列擬坐標q和擬速度w[16-17]描述該多體飛行器的位形:

(1)

式中:Ra用于描述a質心相對于地面固定坐標軸系原點Oe的位移;Ja用于描述a體坐標軸系相對于地面固定坐標軸系的歐拉姿態角;Jba和Jca分別用于描述b和c體坐標軸系相對于a體坐標軸系的相對滾轉角,以矢量形式給出;va為飛行單元a質心相對于地面固定坐標系的速度(在a體坐標軸系下表示);ωa為飛行單元a相對于地面固定坐標軸系的轉動角速度(在a體坐標軸系下表示);ωba和ωca分別為b和c體坐標軸系相對于a體坐標軸系的相對滾轉角速度(分別在b和c體坐標軸系下表示),以矢量形式給出。上述擬坐標和擬速度的分量形式表示如下:

(2)

(3)

1.3 算例模型參數

本文采用的組合三體飛行器算例模型如圖3所示,表1給出了算例模型所用飛行單元的基本參數,單體模型為上單翼布局,機翼展長3.2 m,弦長0.3 m,展弦比約10.6,具體如圖4所示,圖4中Oxyz為單體模型的機體坐標軸系。

表1 飛行單元基本參數

圖3 組合式三體飛行器模型

圖4 單體飛行器模型

2 多體飛行器系統受力分析

組合式三體飛行器在巡航狀態平飛時,多體系統所受外力主要包括氣動力、重力和螺旋槳拉力等。 其中,各個飛行單元之間存在氣動耦合效應,采用CFD計算方法建立考慮氣動耦合效應的組合式飛行器氣動力數據庫,并對飛行器系統進行受力分析。

2.1 CFD方法建立氣動力數據庫

組合式飛行器系統的飛行運動是區別于常規飛行器飛行的特殊運動形式,相關的CFD 數值仿真和風洞模擬仿真實驗[20]證明組合式飛行器系統采用多個單機以翼尖鉸接的形式實現復合飛行時,各個單機的流場會產生氣動耦合效應,其氣動特性相比單機飛行時存在顯著變化。為了表征這種氣動耦合效應對單機氣動特性的影響,采用CFD方法建立組合式三體飛行器氣動力數據庫。

由參考文獻[21-22]關于多體飛行器系統氣動耦合效應的研究可知,非定常效應對多體飛行器飛行的動態特性影響較小。因此在準定常假設下簡化計算組合式飛行器系統內部相對滾轉過程中飛行單元的氣動力,其具體形式以多項式給出,即

(4)

(5)

具體地,建立氣動力數據庫的CFD仿真內容、氣動參數和計算方法如表2所示。

表2 氣動力數據庫建立方法

在進行CFD計算時,采用結構嵌套網格進行組合式飛行器的流場劃分,各飛行單元采用O-H型網格拓撲,背景網格遠場取50倍機體長度,機體表面第1層網格高度y+≈0.6,網格總節點數978萬。網格情況如圖5和圖6所示。機體表面為無滑移邊界條件,基于定常RANS方程進行流場求解,湍流模型采用SST模型,求解采用Roe隱格式,空間離散均為2階精度。

圖5 單體飛行器網格分布

圖6 組合式三體飛行器網格分布

在建立氣動力數據庫時,選取迎角α、側滑角β以及相對滾轉角φba、φca為基準變量,然后通過CFD方法便可計算得到不同工況下組合式三體飛行器系統內各個飛行單元的氣動特性。當相對滾轉角φba=φca=0°時,各個飛行單元氣動參數隨迎角α和側滑角β的變化曲線如圖7所示,另外在分析飛行單元氣動參數隨側滑角β變化時迎角取α=0°。

圖7 飛行單元氣動參數隨迎角α和側滑角β變化

在迎角α=0°和側滑角β=0°的工況下分析相對滾轉角φba、φca對各個飛行單元氣動特性的影響。在分析相對滾轉角φba的影響時,令φca=0°,可以得到各個飛行單元的氣動參數隨著相對滾轉角φba的變化情況。同理,令φba=0°即可得到各個飛行單元的氣動參數隨相對滾轉角φca的變化情況。不難看出,在此情況下相對滾轉角φba、φca對各個飛行單元氣動特性的影響具有對稱性。因此此處只給出在φca=0°時各個飛行單元的氣動參數隨著相對滾轉角φba的變化曲線,如圖8所示。

圖8 飛行單元氣動參數隨相對滾轉角φba變化

螺旋槳拉力模型通過參考文獻[23]給出,即

(6)

式中:Ct為螺旋槳拉力系數;ρ為大氣密度;ns為轉速(r/min);Dp為槳盤直徑。對于算例模型所用的螺旋槳,通過螺旋槳拉力試驗可測得不同油門桿量δt下的螺旋槳轉速ns,擬合得到電機轉速與油門桿量的二次函數關系式為

ns=(-4.44δt+15.65δt-0.02)×103

(7)

式中:δt值為0～1。螺旋槳的前進比[23]定義為

(8)

(9)

2.2 8自由度系統受力分析

組合式三體飛行器系統所受合外力在飛行單元a體坐標軸系下表示為

(10)

式中:Ga、Gb、Gc為各飛行單元所受重力;Fa,a、Fa,b、Fa,c為各飛行單元所受氣動力在其體坐標軸系下的投影;Ft,a、Ft,b、Ft,c為各飛行單元所受螺旋槳拉力。

系統所受合力矩在飛行單元a體坐標軸系下表示為

(11)

式中:Ma,a、Ma,b、Ma,c為各飛行單元所受氣動力矩在其體坐標軸系下的投影。

飛行單元b和c所受合力矩在其體坐標軸系下分別表示為

(12)

(13)

3 擬坐標形式的組合式飛行器多體動力學模型

3.1 8自由度組合式飛行器動力學建模

擬坐標形式的Lagrange動力學方程[17-19]為

(14)

運動學方程為

(15)

式中:L為拉格朗日函數;H和B為系數矩陣;Q*為廣義力矩陣。

針對圖4所示的8自由度組合式飛行器算例模型,將重力作為外力處理,忽略其他彈性勢能,系統的拉格朗日函數L取所有剛體的動能之和,其中每個飛行單元的動能由平動動能和轉動動能組成,具體形式為

(16)

(17)

(18)

(19)

式中:ma、mb、mc和Ia、Ib、Ic分別為各個飛行單元的質量和慣量張量矩陣(對質心,本體坐標軸系)。

(20)

(21)

將式(20)、式(21)代入式(14)整理得到8自由度組合式三體飛行器動力學方程組:

(22)

式中:狀態變換矩陣

(23)

Da、Dba、Dca分別為飛行單元a、b、c的歐拉角時間導數到其體軸系轉動角速度的坐標轉換矩陣;系統廣義力矩陣

(24)

系數矩陣

(25)

據式(22),給定初始運動狀態就可以求解組合式飛行器系統的飛行特性。

3.2 動力學模型驗證

建立8自由度動力學模型的目的是開展精確完整的飛行特性仿真,以便獲得更接近于組合式飛行器實際飛行工況的飛行數據。為了驗證本文動力學模型的準確性,對組合式三體飛行器進行建模,在相同工況下對比本文模型和所建仿真模型的仿真結果。

圖9 飛行單元a狀態量響應

為驗證本文模型對相對滾轉運動描述的準確性,在仿真初始狀態的基礎上,設定不同狀態的相對滾轉角φba、φca(見表3)進行求解,得到多體系統相對滾轉運動響應如圖10所示。

表3 不同初始狀態的相對滾轉角

圖10 不同初始狀態的相對滾轉角響應

由仿真結果對比分析知,兩種模型在相同工況下的仿真結果吻合度很高,本文所建模型可以有效反映2個相對滾轉運動的變化情況,能夠精確、完整地描述多體飛行器空間運動的位形,驗證了本文組合式多體飛行器建模方法的有效性和準確性。

3.3 動力學方程組線性化及其狀態空間形式表達

為便于研究組合式飛行器系統的飛行力學特性,本節在3.1節建立的8自由度全量非解耦動力學方程組的基礎上,運用小擾動法[24-25]將其進行線性化處理,推導其狀態空間形式[26]的小擾動動力學方程組。由2.1節氣動力和螺旋槳拉力模型可知,舵面偏轉和油門桿量分別影響氣動力和螺旋槳拉力大小,引入操縱變量κ=[κ1,κ2,κ3,…]T表征舵量和油門輸入,此時可將非線性方程式(22)表達成矢量形式:

(26)

(27)

式(26)、式(27)形式下的動力學方程方便進行配平方程求解及穩定性分析。在規定好未知配平量及配平自由度后,求解式(27)即可給出配平狀態解F0。

對式(26)、式(27)在配平狀態下進行小擾動線性化處理,其小擾動線性化方程為

(28)

式(28)的狀態空間形式為

(29)

式中:

(30)

(31)

(32)

4 組合式飛行器配平及飛行力學特性分析

根據飛行動力學模型,本節對組合式三體飛行器進行配平方案及飛行力學特性分析。為了簡化分析計算,配平求解選擇定直平飛狀態作為分析工況。

4.1 配平方案分析

組合式三體飛行器相比常規飛行器多出2個自由度,其飛行力學模型相比傳統飛行力學模型具有顯著不同。在翼尖鉸接的形式下,每個飛行單元的滾轉角不再保持一致,存在相對滾轉運動。這就意味著此飛行器在配平時不僅要考慮整體縱向力和力矩平衡,還要保證其內部橫側向相對滾轉力矩平衡,所以在求解配平方程時需要根據實際情況來選擇配平變量。

組合式無人機的配平操縱由各個飛行單元的執行機構組合運作完成,每個飛行單元具有1個螺旋槳、2個副翼控制面、1個升降舵控制面和1個方向舵控制面。在定直平飛工況下,規定每個飛行單元的副翼控制面聯動,偏轉大小相同,方向相反即只對滾轉運動起作用;3個飛行單元的油門桿量保持一致;3個飛行單元的方向舵和升降舵聯動,偏轉大小方向均相同。

在進行配平變量組合時,為了保持組合式飛行器整體處于定直平飛狀態,聯動升降舵和油門桿量用來平衡組合式飛行器系統整體的俯仰運動方程;分開作動的副翼既要用來平衡組合式飛行器系統整體滾轉運動方程,也要同時用來平衡系統內部的相對滾轉力矩;聯動的方向舵則用來平衡組合式飛行器系統的偏航運動方程。由此知,在定直平飛配平狀態下,組合式三體飛行器的未知配平量為

(33)

式中:δe為一致的升降舵偏角,即δe,a=δe,b=δe,c,其中δe,a、δe,b、δe,c分別為飛行單元a、b、c的升降舵偏角;δt為一致的油門桿量,即δt,a=δt,b=δt,c,其中δt,a、δt,b、δt,c分別為飛行單元a、b、c的油門桿量;δr為一致的方向舵偏角,即δr,a=δr,b=δr,c,其中δr,a、δr,b、δr,c分別為飛行單元a、b、c的方向舵偏角;δa,a、δa,b、δa,c分別為飛行單元a、b、c的副翼偏角。未知的配平參量有8個,與系統的自由度一致,配平方程可解。

將未知配平量χ代入式(27),并令方程左邊取0,即

F(q,w,κ)=0

(34)

給定初始狀態便可解算未知配平量,得到配平狀態解F0。

本節采用第1.3節給出的組合式三體飛行器算例模型,在飛行工況的空氣密度為1.225 kg/m3、飛行速度為10 m/s、飛行迎角為0°的條件下,求解得到兩個配平狀態,配平計算結果如表4所示。

表4 配平分析結果

由配平計算結果知,在給定飛行速度和迎角時,該組合式三體飛行器存在兩個配平點,這與常規飛行器在給定飛行速度或迎角后只有一個配平點具有顯著不同。在配平點1處整個飛行器呈“對稱下反”狀態,在配平點2處整個飛行器呈“對稱上反”狀態,如圖11所示。在每個配平狀態下,配平結果全機縱向對稱,升降舵偏角由于給定了聯動條件,3個飛行單元偏角一致;3個飛行單元油門桿量相同、方向舵偏角均為0°;中間飛行單元a副翼偏角為0°,右側飛行單元b和左側飛行單元c的副翼偏轉大小相同、方向相反;兩個相對滾轉角大小相同、方向相反。由此可知,與常規飛行器在配平時只需考慮縱向力和力矩平衡相比,組合式飛行器還需保證橫側向受力平衡和相對滾轉力矩平衡,并且其剛體飛行力學縱向和橫側向的動力學方程不能解耦。

圖11 兩種配平狀態

4.2 相對滾轉運動靜穩定性分析

相比常規飛行器多出2個相對滾轉運動是組合式三體飛行器的顯著特點,在兩種配平狀態下研究其靜穩定[24]特性。假設飛行器在配平狀態下受到較小相對滾轉角擾動時,各飛行單元受到的升力大小保持不變。

圖12 “對稱下反”狀態相對滾轉運動靜穩定性分析

圖13 “對稱上反”狀態相對滾轉運動穩定性分析

由以上分析知:飛行器在“對稱下反”配平狀態的相對滾轉運動具有靜穩定性;在“對稱上反”配平狀態的相對滾轉運動靜不穩定,需要增穩控制加以改善。

4.3 組合式飛行器動力學特性分析

表5 配平狀態運動模態分析

表6 新生運動模態特征向量分析

當特征根為共軛復根λ1,2時,對應模態為振蕩模態,其特征根形式和時間常數t定義分別為

(35)

(36)

式中:ζ為阻尼比;ωn為自然頻率。

當特征根為單實根λ時,對應模態為非振蕩模態,其時間常數取半衰期t1/2(模態收斂時振幅變為初始振幅一半的時間)或倍幅時t2(模態發散時振幅變為初始振幅2倍的時間),其特征根形式和時間常數定義如下:

(37)

(38)

(39)

通過對比分析表5中的結果可以發現,除了傳統飛行力學模態以外,組合式三體飛行器還多出 4個新生運動模態。為了便于分析新生運動模態的特性變化規律,表6列出了兩種配平狀態下4個新生運動模態的特征向量(忽略10-4數量級以下的參數),可以發現其中2個新生運動模態主要與縱向運動狀態量qa、θa和相對滾轉運動狀態量ωba、ωca、φba、φca有關,將其命名為復合對稱運動模態1和復合對稱運動模態2,在這 2個模態中整機具有對稱的相對滾轉運動特征;另外兩個新生運動模態與橫側向運動狀態量pa、ra、φa、ψa、ωba、ωca、φba、φca有關,將其命名為復合反對稱運動模態1和復合反對稱運動模態2,在這2個模態中整機具有不對稱的相對滾轉運動特征。結合表6特征向量分析可知,新生運動模態具備如下的運動特性:

1)復合對稱運動模態1 和復合對稱運動模態2是相對滾轉角Δφba、Δφca相對于俯仰角Δθa以及相對滾轉角速度Δωba、Δωca相對于俯仰角速度Δqa變化較大的對稱運動模態;

2)復合反對稱運動模態1和復合反對稱運動模態2是相對滾轉角Δφba、Δφca和滾轉角Δφa的變化幾乎同量級、偏航角Δψa變化較小以及相對滾轉角速度Δωba、Δωca和滾轉角速度Δpa變化幾乎同量級、偏航角速度Δra變化較小的反對稱運動模態。

在“對稱下反”配平點1處,該飛行力學系統短周期模態、長周期模態、滾轉模態以及荷蘭滾模態均呈收斂狀態,螺旋模態發散,4個新生運動模態均處于收斂狀態。飛行器的螺旋模態發散,且倍幅時較短,當飛行器系統受到橫側向擾動后,其橫側向相關狀態量會快速發散,這會影響飛行穩定性,需要通過增穩控制系統加以改善。在“對稱上反”配平點2處,該飛行力學系統短周期模態、長周期模態、滾轉模態、荷蘭滾模態、螺旋模態均收斂。對于該配平點處的新生運動模態,飛行器的復合對稱運動模態2和復合反對稱運動模態2均發散,而且倍幅時很短,當飛行器的相對滾轉運動受到擾動后,這兩個模態會快速發散,飛行器在無控狀態下無法穩定飛行,這與傳統構型飛行器有很大差別。由此可知,組合式三體飛行器系統若以“對稱上反”姿態飛行,需要采用合理的控制策略來保證其穩定性。

對比表5中兩種配平狀態的傳統飛行力學模態可知,“對稱下反”配平點1處飛行器的荷蘭滾模態阻尼比較大,模態特性較好,但螺旋模態是發散的。“對稱上反”配平點2處飛行器的螺旋模態相較于“對稱下反”配平點1變為穩定收斂,但荷蘭滾模態阻尼比下降,模態特性變差。根據參考文獻[24],機翼上反效應可以有效增強螺旋模態穩定性,組合式三體飛行器“對稱上反”狀態就相當于增強了整體機翼上反效應,改善了飛行器螺旋模態特性,而荷蘭滾模態特性則相對變差。

表7列出了文獻[8]雙機組合形式模態特征根,通過對比分析知組合式三體飛行器比雙機組合飛行器多出兩個復合運動模態,并且前者的4個新生運動模態還可以按照運動特性劃分為復合對稱運動和復合反對稱運動兩類,如圖14和圖15所示。根據文獻[8-11],雙機組合形式下的復合運動模態均具有縱向對稱運動特征。結合以上分析知,組合式三體飛行器表現出雙機組合形式不具備的復合反對稱運動模態,可以更為全面地反映此類組合式飛行器的飛行力學特性信息。復合運動模態的增多也意味著組合式三體飛行器的動力學特性更加復雜,其飛行控制系統的設計難度和復雜度也會隨之增加。

表7 雙機組合運動模態

圖14 復合對稱運動

圖15 復合反對稱運動

4.4 系統開環時域仿真分析

基于全量非解耦的狀態空間模型搭建8自由度飛行器的時域仿真模型,并分別在“對稱下反”配平點1和“對稱上反”配平點2處,給定相同的Δφba=2°、Δφca=-2°初始對稱擾動,得到相對滾轉運動狀態量的自由響應曲線,如圖16和圖17所示。

圖16 “對稱下反”配平點1處系統自由響應

圖17 “對稱上反”配平點2處系統自由響應

根據自由響應曲線,飛行器在“對稱下反”配平狀態下受到Δφba=2°、Δφca=-2°的對稱初始擾動時,兩個相對滾轉角速度和相對滾轉角均處于收斂狀態;飛行器在“對稱上反”配平狀態下受到相同初始擾動時,兩個相對滾轉角速度和相對滾轉角均快速發散,這與4.3節模態特征根分析結果一致。

在“對稱下反”配平點1處,給定Δφba=Δφca=2°的不對稱初始擾動,得到系統相關狀態量的自由響應曲線如圖18所示。根據自由響應曲線,“對稱下反”配平狀態下的相對滾轉運動受到不對稱初始擾動時表現出發散的特征,這是因為不對稱擾動誘發了組合式飛行器系統螺旋模態發散,進一步導致其相對滾轉運動發散。

圖18 配平點1處不對稱擾動下系統自由響應

根據以上分析,在給定飛行速度和迎角時,該組合式三體飛行器在兩個配平狀態下的動力學特性有顯著不同。在“對稱下反”配平點1處,4個復合運動模態均收斂,但螺旋模態發散;當飛行器受到對稱相對滾轉擾動時系統的自由響應是穩定收斂的,當受到不對稱擾動時系統的螺旋模態會快速發散而進一步導致相對滾轉運動發散。在“對稱上反”配平點2處,系統存在1個復合對稱運動模態和1個復合反對稱運動模態是發散的,飛行器相對滾轉運動受擾動后的自由響應會快速發散。

由此知,無論在配平點1還是配平點2處,飛行器都存在不穩定的模態特征根,在沒有增穩控制系統時,飛行器無法長期保持平穩飛行,特別是當飛行器處于“對稱上反”狀態時,相對滾轉運動受到擾動后便會迅速發散。為了保證組合式飛行器在任一配平狀態下都能平穩飛行,飛行器需要采取合理的增穩控制策略來使其飛行力學系統鎮定。

5 增穩控制系統設計

經過對組合式三體無人機的配平及飛行力學特性分析知,該飛行器在無控狀態下無法長期保持穩定飛行。基于串級PID控制器設計方法,設計組合式飛行器的增穩控制器,驗證增穩控制策略的有效性。

5.1 串級PID控制器

PID控制器是由比例環節、積分環節和微分環節組成的經典反饋控制器,在科學研究與工業控制中得到極其廣泛的應用。PID控制的基礎是比例控制,積分控制可消除穩態誤差,但可能增加超調;微分控制可加快系統響應速度并減弱超調趨勢。PID控制律可表達為

(40)

式中:KP為比例系數;KI為積分系數;KD為微分系數。

串級PID控制器考慮了從執行機構到狀態量響應的時間遲滯影響,控制效果相比傳統單個PID控制器大幅提升。在設計姿態增穩控制器時,舵面(升降舵等)為整個操縱機構的執行機構,舵面變化會改變飛行器受到的外力矩,從而產生姿態角速度,經過時間積分后姿態角發生變化。在上述控制過程中,從舵面輸入到姿態角響應存在時間滯后,導致使用舵面直接控制姿態角的效果不佳;但若在內環增加舵面到姿態角速度的控制回路,控制效果就可以得到大幅提升。外環PID控制器使用目標姿態角與實時姿態角得到目標姿態角速度,在此過程中為了避免積分減慢響應速度、微分引入噪聲,使用比例控制器效果較好。內環PID控制器則可以根據實際情況選擇,對響應速度要求較高則選擇PD控制器,對穩態特性、超調等要求較高則選擇PI控制器。

5.2 增穩控制方案

針對多輸入多輸出(MIMO)系統的控制律設計,可以將其簡化為多個單輸入單輸出(SISO)系統的控制律設計。本文針對組合式三體飛行器系統制定如下增穩控制方案:

1)組合式飛行器在兩個配平狀態處縱向運動穩定性均良好,因此主要針對其橫側向運動設計增穩控制系統;飛行器系統滾轉角φa和相對滾轉角φba、φca的增穩控制均采用比例-比例積分(P-PI)形式的串級PID控制器。

2)規定飛行單元a的副翼舵偏δa,a用于滾轉角φa的增穩控制,利用滾轉角φa作為外環PID控制器的反饋量,利用滾轉角速度pa作為內環PID控制器的反饋量。目標滾轉角與實時滾轉角作差通過外環比例控制器得到目標滾轉角速度,目標滾轉角速度與實時滾轉角速度作差經過內環比例積分控制器輸出舵偏δa,a,飛行單元a副翼偏轉以達到滾轉角φa的增穩目的。其控制律結構為

(41)

式中:φa,c、pa,c滾轉角指令值和滾轉角速度指令值;φa、pa為實時滾轉角和滾轉角速度;KP,φ、KP,p、KI,p為控制律參數。

3)規定飛行單元b、c的副翼舵偏δa,b、δa,c分別用于相對滾轉角φba、φca的增穩控制,分別利用相對滾轉角φba、φca作為外環PID控制器的反饋量,利用相對滾轉角速度ωba、ωca作為內環PID控制器的反饋量。目標相對滾轉角與實時相對滾轉角作差通過外環比例控制器得到目標相對滾轉角速度,目標相對滾轉角速度與實時相對滾轉角速度作差經過內環比例積分控制器輸出舵偏δa,b、δa,c,飛行單元b、c的副翼偏轉以達到相對滾轉角φba、φca的增穩目的。其控制律結構為

(42)

(43)

式中:φba,c、φca,c為相對滾轉角指令值;ωba,c、ωca,c為相對滾轉角速度指令值;φba、φca和ωba、ωca分別為實時相對滾轉角和實時相對滾轉角速度;KP,φ、KP,ω、KI,ω為控制律參數。

由增穩控制方案知,該方案可以實現直接對相對滾轉運動進行控制,相較于文獻[8-9]通過控制每個單體飛行器的滾轉角間接控制飛行器相對滾轉運動的方案具備優越性。因為本文的擬坐標Lagrange建模方法將兩個相對滾轉角作為狀態量進行解算,非常方便飛行控制系統設計。整個增穩控制系統設計思路如圖19所示,在MATLAB/Simulink軟件中搭建增穩控制系統進行時域仿真分析,仿真系統框圖如圖20所示,圖20中P表示比例控制器,PI表示比例積分控制器。

圖19 增穩控制系統設計思路圖

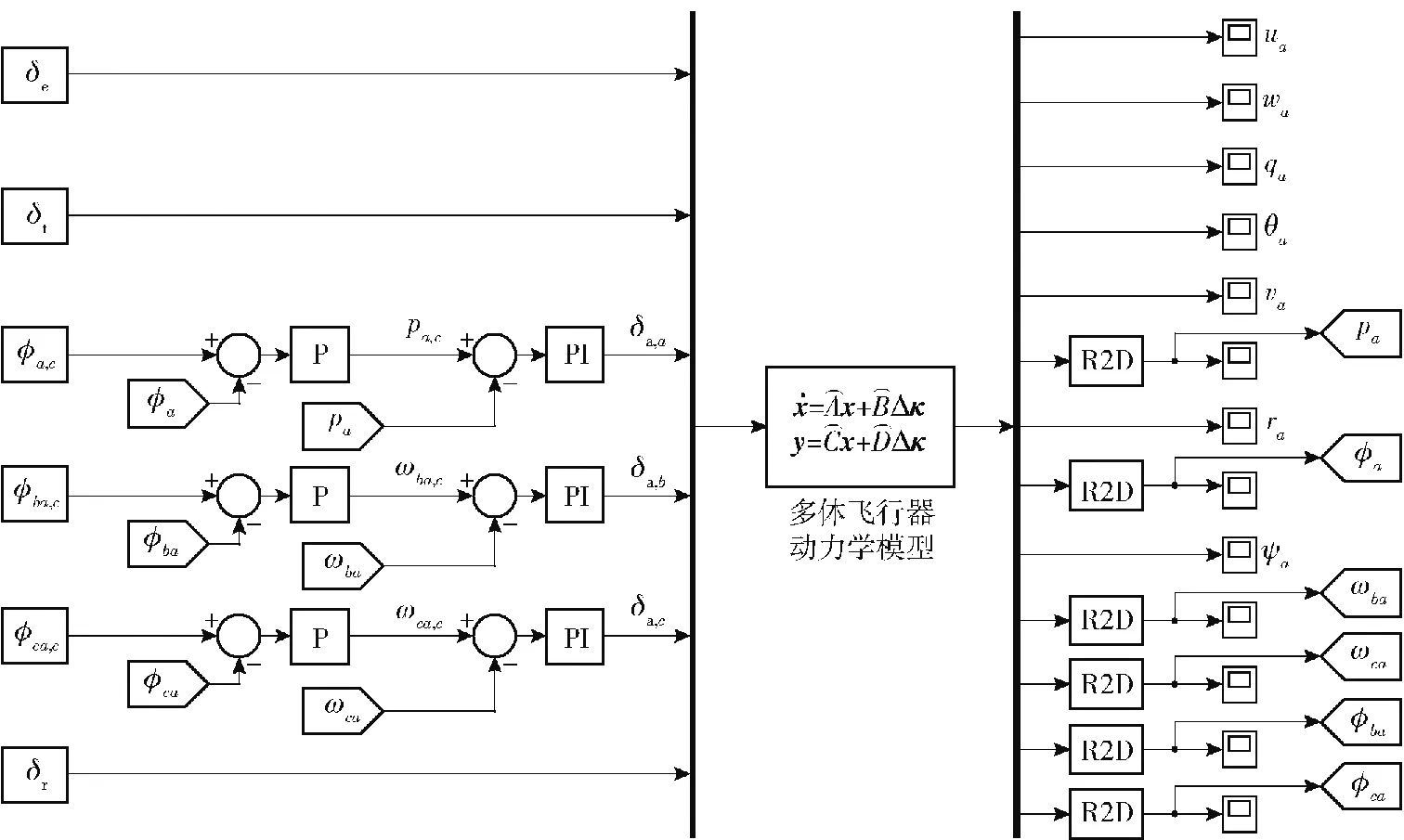
圖20 Simulink仿真框圖

為了驗證本文增穩控制方案的有效性,將橫側向姿態角指令值φa,c、φba,c、φca,c置0°,在“對稱上反”配平點2處給定組合式三體飛行器Δφba=2°、Δφca=-2°的對稱初始擾動,得到兩個相對轉角速度和相對滾轉角的時域響應曲線如圖21所示。由響應曲線可知,加入增穩控制系統后,相對滾轉角在1 s左右便收斂為0°,相對滾轉角速度在1 s處收斂至0°/s附近,穩態誤差在1%以內。對比圖17的自由響應曲線可知,該增穩控制系統有效,可以快速鎮定發散的飛行力學系統。增穩后的組合式三體飛行器能夠在配平點2處以“對稱上反”姿態平穩飛行。

圖21 增穩控制后配平點2處對稱擾動響應

在“對稱下反”配平點1處,給定飛行器系統Δφba=Δφca=2°的不對稱初始擾動,得到相關狀態量的時域響應曲線如圖22所示。由圖22可知,飛行器系統橫向運動狀態量均呈快速收斂狀態,對比圖18不對稱擾動下系統的自由響應曲線可知,增穩控制方案可以有效抑制不對稱擾動誘發的螺旋模態發散現象,同時可以鎮定發散的相對滾轉運動,從而保證飛行器在配平點1處以“對稱下反”姿態可以保持長久穩定飛行。

圖22 增穩控制后配平點1處不對稱擾動響應

6 結論

本文通過CFD方法建立了考慮氣動耦合效應的組合式三體飛行器氣動力數據庫,基于擬坐標形式的Lagrange原理推導出3體8自由度多體動力學模型,在此基礎上進行配平及飛行力學特性分析,并采用串級PID控制方法設計了組合式飛行器的增穩控制系統。得出以下主要結論:

1)組合式三體飛行器的動力學模型呈現多剛體、多自由度特點,常規飛行器的單剛體6自由度動力學建模方法不再適用。針對其飛行時的運動特點,利用擬坐標形式的Lagrange原理建立了考慮飛行單元間氣動耦合效應、反映相對滾轉運動的8自由度飛行動力學模型。通過算例將所建模型與仿真結果進行對比,驗證了所建模型能夠精確、完整地描述多體飛行器空間運動的位形。

2)基于所建模型對組合式三體飛行器的配平狀態進行了求解及分析。在給定配平方案后,相較于常規飛行器在同一速度或迎角下只有一個配平點,該飛行器在給定飛行速度和迎角時存在兩個配平點,分別為“對稱下反”配平點1和“對稱下反”配平點2;飛行器在“對稱下反”配平狀態的相對滾轉運動具有靜穩定性,在“對稱上反”配平狀態的相對滾轉運動靜不穩定。此類多體飛行器在配平時不僅要考慮縱向力和力矩平衡,還需保證橫側向受力平衡和相對滾轉力矩平衡,其剛體飛行力學縱向和橫側向的動力學方程不能解耦。

3)在兩個配平狀態下分別對飛行器系統進行動力學特性分析,組合式三體飛行器相較于常規飛行器多出4個新生運動模態。4個新生運動模態按運動特性可劃分為復合對稱運動和復合反對稱運動兩類。組合式三體飛行器表現出雙機組合形式不具備的復合反對稱運動模態,可以更加全面地反映此類組合式飛行器的飛行力學特性信息。

4)在“對稱下反”配平點1處,飛行器的復合對稱運動模態和復合反對稱運動模態均收斂,但螺旋模態發散,倍幅時較短。在“對稱上反”配平點2處,飛行器的傳統飛行力學模態均收斂,但復合對稱運動模態和復合反對稱運動模態各存在1個發散的特征根,且倍幅時很短,無控狀態下影響飛行器穩定性。“對稱上反”狀態增強了整個飛行器的機翼上反效應,改善了螺旋模態特性。

5)基于串級PID控制器設計方法,設計了組合式三體飛行器的增穩控制系統。姿態增穩控制設計主要針對滾轉角φa和兩個相對滾轉角φba、φca進行。利用姿態角速度作為內環比例積分控制器的反饋量,利用姿態角作為外環比例控制器的反饋量,控制輸出為副翼舵偏指令。經過仿真分析,該增穩控制方案合理有效,可以快速鎮定發散的飛行力學系統。

針對組合式飛行器的多體動力學建模方法和增穩控制系統設計方法移植性較強,可為同類多體飛行器的設計分析提供指導與參考,且本文的建模方法直接對相對運動狀態量進行解算,十分方便飛行控制系統設計。對于此類多體飛行器的研究設計,本文作出如下展望:研究不同連接剛度對整個多體飛行器動力學特性的影響;研究此類飛行器受到環境、大展弦比、柔性變形等因素影響下的智能控制技術等。