一種單級控制的高精度指向系統研究

杜永剛, 王雪松, 王禺林

(中國空間技術研究院 蘭州空間技術物理研究所, 甘肅 蘭州 730000)

0 引言

高精度指向系統被廣泛應用在航天、航空領域,是該領域內的關鍵技術。在航天、航空領域,各種光學系統對其指向提出了極高的要求,如美國的詹姆斯·韋伯望遠鏡要求其指向系統的精度達到0.007″[1],美國論證中的大型紫外-可見光-紅外綜合天文望遠鏡要求其指向系統的精度不低于0.000 34″[2]。近期中國研制的小衛星“凝視”熱成像儀以及中國首顆太陽專用觀測衛星的X射線成像儀都對其指向系統的精度提出了極高的要求[3-4],中國的“墨子”號量子衛星的指向系統的精度達到0.000 4″[5]。光電跟瞄設備是航空戰斗機吊艙系統的核心組成,其指向系統的精度達到了亞微弧度的精度,如某機載激光通訊吊艙采用了一種復合指向系統,其指向精度可達0.002″[6],高精度指向系統也是航母艦載機著艦引導光電設備的關鍵組成[7]。

近年來光通訊技術發展迅猛,該領域也對高精度指向技術表現出強烈的需求態勢,如現代民用無人機的集群控制采用了激光通訊,它的核心組成之一就是高精度指向系統[8],它也是水下激光通信系統的核心組成[9]。高精度指向系統的研究依然具有重要的意義和價值。

目前,采用壓電陶瓷致動器的指向系統可以實現單級控制的高精度指向的性能[10-12],但是這種指向系統的工作空間極小[13-14],限制了其應用,所以現在的高精度指向系統采用了雙級控制技術,即采用一級機構穩定加上快速反射鏡二級穩定的粗精雙穩定系統,這種雙級系統具有較高的技術復雜性,因此單級控制的高精度指向系統受到了廣泛關注。李仕華等[15]優化了一種球面5R指向機構,提高了其工作空間和靈巧性。田少乾[16]提出一種新型的3-RRCPR并聯指向機構,通過改進控制算法使其角位移誤差小于0.85°,其線位移誤差范圍是0.02～0.03 mm。白智龍等[17]提出一種單級串聯指向機構,其指向機構是萬向節結構,通過研究永磁同步電機的控制算法,使該指向系統的穩態指向精度達到了1″。王玫羽等[18]提出了一種新型串聯球面指向機構,其應用對象是機載光電平臺,實現載荷在俯仰、方位及橫滾的三軸調整,其測試的指向誤差不大于0.25°。殷康程等[19]研究了一種星載雙反射天線的指向機構,該指向機構將雙軸間的連桿作為支撐和運動傳遞組件,具有運動范圍廣、結構緊湊、體積小、重量輕等特點,其雙軸的工作空間分別為0～163°和0～360°,其指向精度優于0.03°。趙穎等[20]研究了一種衛星天線的指向機構,這種指向機構是電機驅動的一個單自由度關節,其單軸精度可以達到0.008°。楊鵬等[21]則報道了一種應用于空間光學跟蹤系統的高精度二維指向機構,它承受的光學載荷質量約為100 kg,指向精度優于0.014°。

隨著空天地海一體化的軍事發展技術需求,空間立體化作戰系統對其天地通訊技術提出了更高的要求,要求某指向系統具有小體積、大承載以及高精度的性能指標,同時要求低成本,因此不能采用復雜和高成本的雙級控制指向系統,在這種背景下,本文提出一種單級控制的高精度指向系統,并通過理論計算和實驗驗證的方法對其進行了研究,詳細闡述了這種單級控制的高精度指向系統的工作原理、理論模型、模擬仿真與實驗測試,研究成果為后續工程應用奠定了基礎。

1 指向系統組成及原理

1.1 組成

圖1為這種單級控制的高精度指向系統的組成,其主要構成為傳動機構、控制器以及上位計算機。該指向系統通過消除傳動環節的位置浮動實現高指向精度的性能,其技術指標是:單軸誤差不大于0.005°,空間合成誤差不大于0.008°,載荷不小于100 kg。

圖1 高精度指向系統的組成結構

考慮到工程應用,該指向系統采用了嵌入式控制技術,控制器的軟件由C語言編寫,指向指令由一臺上位計算機模擬并給出。上位計算機為下位控制器給出指向命令,下位控制器按照指令解算出執行機構的執行參數,即兩個分支的輸出位移,而位置傳感器則把指向位置反饋給控制器,根據誤差消除算法,控制器會對實際的指向位置進行修正直至達到目標精度。

1.2 傳動及控制原理

圖2 并聯機構的組成

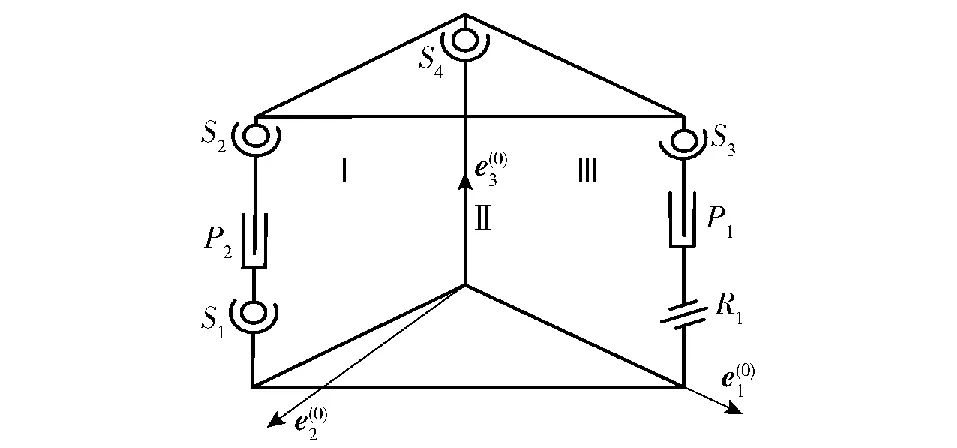
圖3 機構原理圖

對于空間機構的自由度計算方法已提出多種觀點,普遍認可的方法是轉換空間機構為平面內的解算關系[23-24]。式(1)被用來計算這種并聯機構的自由度:

W=Px-λ-3N

(1)

式中:W是空間機構的自由度數目;Px是空間機構運動副的自由度總數;λ是空間機構運動副的多余自由度數目;N是空間機構的封閉環數。本文設計的指向機構有3個封閉環,分別是環Ⅰ、Ⅱ、Ⅲ,封閉環的位置見圖3。對于環Ⅰ,其自由度為WⅠ=10-6-3×1=1;對于環Ⅱ,其自由度數WⅡ=12-8-3×1=1;對于環Ⅲ,其自由度數為WⅢ=8-5-3×1=0。因此整個指向機構的自由度數為W=WⅠ+WⅡ+WⅢ=2,表明指向機構的自由度符合了設計。

綜合誤差是導致并聯機構精度損失的主要原因[25-26],設計合理的控制策略可有效降低并聯機構的精度損失。基于RPS-SPS并聯機構,本文開發了誤差消除算法,形成以消除誤差為核心目標的控制策略,該控制策略如圖4所示。上位計算機給出預期指向矢量nexp,該指向矢量由一個控制器完成解算,控制器解算后得到兩個分支的矢量值pexp,控制器根據該值調整兩個分支,一個超高精度的位置傳感器測量實際位置,并被表示為矢量ntrue,指向誤差是矢量ntrue和nexp之間的差異,并被定義為μerror=‖ntrue-nexp‖。如指向誤差大于0.005°,控制器繼續調整機構,當指向誤差小于0.005°,指向機構則停止調整,過程調整量由誤差消除算法解算并給出。

圖4 指向機構的控制策略

鉸鏈間隙會導致傳動誤差[27-28],本文利用一種新型滾動球軸承消除球鉸的配合間隙誤差。這種軸承通過滾子的過盈配合消除了運動間隙,同時該球軸承的結構進一步簡化了誤差消除算法。圖5是這種滾動球軸承的外形。

圖5 指向機構的滾動球軸承

本文提出一種雙模型比較的誤差消除算法,其原理是建立一個標準模型,該標準模型作為標準對機構實際輸出位置進行誤差校驗。設定控制誤差帶為μerror≤0.005°,算法根據雙模型的誤差校驗數據計算出指向的調整量,控制器再根據調整量調整指向機構的分支矢量pcor,當指向誤差小于控制誤差帶后,指向機構停止位置指向,圖6為這種誤差消除算法的流程,流程圖說明運動學模型是由反向解算模型和正向解算模型組成。

圖6 指向機構的誤差消除算法流程

2 運動學模型及其仿真計算

2.1 運動學反解模型

圖7 空間坐標系的定義

圖8 單分支的矢量定義

根據空間幾何學和單分支的矢量定義,可得

(2)

(3)

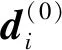
(4)

(5)

(6)

(7)

2.2 運動學正解模型

正向解算模型是從兩個分支矢量pi推出指向矢量n。圖9為兩個分支矢量的定義,定義從球鉸S3指向球鉸S2的矢量為f,其他矢量的定義同圖8。

圖9 雙分支的矢量定義

(8)

(9)

2.3 仿真計算

本文利用MATLAB軟件編寫上述模型的仿真程序,表1中列出了指向機構的參數。因參數b的精度難以保證,計算程序設定b的誤差范圍為5 mm,然后對這種跟蹤指向系統的工作空間和指向誤差等進行仿真計算。

表1 指向機構的參數

圖10為指向機構工作位置空間的計算結果。圖10中坐標軸是指向矢量n繞X、Y軸的工作角,云圖則表達了指向矢量n和Z軸夾角,從圖10中可得出該指向機構的工作空間為X、Y兩軸±9°。

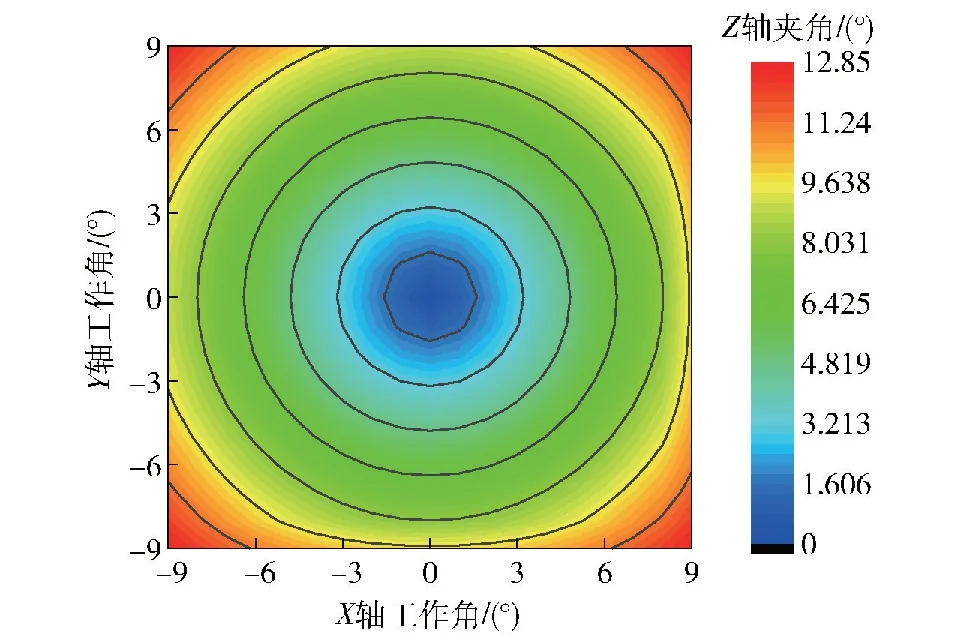
圖10 機構工作空間的仿真結果

指向誤差的仿真結果如圖11和圖12所示。圖11 中的數據表明該指向機構的理論單軸誤差不大于0.001 2°,圖12中可以得出其理論空間合成誤差不大于0.002°。

圖11 單軸誤差的仿真結果

圖12 合成指向誤差的仿真結果

3 實驗及分析

3.1 實驗

本文開發的原型機如圖13所示,并開展了實驗測試研究。原型機的參數選用表1中的數據。

圖13 系統原型機的外觀照片

首先測試了指向系統的工作空間。上位計算機給出兩軸每間隔3°的指向指令,位置傳感器獲得指向機構兩軸的角度位置數據,圖14為測試數據形成的位置點圖,從中可以得出該系統的工作空間滿足了兩軸±9°的要求。

圖14 工作空間的測試結果

其次,分別測試了空載和110 kg載荷下的單軸指向誤差,測試的結果如圖15所示,從中可以得出在兩種載荷條件下該系統的單軸指向誤差均不大于0.004°。同時,測試了指向系統的空間合成指向誤差,其測試結果如圖16所示,從中可知在兩種載荷條件下,該系統的空間合成指向誤差均不超過0.006°。

在研究新型城鎮化背景下我國城市精明增長與蔓延發展的關系時，不可割裂看待精明增長與城市蔓延，這兩者是城市發展過程中不可或缺的階段，有相互交織、相互依存的關系，對各地城市發展都有一定的意義。

圖15 單軸誤差的測試結果

圖16 合成誤差的測試結果

然后,本文中也驗證了雙模型比較誤差消除算法的有效性。設置指向誤差控制帶為0.005°,測試了X、Y兩軸分別間隔1°的位置比較次數,其測試的數據如圖17所示。測試結果表明:在兩種載荷條件下,誤差消除算法的比較次數均不超過3次。

圖17 比較次數的測試結果

最后,開展了指向系統的響應速度測試。響應速度是評價指向系統的重要指標,本文用指向穩定時間表征高精度指向系統的響應速度,指向系統的穩定時間越短,表示其響應速度越高。設定控制誤差帶為0.005°,并測試了原型機的指向穩定時間,圖18為測試的結果。實驗數據表明在兩軸±9°的工作空間內,原型機的指向穩定時間均小于100 ms。

圖18 穩定時間的測試結果

3.2 結果分析

本文旨在獲得一種單級控制的高精度指向系統,要求其建造成本低,同時具有小體積、大承載以及高精度的性能指標。兩個關鍵設計使本研究達到了預期目標,其一是該指向系統采用了一種2自由度的RPS-SRS并聯機構,這種新型的并聯機構利用中間球鉸副消除了位置浮動,同時也消除了載荷重量對傳動鏈的作用;其二是采用了基于RPS-SRS并聯機構的雙模型比較誤差消除算法,算法進一步改善了指向精度和穩定性。理論模型的仿真結果表明這種指向系統的工作空間可達到兩軸±9°,其單軸誤差不大于0.001 2°,其合成誤差不大于0.002°。

為進一步證實這種設計思想的正確性,本文開展了原型機的實驗研究,原型機采用和理論模型相同的機構參數,其測試結果證明指向系統的工作空間可達兩軸±9°,單軸誤差不大于0.004°,其空間合成誤差不大于0.006°,其可承受的載荷不小于110 kg。理論和實驗研究的結果均證實了這種指向系統的可行性和有效性。研究結果也表明這種單級控制的高精度指向系統存在以下特點:

1) 非對稱性。指向系統具有兩個不同的分支形式,因此理論仿真和實驗誤差數據均出現不對稱形態,這種不對稱的形態如圖11、圖12、圖15和圖16 所示。但機構的工作空間是對稱的形態,圖19 為該系統空間坐標系中的指向位置,因此這種非對稱性并不影響指向系統的功能。

圖19 空間坐標系中的指向位置

2) 指向精度表現出對慣量的敏感性。RPS-SPS并聯機構通過中間球鉸副消除了載荷重量對分支的作用,這使載荷慣量成為影響精度的主要因素之一。載荷慣量和其質量成正比關系,因此原型機在加載狀態下的指向誤差大于空載下的數值。通過對比圖11 和圖15、圖12和圖16,可以得出以下結果:仿真的指向誤差小于空載的誤差,而空載的誤差又小于加載的誤差,理論計算和實驗數據均證實了這個特點,因此減少載荷質心到中心球鉸的距離能有效提高指向精度。

3) 指向精度表現出對振動的敏感性。當原型機周圍存在振動擾動時,測試的誤差也明顯增大,研究也表明振動環境能對指向精度產生嚴重擾動[31],這也是測試數據比仿真結果表現出更大離散性的原因之一。

4) 指向穩定時間表現出對載荷不敏感的特性。在兩種載荷狀態下,大部分位置點的穩定時間都小于30 ms,只有少數位置點的穩定時間接近于100 ms。 圖18表明空載和加載狀態下的實驗數據基本一致,這說明雙模型比較誤差消除算法起到了作用。

綜合以上的分析,本文提出的這種高精度指向機構在大載荷下依然有很好的響應特性,這得益于其穩定時間對載荷不敏感的特點,但需要考慮載荷慣量對指向精度的影響,通過降低載荷質心位置減少了該影響,最終的技術方案匹配了某系統的功能要求,也滿足了大載荷、高精度的性能指標。

4 結論

基于消除指向機構的位置浮動環節可提高指向精度的原理,本文研究了一種單級控制的高精度指向系統,可實現大負載、高精度的指向性能。得出以下主要結論:

1) 指向系統原型機在110 kg的載荷下,其達到的性能指標為:單軸誤差≯0.004°,空間合成誤差≯0.006°,指向穩定時間≯100 ms,工作空間為兩軸±9°。

2) 消除并聯機構的中間位置浮動環節可有效提高指向精度。研究的指向系統采用了一種無中間位置浮動環節的RPS-SRS并聯指向機構以及雙模型比較法的誤差消除算法,其理論和實驗結果均驗證了該設計思想的正確和有效性。

3) 原型機的實驗結果表明振動環境會對指向造成擾動,振動抑制能改善原型機的指向精度。RPS-SRS并聯指向機構及其信號處理系統中的振動抑制技術成為研制工程樣機的重要環節。