大型梁式反力系統的結構力學特性研究

黃 鋒,張 班,劉星辰,楊正旭,屈苗迪

(1. 重慶交通大學 山區橋梁與隧道工程國家重點實驗室,重慶 400074; 2. 重慶交通大學 土木工程學院,重慶 400074; 3. 河南省交通規劃設計研究院股份有限公司,河南 鄭州 451450)

0 引 言

在實驗室中,部分模型試驗需要大噸位的加載系統,如高地應力隧道縮尺模型試驗、足尺模型試驗,這類大噸位的加載問題是實驗室的重難點之一。加載系統一般由反力架、反力墻、反力梁等組成,并安裝加載裝置,實現對荷載的精確控制。

為了滿足自身試驗的加載要求,學者們對反力系統進行了設計和研究。涂熙等[1]設計了1 296 t噸位的反力體系,通過有限元和試驗分析,驗證了剛度滿足試驗要求;晁曉艷等[2]自行設計了反力架,但加載噸位較小;柴振嶺[3]采用有限元數值模擬與理論分析相結合的方法,研制了一種適用于教學與科研的拉壓雙作用梁式反力架,但無法實現大噸位荷載試驗;王輝等[4]通過試驗和有限元分析了大噸位反力梁的應力和變形,提出設計時應對螺栓孔附近進行加固,但并未研究極限荷載下的反力梁力學特性。

大噸位工況下,由于反力梁及連接節點結構剛度不足,在加載過程中會導致反力梁與試驗對象產生整體相對位移及較大的撓度變形[5]。為實現加載裝置對荷載的精致控制,需對反力系統進行結構強度分析。

目前,對結構強度的研究主要包括試驗研究和有限元分析。周智海等[6]采用有限元分析,對高架橋影響軌道線路區間的最不利斷面,進行了軌道結構位移與變形等相關安全影響的計算分析,研究了擬建市政道路高架橋對既有軌道結構的安全影響;楊敬東等[7]對絞車作業中4種工況的結構進行有限元強度校核,驗證了絞車支撐結構加強方案合理可行。試驗研究能直觀準確獲取結構的力學特性[8-9],但有些試驗設計和實施條件要求高、控制嚴、難度大,在實際工作中有時難以做到。有限元分析應用廣泛,但在本構模型選取、材料參數確定等方面存在較大困難,導致研究成果在指導實際工程時具有一定局限性[10]。將試驗和有限元結合,在兩者結果吻合較好的基礎之上,再分析結構的受力特性[11]。

針對重慶交通大學隧道實驗室地下結構三維加載試驗平臺的設計思路和結構特點,通過靜載試驗和有限元分析,對反力梁和螺栓進行強度驗證和變形研究。同時,深入探索了極限荷載下的反力梁和螺栓的力學特性,為后續梁式反力系統的建設者提供良好的經驗。

1 反力系統設計

重慶交通大學隧道實驗室地下結構三維加載試驗平臺,其加載能力16 500 kN(1 684 t),底部采用高強度鋼筋混凝土,側面為高強度鋼筋混凝土反力墻,頂部為大型鋼結構反力梁,如圖1。

圖1 反力系統Fig. 1 Reaction system

1.1 設計思路

在反力墻的臺座上,設有圖2(a)所示的地腳螺栓孔,通過螺栓將反力梁與反力墻固定,組成反力系統,反力梁尺寸如圖2(b)。

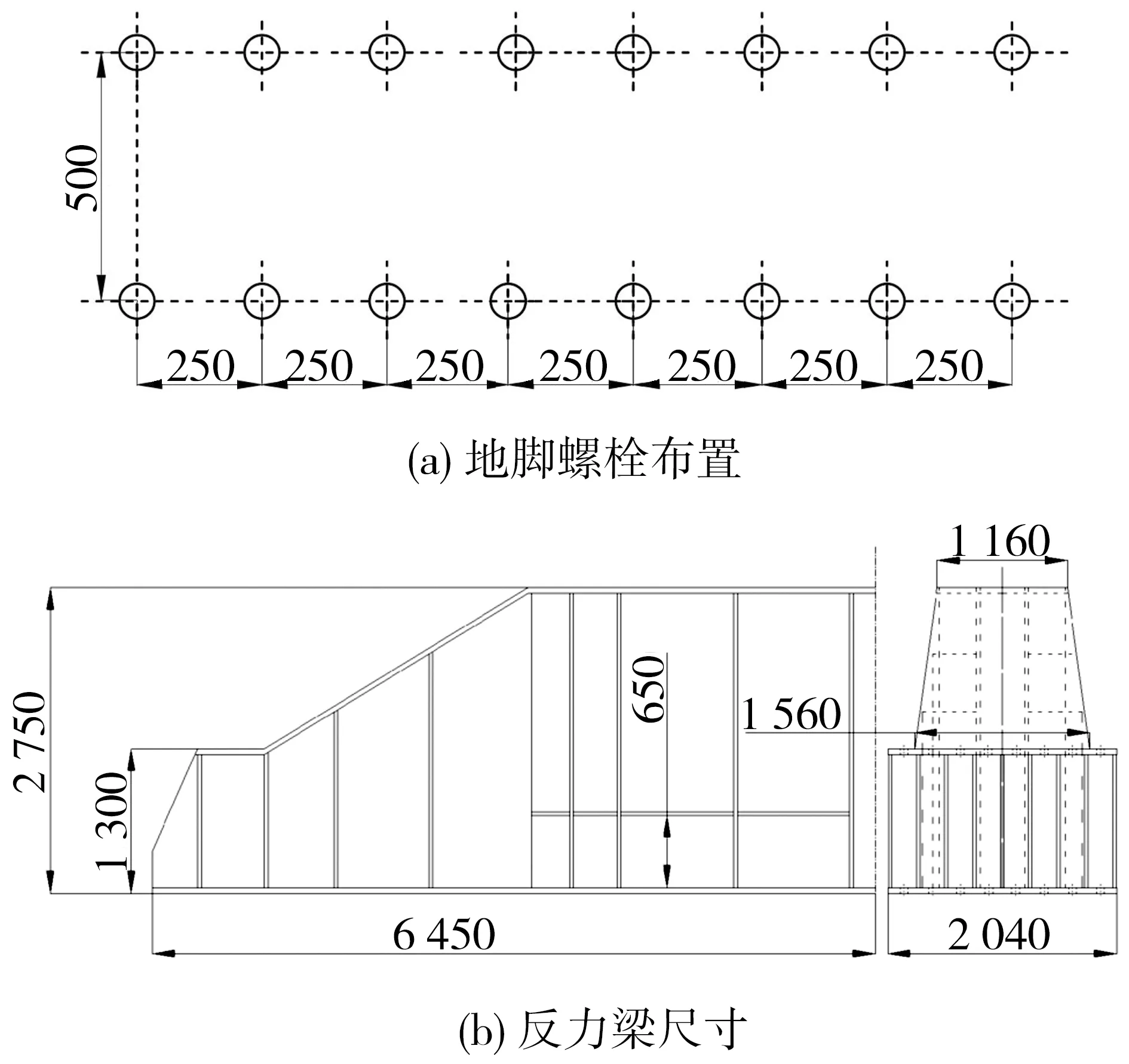
圖2 設計圖(單位:mm)Fig. 2 Design drawing

1.2 設計原則

1)底部采用的高強度鋼筋混凝土、側面的反力墻、頂部的大型鋼結構反力梁以及螺栓連接節點處的剛度足夠大,滿足最大荷載量(1 684 t)的要求,同時要滿足12%的安全儲備。

2)反力系統自身的變形量,尤其是反力梁的變形量,要符合試驗要求(反力梁長度的1/1 000)。

3)反力梁的結構簡單,重量輕,方便吊裝。

1.3 結構與特點

考慮結構組合效應,確定反力梁的結構形式,反力梁與反力墻通過螺栓連接,如圖1。反力梁總長為12 900 mm,主體采用Q345B級鋼板焊接而成,重44.75 t,連接螺栓采用40Cr鋼,螺栓桿直徑70 mm。平臺最大加載1 684 t,可突破高地應力隧道縮尺模型試驗的加載瓶頸,滿足試驗加載要求。

2 反力系統力學特性分析

反力系統的底部和側面反力墻采用高強度鋼筋混凝土澆筑而成,剛度足夠大,滿足最大荷載(1 684 t)下的變形要求,所以主要研究反力系統中鋼結構反力梁和螺栓連接節點的力學特性。

2.1 有限元分析

采用有限元軟件ABAQUS對反力系統進行分析,通過緣、腹板、隔板、支座端板、加勁肋板裝配組成反力梁,不考慮焊接差異[12],材料使用Q345鋼進行模擬。螺栓、螺母、剛性支座采用高強度鋼材料,有限元模型中,鋼材采用理想彈塑性模型,材料的力學性能見表1。

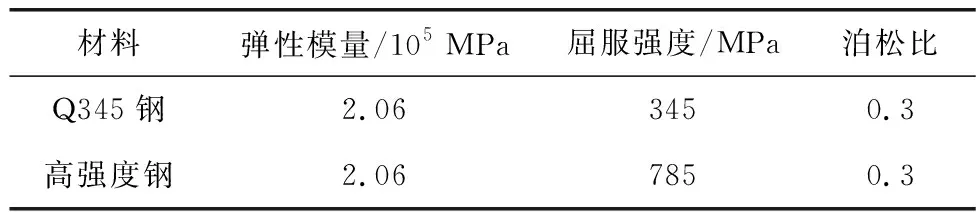
表1 鋼材的力學性能Table 1 Mechanical properties of steel

圖3(a)中底座的邊界條件采用全約束,螺栓、螺母、支座和反力梁之間的接觸面采用硬接觸[13],根據GB 50017—2017《鋼結構設計規范》,摩擦系數設置為0.15。考慮模型自重,采用3點加載,單點加載力為5 500 kN,加載位置如圖3(b),加載區域由圓柱體和長方體組成,荷載加在圓柱體上,同時約束長方體x、z方形的位移,確保內部圓柱體在加載過程中沿y方向移動。模型結點總數225 852個,單元采用C3D8(8結點線性6面體),總數148 707個。

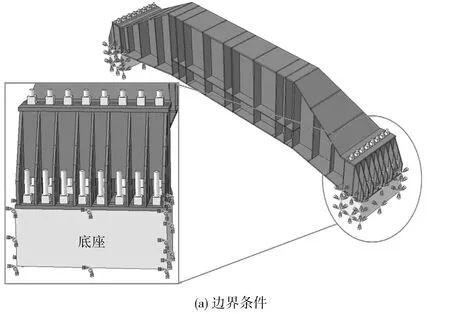
圖3 有限元模型Fig. 3 Finite element model

反力系統構件的應力云如圖4。圖4表明:反力梁在螺栓孔區域發生應力集中,最大應力345 MPa,反力梁強度滿足試驗要求;螺栓最大應力551 MPa,螺栓強度滿足試驗要求。

圖4 反力系統構件的應力云圖Fig. 4 Stress nephogram of reaction system components

通過有限元分析,反力梁的豎向位移變形(放大100倍)如圖5。反力梁上翼緣板的位移整體小于下翼緣板,表明上、下翼緣板之間的鋼板存在壓縮現象,下翼緣板的位移更能代表試驗真實位移。

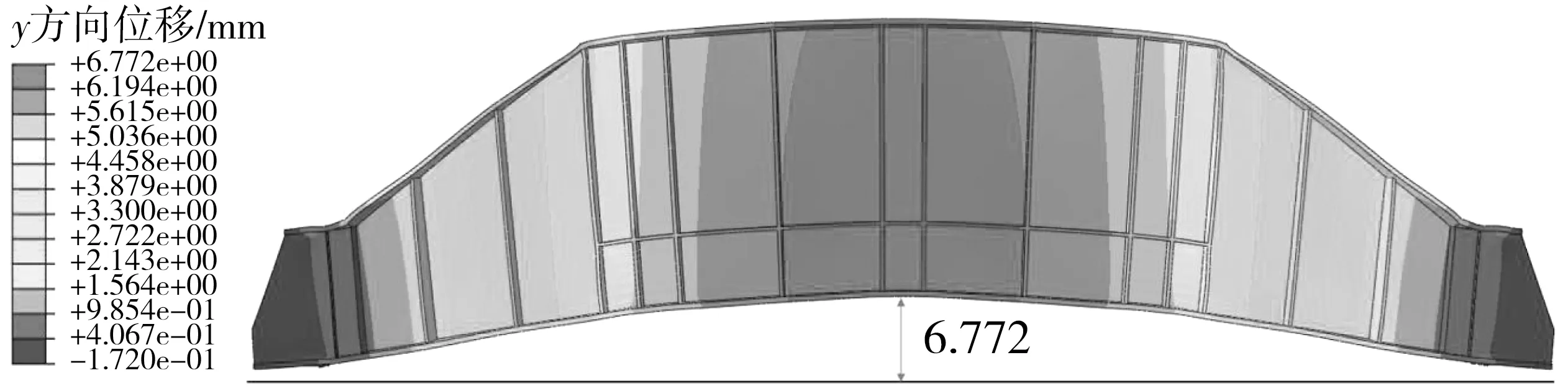
圖5 反力系統y方向的位移云圖(單位:mm)Fig. 5 Displacement nephogram of reaction system in the y direction

將螺栓支座沿x方向(反力梁軸線方向)的位移變形放大500倍,如圖6。螺栓在螺母連接處,向反力梁方向發生內凹,最大位移0.550 mm。在內排螺栓頂部,發生遠離反力梁方向的位移,最大變形值1.138 mm。

圖6 x方向螺栓位移變形云圖Fig. 6 Nephogram of bolt displacement and deformation in x direction

變形后的螺栓簡圖如圖7,根據三角形公式,計算出螺栓變形角度α=0.3°,β=0.069°,表明螺栓節點屬于半剛性結構。

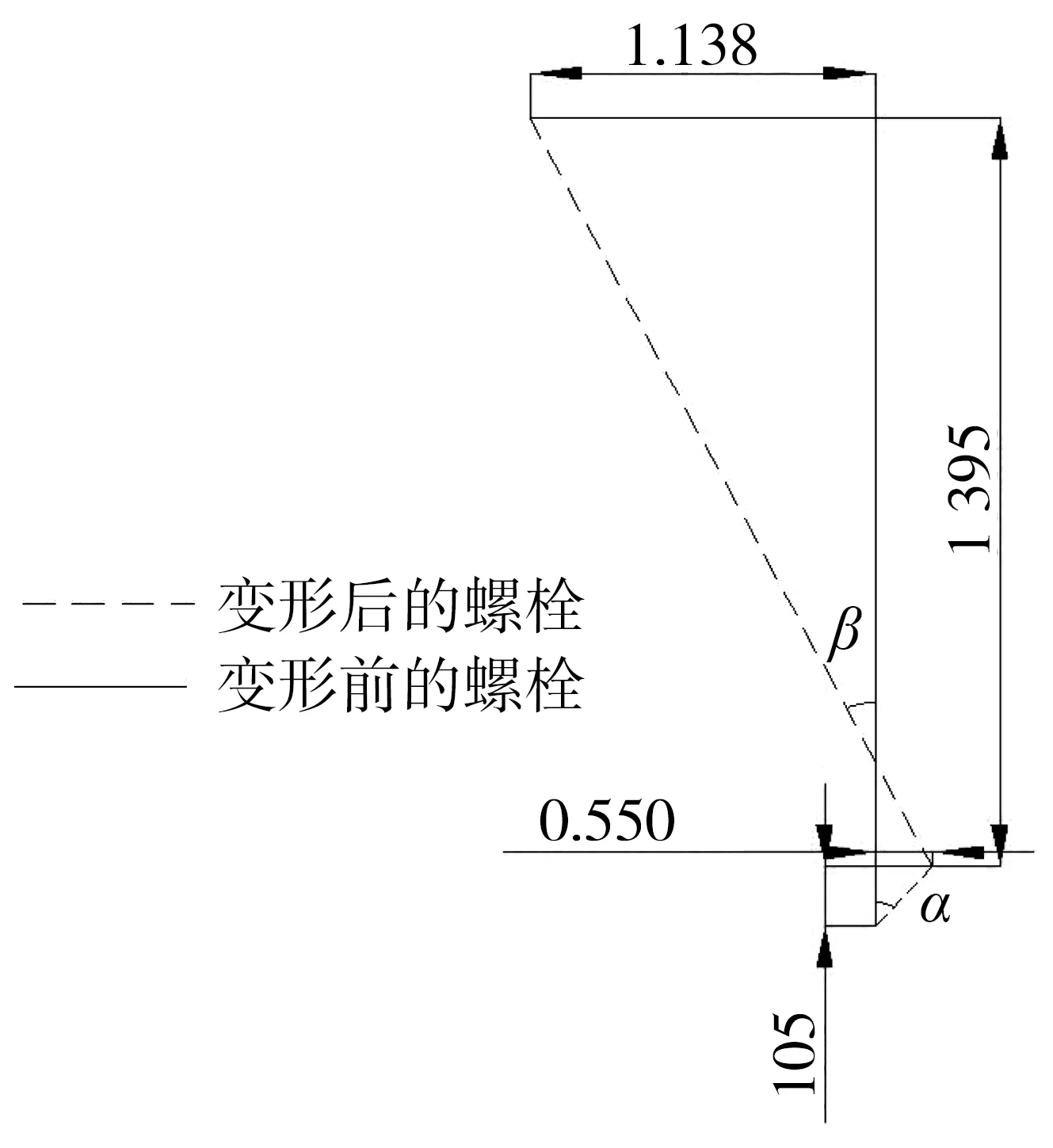
圖7 x方向螺栓位移變形簡圖(單位:mm)Fig. 7 Displacement and deformation diagram of bolt in X direction

選取一個內排螺栓,繪制其荷載-轉角曲線,如圖8。螺栓轉角隨荷載增加幾乎呈直線增加,通過計算荷載和轉角曲線的斜率發現,斜率隨荷載的增加由3.17×10-5增加到3.74×10-5,增加了18%。

圖8 荷載-轉角曲線Fig. 8 Load-rotation angle curve

2.2 試驗分析

反力系統單點最大設計荷載5 500 kN,頂部設置3個荷載加載點,3點同時加載,共計16 500 kN,集中荷載的作用點如圖9。

圖9 測點分布(單位:mm)Fig. 9 Distribution of measuring points

試驗主要監測梁的豎向位移和應變。位移計布置在上翼緣板的兩端、跨中和加載點的正上方,記為①～⑤,位置如圖9。測點1～7用于監測梁上翼緣的應變,測點8～15用于監測梁下翼緣的應變,測點16～21用于監測梁中前鋼板的應變,位置如圖9。

為了測量最大設計荷載作用下反力梁的位移和應變等力學特性,試驗先預加載、正常荷載加載,最后采用分級加載方案:以500 kN為步長,從0開始,共11步,3點同時加載,直到5 500 kN,停止加載。

通過試驗測點應變數據,利用公式(1),獲得試驗測點應力,得到的荷載-應力曲線如圖10。

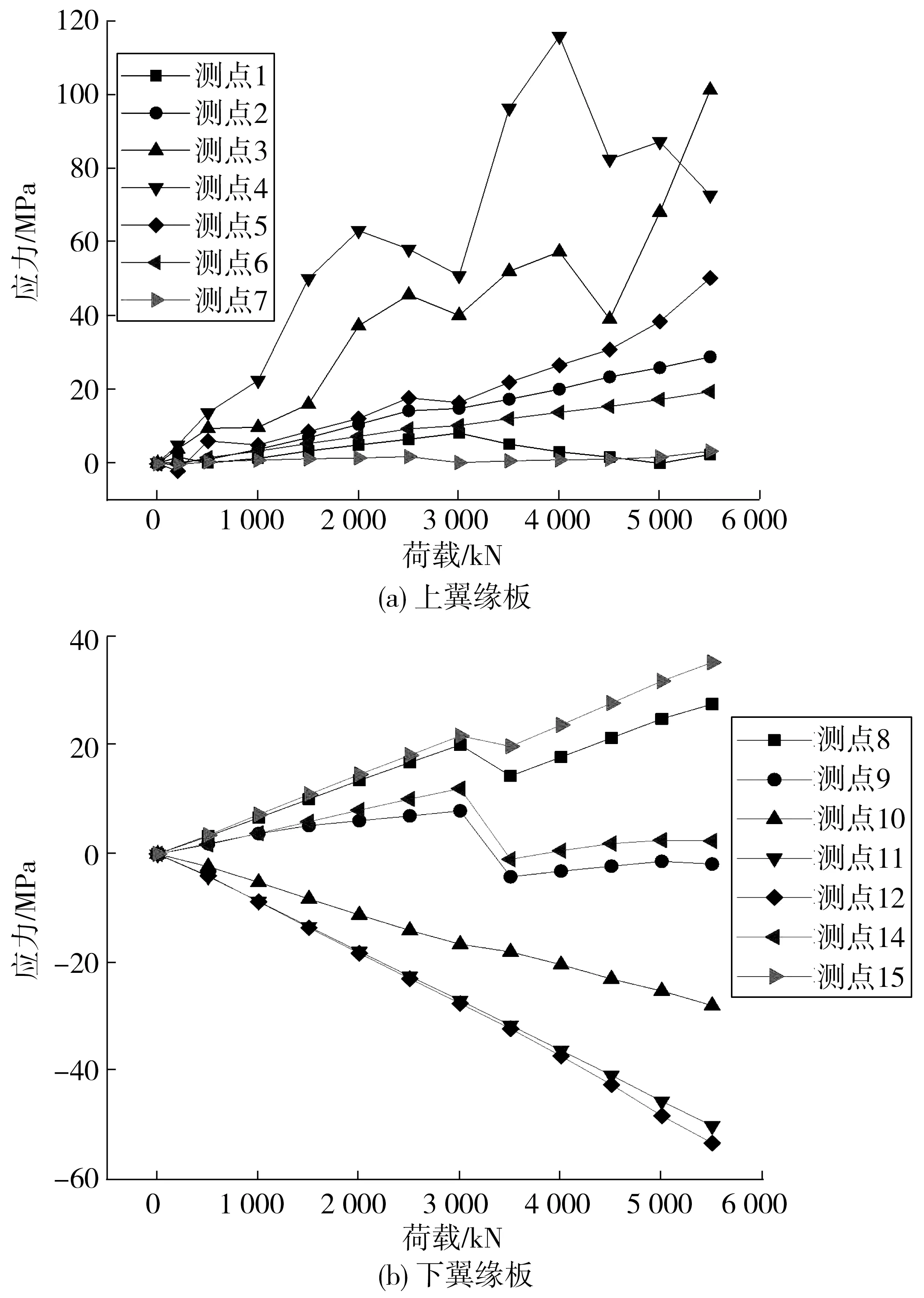
圖10 荷載-應力曲線Fig. 10 Load-stress curve

(1)

式中:εx為x方向的應變;σx為x方向的應力;E為彈性模量。

由圖10可知:在加載過程中,上翼緣板測點的應力為正值,表明上翼緣板處于受拉區;下翼緣板測點8、15應力為正值,表明其位于受拉區,測點10、11、12應力為負值,表明其處于受壓區,測點13測試中損壞,無讀數,測點9、14的應力值在3 000～3 500 kN荷載區間,由正值突變為負值,表明其位置由受拉區變為受壓區,原因可能是螺栓節點處的螺栓發生了滑移。荷載在2 500～3 000 kN區間,上翼緣板測點3、4、5的應力值出現了不同程度的降低,之后應力又繼續上升;荷載在4 000～5 000 kN區間,上翼緣板測點3、4的應力出現了先減小后增大的現象;荷載在3 000～4 000 kN區間,下翼緣板測點8、15的應力再次出現了先減小后增大的現象。表明螺栓節點處螺栓可能發生了滑移,導致應力突然減小,出現了應力釋放的現象,螺栓穩定后,測點應力繼續增大。

加載引起的荷載-位移曲線如圖11。①和⑤處測得的最大位移為1.69 mm和1.17 mm,表明螺栓連接的剛度不足,反力梁出現向上的整體位移。③位于梁中點,加載過程中,豎向位移最大,最大位移變形量10.91 mm。根據①和⑤處的位移,測得梁中點的實際撓度為9.48 mm,小于梁的要求變形量12.90 mm(梁長度的1/1 000)。

圖11 荷載-位移曲線Fig. 11 Load-displacement curve

2.3 結果對比分析

為了驗證有限元結果的準確性,將試驗結果和有限元結果進行對比分析。

選取上翼緣板的測點1～4,進行應力對比分析。試驗測點應力圍繞有限元測點應力上下浮動,如圖12,表明了有限元模型的準確性,圖中FE、T分別為該點的有限元結果、試驗結果。

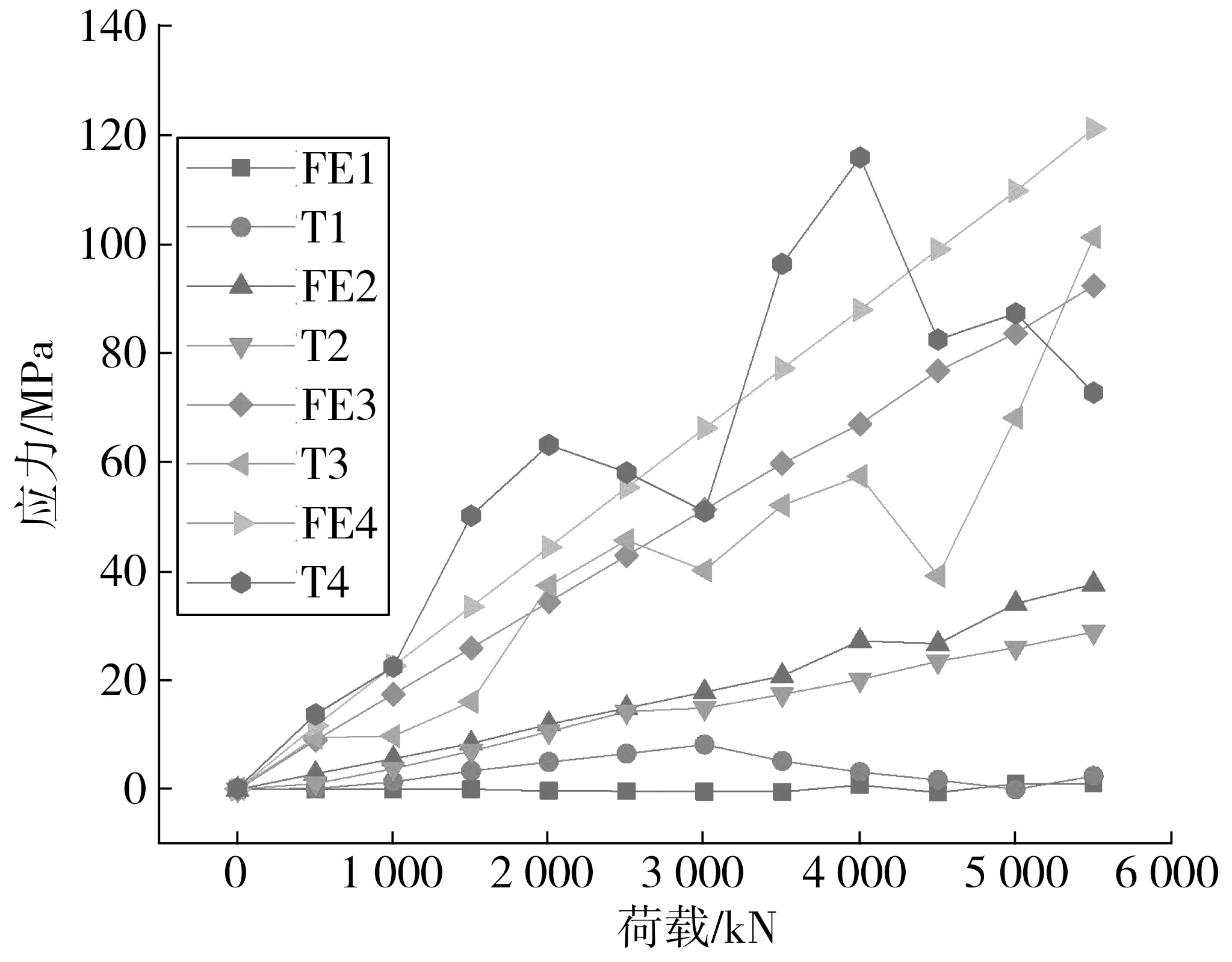
圖12 荷載-應力曲線Fig. 12 Load-stress curve

3 失穩下的力學特性分析

為研究反力梁在失穩下的力學特性,首先通過試驗數據驗證了有限元分析的準確性,然后采用有限元模型模擬失穩下反力梁的破壞變形規律。采用遠大于極限荷載的力對反力系統進行加載,獲取反力梁失穩的位移變形如圖13(放大15倍)。

圖13 反力梁位移變形Fig. 13 Displacement deformation of reaction beam

豎向肋板在底部產生了較大的水平變形,最大位移20.40 mm;水平肋板在中部產生了較大的豎向變形,最大位移64.97 mm;腹板在兩端和底部產生了較大的z方向(垂直于腹板方向)變形,最大位移18.1 mm,具體位置如圖13。

將螺栓極限荷載下的位移變形放大15倍,如圖14。水平方向最大位移變形12.22 mm,豎向最大位移變形4.64 mm,z方向最大位移變形9.97 mm,具體位置如圖14。

圖14 螺栓位移變形Fig. 14 Displacement deformation of bolt

由圖14可知:反力系統在設計中,需要加強反力梁豎向肋板底部、水平肋板中部、腹板的兩端和底部處的剛度,以及螺栓水平方向的剛度,以提高反力系統的安全性和有效性。

4 結 論

通過對反力梁和螺栓節點的力學特性分析,發現螺栓節點底部的應力較大,在設計反力系統時,應加強對螺栓節點底部的反力梁剛度。同時,得到了如下結論:

1)通過試驗位移數據和有限元分析,驗證了反力梁的撓度變形滿足試驗要求。

2)根據加載后螺栓角度的變形分析,表明螺栓節點屬于半剛性結構,同時螺栓轉角隨荷載增大呈直線增加趨勢。

3)試驗測點應力存在先減少后增大的現象,可能是螺栓節點處螺栓發生了滑移。

4)在超過極限荷載時,反力梁的豎向肋板底部、水平肋板中部、腹板的兩端和底部,以及螺栓水平方向均發生了較大的位移變形,需增加這部分梁的截面慣性矩和螺栓水平方向的剛度,以確保反力系統的安全性和有效性。